【信号与系统 - 9】傅里叶变换的性质习题
1 习题
已知 f ( t ) f(t) f(t) 的傅里叶变换为 F ( j w ) F(jw) F(jw) ,求如下信号的傅里叶变换
-
(1) t ⋅ f ( 3 t ) t\cdot f(3t) t⋅f(3t)
解:
f ( 3 t ) ↔ 1 3 F ( j w 3 ) f(3t)\leftrightarrow \frac{1}{3}F(j\frac{w}{3}) f(3t)↔31F(j3w)
t ⋅ f ( 3 t ) ↔ j 1 3 ⋅ d d w [ F ( j w 3 ) ] t\cdot f(3t)\leftrightarrow j\frac{1}{3}\cdot\frac{d}{dw}[F(j\frac{w}{3})] t⋅f(3t)↔j31⋅dwd[F(j3w)]
其中: d ( w 3 ) = 1 3 d w d(\frac{w}{3})=\frac{1}{3}dw d(3w)=31dw,则 d w = 3 d ( w 3 ) dw=3d(\frac{w}{3}) dw=3d(3w),所以 d d w [ F ( j w 3 ) ] = 1 3 d d ( w 3 ) [ F ( j w 3 ) ] \frac{d}{dw}[F(j\frac{w}{3})]=\frac{1}{3}\frac{d}{d(\frac{w}{3})}[F(j\frac{w}{3})] dwd[F(j3w)]=31d(3w)d[F(j3w)],则 t ⋅ f ( 3 t ) ↔ j 1 9 ⋅ F ′ ( j w 3 ) t\cdot f(3t)\leftrightarrow j\frac{1}{9}\cdot F'(j\frac{w}{3}) t⋅f(3t)↔j91⋅F′(j3w) -
(2) ( t − 1 ) d [ f ( t ) ] d t (t-1)\frac{d[f(t)]}{dt} (t−1)dtd[f(t)]
解:
d [ f ( t ) ] d t ↔ j w F ( j w ) \frac{d[f(t)]}{dt}\leftrightarrow jwF(jw) dtd[f(t)]↔jwF(jw)
t ⋅ d [ f ( t ) ] d t ↔ j d d w [ j w F ( j w ) ] = − d d w [ w F ( j w ) ] = − [ F ( j w ) + w F ′ ( j w ) ] t\cdot\frac{d[f(t)]}{dt}\leftrightarrow j\frac{d}{dw}[jwF(jw)]=-\frac{d}{dw}[wF(jw)]=-[F(jw)+wF'(jw)] t⋅dtd[f(t)]↔jdwd[jwF(jw)]=−dwd[wF(jw)]=−[F(jw)+wF′(jw)]
( t − 1 ) ⋅ d [ f ( t ) ] d t ↔ j d d w [ j w F ( j w ) ] = − d d w [ w F ( j w ) ] = − [ F ( j w ) + w F ′ ( j w ) ] − j F ′ ( j w ) = − [ F ( j w ) + ( w + 1 ) F ′ ( j w ) ] (t-1)\cdot\frac{d[f(t)]}{dt}\leftrightarrow j\frac{d}{dw}[jwF(jw)]=-\frac{d}{dw}[wF(jw)]=-[F(jw)+wF'(jw)]-jF'(jw)=-[F(jw)+(w+1)F'(jw)] (t−1)⋅dtd[f(t)]↔jdwd[jwF(jw)]=−dwd[wF(jw)]=−[F(jw)+wF′(jw)]−jF′(jw)=−[F(jw)+(w+1)F′(jw)]
- (3) ( 2 − t ) f ( 2 − t ) (2-t)f(2-t) (2−t)f(2−t)
解:
f ( 2 − t ) = f [ − ( t − 2 ) ] ↔ F ( − j w ) e − j 2 w f(2-t)=f[-(t-2)]\leftrightarrow F(-jw)e^{-j2w} f(2−t)=f[−(t−2)]↔F(−jw)e−j2w
t ⋅ f ( 2 − t ) ↔ j d d w [ F ( − j w ) e − j 2 w = − j d d ( − w ) [ F ( − j w ) e − j 2 w ] = − j [ F ′ ( − j w ) e − j 2 w − j 2 F ( − j w ) e − j 2 w ] t\cdot f(2-t)\leftrightarrow j\frac{d}{dw}[F(-jw)e^{-j2w}=-j\frac{d}{d(-w)}[F(-jw)e^{-j2w}]=-j\Big[F'(-jw)e^{-j2w}-j2F(-jw)e^{-j2w}\Big] t⋅f(2−t)↔jdwd[F(−jw)e−j2w=−jd(−w)d[F(−jw)e−j2w]=−j[F′(−jw)e−j2w−j2F(−jw)e−j2w]
( 2 − t ) ⋅ f ( 2 − t ) ↔ 2 F ( − j w ) e − j 2 w + [ j F ′ ( − j w ) e − j 2 w − 2 F ( − j w ) e − j 2 w ] = j F ′ ( − j w ) e − j 2 w (2-t)\cdot f(2-t)\leftrightarrow 2F(-jw)e^{-j2w}+[jF'(-jw)e^{-j2w}-2F(-jw)e^{-j2w}]=jF'(-jw)e^{-j2w} (2−t)⋅f(2−t)↔2F(−jw)e−j2w+[jF′(−jw)e−j2w−2F(−jw)e−j2w]=jF′(−jw)e−j2w
2 补充:二倍角以及积化和差公式
{ c o s α ⋅ c o s β = 1 2 [ c o s ( α + β ) + c o s ( α − β ) ] 【调制】 s i n α ⋅ s i n β = 1 2 [ c o s ( α + β ) − c o s ( α − β ) ] c o s α ⋅ s i n β = 1 2 [ s i n ( α + β ) − s i n ( α − β ) ] s i n α ⋅ c o s β = 1 2 [ s i n ( α + β ) + s i n ( α − β ) ] \begin{cases} cos\alpha \cdot cos\beta=\frac{1}{2}[cos(\alpha+\beta)+cos(\alpha-\beta)]【调制】\\ sin\alpha \cdot sin\beta=\frac{1}{2}[cos(\alpha+\beta)-cos(\alpha-\beta)]\\ cos\alpha \cdot sin\beta=\frac{1}{2}[sin(\alpha+\beta)-sin(\alpha-\beta)]\\ sin\alpha \cdot cos\beta=\frac{1}{2}[sin(\alpha+\beta)+sin(\alpha-\beta)]\\ \end{cases} ⎩ ⎨ ⎧cosα⋅cosβ=21[cos(α+β)+cos(α−β)]【调制】sinα⋅sinβ=21[cos(α+β)−cos(α−β)]cosα⋅sinβ=21[sin(α+β)−sin(α−β)]sinα⋅cosβ=21[sin(α+β)+sin(α−β)]
s i n ( 2 α ) = 2 s i n α ⋅ c o s α sin(2\alpha)=2sin\alpha\cdot cos\alpha sin(2α)=2sinα⋅cosα
{ c o s ( 2 α ) = 2 c o s 2 α − 1 = 1 − 2 s i n 2 α = c o s 2 α − s i n 2 α c o s 2 α = c o s ( 2 α ) + 1 2 s i n 2 α = 1 − c o s ( 2 α ) 2 \begin{cases} cos(2\alpha)=2cos^2\alpha-1=1-2sin^2\alpha=cos^2\alpha-sin^2\alpha\\ cos^2\alpha=\frac{cos(2\alpha)+1}{2}\\ sin^2\alpha=\frac{1-cos(2\alpha)}{2}\\ \end{cases} ⎩ ⎨ ⎧cos(2α)=2cos2α−1=1−2sin2α=cos2α−sin2αcos2α=2cos(2α)+1sin2α=21−cos(2α)
t a n ( 2 α ) = 2 t a n α 1 − t a n 2 α tan(2\alpha)=\frac{2tan\alpha}{1-tan^2\alpha} tan(2α)=1−tan2α2tanα
相关文章:

【信号与系统 - 9】傅里叶变换的性质习题
1 习题 已知 f ( t ) f(t) f(t) 的傅里叶变换为 F ( j w ) F(jw) F(jw) ,求如下信号的傅里叶变换 (1) t ⋅ f ( 3 t ) t\cdot f(3t) t⋅f(3t) 解: f ( 3 t ) ↔ 1 3 F ( j w 3 ) f(3t)\leftrightarrow \frac{1}{3}F(j\frac{w}…...
:语法糖概念解析)
C#探索之路基础夯实篇(5):语法糖概念解析
C#探索之路基础夯实篇(5):语法糖概念解析 文章目录 C#探索之路基础夯实篇(5):语法糖概念解析1、概念定义2、Lua中的语法糖3、C#中的语法糖4、C中的语法糖5、优缺点辨析6、适用范围7、总结 从之前一开始接触lua的时候开始,开始第一次接触到语法…...
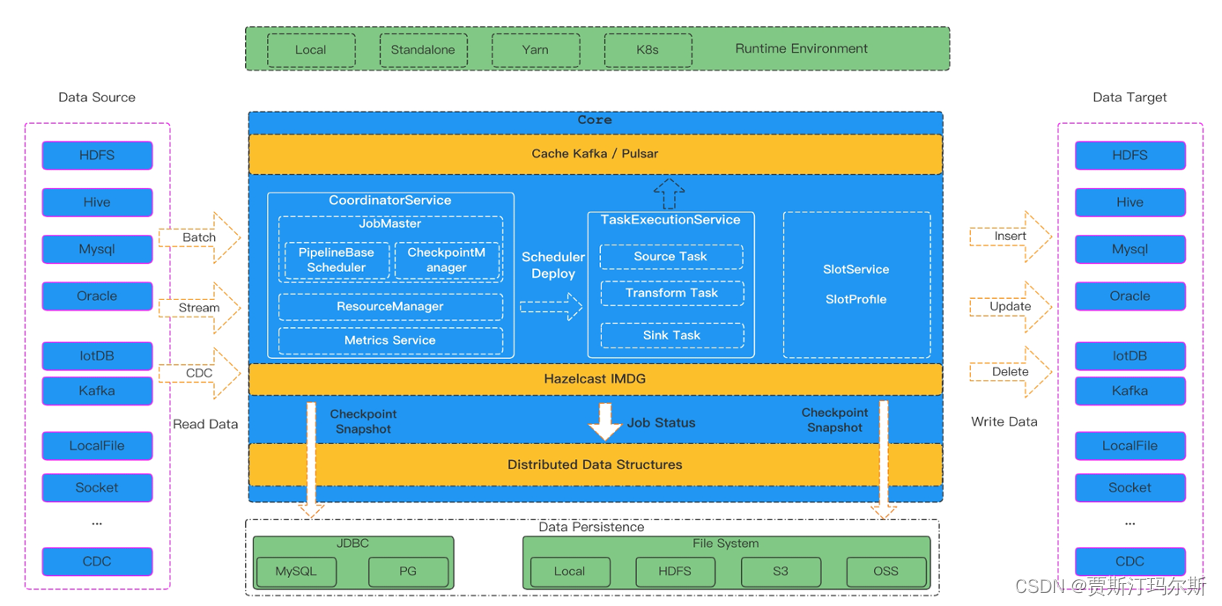
SeaTunnel 与 DataX 、Sqoop、Flume、Flink CDC 对比
产品概述 Apache SeaTunnel 是一个非常易用的超高性能分布式数据集成产品,支持海量数据的离线及实时同步。每天可稳定高效同步万亿级数据,已应用于数百家企业生产,也是首个由国人主导贡献到 Apache 基金会的数据集成顶级项目。 SeaTunnel 主要解决数据集成领域的常见问题:…...

深入理解汇编:平栈、CALL和RET指令详解
视频学习下载地址:https://pan.quark.cn/s/04e6946a803a 汇编语言以其接近硬件的特性和高效的执行速度,在系统编程、性能优化和逆向工程中占有不可或缺的地位。本文将深入探讨汇编语言中的平栈操作以及CALL和RET指令&#…...
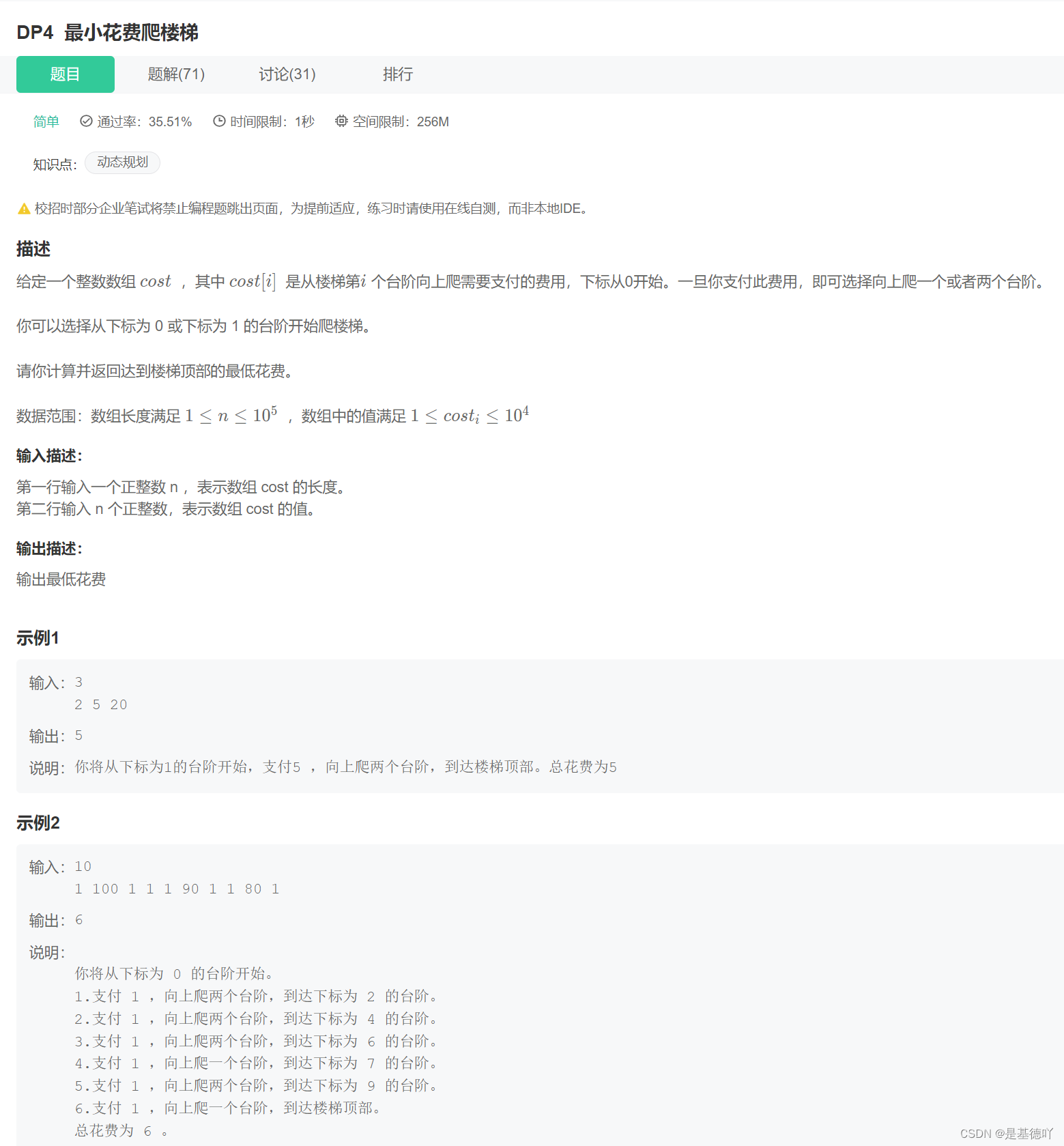
DP4 最小花费爬楼梯
原题链接:最小花费爬楼梯_牛客题霸_牛客网 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 dp。 开一个dp数组和a数组。dp[i]表示在当前这一格所需要的费用,a数组其实就是题目中的cost数组。 因为最后要求到顶楼的最低费用&a…...

OpenXR API概览与核心组件解析
在虚拟现实(VR)和增强现实(AR)领域,OpenXR API提供了一个重要的开放标准,使得开发者能够跨多种硬件和软件平台创建兼容的应用。本文将详细解释OpenXR中的核心组件和数据结构,并探讨它们如何共同…...
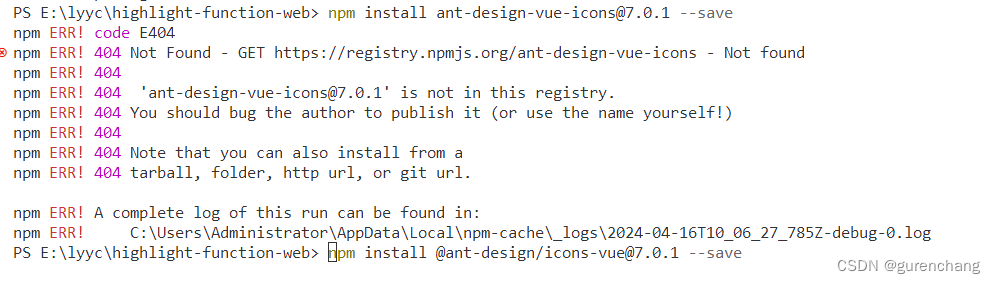
安装指定版本的ant-design-vue和指定版本的@ant-design/icons-vue 图标组件包
前言: 最近在完成公司的项目时,为了兼容其他的版本,需要安装指定版本的ant-design-vue和ant-design/icons-vue 图标组件包,安装成功之后,分享如下: 安装命令: ant-design-vue: 不…...

Zynq7000系列中的休眠模式
休眠模式是在系统层面定义的,它包括将APU置于待机模式,并将多个控制器保持在无时钟的复位状态。 进入休眠模式可以大大降低功耗。在休眠模式下,大多数功能时钟组都会被关闭或断电。唯一需要保持活动的设备是一个CPU、窥探控制单元(…...

在redhat7/8平台上部署ELK7.17.18的技术方案
部署环境说明 为节省资源直接使用1台测试机模拟3节点elasticsearch服务集群做部署,在该主机上同时部署了3个elasticsearch实例、1个logstash实例、1个kibana实例、1个filebeat实例。对于生产环境,以上实例服务应该做分布式部署。 ELK-TEST1 192.168.10…...
分享6个好用的ChatGPT)
(Chat For Al,创新Al,汇语Al助手,AiTab新标签,万能助手,LLaVA)分享6个好用的ChatGPT
目录 1、Chat For AI 2、创想AI 3、汇语AL助手...

MySQL-锁篇
文章目录 表级锁和行级锁了解吗?有什么区别?行级锁使用有什么注意事项?InnoDB有哪几类行锁?共享锁和排他锁是什么?意向锁有什么用? 锁是一种常见的并发事务的控制方式 表级锁和行级锁了解吗?有什…...

滤波器笔记(杂乱)
线性相位是时间平移,相位不失真 零、基础知识 1、用相量表示正弦量 https://zhuanlan.zhihu.com/p/345546880 https://www.zhihu.com/question/347763932/answer/1103938667 A s i n ( ω t θ ) ⇔ A e j θ ⇔ A ∠ θ Asin(\omega t\theta) {\Leftrightarrow…...
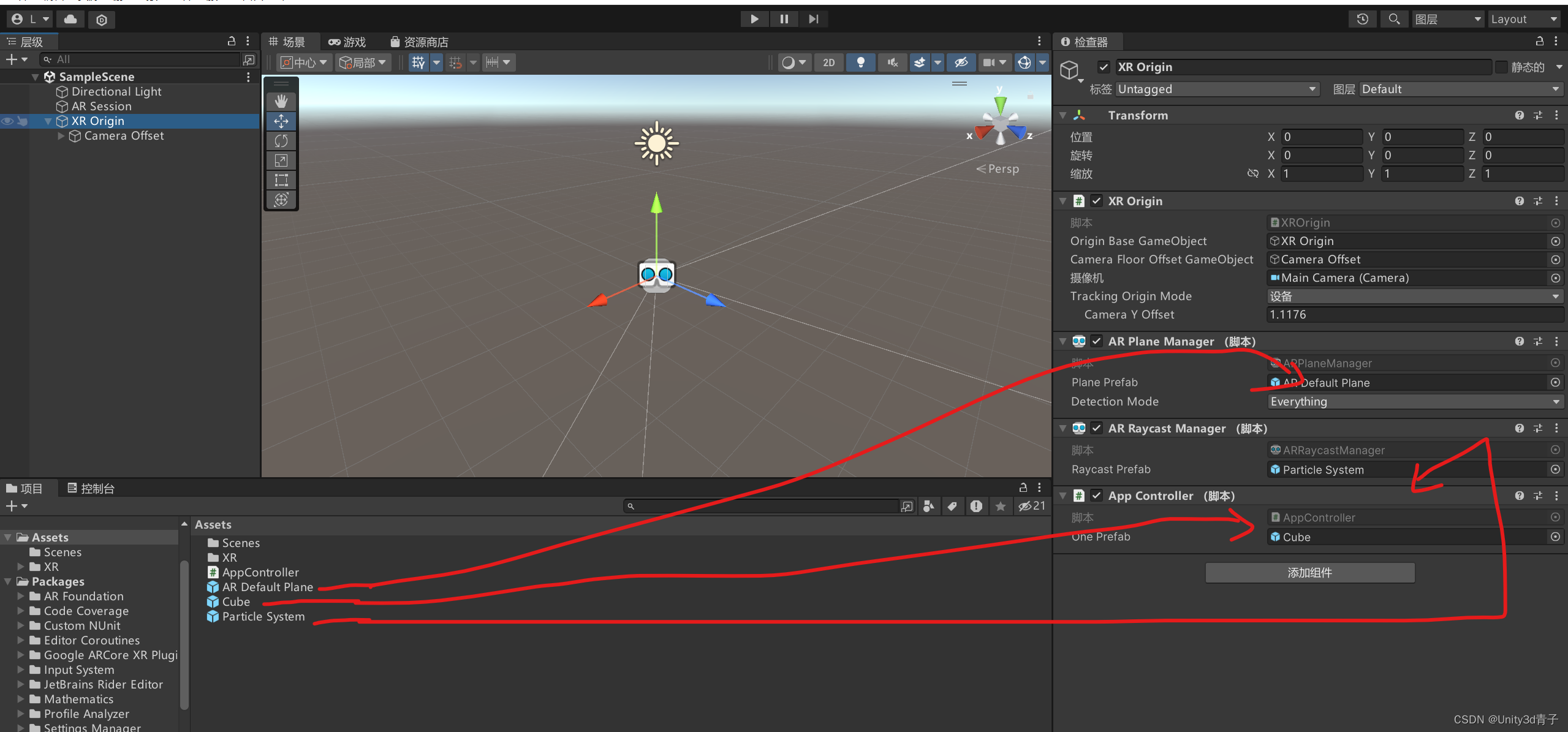
【ARFoundation自学01】搭建AR框架,检测平面点击位置克隆物体
Unity开发ARFoundation相关应用首先安装ARFoundation包 然后设置XR 1.基础AR场景框架搭建 2.一个基本的点击克隆物体到识别的平面脚本 挂在XROrigin上 脚本AppController 脚本说明书 ## 业务逻辑 AppController 脚本旨在实现一个基本的 AR 应用程序功能:用户通过…...

.Net ajax 接收参数
后端部分代码 一般处理程序 public void ProcessRequest(HttpContext context){context.Response.ContentType "text/plain";string str_index context.Request.Form.AllKeys.Contains("index") ? context.Request.Form["index"].ToString(…...

智能零售:引领购物新时代
智能零售通过整合人工智能、物联网、大数据和机器学习等技术,正在彻底改变传统的购物模式,为消费者和零售商提供前所未有的效率和个性化体验。 智能零售利用消费者数据分析来提供个性化的购物推荐。无论是在线平台或是实体店内,智能系统都能…...

【AIGC】AIGC在虚拟数字人中的应用:塑造未来互动体验的革新力量
🚀 🚀 🚀随着科技的快速发展,AIGC已经成为引领未来的重要力量。其中,AIGC在虚拟数字人领域的应用更是引起了广泛关注。虚拟数字人作为一种先进的数字化表达形式,结合了3D建模、动画技术、人工智能等多种先进…...

电机控制器电路板布局布线参考指导(五)
电机控制器电路板布局布线参考指导(五)大容量电容和旁路电容的放置 1.大容量电容的放置2.电荷泵电容器3.旁路电容/去耦电容的放置3.1 靠近电源3.2 靠近功率器件3.3 靠近开关电流源3.4 靠近电流感测放大器3.5 靠近稳压器 tips:资料主要来自网络…...

Python医院挂号脚本
作者介绍:10年大厂数据\经营分析经验,现任大厂数据部门负责人。 会一些的技术:数据分析、算法、SQL、大数据相关、python 欢迎加入社区:码上找工作 作者专栏每日更新: LeetCode解锁1000题: 打怪升级之旅 python数据分析…...
LabVIEW光学探测器板级检测系统
LabVIEW光学探测器板级检测系统 特种车辆乘员舱的灭火抑爆系统广泛采用光学探测技术来探测火情。光学探测器作为系统的关键部件,其探测灵敏度、响应速度和准确性直接关系到整个系统的运行效率和安全性。然而,光学探测器在长期使用过程中可能会因为灰尘污…...
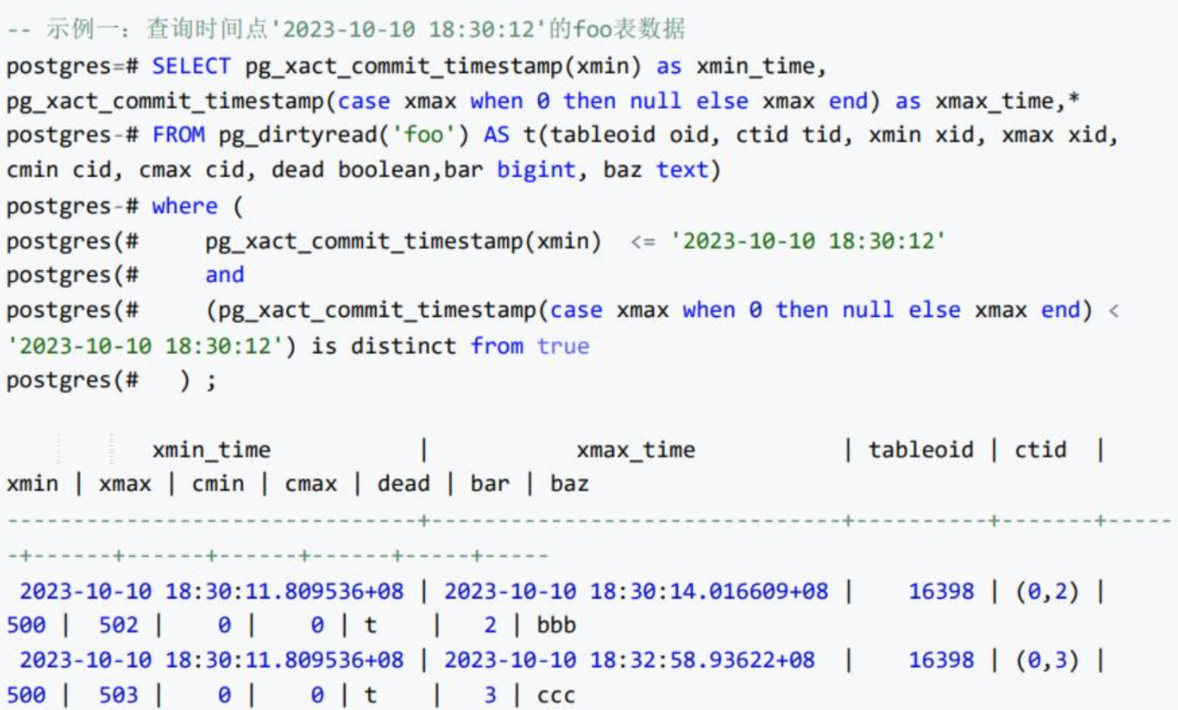
女上司问我:误删除PG百万条数据,可以闪回吗?
作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验 擅长主流数据Oracle、MySQL、PG、openGauss运维 备份恢复,安装迁移,性能优化、故障应急处理等可提供技术业务: 1.DB故障处理/疑难杂症远程支援 2.Mysql/PG/Oracl…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
