2024年MathorCup数学建模A题移动通信网络中PCI规划问题解题文档与程序
2024年第十四届MathorCup高校数学建模挑战赛
A题 移动通信网络中PCI规划问题
原题再现:
物理小区识别码(PCI)规划是移动通信网络中下行链路层上,对各覆盖小区编号进行合理配置,以避免 PCI 冲突、PCI 混淆以及 PCI 模3 千扰等现象。PCI 规划对于减少物理层的小区间互相干扰(ICI),增加物理下行控制信道(PDCCH)的吞吐量有着重要的作用,尤其是对于基站小区覆盖边缘的用户和发生信号切换的用户,能有效地降低信号干扰,提升用户的体验。在一个移动通信系统中,PCI的数量是十分有限的,但实际网络中小区的数量巨大,因此必须对 PCI进行复用,这就带来了PCI 资源的合理复用配置的问题。错误的 PCI配置方式会显著地增加下行网络的ICI,从而会严重影响网络质量。为了降低ICI,在进行 PCI规划时需要综合地考虑同频邻区之间的三种场景:PCI冲突、PCI混淆以及 PCI模3千扰。
在无线通信系统中,如果小区i的主控连接的设备同时可以接收到小区i的信号,则称小区i为小区i的邻区。如果小区j与小区i的频点相同,则小区j是小区i的同频邻区。如果小区i的某主控连接设备接收到小区i的信号强度p,与邻区j的信号强度P,的差小于等于给定门限8,即p-p,≤6:则称小区i为小区i的重叠覆盖邻区。
PCI 冲突发生在主控小区和其同频邻区分配了相同的PCI的情况下,如图1所示,小区1和它的一个同频邻小区2被分配了相同的 PCI值A,此时便会发生 PCI 冲突。应被小区1连接的用户设备可能会错误地连接到小区 2,但小区1才是真正要连接的目标小区。由于对于用户设备来说很难有效地区分场强相差不大的小区1和小区2的信号,错误的连接判断最终会导致无线信号服务的中断,最终导致下行网络资源的错误分配。
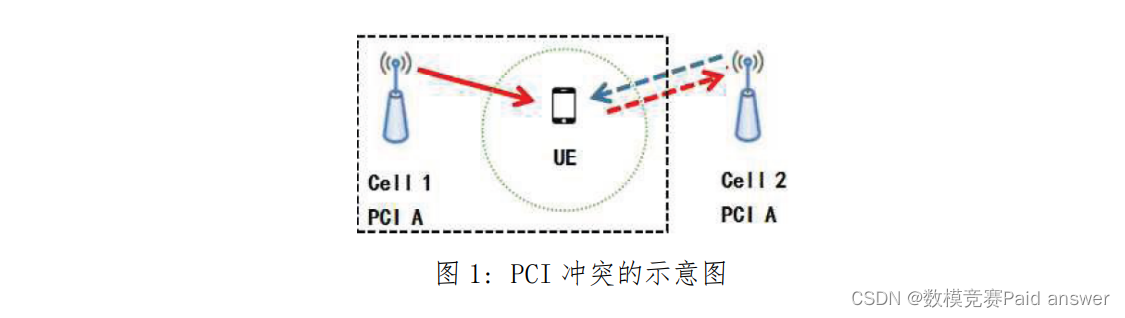
PCI 混淆通常发生在一个主控小区的两个或者多个同频邻区之间,如图2所示。设小区1的两个邻小区2和3被分配了相同的PCI值B,当小区1中的用户由于移动等原因需要切换连接到小区2时,由于小区2和小区3的 PCI相同,用户很可能错误的切换到小区 3。PCI混淆会导致下行网络中的用户在进行服务切换时的信号中断和资源的错误分配。
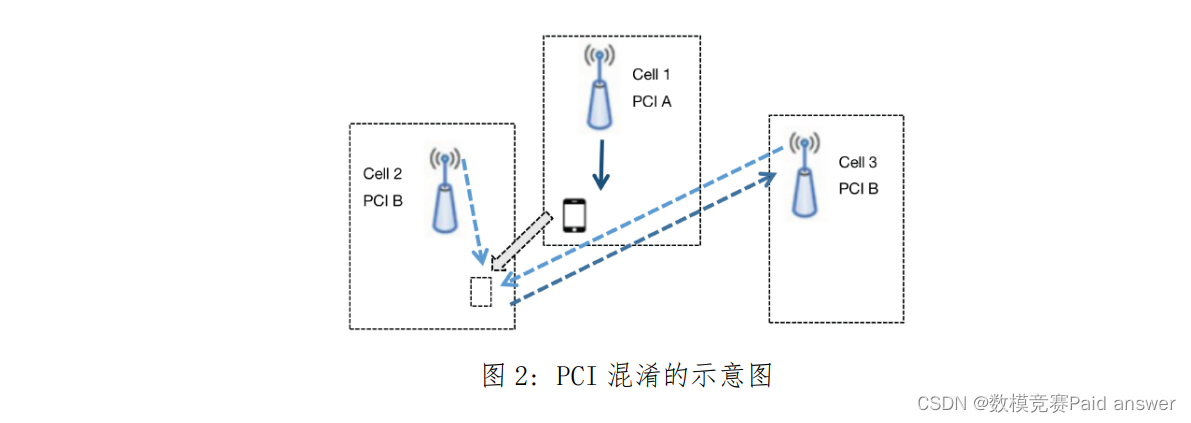
PCI 模3千扰发生在主控小区和其同频重叠覆盖邻区分配的 PCI 模 3相同的情况下,如图3所示,小区1和它的一个同频重叠覆盖邻小区2被分配了模3 相同的 PCI值(例如小区1分配的 PCI是1,小区2分配的 PCI是 7,则小区1和2的 PCI模3的值相同,都是1),此时便会发生PCI模3 千扰。当 PCI 模3 干扰现象发生时,由于小区1和小区2的参考信号的相互叠加,用户设备接收的信号质量会明显的下降,同时这种现象会造成COI的错误评估和下行网络的延迟。

PCI规划问题的目标就是,给每个小区分配PCI,使网络中的PCI冲突、混淆和模3千扰的尽量的少。
实际网络中,表示 PCI 冲突混淆和模3干扰数量的方式有很多,可以用路测数据点的情况,也可以对整个城市进行栅格化用所有栅格的情况,这些方法中,网优部门最常用的就是测量报告(MR)数据。MR数据是UE 设备在通信过程中定时上报的报告,每条 MR 数据中,主要包括 UE 通信时接入的主控小区及接收到的邻区信息以及相应的信号强度值。由于测量报告是定间隔时间上报,因此 MR 数据的分布情况基本可以反映业务量的分布情况。同时,由于 MR 数据在时间和空间上的全面性,因此用 MR数据的冲突、混淆和模3干扰的数量,来反映网络中的 PCI 指标,是比较准确的。
基于 MR 数据的 PCI规划问题具体为:给定N个小区,遍历这些小区的全部 MR数据,生成3个NxN的矩阵,分别为:
冲突矩阵A=[aij]MN,其中若小区i和j同频,则aij的值为小区i为主控,j为邻区的 MR 数量,否则aij的值为 0。
混淆矩阵B=[bij]NN,其中若小区i和j同频,则bij的值为小区i和j同时为另一个小区k的邻区的 MR 数量,否则bij的值为 0。
干扰矩阵C=[cij] ,其中若小区i和j同频,则c的值为小区i为主控,j为i的重叠覆盖邻区的 MR 数量,否则cij的值为 0。
若小区i和j分配相同的PCI值,则冲突数增加aij +aji,混淆数增加bij +bji,如果小区 i和 j分配的 PCI 模3 的值相同,则模3 干扰数增加cij +cji。
实际网络中,总共可分配的PCI是0到1007 共1008个。根据附件提供的数据,对某区域中 2067 个小区进行 PCI规划。
问题 1:给这 2067 个小区重新分配 PCI, 使得这 2067 个小区之间的冲突 MR 数、混淆 MR 数和模 3 干扰 MR 数的总和最少。
问题 2:考虑冲突、混淆和干扰的不同优先级,给这 2067 个小区重新分配 PCI,也是考虑这 2067 个小区之间的冲突、混淆和模3 干扰。首先保证冲突的 MR 数降到最低,在此基础上保证混淆的 MR 数降到最低,最后尽量降低模3 干扰的 MR 数。实际网络中,给这 2067 个小区重新分配PCI,会对这些小区以外的一些距离较近的小区产生影响,也就是这些小区和外围小区之间会产生冲突混淆和模 3 干扰的 MR 数的变化。
问题 3:给这 2067 个小区重新分配 PCI,使得所有可能被影响到的小区间的冲突 MR 数、混淆 MR 数和模3 干扰 MR 数的总和最少。
问题 4:考虑冲突、混淆和干扰的不同优先级,给这2067 个小区重新分配 PCI, 也是考虑所有可能被影响到的小区间的冲突、混淆和模3 千扰。首先保证冲突的MR数降到最低,在此基础上保证混淆的MR数降到最低,最后尽量降低模3 干扰的 MR 数。
注:上面四个问题中,除了正常完成论文外,每个问题对 2067 个小区分配的 PCI 都填入“问题结果表.xlsx”文件对应的四个表单中,并单独上传至竞赛平台。
程序代码:
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
#你不仅长得帅,想的还挺美#你不仅长得帅,想的还挺美
相关文章:

2024年MathorCup数学建模A题移动通信网络中PCI规划问题解题文档与程序
2024年第十四届MathorCup高校数学建模挑战赛 A题 移动通信网络中PCI规划问题 原题再现: 物理小区识别码(PCI)规划是移动通信网络中下行链路层上,对各覆盖小区编号进行合理配置,以避免 PCI 冲突、PCI 混淆以及 PCI 模3 千扰等现象。PCI 规划…...

Learn something about front end——颜色
好装的标题啊哈哈哈哈哈哈 最近get了一个学习前端的网站叫FreeCodeCamp 原色:rgb三个值的其中一个值拉满,比如说rgb(255,0,0)是红色这样,三个主色: 红色 rgb(255, 0, 0) #FF0000绿色 rgb(0, 255, 0) #00FF00蓝色 rgb(0, 0, …...

各大厂都推出鸿蒙APP了,你就一定要学习一下鸿蒙APP测试了!
2023年8月,华为推出鸿蒙4.0,由于其广泛的用户基础和品牌传播力,在短短几个月的时间,使用鸿蒙4.0系统的设备就达到千万级别,并且在9月份发售Mate 6之后,还在装机量的增长更加迅猛。 基于此,11月…...
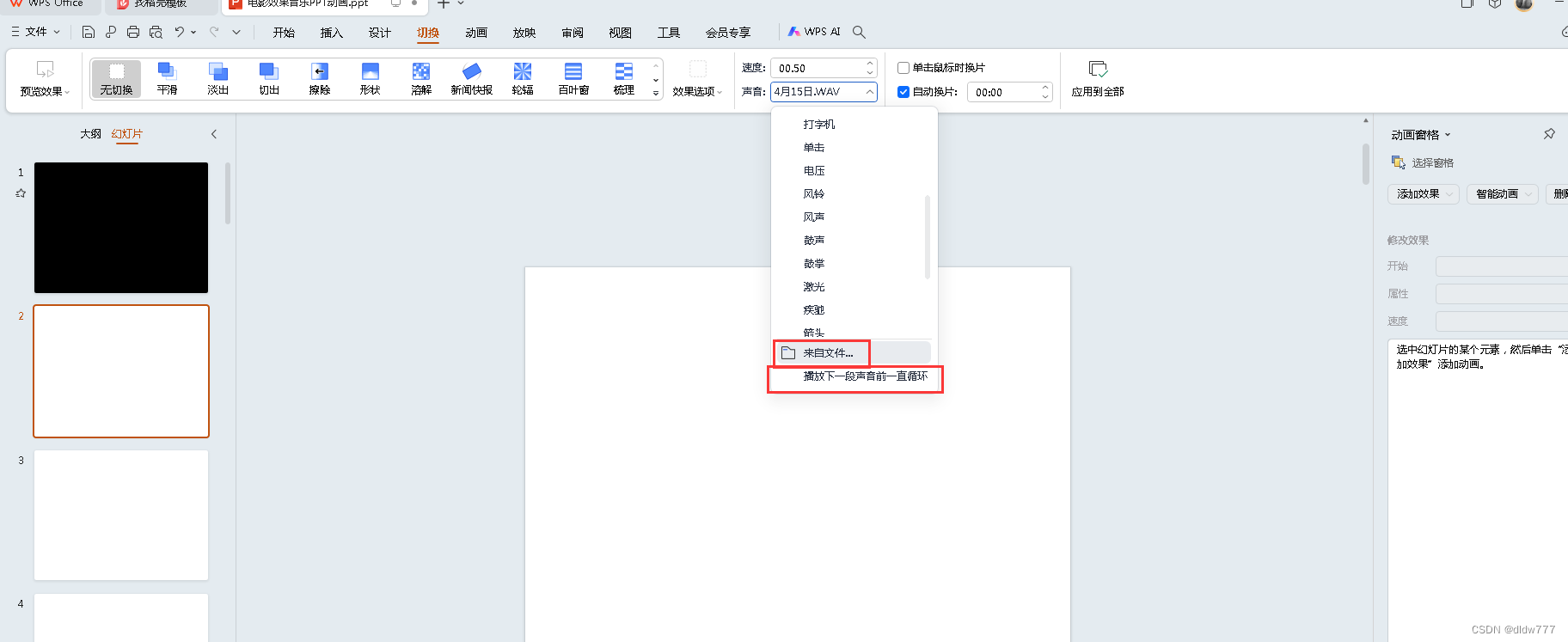
ppt里的音乐哪里来的?
心血来潮,想照着大神的模板套一个类似于快闪的ppt。 ppt里是有一段音乐的,那段音乐就是从幻灯片第二页开始响起的。 但是我就找不到音乐在哪。 甚至我把ppt里的所有素材都删除了,再看动画窗格,仍然是空无一物,显然&…...

【算法】标签算法及其运作流程
标签算法 1. 标签算法及其运作流程2. 标签算法主要有哪些?3.用python语言举例实现聚类 1. 标签算法及其运作流程 标签算法是一种用于自动为数据或文本内容添加标签或分类的算法。这些标签可以帮助组织、检索和理解数据,是信息管理和数据挖掘中的重要工具…...
【数据结构】习题之链表的回文结构和相交链表
👑个人主页:啊Q闻 🎇收录专栏:《数据结构》 🎉前路漫漫亦灿灿 前言 今日的习题是关于链表的,分别是链表的回文结构和相交链表的判断。 链表的回文结构 题目为:链表的回文结…...
5个常见的前端手写功能:New、call apply bind、防抖和节流、instanceof、ajax
实现New 首先创建一个新的空对象设置原型,将对象的原型设置为函数的prototype对象让函数的this指向这个对象,执行构造函数的代码判断函数的返回值类型,如果是值类型,返回创建的对象。如果是引用类型,就返回这个引用类…...

WPF 跨线程-Dispatcher:详解与示例
在 WPF 应用程序中,UI 线程负责处理用户界面元素的所有操作,例如绘制、布局和事件处理。由于 WPF 控件是线程敏感的,只能在 UI 线程上访问它们。如果我们想在后台线程中执行 UI 操作,我们就需要使用 Dispatcher 来确保这些操作在正…...

[c++][netcdf]通过c\c++读取字段的scale_factor与add_offset
函数:c void readScaleAndOffset(const char* FileName,const char* VarName) {NcFile dataFile(FileName, NcFile::read);NcVar Varf dataFile.getVar(VarName);//查看维度cout << "XSizef" << Varf.getDim(0).getSize() << endl;co…...

技术速递|.NET 智能组件简介 – AI 驱动的 UI 控件
作者:Daniel Roth 排版:Alan Wang AI 的最新进展有望彻底改变我们与软件交互和使用软件的方式。然而,将 AI 功能集成到现有软件中可能面临一些挑战。因此,我们开发了新的 .NET 智能组件,这是一组真正有用的 AI 支持的 …...
保护C#代码的艺术:深入浅出代码混淆技术
摘要 在C#开发中,代码的保护是一个不可忽视的问题。本文深入探讨了几种常用的C#代码混淆工具,帮助开发者理解如何有效地保护代码不被反编译。同时,本文也对混淆技术的优缺点进行了分析,并提供了一些实际使用的建议。 引言 C#是…...

多线程CountDownLatch使用
1、简介 CountDownLatch是一个同步工具类,用来携调多个线程之间的同步,它是是使用一个计数器进行实现的,计数器初始值为线程数量。当每一个线程完成自己任务后,计数器的值就会减1。当计数器的值为0时,表示所有的线程都…...

高校心理教育辅导系统|基于Springboot的高校心理教育辅导系统设计与实现(源码+数据库+文档)
高校心理教育辅导系统目录 目录 基于Springboot的高校心理教育辅导系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、学生功能模块的实现 (1)学生登录界面 (2)留言反馈界面 (3)试卷列表界…...
:App层)
Rockchip Android13 Vold(三):App层
目录 前言 一:处理Volumes 1、接收StorageVolume 2、创建MediaVolume 3、附加MediaVolume...
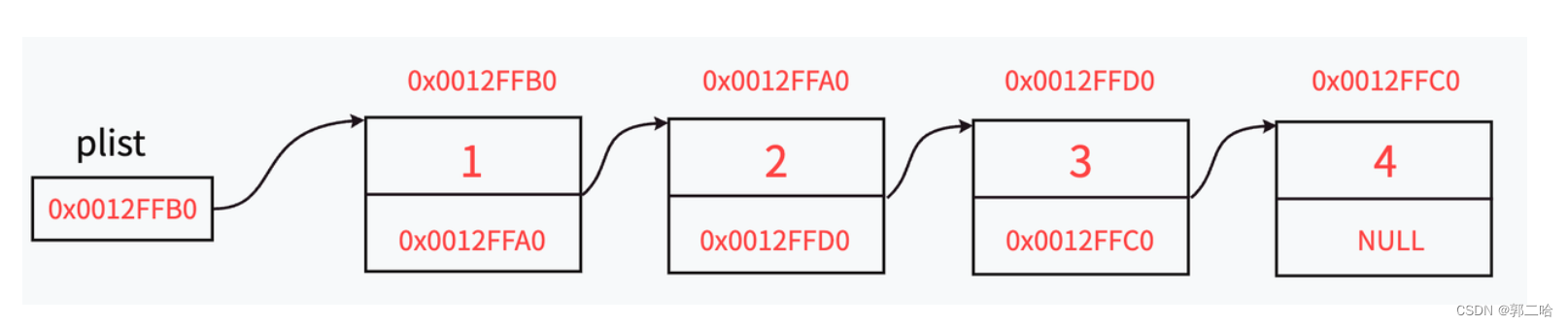
数据结构——单链表(C语言版)
文章目录 一、链表的概念及结构二、单链表的实现SList.h链表的打印申请新的结点链表的尾插链表的头插链表的尾删链表的头删链表的查找在指定位置之前插入数据在指定位置之后插入数据删除pos结点删除pos之后的结点销毁链表 三、完整源代码SList.hSList.ctest.c 一、链表的概念及…...
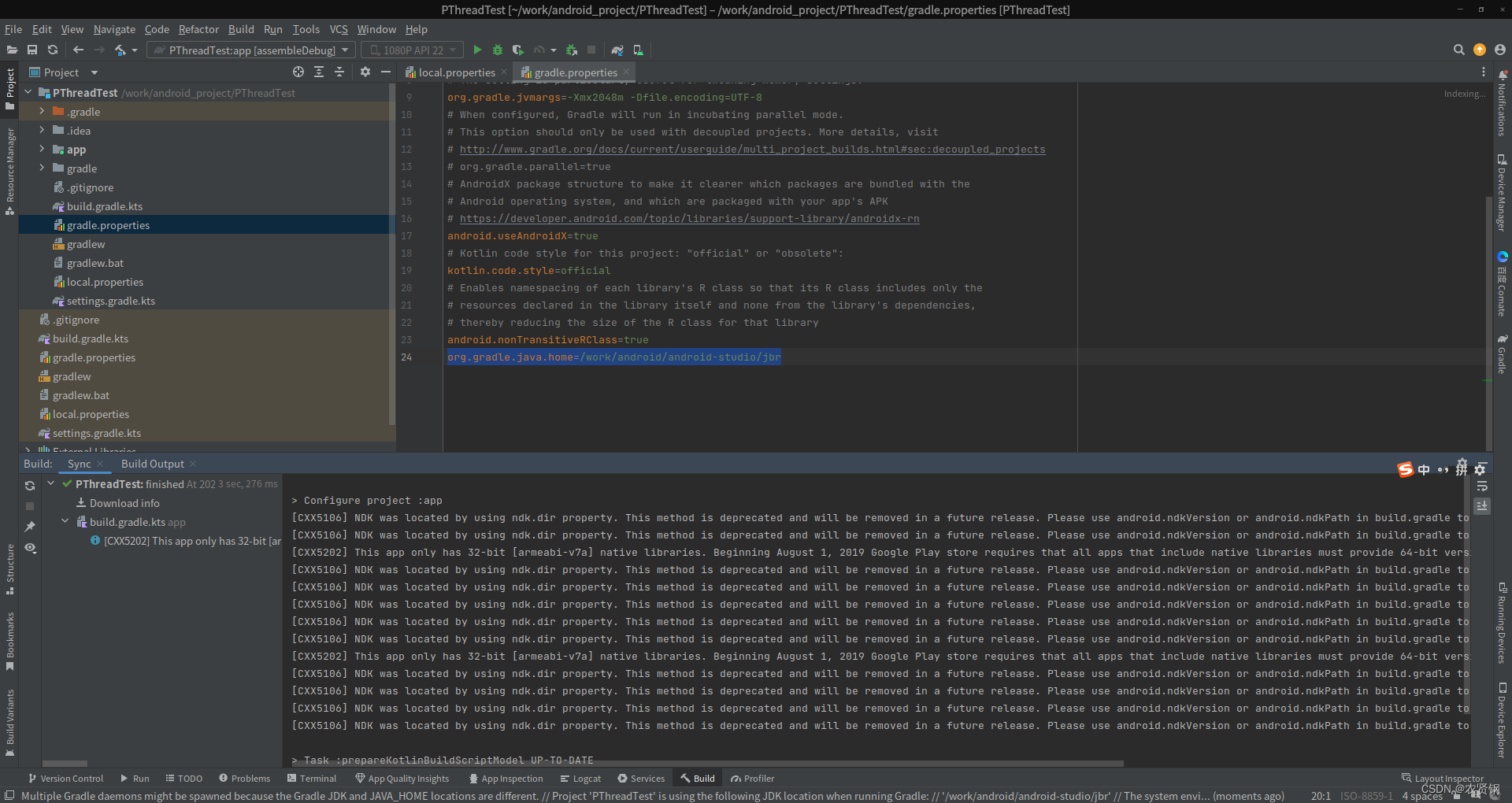
:app debug:armeabi-v7a failed to configure C/C++
报错信息 由于刚换电脑不久,新建native c工程时,出现报错如下: :app debug:armeabi-v7a failed to configure C/C null java.lang.NullPointerExceptionat com.android.build.gradle.tasks.CmakeQueryMetadataGenerator.getProcessBuilder(…...
DHCP和套接字编程)
计算机网络——应用层(4)DHCP和套接字编程
一、动态主机配置协议DHCP 1、关于协议配置: 在协议软件中,给协议参数赋值的动作就叫协议配置一个协议软件在使用前必须已被正确配置,具体的配置信息取决于协议栈连接到互联网的计算机的协议软件需要正确配置的参数包括①IP地址;…...
TF-IDF演算法(Term Frequency - Inverse Document Frequency)最好懂筆記
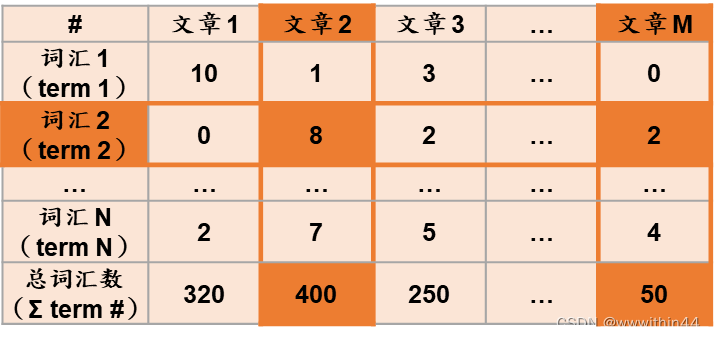
前情提要 BoW (Bag of Words) 演算法 假设现在有M篇文章,一共使用了N个词汇(term),我们就可以将文章转换成以下类型的矩阵,其中column1和row1的“10”表示“文章1”中出现了10次“词汇1”,“文章1”也可以…...
2024年4月最新版GPT
2024年4月最新版ChatGPT/GPT4, 附上最新的使用教程。 随着人工智能技术的不断发展,ChatGPT和GPT4已经成为了人们日常生活中不可或缺的助手。2024年4月,OpenAI公司推出了最新版本的GPT4,带来了更加强大的功能和更加友好的用户体验。本文将为大家带来最新版GPT4的实用…...
机器学习——模型评价
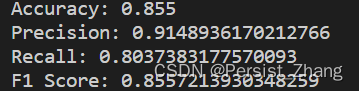
概述 在机器学习中,模型评价是评估和比较不同模型性能的关键步骤之一。它是通过对模型的预测结果与真实标签进行比较,从而量化模型的预测能力、泛化能力和稳定性。模型评价旨在选择最佳的模型,理解模型的行为,并为模型的改进提供…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...
