人工智能揭示矩阵乘法的新可能性
人工智能揭示矩阵乘法的新可能性
数学家酷爱漂亮的谜题。当你尝试找到最有效的方法时,即使像乘法矩阵(二维数字表)这样抽象的东西也会感觉像玩一场游戏。这有点像尝试用尽可能少的步骤解开魔方——具有挑战性,但也很诱人。除了魔方,每一步可能的步数为 18;对于矩阵乘法,即使在相对简单的情况下,每一步都可以呈现超过 10^12 个选项。
在过去的 50 年里,研究人员以多种方式解决了这个问题,所有这些都是基于人类直觉辅助的计算机搜索。2022 年 10 月,人工智能公司 DeepMind 的一个团队展示了如何从一个新的方向解决这个问题,在《Nature》杂志的一篇论文中报告说,他们已经成功地训练了一个神经网络来发现新的快速矩阵乘法算法。就仿佛 AI 找到了解决极其复杂的魔方的未知策略。

论文链接:https://www.nature.com/articles/s41586-022-05172-4
「这是一个非常巧妙的结果。」哥伦比亚大学计算机科学家 Josh Alman 说,但他和其他矩阵乘法专家也强调,这种人工智能辅助将补充而不是取代现有方法——至少在短期内是这样。「这就像对可能成为突破的事物的概念验证。」Alman 说。结果只会帮助研究人员完成他们的任务。
仿佛是为了证明这一点,《自然》杂志的论文发表三天后,两位奥地利研究人员展示了新旧方法如何相互补充。他们使用传统的计算机辅助搜索来进一步改进神经网络发现的一种算法。

论文链接:https://arxiv.org/pdf/2210.04045.pdf
结果表明,就像解决魔方的过程一样,通往更好算法的道路将充满曲折。
乘法矩阵
矩阵乘法是所有数学中最基本和最普遍的运算之一。要将一对 n×n 矩阵相乘,每个矩阵都有 n^2 个元素,你可以将这些元素以特定组合相乘并相加以生成乘积,即第三个 n×n 矩阵。将两个 n×n 矩阵相乘的标准方法需要 n^3 次乘法运算,因此,例如,一个 2×2 矩阵需要八次乘法。

对于具有数千行和列的较大矩阵,此过程很快就会变得麻烦。但在 1969 年,数学家 Volker Strassen 发现了一种使用七个而不是八个乘法步骤将一对 2×2 矩阵相乘的过程,代价是引入了更多的加法步骤。

如果你只想乘以一对 2×2 矩阵,则 Strassen 算法不必要地复杂化。但他意识到它也适用于更大的矩阵。那是因为矩阵的元素本身可以是矩阵。例如,可以将具有 20,000 行和 20,000 列的矩阵重新设想为一个 2×2 矩阵,其四个元素各为 10,000×10,000 矩阵。然后可以将这些矩阵中的每一个细分为四个 5,000×5,000 块,依此类推。Strassen 可以应用他的方法在此嵌套层次结构的每一层上乘以 2×2 矩阵。随着矩阵大小的增加,减少乘法所节省的成本也会增加。
Strassen 的发现促使人们开始寻找高效的矩阵乘法算法,此后启发了两个不同的子领域。一个侧重于一个原则问题:如果你想象将两个 n×n 矩阵相乘并让 n 趋于无穷大,那么最快的算法中的乘法步骤数如何与 n 成比例?
最佳缩放比例的当前记录 n^2.3728596 属于麻省理工学院计算机科学家 Alman 和 Virginia Vassilevska Williams。(最近发布的预印本报告了使用新技术的微小改进。)但这些算法纯粹是理论上的兴趣,仅在荒谬的大矩阵上胜过 Strassen 等方法。

论文链接:https://arxiv.org/abs/2210.10173
第二个子领域的思考规模较小。在 Strassen 的工作之后不久,以色列裔美国计算机科学家 Shmuel Winograd 表明 Strassen 已经达到了理论极限:不可能用少于七个乘法步骤来乘以 2×2 矩阵。但对于所有其他矩阵大小,所需乘法的最小数量仍然是一个悬而未决的问题。小矩阵的快速算法可能会产生巨大的影响,因为当乘以合理大小的矩阵时,这种算法的重复迭代可能会击败 Strassen 的算法。

论文链接:https://www.sciencedirect.com/science/article/pii/0024379571900097
不幸的是,可能性的数量是巨大的。即使对于 3×3 矩阵,「可能的算法数量也超过了宇宙中的原子数量,」DeepMind 研究员兼新工作的负责人之一 Alhussein Fawzi 说。
面对这些令人眼花缭乱的选项,研究人员通过将矩阵乘法转化为一个看起来完全不同的数学问题——一个计算机更容易处理的问题——取得了进展。可以将两个矩阵相乘的抽象任务表示为一种特定类型的数学对象:称为张量的三维数字数组。然后,研究人员可以将这个张量分解为基本分量的总和,称为「rank-1」张量;这些中的每一个都代表相应矩阵乘法算法中的不同步骤。这意味着找到一个有效的乘法算法相当于最小化张量分解中的项数——项越少,涉及的步骤就越少。
通过这种方式,研究人员发现了新的算法,可以使用比标准 n^3 更少的乘法步骤来乘以许多小矩阵大小的 n×n 矩阵。但是,不仅优于标准而且优于 Strassen 小矩阵算法的算法仍然遥不可及——直到现在。
Game On
DeepMind 团队通过将张量分解变成单人游戏来解决这个问题。他们从 AlphaGo 的深度学习算法入手——AlphaGo 是另一个 DeepMind AI,它在 2016 年学会了玩棋盘游戏 Go,足以击败顶尖的人类棋手。
所有的深度学习算法都是围绕神经网络构建的:人工神经元网络被分类成层,连接强度可以变化,代表每个神经元对下一层神经元的影响程度。这些连接的强度在训练过程的多次迭代中得到调整,在此期间神经网络学习将它接收到的每个输入转换为有助于算法实现其总体目标的输出。
在 DeepMind 的新算法(称为 AlphaTensor)中,输入代表通往有效矩阵乘法方案的步骤。神经网络的第一个输入是原始矩阵乘法张量,其输出是 AlphaTensor 为其第一步选择的 rank-1 张量。该算法从初始输入中减去这个 rank-1 张量,产生一个更新的张量,该张量作为新输入反馈到网络中。重复该过程,直到最终起始张量中的每个元素都减少为零,这意味着没有更多的 rank-1 张量可以取出。
在这一点上,神经网络发现了一个有效的张量分解,因为它在数学上保证了所有 rank-1 张量的总和恰好等于起始张量。到达那里所采取的步骤可以转换回相应的矩阵乘法算法的步骤。
游戏是这样的:AlphaTensor 反复将张量分解为一组 rank-1 分量。每次,如果 AlphaTensor 找到减少步数的方法,它就会获得奖励。但胜利的捷径一点也不直观,就像你有时必须在魔方上拼凑出一张完美有序的脸,然后才能解决整个问题。
该团队现在有了一种算法,理论上可以解决他们的问题。他们只需要先训练它。
新路径
与所有神经网络一样,AlphaTensor 需要大量数据进行训练,但张量分解是一个众所周知的难题。研究人员可以为网络提供有效分解的例子很少。相反,他们通过在更简单的逆问题上进行训练来帮助算法开始:将一堆随机生成的 rank-1 张量相加。
布朗大学计算机科学家 Michael Littman 说:「他们正在使用简单的问题为困难的问题生成更多数据。」将这种向后训练过程与强化学习相结合,其中 AlphaTensor 在寻找有效分解时会产生自己的训练数据,其效果比单独使用任何一种训练方法都要好得多。
DeepMind 团队训练 AlphaTensor 来分解代表矩阵乘法的张量,最高可达 12×12。它寻求用于将普通实数矩阵相乘的快速算法,以及特定于更受约束的设置(称为模 2 运算)的算法。(这是仅基于两个数字的数学,因此矩阵元素只能是 0 或 1,并且 1 + 1 = 0。)研究人员通常从这个更受限制但仍然广阔的空间开始,希望这里发现的算法可以适用于实数矩阵。
训练后,AlphaTensor 在几分钟内重新发现了 Strassen 的算法。然后,它针对每种矩阵大小发现了多达数千种新的快速算法。这些与最著名的算法不同,但乘法步骤数相同。
在少数情况下,AlphaTensor 甚至打破了现有记录。它最令人惊讶的发现发生在模 2 运算中,它发现了一种新算法,可以在 47 个乘法步骤中将 4×4 矩阵相乘,比 Strassen 算法两次迭代所需的 49 个步骤有所改进。它还打破了最著名的 5×5 模 2 矩阵算法,将所需的乘法次数从之前的 98 次记录减少到 96 次。(但这个新记录仍然落后于使用 5×5 矩阵击败 Strassen 算法所需的 91 步。)
这一引人注目的新结果引起了很多兴奋,一些研究人员对基于 AI 的现状改进大加赞赏。但并非矩阵乘法领域中的每个人都对此印象深刻。「我觉得它有点被夸大了,」Vassilevska Williams 说。「这是另一种工具。这不像是,[哦,计算机打败了人类,] 你知道吗?」
研究人员还强调,破纪录的 4×4 算法的直接应用将受到限制:它不仅只在模 2 算法中有效,而且在现实生活中,除了速度之外还有其他重要的考虑因素。
Fawzi 也认为,这仅仅是个开始。「有很大的改进和研究空间,这是一件好事,」他说。
最后的转折
相对于成熟的计算机搜索方法,AlphaTensor 的最大优势也是它最大的弱点:它不受人类直觉的约束,无法判断好的算法是什么样子的,因此它无法解释自己的选择。这使得研究人员很难从其成就中学习。
但这可能并没有看上去那么大的缺点。在 AlphaTensor 结果公布几天后,奥地利林茨大学(JKU)的数学家 Manuel Kauers 和他的研究生 Jakob Moosbauer 报告说又向前迈进了一步。

Manuel Kauers 调整了 DeepMind 的方法以产生进一步的改进。——Jakob Moosbauer
当 DeepMind 论文发表时,Kauers 和 Moosbauer 正在使用传统的计算机辅助搜索来寻找新的乘法算法。但与大多数以新的指导原则重新开始的此类搜索不同,他们的方法通过反复调整现有算法来工作,希望从中节省更多的乘法。以 AlphaTensor 的 5×5 模 2 矩阵算法为起点,他们惊奇地发现,他们的方法在短短几秒钟的计算之后,就将乘法步骤从 96 步减少到了 95 步。
AlphaTensor 还间接帮助他们进行了另一项改进。此前,Kauers 和 Moosbauer 并没有费心去探索 4×4 矩阵的空间,他们认为不可能击败 Strassen 算法的两次迭代。AlphaTensor 的结果促使他们重新考虑,在从头开始计算一周后,他们的方法出现了另一种 47 步算法,与 AlphaTensor 发现的算法无关。「如果有人告诉我们 4×4 有什么值得发现的东西,我们本可以早点做到这一点,」Kauers 说。「但是,好吧,这就是它的工作原理。」
Littman 预计会有更多这样的惊喜,他将这种情况比作跑步者第一次在四分钟内跑完一英里,这一壮举曾被广泛认为是不可能的。「人们就像,[哦,等等,我们可以做到这一点,] 现在很多人都可以做到,」他说。
展望未来,Fawzi 希望推广 AlphaTensor 以解决更广泛的数学和计算任务,就像它的祖先 AlphaGo 最终扩展到其他游戏一样。
Kauers 认为这是将机器学习应用于发现新算法的真正试金石。他指出,寻求快速矩阵乘法算法是一个组合问题,无论有无人工协助,计算机搜索都非常适合。但并不是所有的数学问题都那么容易确定。他说,如果机器学习能够发现一种全新的算法理念,「这将改变游戏规则。」
相关文章:

人工智能揭示矩阵乘法的新可能性
人工智能揭示矩阵乘法的新可能性 数学家酷爱漂亮的谜题。当你尝试找到最有效的方法时,即使像乘法矩阵(二维数字表)这样抽象的东西也会感觉像玩一场游戏。这有点像尝试用尽可能少的步骤解开魔方——具有挑战性,但也很诱人。除了魔方…...

实在智能携手长江新零售俱乐部:探秘实在Agent数字员工,开启零售品牌增长新篇章
近日,实在智能携手长江新零售俱乐部成功举办了“AIGC:数字员工助力零售品牌新增长”主题活动,成功吸引了二十余家企业中高层管理精英的踊跃参与。在此次活动中,与会者围绕零售业数字化转型的当前态势、面临的挑战及其重要性进行了…...

计算机科学与导论 第十七 十八章 计算理论,人工智能
文章预览: 计算理论17.1 引言17.2 简单语言17.3 图灵机邱奇 -图灵 论题 人工智能引言18.1.1 什么是人工智能18.1.2 智能体18.1.3 编程语言 18.2 知识的表示18.2.1 语义网18.2.2 框架18.2.3 谓词逻辑18.2.4 基于规则的系统 18.2 专家系统18.3 语言理解18.4 搜索18.5 …...
linux 设置定时任务---学习
1、设置定时任务 crontab -e 设置格式参考:【Linux】Linux crontab 命令定时任务设置_crontab 设置每天10:30执行-CSDN博客 测试过程: */1 * * * * /root/cronjob.sh 脚本内容: echo "hell0 cronjob" >> /root/test/hello.txt 实现…...

钡铼IOy系列模块深挖工业场景需求提供丰富多样的I/O解决方案
钡铼IOy系列模块以其灵活性和多样性,在工业场景中提供了丰富多样的I/O解决方案,满足了不同行业、不同应用场景的需求。以下是一些常见的工业场景需求及钡铼IOy系列模块提供的解决方案: 1. 工厂自动化 需求:工厂自动化需要对生产线…...

【刷题笔记】第三天
两道简单题 文章目录 [2923. 找到冠军 I](https://leetcode.cn/problems/find-champion-i/description/)[3095. 或值至少 K 的最短子数组 I](https://leetcode.cn/problems/shortest-subarray-with-or-at-least-k-i/description/) 2923. 找到冠军 I 方法1: 如果 i …...
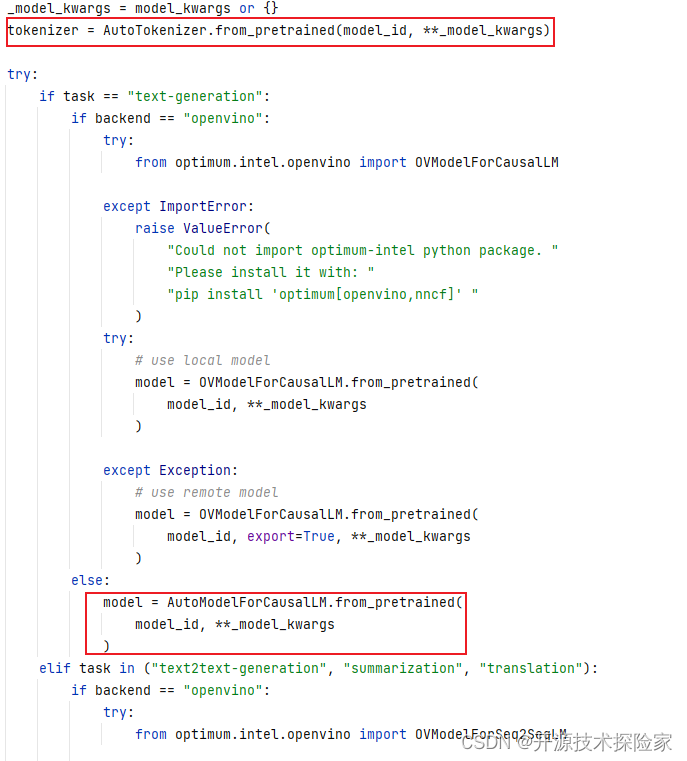
开源模型应用落地-LangChain试炼-CPU调用QWen1.5(一)
一、前言 尽管现在的大语言模型已经非常强大,可以解决许多问题,但在处理复杂情况时,仍然需要进行多个步骤或整合不同的流程才能达到最终的目标。然而,现在可以利用langchain来使得模型的应用变得更加直接和简单。 通过langchain框…...
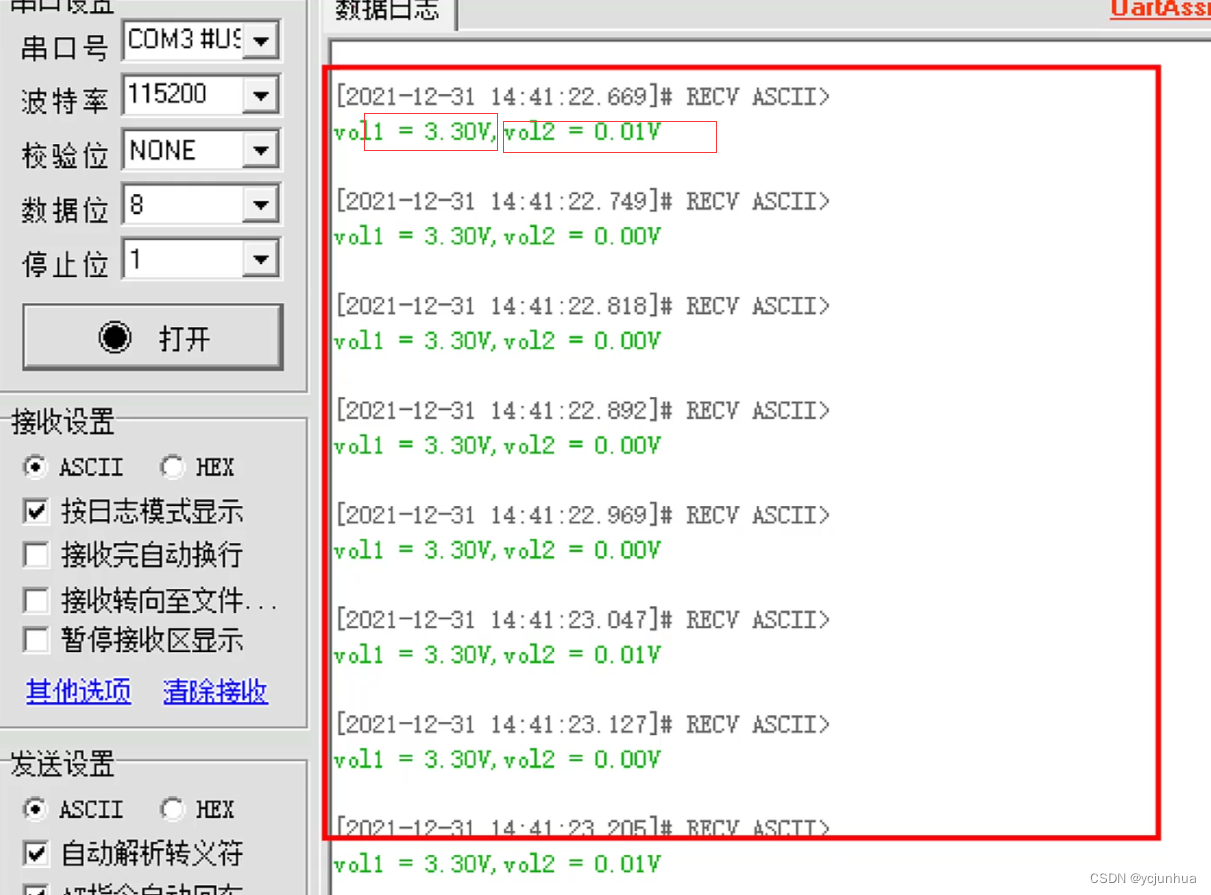
STM32-模数转化器
ADC(Analog-to-Digital Converter) 指模数转换器。是指将连续变化的模拟信号转换 为离散的数字信号的器件。 ADC相关参数说明: 分辨率: 分辨率以二进制(或十进制)数的位数来表示,一般有 8 位、10 位、12 位、16 位…...

算法刷题记录2
4.图 4.1.被围绕的区域 思路:图中只有与边界上联通的O才不算是被X包围。因此本题就是从边界上的O开始递归,找与边界O联通的O,并标记为#(代表已遍历),最后图中剩下的O就是:被X包围的O。图中所有…...

中国代工巨头旗下芯片公司遭网络攻击,千兆字节数据被泄露
近日,中国智能手机代工巨头闻泰科技旗下荷兰芯片制造商Nexperia发布声明,称其遭遇网络攻击,有未经授权的第三方访问了公司的 IT 服务器,目前已向相关部门报告了此次事件,并与网络安全专家合作开启调查。而据相关消息&a…...
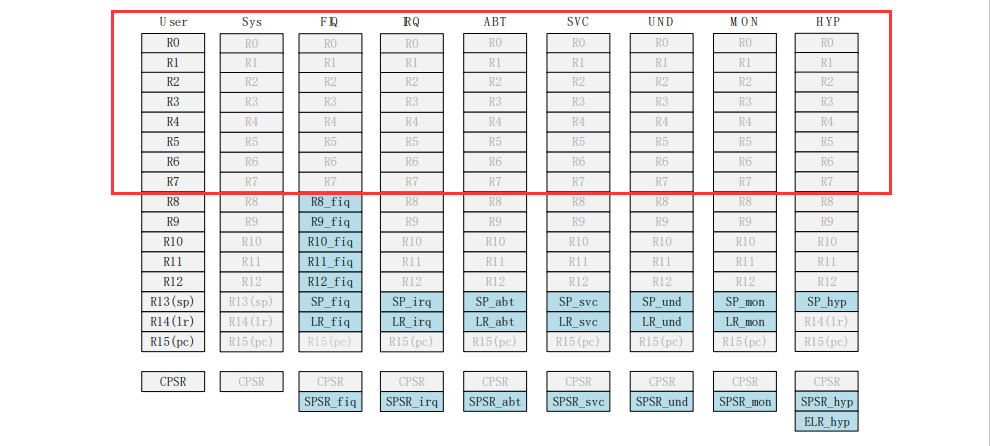
【ARM 裸机】汇编 led 驱动之基本语法
我们要编写的是 ARM 汇编,编译使用的是 gcc 交叉编译器,所以要符合 GNU 语法。 1、汇编指令 汇编由一条条指令构成,ARM 不能直接访问存储器,比如 RAM 中的数据,I.MX6UL 中的寄存器就是 RAM 类型的,我们用…...
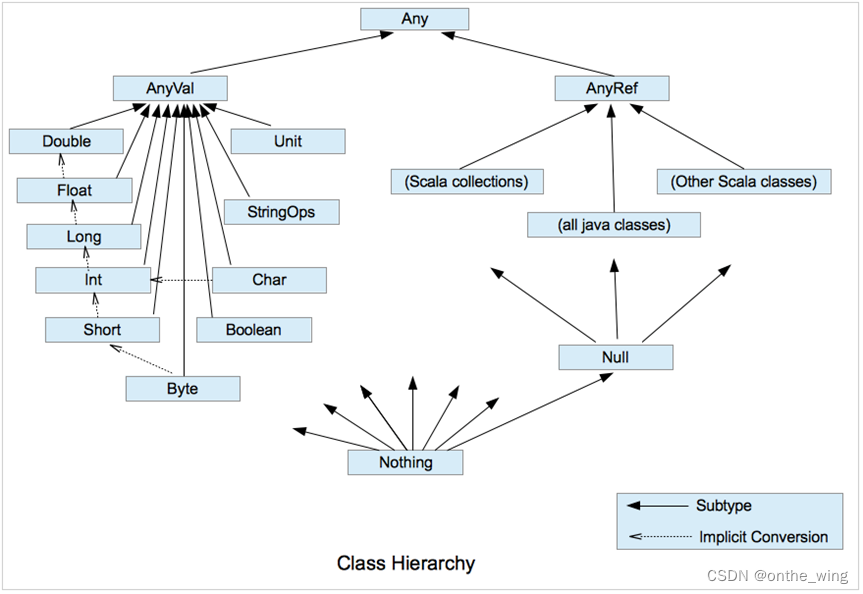
scala---基础核心知识(变量定义,数据类型,流程控制,方法定义,函数定义)
一、什么是scala Scala 是一种多范式的编程语言,其设计初衷是要集成面向对象编程和函数式编程的各种特性。Scala运行于Java平台(Java虚拟机),并兼容现有的Java程序。 二、为什么要学习scala 1、优雅 2、速度快 3、能融合到hado…...
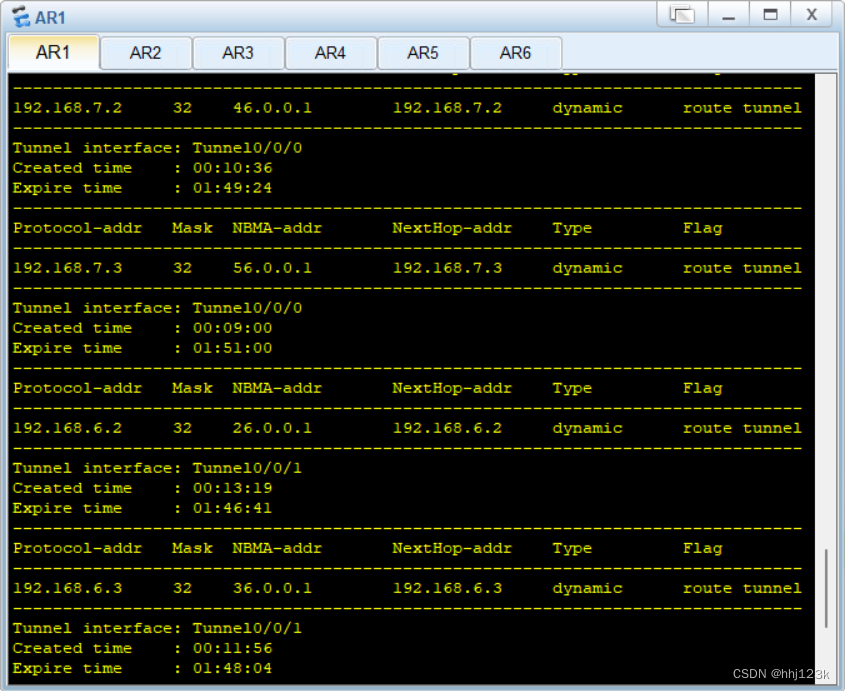
OSPF星型拓扑和MGRE全连
一,拓扑 二,要求 1,R6为ISP只能配置IP地址,R1-R5的环回为私有网段 2,R1/4/5为全连的MGRE结构,R1/2/3为星型的拓扑结构, 3,R1为中心站点所有私有网段可以互相通讯,私有网段…...
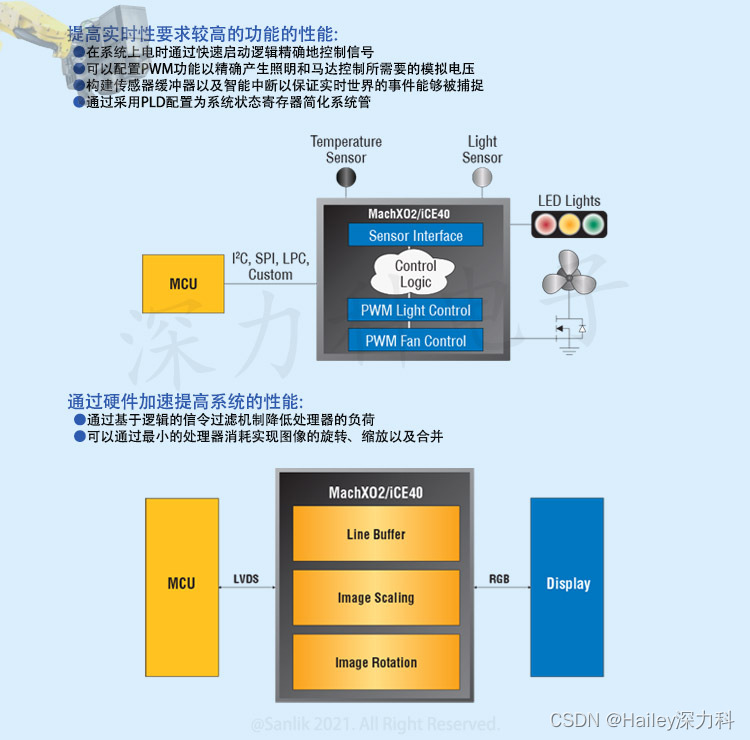
智能时代中的工业应用中前所未有的灵活桥接和I/O扩展功能解决方案MachXO2系列LCMXO2-1200HC-4TG100I FPGA可编程逻辑IC
lattice莱迪斯 MachXO2系列LCMXO2-1200HC-4TG100I超低密度FPGA现场可编程门阵列,适用于低成本的复杂系统控制和视频接口设计开发,满足了通信、计算、工业、消费电子和医疗市场所需的系统控制和接口应用。 瞬时启动,迅速实现控制——启动时间…...
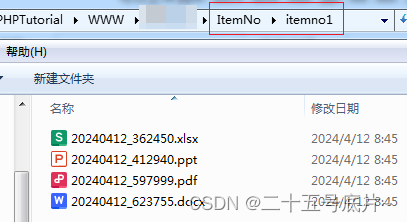
php:实现压缩文件上传、解压、文件更名、压缩包删除功能
效果图 1.上传文件 2.压缩包文件 3.itemno1文件 或 4.上传到系统路径\ItemNo 5.更名后的itemno1文件(命名:当天日期六位随机数) 代码 <form action"<?php echo htmlspecialchars($_SERVER[PHP_SELF], ENT_QUOTES, UTF-8); ?>" methodpost en…...
【机器学习】科学库使用第5篇:Matplotlib,学习目标【附代码文档】
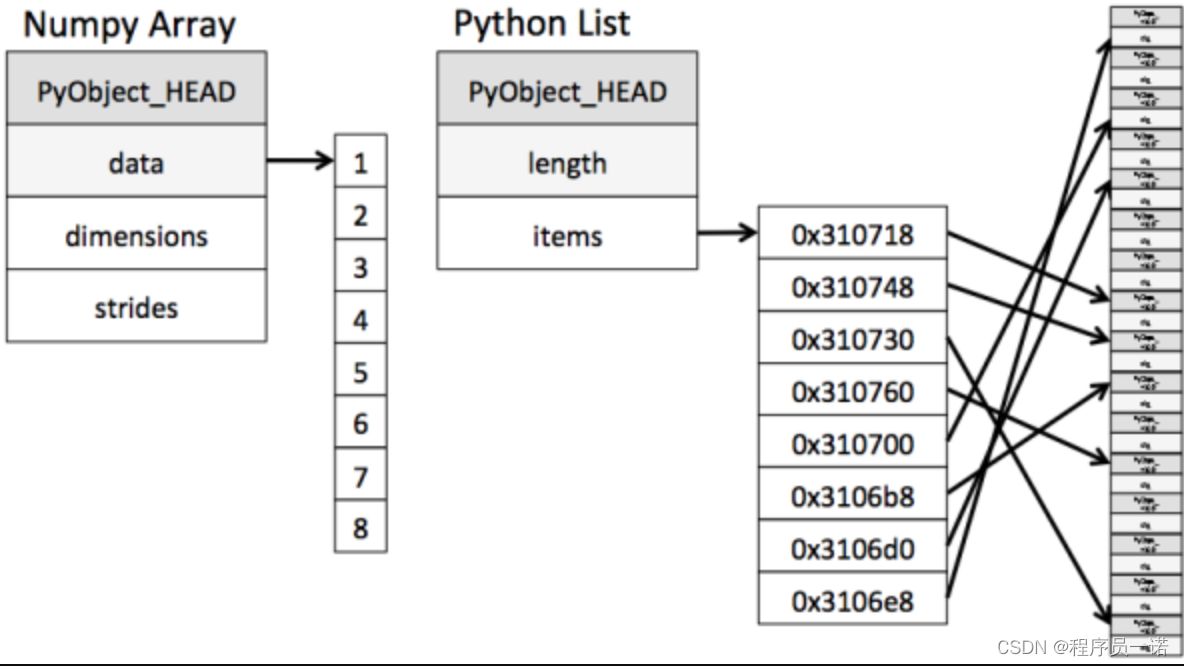
机器学习(科学计算库)完整教程(附代码资料)主要内容讲述:机器学习(常用科学计算库的使用)基础定位、目标,机器学习概述定位,目标,学习目标,学习目标,1 人工智能应用场景,2 人工智能小…...
Java面试八股文(JVM篇)(❤❤)
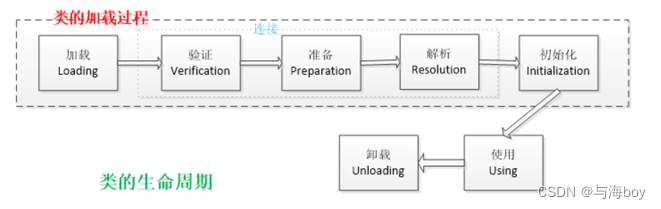
Java面试八股文_JVM篇 1、知识点汇总2、知识点详解:3、说说类加载与卸载11、说说Java对象创建过程12、知道类的生命周期吗?14、如何判断对象可以被回收?17、调优命令有哪些?18、常见调优工具有哪些20、你知道哪些JVM性能调优参数&…...

「51媒体」如何有效进行媒体邀约,提升宣传传播效果?
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 进行有效的媒体邀约,提升宣传传播效果的关键在于策略性和专业性。以下是具体的做法: 明确目标:要确立清晰的品牌推广目标和策略,包括确定目…...

docker初始化进程
docker run --init 是一个 Docker 命令的选项,用于在容器中运行一个初始化进程(通常是 tini)。这个初始化进程负责处理一些 Unix 信号(如 SIGTERM 和 SIGCHLD),并确保容器中的进程能够正确地被管理和清理。…...

基于快照行情的股票/基金 1分钟 K 线合成指南
1. 概述 由于不同交易所不同资产的交易规则是有差异的,导致不同交易所基于快照行情或逐笔成交合成不同资产1分钟 K 线的计算方法是不同的。 本教程旨在提高 DolphinDB 在具体业务场景下的落地效率,降低 DolphinDB 在实际业务使用中的开发难度。 本教程…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...
