python实现k_means聚类
K-Means算法是将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的数据,在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。
簇中所有数据的均值通常被称为这个簇的“质心”(Centroids)。在一个二维平面中,一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值,质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。
算法实现:
一、随机取n个点,即想要分类数目
二、将当前数据每个点都与取到的n个点进行作差,将差值最小的分为一类
三、将分好类的结果取出计算均值,取出每个类中和均值距离最小的值,将其做为新的中心点
四、重复上述步骤,直到最终分成的簇内结果不再发生变化(在当前的算法里,我们连续验证三次,即在三次内,结果不再发生变化,迭代就会停止)
#k均值计算
import numpy as np
import pandas as pd
import random
import math
def data():
rand_value = [random.randint(1,10000) for i in range(10000)]
# print(rand_value)
# rand_value = [63, 23, 93, 52, 33, 84, 34, 91, 52, 68, 64, 4, 3, 58, 37, 76, 75, 52, 49, 34, 91, 29, 67, 42, 97, 69, 99, 9, 15,
# 44, 12, 46, 86, 92, 10, 67, 46, 93, 49, 29, 93, 95, 60, 33, 30, 63, 24, 45, 26, 47, 12, 62, 50, 54, 13, 62, 40, 39,
# 32, 2, 92, 34, 20, 72, 68, 37, 88, 32, 84, 28, 88, 85, 5, 88, 56, 30, 5, 3, 43, 9, 13, 62, 44, 11, 90, 97, 80, 34,
# 12, 90, 56, 54, 87, 59, 20, 51, 58, 54, 29, 32]
return rand_value
#进行计算,并返回质心及详细信息
def k_mean(data_list,k,rand_choice):
# rand_choice = [random.choice(data_list) for i in range(k)]
temp_dict = {}
for i in range(len(data_list)):
temp_list = []
for j in range(len(rand_choice)):
#解决符号差异带来的影响
temp_list.append(abs(abs(data_list[i]) - abs(rand_choice[j])))
insert_index = temp_list.index(min(temp_list))
if temp_dict.get(rand_choice[insert_index]):
temp_dict[rand_choice[insert_index]].append(data_list[i])
else:
temp_dict[rand_choice[insert_index]] = [data_list[i]]
return temp_dict
#输出距离均值最近的点,返回新的质心及中心点
def min_distince(data_dict):
k_list = []
k_keys = list(data_dict.keys())
for j in range(len(k_keys)):
data_list = data_dict[k_keys[j]]
mean_value = sum(data_list)/len(data_list)
for i in range(len(data_list)):
if i == 0:
distance_value = abs(data_list[i] - mean_value)
s = 0
# distance_list.append(distance_value)
else:
if distance_value > abs(data_list[i] - mean_value):
s = i
distance_value = min(distance_value,abs(data_list[i] - mean_value))
k_list.append(data_list[s])
# distance_list.append(distance_value)
return k_list
def iteration(source_data,k):
iter_num = 0
end_list = []
if len(source_data) < k:
print('需要计算的数据量少于要分类的数据量,请检查数据源\n')
else:
while True:
iter_num += 1
print('迭代次数%d'%iter_num)
if iter_num == 1:
data_dict = k_mean(source_data,k,[random.choice(source_data) for i in range(k)])
end_list.append(data_dict)
# print(data_dict)
result = min_distince(data_dict)
# result = min_distince(k_mean(source_data,k,[random.choice(source_data) for i in range(k)]))
else:
data_dict = k_mean(source_data,k,result)
end_list.append(data_dict)
# print(data_dict)
result = min_distince(data_dict)
if len(end_list) == 4:
del end_list[0]
if end_list[0] == end_list[1] and end_list[1] == end_list[2]:
print(data_dict)
break
if __name__ == '__main__':
source_data = data()
iteration(source_data,5)
相关文章:

python实现k_means聚类
K-Means算法是将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的数据,在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。簇中所有数据的均值通常被称为这个簇的“质心”(Centroids)。在一个二维平面中ÿ…...

【批处理脚本】-3.3-exit命令详解
"><--点击返回「批处理BAT从入门到精通」总目录--> 共3页精讲(列举了所有exit的用法,图文并茂,通俗易懂) 在从事“嵌入式软件开发”和“Autosar工具开发软件”过程中,经常会在其集成开发环境IDE(CodeWarrior,S32K DS,Davinci,EB Tresos,ETAS…)中,…...

如果读了我2011年求职前端开发的酸爽经历,希望你可以鼓起勇气继续向前
今年是2023年,如果你觉得今年找工作很难,狗哥回忆了一下2011年求职前端开发工作的酸爽经历,希望你读了以后可以鼓起勇气,不要迷茫,简历投出去石沉大海的,需要改简历的就赶紧改,刷题不到位的就赶…...
)
PTA:L1-016 查验身份证、L1-017 到底有多二、L1-018 大笨钟(C++)
目录 PTA:L1-016 查验身份证 问题描述: 实现代码: L1-017 到底有多二 问题描述: 实现代码: L1-018 大笨钟 问题描述: 实现代码: 都是简单模拟题,不再写题解。 PTA…...

springboot工厂模式解决if_else流程和问题点解决
一、主要问题点 spring中的Bean由IOC容器进行管理,和普通工厂的区别就是springboot中的类不能通过自己New出来使用,如果通过new写入到工厂,涉及到相关实现类调用其他Service(该service在正确情况下正常注入)ÿ…...

如何避免缓存击穿?使用GO语言实现sliglefight
前言 在缓存系统中,如果发生了缓存未命中,通常会向数据库或者其他的缓存系统来请求数据。 想象这样一种情况,缓存系统中某个热点值被删除了,随后一大批请求到来,造成大量的cache miss,如果这些请求全部都…...
【浅学Java】MySQL索引七连炮
MySQL索引面试七连炮0. 谈一下你对索引的理解1. MySQL索引原理和数据结构能介绍一下吗2. B树和B树的区别3. MySQL聚簇索引和非聚簇索引的区别4. 使用MySQL索引都有什么原则4.1 回表4.2 索引覆盖4.3 最左匹配4.4 索引下推5. 不同的存储引擎是如何进行数据的存储的6. MySQL组合索…...

扬帆优配|昔日白马股濒临退市,却6天5涨停!ST股突然集体爆发
尽管再度重申“公司股票将被停止上市”,但3月8日早间,*ST辅仁股价仍是在开盘后快速封住涨停板。这已是该公司近6个买卖日来,第5次呈现涨停。 无独有偶,8日早间ST东瀛也在此前多次涨停后,再度呈现近4%的涨幅。而就在7日…...

Git 基础(一)—— Git 的安装及其配置
目录 一、Git 的下载与安装 1、Linux 环境 2、Windows 环境 (1) 下载 Git 安装包 (2) 安装 Git 二、Git 配置 1、配置用户信息 2、查看配置信息 3、Windows 环境下配置文件的位置 一、Git 的下载与安装 1、Linux 环境 在保证网络环境畅通的情况下,直接输…...

什么是信息安全风险评估?企业如何做?
什么是信息安全风险评估? 信息安全风险评估是参照风险评估标准和管理规范,对信息系统的资产价值、潜在威胁、薄弱环节、已采取的防护措施等进行分析,判断安全事件发生的概率以及可能造成的损失,提出风险管理措施的过程。当风险评…...
HBase---idea操作Hbase数据库并且映射到Hive
idea操作Hbase数据库并且映射到Hive 文章目录idea操作Hbase数据库并且映射到Hiveidea操作Hbase数据库环境准备启动服务创建Maven工程在测试类中编写初始化方法在测试类中编写关闭方法在测试类中编写创建命名空间方法在测试类中编写创建表方法在测试类中编写查看表结构方法在测试…...
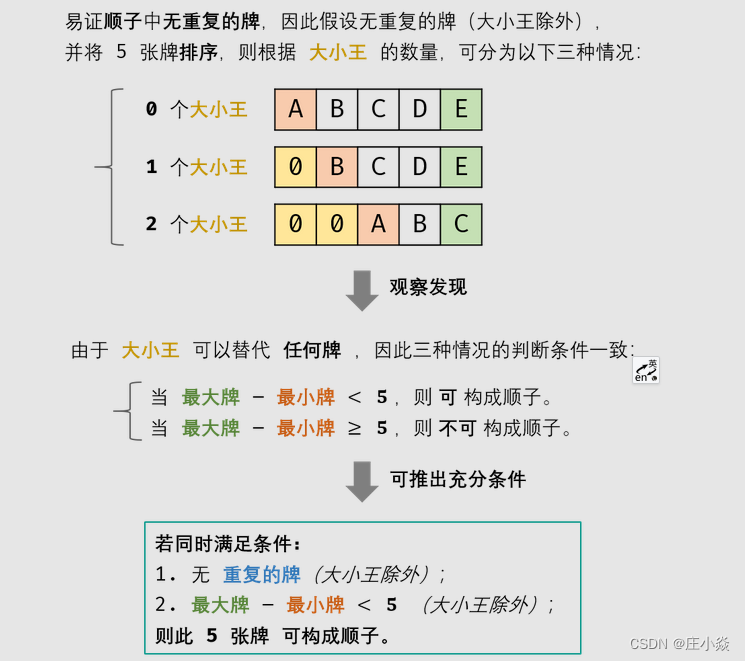
剑指 Offer 61 扑克牌中的顺子
摘要 扑克牌中的顺子 一、集合 Set 遍历 根据题意,此5张牌是顺子的 充分条件 如下: 除大小王外,所有牌 无重复 ;设此5张牌中最大的牌为max,最小的牌为min(大小王除外),则需满足…...
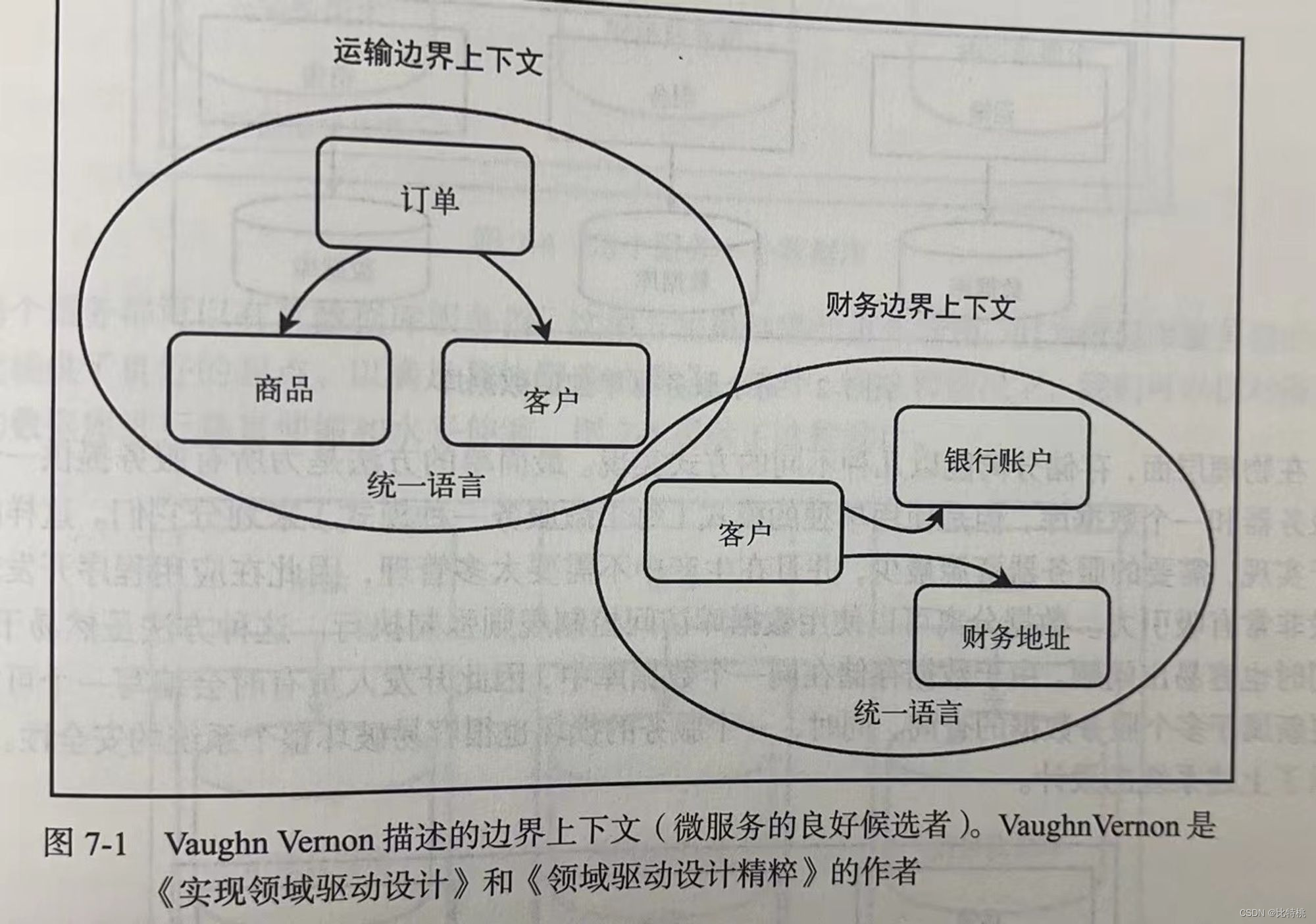
Spring 响应式编程-读书笔记
序言 大家好,我是比特桃。本文为《Spring 响应式编程》的读书笔记,响应式技术栈可以创建极其高效、易于获取且具有回弹性的端点,同时响应式可以容忍网络延迟,并以影响较小的方式处理故障。响应式微服务还可以隔离慢速事务并加速速…...
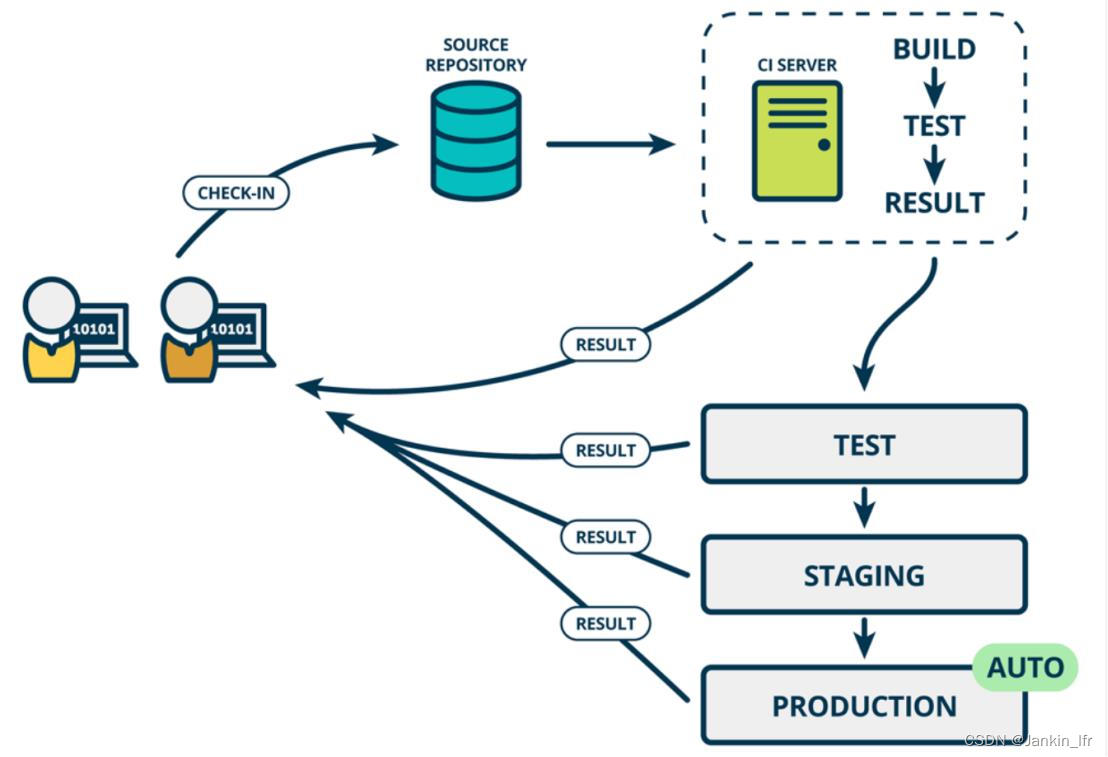
CI流水线的理解
一、概念 单元测试:针对软件的基本单元(如:类、函数)所做的测试。 集成测试:将软件代码单元集成起来后,以组件、模块和子系统为单位进行的测试,主要测试接口间的交互关系。也称组件测试…...
OpenStack手动分布式部署Nova【Queens版】
目录 Nove简介: 1、登录数据库配置(在controller执行) 1.1登录数据库 1.2数据库里创建nova-api 1.3数据库登录授权 1.4创建nova用户 1.5添加admin用户为nova用户 1.6创建nova服务端点 1.7创建compute API 服务端点 1.8创建一个placement服务…...

centos7 oracle19c安装 ORA-01012: not logged on
总共分三步 1.下载安装包:里面有一份详细的安装教程 链接:https://pan.baidu.com/s/1Of2a72pNLZ-DDIWKrTQfLw?pwd8NAx 提取码:8NAx 2.安装后,执行初始化:时间较长 /etc/init.d/oracledb_ORCLCDB-19c configure 3.配置环境变量,不配置环境变量,sq…...

山东小巨人申报条件
国家专精特新小巨人特点1、经济效益:上年度企业营业收入在1亿元至4亿元之间,近2年主营业务收入或净利润的平均增长率达到10%以上,企业资产负债率不高于70%。2、专业化程度:(1)企业从事特定细分市场时间达到…...

手写中实现并学习ahooks——useRequest
前言 最近业务没有之前紧张了,也是消失了一段时间,也总结了一些之前业务上的问题。 和同事沟通也是发现普通的async await 封装api在复杂业务场景下针对于请求的业务逻辑比较多,也是推荐我去学习一波ahooks,由于问题起源于请求…...

[手写OS]动手实现一个OS 之 准备工作以及引导扇区
[手写OS]动手实现一个OS之第一步-环境以及引导扇区 环境准备 一台可用计算机(linux我不知道,我用的Windows)汇编编译器NASM一个方便的软盘读写工具VirtualBox 汇编编译器NASM 官网地址:https://www.nasm.us/pub/nasm/snapshot…...

JVM实战OutOfMemoryError异常
目录 Java堆溢出 常见原因: 虚拟机栈和本地方法栈溢出 实验1:虚拟机栈和本地方法栈测试(作为第1点测试程序) 实验2:(作为第1点测试程序) 运行时常量池和方法区溢出 运行时常量池内存溢出 …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...
