31. 下一个排列
题目描述
整数数组的一个排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的下一个排列是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。 类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须原地修改,只允许使用额外常数空间。
示例1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例3:
输入:nums = [1,1,5]
输出:[1,5,1]
解题思路
根据题目描述,这里得到两个限制条件:1,在原来的基础上增加 2,增加的要是最少
- 第一个条件:将后面的大数和前面的小数进行交换,即可增大数值。如13456,将6和3交换就可以得到一个更大的数16453
- 第二个条件:交换的数尽可能的靠后,如将5和6交换得到的数13465会比16453小。此外,对第一个交换位置后的数字进行升序排列,将大数往后移,即可以得到更小的数值,如将6和3进行交换后得到16453,再将第一个交换位置6后面的数字进行升序排列,得到16345,会比原来大,但是数值更小了。
故可以总结出算法(这里就使用题解给出的算法):
- 首先从后向前查找第一个顺序对 (i,i+1),满足 a[i]<a[i+1]。这样「较小数」即为 a[i]。此时 [i+1,n)必然是下降序列。
- 如果找到了顺序对,那么在区间 [i+1,n)中从后向前查找第一个元素 j 满足a[i]<a[j]。这样「较大数」即为 a[j]。
- 交换 a[i]与 a[j],此时可以证明区间 [i+1,n)必为降序。我们可以直接使用双指针反转区间 [i+1,n)使其变为升序,而无需对该区间进行排序。
拿一个序列举例:
输入:[5, 4, 7, 5, 3, 2]
输出:[5, 5, 2, 3, 4, 7]
首先从后往前找到第一个元素,使a[i]<a[i+1],即为4,定位较小数
然后从后往前找到第一个元素,使a[j]>a[i],即为5,定位较大数
将较小数和较大数进行交换,得到5,5,7,4,3,2
对较小数位置后面的数进行升序排列,得到5,5,2,3,4,7,即为最终答案
代码
class Solution {public void nextPermutation(int[] nums) {// 判断是否使降序数组,降序数组直接返回升序结果int flag = 0;for(int i = 0;i < nums.length-1; i++){if(nums[i] < nums[i+1]){flag = 1;break;}}if(flag == 0){// 若数组是完全降序排列,则变为升序即可Arrays.sort(nums);}else{int p = 0, q = 0;// 找到较小数for(q = nums.length-2; q >= 0; q --)if(nums[q] < nums[q+1])break;// 找到较大数for(p = nums.length-1; p > q; p --)if(nums[q] < nums[p])break;// 交换两个数swap(nums, p, q);// 将较小数索引后面的数按升序排列,因为是降序排列,所以只需要逆置即可reverse(nums, q+1);}}public void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}public void reverse(int[] nums, int start) {int left = start, right = nums.length - 1;while (left < right) {swap(nums, left, right);left++;right--;}}
}
相关文章:

31. 下一个排列
题目描述 整数数组的一个排列 就是将其所有成员以序列或线性顺序排列。 例如,arr [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。 整数数组的下一个排列是指其整数的下一个字典序更大的排列。更正式地&…...

Android笔记: mkdirs不生效失败
Manifest已经配置权限,代码中也动态获取权限,mkdirs一直返回false File.mkdirs()方法创建文件夹失败 1、动态申请读写权限 <!--SDCard写权限--> <uses-permission android:name="android.permission.WRITE_EXTERNAL_STORAGE" /> <!--SDCard读权…...
——贪心+构造)
需要添加的硬币的最小数量(Lc2952)——贪心+构造
给你一个下标从 0 开始的整数数组 coins,表示可用的硬币的面值,以及一个整数 target 。 如果存在某个 coins 的子序列总和为 x,那么整数 x 就是一个 可取得的金额 。 返回需要添加到数组中的 任意面值 硬币的 最小数量 ,使范围 …...

军工保密资质介绍及申请要求
军工保密资质介绍 军工保密资质是指国家对从事军工研发、生产、销售等活动的企事业单位进行的一种资质认证。该资质的核心目标是保护国家军事机密和军事技术秘密,确保国家安全和国防利益。军工保密资质的认证标准非常严格,涉及企业的安全管理、技术保密…...

ES6的编程风格
ES6 提出了两个新的声明变量的命令:let和const。其中,let完全可以取代var,因为两者语义相同,而且let没有副作用。 var命令存在变量提升效用,let命令没有这个问题 if (true) {console.log(x); // ReferenceErrorlet x…...
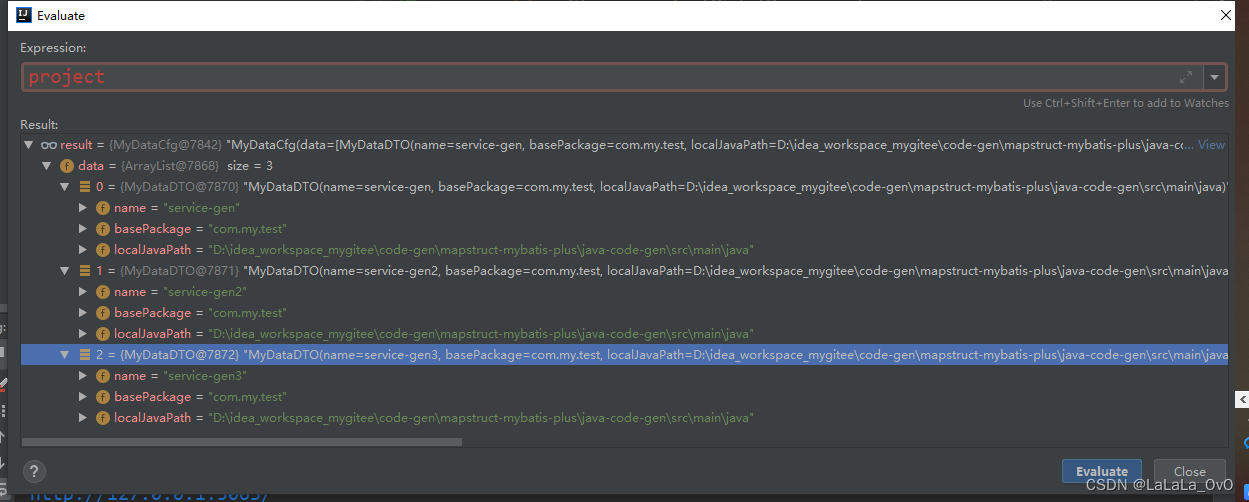
springboot 载入自定义的yml文件转DTO
json解析的pom引入 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-json</artifactId><version>5.8.20</version></dependency>resources目录下的my-data.yml project:data:- name: service-genbase-package:…...

webpack-(plugin,本地服务器,路径别名,安装vue)
安装vue npm i vue-loader -D npm i vue 编写一个vue文件: 在index.html中设置 一个id为app的div 将vue文件挂载到app中 vue比较特殊,除了使用loader外,还使用了plugin const path require("path"); const { VueLoaderPlugin …...

http请求头导致了dial tcp:lookup xxxx on 10.43.0.10:53 no sunch host
事实证明人有的时候也不能太偷懒,太偷懒容易给自己埋坑。 问题的背景: web端调用服务A,服务A异步调用服务B。服务A有四个场景需要调用服务B,所以,服务A中封装了一个公用的方法,唯一的区别是,场…...

想要设计放大电路,必须掌握哪些?
放大电路是电子系统中的核心组成部分,其设计好坏将直接影响到整个系统的性能,对电子工程师来说,在设计放大电路时,必须掌握且关注多方面,以此确保电路的稳定性和放大效果,那么需要注意哪些? 1、…...
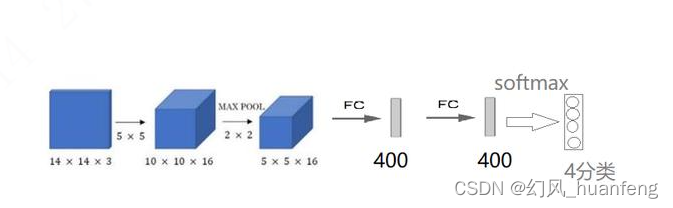
每天五分钟计算机视觉:基于卷积操作完成滑动窗口的图片分类?
本文重点 我们前面学习了使用不同大小的滑动窗口来滑动图片,然后切分成许多小的图片,然后依次应用到我们已经训练好的图像分类模型中,但是这种方式效率太低了,本节课程我们学习一种新的方式,来看一下如何并行识别这些剪切的图片。 原始结构 首先我们先来看一下,如何把…...

UI设计/交互设计/视觉设计项目汇报/作品集Figma/PPT模板
作为UI设计/交互设计/视觉设计师,创建作品集对于向潜在客户或雇主展示您的技能、创造力和风格至关重要。以下分步指南可帮助您创建令人印象深刻的作品集: 选择您的最佳作品:选择您最强大且最相关的设计项目,将其纳入您的作品集。…...
)
25、Lua 学习笔记之三(高阶话题)
Lua 学习笔记之三 高阶话题迭代实例代码有关迭代的描述 协作线程实例代码有关协作线程的描述 高阶话题 迭代 实例代码 --迭代 local function enum(array)local index 1return function()local ret array[index]index index 1return retend endlocal function foreach(a…...
企业网盘搭建——LNMP
php包链接:https://pan.baidu.com/s/1RElYTQx320pN6452N_7t1Q?pwdp8gs 提取码:p8gs 网盘源码包链接:https://pan.baidu.com/s/1BaYqwruka1P6h5wBBrLiBw?pwdwrzo 提取码:wrzo 目录 一.手动部署 二.自动部署 一.手动部署 …...

Go语言异常处理方式
Go 语言没有传统的异常处理机制,如 Java、C 或 Python 中的 try-catch 语句。取而代之,Go 采用了基于返回错误值和 panic/recover 机制的混合模式来进行错误处理。以下是 Go 语言中处理异常(或称错误)的两种主要方式: …...

时序分析基本知识点
【FPGA开发/IC开发之时序约束最全面的归纳总结】时序路径基本概念及时序约束分析方法_时序约束指令-CSDN博客...

ELK(Elasticsearch+Logstash+Kibana)日志分析系统
目录 前言 一、ELK日志分析系统概述 1、三大组件工具介绍 1.1 Elasticsearch 1.1.1 Elasticsearch概念 1.1.2 关系型数据库和ElasticSearch中的对应关系 1.1.3 Elasticsearch提供的操作命令 1.2 Logstash 1.2.1 Logstash概念 1.2.2 Logstash的主要组件 1.2.3 Logsta…...

【投稿优惠-EI稳定检索】2024年地理信息技术与遥感测绘国际学术会议(ICGITRSM 2024)
2024 International Conference on Geographic Information Technology and Remote Sensing Mapping (ICGITRSM 2024) ●会议简介 2024年地理信息技术与遥感测绘国际学术会议将聚焦于地理信息技术及遥感测绘领域的最新发展与应用。本次会议汇聚了来自世界各地的顶尖专家和学者…...

MySQL的内外连接
📟作者主页:慢热的陕西人 🌴专栏链接:MySQL 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 本博客主要内容主要介绍了MySQL中的内外连接 文章目录 MySQL的内外连接…...

Pandas连接MySQL数据库
pandas是一个强大的Python工具包,能够快速帮助我们做很多数据处理。但是在利用pandas连接数据库时,也会遇到很多问题,在此我总结了一个相对较为简单的连接范式,供大家参考学习。 先上代码: import pandas as pd# 数据…...

2024华中杯数学建模参考思路+完整代码+后续成品论文预约
(完整版资料获取在文末哦) 关于24年华中杯的更新进度,大家可以参考我们前年比赛。 22年华中杯思路: 大家也可以看这一篇 A题思路 一订单包含多种货品,每种商品有不同的数量,题目没说订单的需求时间&am…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
