C++之Eigen库基本使用
目录
1、矩阵的构造和初始化操作
2、矩阵的算术运算
3、矩阵的分解和求解
4、矩阵的变换
5、矩阵的访问和修改
6、矩阵遍历
7、线性方程组求解
8、其他操作
Eigen库是一个高级的C++库,用于线性代数,矩阵和向量运算,数值分析和相关的数学运算。这个库提供了大量的矩阵操作功能。
1、矩阵的构造和初始化操作
Eigen::Matrix3f A; // 创建一个3x3的双精度浮点型矩阵A << 1, 2, 3, 4, 5, 6, 7, 8, 9;cout<<"3X3 float: \n"<<A<<endl;Eigen::MatrixXf m = Eigen::MatrixXf::Identity(3, 3); // 创建一个3x3的单位矩阵cout<<"3X3 identity: \n"<<m<<endl;Eigen::MatrixXf mf(3, 3); // 使用构造函数初始化,默认初始化为0 Eigen::MatrixXi mi(3, 3); // 创建一个3x3的整型矩阵,默认初始化为0cout<<"3X3 mf: \n"<<mf<<endl;cout<<"3X3 mi: \n"<<mi<<endl;Eigen::MatrixXf z = Eigen::MatrixXf::Zero(3, 3); // 创建一个3x3的全0矩阵Eigen::MatrixXi n = Eigen::MatrixXi::Ones(3, 3); // 创建一个3x3的全1矩阵cout<<"3X3 Zero: \n"<<z<<endl;cout<<"3X3 Ones: \n"<<n<<endl;Eigen::MatrixXf r = Eigen::MatrixXf::Random(3, 3); // 创建一个3x3的随机矩阵cout<<"3X3 random: \n"<<r<<endl;float data[9] = {1, 2, 3, 4, 5, 6, 7, 8, 9};Eigen::Map<Eigen::MatrixXf> mp(data, 3, 3); // 将data数组映射为一个3x3的矩阵cout<<"3X3 map mp: \n"<<mp<<endl;Eigen::MatrixXf m_i(3, 3);m_i = (Eigen::MatrixXf(3, 3)<<1, 2, 3, 4, 5, 6, 7, 8, 9).finished(); //对于动态大小的矩阵,可以使用逗号初始化器,但需要在初始化时指定大小cout<<"initializer m_i: \n"<<m_i<<endl;Eigen::MatrixXf m_c = m_i;cout<<"copy constructor m_c : \n"<<m_c<<endl;2、矩阵的算术运算
Eigen::MatrixXf m1 = Eigen::MatrixXf::Identity(3, 3);Eigen::MatrixXf m2 = Eigen::MatrixXf::Identity(3, 3);Eigen::Matrix3f sum = m1 + m2; // 矩阵加法 cout<<"sum : \n"<<sum<<endl;Eigen::MatrixXf diff = m1 + m2; // 矩阵减法 cout<<"diff : \n"<<diff<<endl;Eigen::MatrixXf scaled = m1 * 2.0f; // 矩阵与标量的乘法 cout<<"scaled : \n"<<scaled<<endl;Eigen::MatrixXf product = m1 * m2.transpose(); // 矩阵乘法cout<<"product : \n"<<product<<endl;// 矩阵加法
Eigen::Matrix3f C = A + A;// 矩阵乘法
Eigen::Matrix3f D = A * A.transpose();// 向量加法
Eigen::Vector4f e = b + b;// 点积(内积)
float dotProduct = b.dot(b);// 转置
std::cout << "Transpose of A:\n" << A.transpose() << std::endl;// 访问元素
std::cout << "Element (1, 1) of A: " << A(1, 1) << std::endl;
3、矩阵的分解和求解
Eigen::MatrixXf m1 = Eigen::Matrix3f::Random();cout << "original matrix:\n" << m1 << endl;// 对矩阵进行特征值分解Eigen::EigenSolver<Eigen::Matrix3f> es(m1);cout << "eigenvalues:\n" << es.eigenvalues() << endl; cout << "eigenvectors:\n" << es.eigenvectors() << endl; // 假设我们有一个线性方程组 Ax = bEigen::Vector3f b(1, 2, 3);cout << "vector b:\n" << b << endl;// 使用列主元QR分解求解线性方程组Eigen::Vector3f x = m1.colPivHouseholderQr().solve(b);cout << "Solution x:\n" << x << endl;4、矩阵的变换
Eigen::MatrixXf m1 = Eigen::Matrix4f::Random();cout << "original matrix:\n" << m1 << endl;// 获取矩阵的转置 Eigen::Matrix4f transposed = m1.transpose();cout << "transposed:\n" << transposed << endl; // 获取矩阵的对角线元素Eigen::Vector4f diagonal = m1.diagonal();cout << "diagonal:\n" << diagonal << endl; // 获取矩阵的逆(注意:需要先检查矩阵是否可逆)if(m1.determinant() != 0) // 使用行列式检查是否可逆{// 求逆矩阵Eigen::Matrix4f inv_m = m1.inverse();cout << "inverse:\n" << inv_m << endl; // 验证逆矩阵的正确性:m * inv_m 应该接近单位矩阵Eigen::MatrixXf identity_check = m1 * inv_m;cout << "identity check:\n" << identity_check << endl; }else { cerr << "Matrix is singular and cannot be inverted." << endl; } 5、矩阵的访问和修改
Eigen::MatrixXf m1 = Eigen::Matrix4f::Random();cout << "original matrix:\n" << m1 << endl;// 取出前3行和前3列的子矩阵Eigen::Matrix3f sub_matrix = m1.block(0, 0, 3, 3);cout << "sub_matrix:\n" << sub_matrix << endl;// 修改矩阵的元素 m1(1, 2) = 10; // 将第2行第3列的元素设置为10// 访问矩阵的元素cout << "Element at (1, 2): " << m1(1, 2) << endl;// 访问矩阵的第2行 Eigen::Vector4f row = m1.row(1);cout << "row 2: " << row << std::endl;// 访问矩阵的第2列 Eigen::Vector4f col = m1.col(1);cout << "col 2: " << col << std::endl;Eigen::MatrixXf m2 = Eigen::Matrix3f::Random();cout << "original matrix:\n" << m2 << endl;// 创建一个4x4的矩阵,并初始化 Eigen::Matrix4f m4_4= Eigen::Matrix4f::Zero();// 将3x3矩阵赋值给4x4矩阵的前3行和前3列 m4_4.block(0, 0, 3, 3) = m2;cout << "4x4 matrix with 3x3 block assigned:\n" << m4_4 << endl;
//块操作
// 提取矩阵的第二列
Eigen::Vector3f column = A.col(1);// 提取矩阵的前两行
Eigen::Matrix2f topRows = A.topRows(2);
6、矩阵遍历
3.1 使用迭代器遍历和打印#include <iostream>
#include <Eigen/Dense>int main() {Eigen::MatrixXd mat(3, 4);mat << 1, 2, 3, 4,5, 6, 7, 8,9, 0, 1, 2;// 遍历并打印矩阵的每一行for (int row = 0; row < mat.rows(); ++row) {for (Eigen::MatrixXd::RowIterator it = mat.row(row).begin(); it != mat.row(row).end(); ++it) {std::cout << *it << ' ';}std::cout << '\n';}Eigen::VectorXd vec(5);vec << 3, 6, 9, 12, 15;// 遍历并打印向量的所有元素for (Eigen::VectorXd::Iterator it = vec.begin(); it != vec.end(); ++it) {std::cout << *it << ' ';}std::cout << '\n';return 0;
}3.2 直接访问元素并打印
#include <iostream>
#include <Eigen/Dense>int main() {Eigen::MatrixXd mat(3, 4);mat << 1, 2, 3, 4,5, 6, 7, 8,9, 0, 1, 2;// 遍历并打印矩阵的每一行for (int row = 0; row < mat.rows(); ++row) {for (int col = 0; col < mat.cols(); ++col) {std::cout << mat(row, col) << ' ';}std::cout << '\n';}Eigen::VectorXd vec(5);vec << 3, 6, 9, 12, 15;// 遍历并打印向量的所有元素for (int i = 0; i < vec.size(); ++i) {std::cout << vec(i) << ' ';}std::cout << '\n';return 0;
}7、线性方程组求解
// 假设A是已知的系数矩阵,b是已知的右侧向量
Eigen::VectorXd x;
Eigen::MatrixXd A(3, 3);
Eigen::VectorXd b(3);// ... 初始化A和b ...// 使用LLT分解求解Ax=b
Eigen::LLT<Eigen::MatrixXd> llt(A);
if (llt.info() == Eigen::Success) {x = llt.solve(b);
} else {std::cerr << "LLT decomposition failed!" << std::endl;
}// 输出解
std::cout << "Solution: " << x << std::endl;8、其他操作
Eigen::Matrix3f m1; // 创建一个3x3的双精度浮点型矩阵m1 << 1, 2, 3, 4, 5, 6, 7, 8, 9;// 计算矩阵的Frobenius范数float norm = m1.norm();cout << "norm of the matrix: " << norm << endl;Eigen::Matrix3f m2; // 创建一个3x3的双精度浮点型矩阵m2 << 1, 2, 3, 4, 5, 6, 7, 8, 9.0001f;// 检查两个矩阵是否近似相等(这里使用1e-5作为精度阈值)bool are_approx = m1.isApprox(m2, 1e-5);cout << "are m1 and m2 approximately equal? " << (are_approx ? "Yes" : "No") << endl;相关文章:

C++之Eigen库基本使用
目录 1、矩阵的构造和初始化操作 2、矩阵的算术运算 3、矩阵的分解和求解 4、矩阵的变换 5、矩阵的访问和修改 6、矩阵遍历 7、线性方程组求解 8、其他操作 Eigen库是一个高级的C库,用于线性代数,矩阵和向量运算,数值分析和相关的数学…...

2024年 Java 面试八股文——SpringBoot篇
目录 1. 什么是 Spring Boot? 2. 为什么要用SpringBoot 3. SpringBoot与SpringCloud 区别 4. Spring Boot 有哪些优点? 5. Spring Boot 的核心注解是哪个?它主要由哪几个注解组成的? 6. Spring Boot 支持哪些日志框架&#…...

C/C++的指针、万能指针、常量指针和指针常量
C/C的指针 1、 指针的概念: 指针是一个变量,它存储的是另一个变量的内存地址,而不是变量的值。 指针变量的声明:在C/C等语言中,我们通过使用星号*来声明一个指针变量。例如,int *ptr; 这行代码声明了一个…...

【讲解下如何解决一些常见的 Composer 错误】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...

qq空间:图片批量下载js脚本工具,javascript批量下载图片
qq空间:图片批量下载js脚本工具,javascript批量下载图片 QQ空间很多老照片想下载,但是腾讯没放开,只能一张张下载太麻烦。用前端js写了一个脚本支持批量下载。另外就是空间内的照片会被压缩,过几年再看,个…...

滑动验证码登陆测试编程示例
一、背景及原理 处理登录时的滑动验证码有两个难点,第一个是找到滑块需要移动的距离,第二个是模拟人手工拖动的轨迹。模拟轨迹在要求不是很严的情况下可以用先加速再减速拖动的方法,即路程的前半段加速度为正值,后半段为负值去模…...

爬取89ip代理、 爬取豆瓣电影
1 爬取89ip代理 2 爬取豆瓣电影 1 爬取89ip代理 import requests from fake_useragent import UserAgent from bs4 import BeautifulSoup from requests.exceptions import ProxyErrorclass SpiderIP:def __init__(self):# 定义目标地址哦self.tag_url "https://www.89i…...

XBoot:基于Spring Boot 2.x的一站式前后端分离快速开发平台
XBoot:基于Spring Boot 2.x的一站式前后端分离快速开发平台 摘要 随着信息技术的迅速发展,快速构建高质量、高可靠性的企业级应用成为了迫切需求。XBoot,作为一个基于Spring Boot 2.x的一站式前后端分离快速开发平台,通过整合微信…...

24年最新抖音、视频号0成本挂机,单号每天收益上百,可无限挂
详情介绍 这次给大家带来5月份最新的短视频挂机项目,简单易上手,而且不需要任何投入,经过测试收益非常可观,软件完全免费,特别适合没有时间但是想做副业的家人们...

Day31:单元测试、项目监控、项目部署、项目总结、常见面试题
单元测试 保证独立性。 Assert:断言,一般用来比较是否相等,比如 Assert.assertEquals 在JUnit测试框架中,BeforeClass,Before,After和AfterClass是四个常用的注解,它们的作用如下: …...

Flutter笔记:使用Flutter私有类涉及的授权协议问题
Flutter笔记 使用Flutter私有类涉及的授权协议问题 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.cs…...

面试过程种遇到的面试题收集
文章目录 讲一讲这个项目是干什么的?需求规格说明书有哪些章节?职工部门层级如何显示在一张SQL表上?需求开发用到了哪些技术?HashMap 底层数据结构说一下?介绍一下红黑树?HashMap是线程不安全的,…...

Vue学习:21.mixins混入
在Vue中,mixins(混入)是一种用于分发Vue组件中可复用功能的灵活机制。它们允许你抽取组件中的共享功能,如数据、计算属性、方法、生命周期钩子等,并将其作为单独的模块复用到多个组件中。这种方式有助于保持代码的DRY&…...
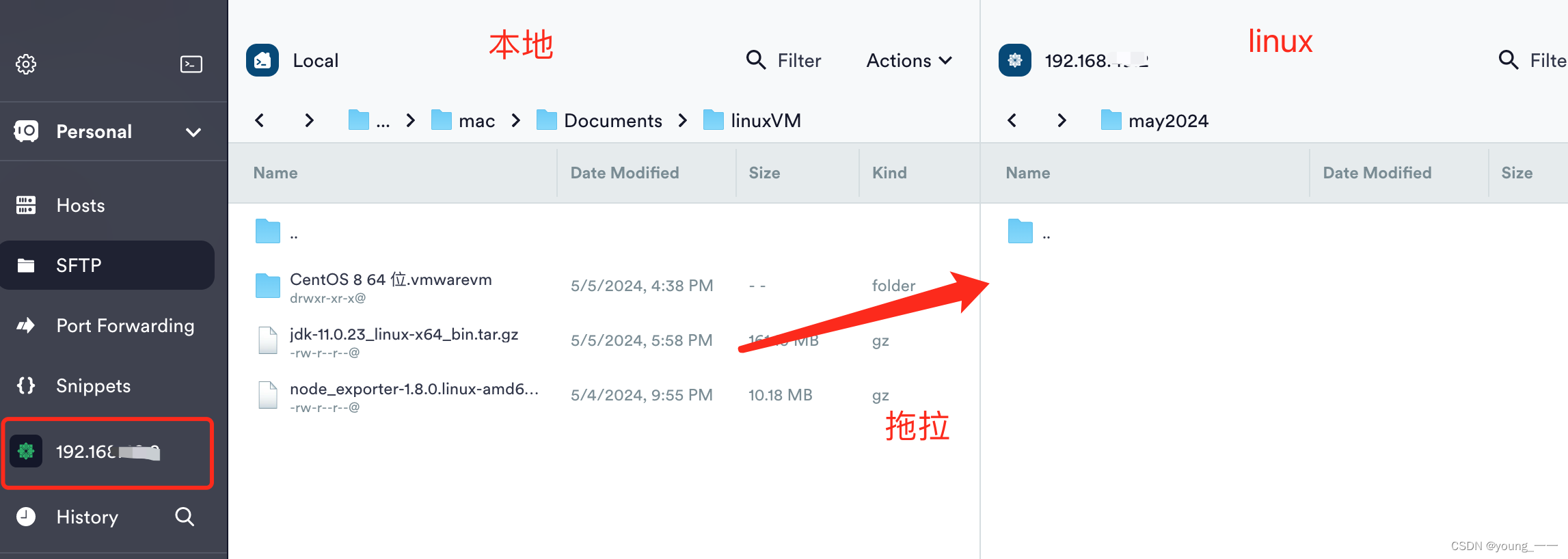
上传文件到 linux
一、mac 法一:scp 先进入mac的 Node_exporter文件(要上传的文件)目录下 输入scp -P 端口号 文件名 rootIP:/存放路径 scp -P 22 node_exporter-1.8.0.linux-amd64.tar.gz root192.***.2:/root 法二、 rz mac 安装 lrzsz,然后…...

NEO 学习之session7
文章目录 选项 A:它涉及学习标记数据。 选项 B:它需要预定义的输出标签进行训练。 选项 C:它涉及在未标记的数据中寻找模式和关系。 选项 D:它专注于根据输入-输出对进行预测。 答案:选项 C 描述了无监督学习的本质&am…...
毕业设计uniapp+vue有机农产品商城系统 销售统计图 微信小程序
本人在网上找了一下这方面的数据发现农村中的信心普及率很是低农民们都不是怎么会用手机顶多就是打打电话发发短信,平时不太会上网更不会想到通过网络手段去卖出自己的劳作成果—农产品,这无疑大大浪费了农民的劳动成果和国家资源也大大打击了人们的生产…...
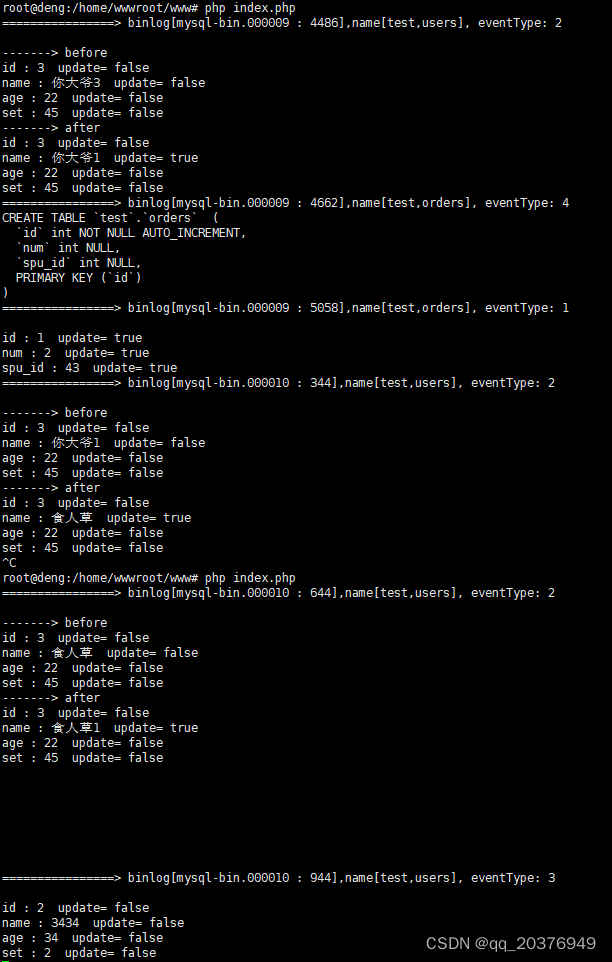
php使用Canal监听msyql
canal需要java8 去官网下载java8 安装JAVA #创建目录 mkdir -p /usr/local/java/ #解压到目录 tar zxvf jdk-8u411-linux-x64.tar.gz -C /usr/local/java/配置环境变量在 /etc/profile 最后加入 export JAVA_HOME/usr/local/java/jdk1.8.0_411 export CLASSPATH.:$JAVA_HOM…...
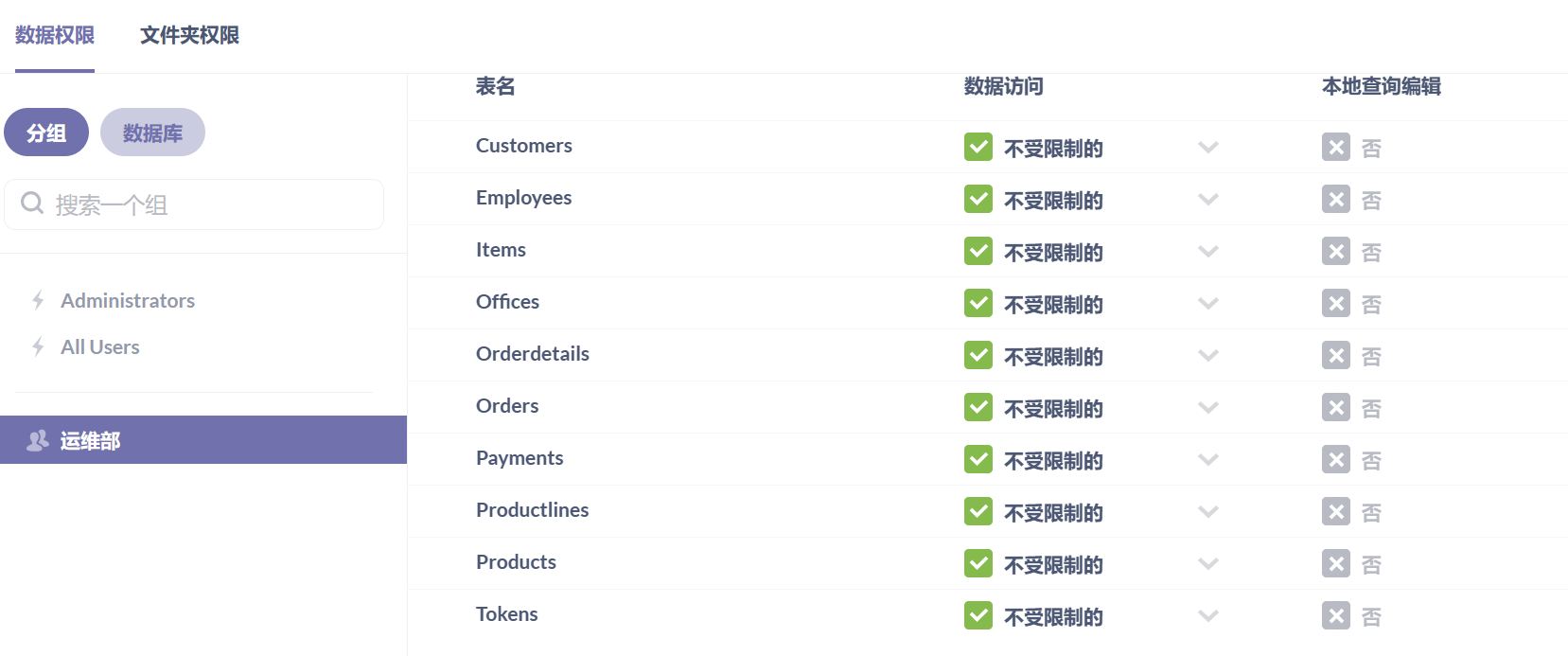
metabase部署与实践
1. 项目目标 (1)了解metabase特点 (2)熟练部署metabase工具 (3)掌握metabase基本使用 2. 项目准备 2.1. 规划节点 主机名 主机IP 节点规划 metabase 10.0.1.141 metabase 2.2. 基础准备 系统镜…...

nacos v2.2.3 docker简单安装使用
nacos v2.2.3 docker简单安装使用 Nacos 官方文档: https://nacos.io/zh-cn/docs/v2/quickstart/quick-start.html 控制台: http://127.0.0.1:8848/nacos/ 初始用户名、密码: 账号:nacos 密码:nacos 启动docker…...

java设计模式-生成器模式
文章目录 生成器模式(Builder)1、目的和适用场景2、角色和职责3、实现步骤4、示例15、示例26、优点7、示例场景 生成器模式(Builder) 生成器模式(Builder Pattern)是一种创建型设计模式,它用于…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...

[特殊字符] Spring Boot底层原理深度解析与高级面试题精析
一、Spring Boot底层原理详解 Spring Boot的核心设计哲学是约定优于配置和自动装配,通过简化传统Spring应用的初始化和配置流程,显著提升开发效率。其底层原理可拆解为以下核心机制: 自动装配(Auto-Configuration) 核…...

Gitlab + Jenkins 实现 CICD
CICD 是持续集成(Continuous Integration, CI)和持续交付/部署(Continuous Delivery/Deployment, CD)的缩写,是现代软件开发中的一种自动化流程实践。下面介绍 Web 项目如何在代码提交到 Gitlab 后,自动发布…...
【JavaEE】万字详解HTTP协议
HTTP是什么?-----互联网的“快递小哥” 想象我们正在网上购物:打开淘宝APP,搜索“蓝牙耳机”,点击商品图片,然后下单付款。这一系列操作背后,其实有一个看不见的“快递小哥”在帮我们传递信息,…...
