强化学习:时序差分法【Temporal Difference Methods】
强化学习笔记
主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程,个人觉得赵老师的课件深入浅出,很适合入门.
第一章 强化学习基本概念
第二章 贝尔曼方程
第三章 贝尔曼最优方程
第四章 值迭代和策略迭代
第五章 强化学习实例分析:GridWorld
第六章 蒙特卡洛方法
第七章 Robbins-Monro算法
第八章 多臂老虎机
第九章 强化学习实例分析:CartPole
文章目录
- 强化学习笔记
- 一、on-policy vs off-policy
- 二、TD learning of state values
- 1 迭代格式
- 2 推导
- 3 分析
- 4 TD(0)与蒙特卡洛方法的对比
- 三、Sarsa
- 四、Expected Sarsa
- 五、Q-learning
- 六、参考资料
在强化学习实例分析:CartPole中,我们通过实验发现了蒙特卡洛方法的一些缺点:
- 每次更新需要等到一个episode结束;
- 越到后面的episode,耗时越长,效率低.
本节介绍强化学习中经典的时序差分方法(Temporal Difference Methods,TD)。与蒙特卡洛(MC)学习类似,TD学习也是Model-free的,但由于其增量形式在效率上相较于MC方法具有一定的优势。
一、on-policy vs off-policy
在介绍时序差分算法之前,首先介绍一下on-policy 和 off-policy的概念:
- On-policy:我们把用于产生采样样本的策略称为behavior-policy,在policy-improvement步骤进行改进的策略称为target-policy.如果这两个策略相同,我们称之为On-policy算法。
- Off-policy:如果behavior-policy和target-policy不同,我们称之为Off-policy算法。
比如在Monte-Carlo算法中,我可以用一个给定策略 π a \pi_a πa来产生样本,这个策略可以是 ϵ \epsilon ϵ-greedy策略,以保证能够访问所有的 s s s和 a a a。而我们目标策略可以是greedy策略 π b \pi_b πb,在policy-imporvement阶段我们不断改进 π b \pi_b πb,最终得到一个最优的策略。这样我们最后得到的最优策略 π b ∗ \pi_b^* πb∗就是一个贪婪策略,不用去探索不是最优的动作,这样我们用 π b ∗ \pi_b^* πb∗可以得到更高的回报。
二、TD learning of state values
1 迭代格式
和蒙特卡洛方法一样,用TD learning来估计状态值 v ( s ) v(s) v(s),我们也需要采样的数据,假设给定策略 π \pi π,某个episode采样得到的序列如下:
( s 0 , r 1 , s 1 , . . . , s t , r t + 1 , s t + 1 , . . . ) (s_0, r_1, s_1, . . . , s_t , r_{t+1}, s_{t+1}, . . .) (s0,r1,s1,...,st,rt+1,st+1,...)
那么TD learning给出在第 t t t步状态值 v ( s ) v(s) v(s)的更新如下:
v ( s t ) = v ( s t ) + α t ( s t ) [ r t + 1 + γ v ( s t + 1 ) − v ( s t ) ] ( 1 ) v(s_t)=v(s_t)+\alpha_t(s_t)[r_{t+1}+\gamma v(s_{t+1})-v(s_t)]\qquad(1) v(st)=v(st)+αt(st)[rt+1+γv(st+1)−v(st)](1)
Note:
- s t s_t st是当前状态, s t + 1 s_{t+1} st+1是跳转到的下一个状态,这里需要用到 v ( s t + 1 ) v(s_{t+1}) v(st+1)(本身也是一个估计值);
- 我们可以看到,TD方法在每个时间步都会进行更新,不需要得到整个episode结束才更新;
- 这个算法被称为TD(0)。
当 a t ( s t ) a_t(s_t) at(st)取常量 α \alpha α时,下面给出 v π ( s ) v_{\pi}(s) vπ(s)估计的伪代码:

2 推导
TD(0)的迭代格式为什么是这样的呢?和前面介绍随机近似中的RM算法似乎有点像,事实上它可以看作是求解Bellman方程的一种特殊的随机近似算法。我们回顾贝尔曼方程中介绍的:
v π ( s ) = E [ G t ∣ S t = s ] = E [ R t + γ G t + 1 ∣ S t = s ] = E [ R t + γ v π ( S t + 1 ) ∣ S t = s ] ( 2 ) \begin{aligned} v_{\pi}(s)&=\mathbb{E}[G_t|S_t=s]\\ &=\mathbb{E}[R_t+\gamma G_{t+1}|S_t=s]\\ &=\mathbb{E}[R_t+\gamma v_{\pi}(S_{t+1})|S_t=s]\\ \end{aligned} \qquad(2) vπ(s)=E[Gt∣St=s]=E[Rt+γGt+1∣St=s]=E[Rt+γvπ(St+1)∣St=s](2)
下面我们用Robbins-Monro算法来求解方程(2),对于状态$s_t, $,我们定义一个函数为
g ( v π ( s t ) ) ≐ v π ( s t ) − E [ R t + 1 + γ v π ( S t + 1 ) ∣ S t = s t ] . g(v_\pi(s_t))\doteq v_\pi(s_t)-\mathbb{E}\big[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s_t\big]. g(vπ(st))≐vπ(st)−E[Rt+1+γvπ(St+1)∣St=st].
那么方程(2)等价于
g ( v π ( s t ) ) = 0. g(v_\pi(s_t))=0. g(vπ(st))=0.
显然我们可以用RM算法来求解上述方程的根,就能得到 v π ( s t ) v_{\pi}(s_t) vπ(st)。因为我们可以通过采样获得 r t + 1 r_{t+1} rt+1和 s t + 1 s_{t+1} st+1,它们是 R t + 1 R_{t+1} Rt+1和 S t + 1 S_{t+ 1} St+1的样本,我们可以获得的$g( v_\pi ( s_{t}) ) $的噪声观测是
g ~ ( v π ( s t ) ) = v π ( s t ) − [ r t + 1 + γ v π ( s t + 1 ) ] = ( v π ( s t ) − E [ R t + 1 + γ v π ( S t + 1 ) ∣ S t = s t ] ) ⏟ g ( v π ( s t ) ) + ( E [ R t + 1 + γ v π ( S t + 1 ) ∣ S t = s t ] − [ r t + 1 + γ v π ( s t + 1 ) ] ) ⏟ η . \begin{aligned}\tilde{g}(v_{\pi}(s_{t}))&=v_\pi(s_t)-\begin{bmatrix}r_{t+1}+\gamma v_\pi(s_{t+1})\end{bmatrix}\\&=\underbrace{\left(v_\pi(s_t)-\mathbb{E}\big[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s_t\big]\right)}_{g(v_\pi(s_t))}\\&+\underbrace{\left(\mathbb{E}\big[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s_t\big]-\big[r_{t+1}+\gamma v_\pi(s_{t+1})\big]\right)}_{\eta}.\end{aligned} g~(vπ(st))=vπ(st)−[rt+1+γvπ(st+1)]=g(vπ(st)) (vπ(st)−E[Rt+1+γvπ(St+1)∣St=st])+η (E[Rt+1+γvπ(St+1)∣St=st]−[rt+1+γvπ(st+1)]).
因此,求解 g ( v π ( s t ) ) = 0 g(v_{\pi}(s_{t}))=0 g(vπ(st))=0的RM算法为
v t + 1 ( s t ) = v t ( s t ) − α t ( s t ) g ~ ( v t ( s t ) ) = v t ( s t ) − α t ( s t ) ( v t ( s t ) − [ r t + 1 + γ v π ( s t + 1 ) ] ) , ( 3 ) \begin{aligned}v_{t+1}(s_{t})&=v_t(s_t)-\alpha_t(s_t)\tilde{g}(v_t(s_t))\\&=v_t(s_t)-\alpha_t(s_t)\Big(v_t(s_t)-\big[r_{t+1}+\gamma v_\pi(s_{t+1})\big]\Big),\end{aligned}\qquad(3) vt+1(st)=vt(st)−αt(st)g~(vt(st))=vt(st)−αt(st)(vt(st)−[rt+1+γvπ(st+1)]),(3)
其中 v t ( s t ) v_t(s_t) vt(st)是 v π ( s t ) v_\pi(s_t) vπ(st)在$t, 时间点的估计, 时间点的估计, 时间点的估计,\alpha _t( s_t) $是学习率。
Note:
- (3)中的算法与(1)中的TD(0)具有相似的表达式,唯一的区别是(3)的右侧包含 v π ( s t + 1 ) v_{\pi}(s_{t+1}) vπ(st+1),而(1)包含 v t ( s t + 1 ) v_t(s_{t+1}) vt(st+1),这是因为(3)的设计是通过假设其他状态值已知来估计 s t s_t st的动作值。
- 如果我们想估计所有状态的状态值,则右侧的 v π ( s t + 1 ) v_{\pi}(s_{t+1}) vπ(st+1)应替换为 v t ( s t + 1 ) v_t(s_{t+1}) vt(st+1),那么(3)与(1)完全相同。并且我们可以证明这样的替换能保证所有 v t ( s ) v_t(s) vt(s)都收敛到 v π ( s ) v_{\pi}(s) vπ(s),这里就不再展开。
3 分析
我们再来看一下TD(0)的迭代格式:
v t + 1 ( s t ) ⏟ new estimate = v t ( s t ) ⏟ current estimate − α t ( s t ) [ v t ( s t ) − ( r t + 1 + γ v t ( s t + 1 ) ⏟ TD target v ˉ t ) ⏞ TD error δ t ] , ( 4 ) \underbrace{v_{t+1}(s_t)}_{\text{new estimate}}=\underbrace{v_t(s_t)}_{\text{current estimate}}-\alpha_t(s_t)\Big[\overbrace{v_t(s_t)-\Big(\underbrace{r_{t+1}+\gamma v_t(s_{t+1})}_{\text{TD target }\bar{v}_t}\Big)}^{\text{TD error }\delta_t}\Big],\qquad (4) new estimate vt+1(st)=current estimate vt(st)−αt(st)[vt(st)−(TD target vˉt rt+1+γvt(st+1)) TD error δt],(4)
其中
v ˉ t ≐ r t + 1 + γ v t ( s t + 1 ) ( 5 ) \bar{v}_t\doteq r_{t+1}+\gamma v_t(s_{t+1})\qquad(5) vˉt≐rt+1+γvt(st+1)(5)
被称为TD target,
δ t ≐ v ( s t ) − v ˉ t = v t ( s t ) − ( r t + 1 + γ v t ( s t + 1 ) ) ( 6 ) \delta_t\doteq v(s_t)-\bar{v}_t=v_t(s_t)-(r_{t+1}+\gamma v_t(s_{t+1}))\qquad(6) δt≐v(st)−vˉt=vt(st)−(rt+1+γvt(st+1))(6)
被称为TD-error.
为什么(5)被称为TD target,因为迭代格式(4)是让 v t + 1 v_{t+1} vt+1朝着 v ˉ t \bar{v}_t vˉt更新的,我们考察:
∣ v t + 1 ( s t ) − v ˉ t ∣ = ∣ [ v t ( s t ) − v ˉ t ] − α t ( s t ) [ v t ( s t ) − v ˉ t ] ∣ = ∣ [ 1 − α t ( s t ) ] ∣ ∣ [ v t ( s t ) − v ˉ t ] ∣ ≤ ∣ [ v t ( s t ) − v ˉ t ] ∣ \begin{aligned} |v_{t+1}(s_t)-\bar{v}_t|&=|\begin{bmatrix}v_t(s_t)-\bar{v}_t\end{bmatrix}-\alpha_t(s_t)\big[v_t(s_t)-\bar{v}_t\big]|\\ &=|[1-\alpha_t(s_t)]||\big[v_t(s_t)-\bar{v}_t\big]|\\ &\leq|\big[v_t(s_t)-\bar{v}_t\big]| \end{aligned} ∣vt+1(st)−vˉt∣=∣[vt(st)−vˉt]−αt(st)[vt(st)−vˉt]∣=∣[1−αt(st)]∣∣[vt(st)−vˉt]∣≤∣[vt(st)−vˉt]∣
显然当 0 < α t ( s t ) < 2 0<\alpha_t(s_t)<2 0<αt(st)<2时,上式的不等式成立,这意味着 v t + 1 v_{t+1} vt+1比 v t v_t vt离 v ˉ t \bar{v}_t vˉt更近,所以 v ˉ t \bar{v}_t vˉt被称为TD target。
TD-error则衡量了在 t t t时间步估计值 v t v_t vt与 v ˉ t \bar{v}_t vˉt 的差异,显然我们可以想象当 v t v_t vt估计值是准确的 v π v_{\pi} vπ时,TD-error的期望值应该为0,事实上确实如此:
E [ δ t ∣ S t = s t ] = E [ v π ( S t ) − ( R t + 1 + γ v π ( S t + 1 ) ) ∣ S t = s t ] = v π ( s t ) − E [ R t + 1 + γ v π ( S t + 1 ) ∣ S t = s t ] = v π ( s t ) − v π ( s t ) = 0. \begin{aligned} \mathbb{E}[\delta_t|S_t=s_t]& =\mathbb{E}\big[v_\pi(S_t)-(R_{t+1}+\gamma v_\pi(S_{t+1}))|S_t=s_t\big] \\ &=v_\pi(s_t)-\mathbb{E}\big[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s_t\big] \\ &=v_\pi(s_t)-v_\pi(s_t)\\ &=0. \end{aligned} E[δt∣St=st]=E[vπ(St)−(Rt+1+γvπ(St+1))∣St=st]=vπ(st)−E[Rt+1+γvπ(St+1)∣St=st]=vπ(st)−vπ(st)=0.
当TD-error趋于0时, 那么(1)也得到不到什么新的信息了,迭代也就收敛了。
4 TD(0)与蒙特卡洛方法的对比
| TD learning | Monte Carlo Methods |
|---|---|
| TD learning每得到一个样本就能更新 v ( s ) v(s) v(s)或者 q ( s , a ) q(s,a) q(s,a),这种算法被称为online的. | MC每次更新必须等到一个epsisode结束,这种算法被称为offline的. |
| TD可以处理连续性任务和episodic任务. | MC只能处理episodic任务. |
| TD被称为bootstraping方法,因为 v ( s ) v(s) v(s)/ q ( s , a ) q(s,a) q(s,a)动作的更新依赖于其他状态值先前的估计值.因此,TD需要给定一个初始值. | MC是Non-Bootstraping的. |
三、Sarsa
如果我们要得到最优策略,无论是用策略迭代还是值迭代算法,我们都需要 q ( s , a ) q(s,a) q(s,a),所以我们可以用TD learning直接来估计 q ( s , a ) q(s,a) q(s,a),给定策略 π \pi π,假设某个episode采样得到如下序列:
( s 0 , a 0 , r 1 , s 1 , a 1 , . . . , s t , a t , r t + 1 , s t + 1 , a t + 1 , . . . ) . (s_0, a_0, r_1, s_1, a_1, . . . , s_t , a_t , r_{t+1}, s_{t+1}, a_{t+1}, . . .). (s0,a0,r1,s1,a1,...,st,at,rt+1,st+1,at+1,...).
那么TD learning对 q ( s , a ) q(s,a) q(s,a)的估计如下:
q t + 1 ( s t , a t ) = q t ( s t , a t ) − α t ( s t , a t ) [ q t ( s t , a t ) − ( r t + 1 + γ q t ( s t + 1 , a t + 1 ) ) ] , ( 7 ) q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha_t(s_t,a_t)\Big[q_t(s_t,a_t)-(r_{t+1}+\gamma q_t(s_{t+1},a_{t+1}))\Big],\qquad(7) qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γqt(st+1,at+1))],(7)
Note:
- 和对状态值的估计(1)对比,我们发现(7)就是把(1)中的 v ( s ) v(s) v(s)替换为 q ( s , a ) q(s,a) q(s,a),其实就是用RM算法求解关于 q ( s , a ) q(s,a) q(s,a)的贝尔曼方程,所以得到的迭代格式类似.
- 其中 s t + 1 s_{t+1} st+1为转移的下一个状态, a t + 1 a_{t+1} at+1是在状态 s t + 1 s_{t+1} st+1下采取的动作,这里是根据策略 π \pi π得到.(因为我们采样的序列就是根据 π \pi π得到的)
- 所以如果 s t + 1 s_{t+1} st+1是终止状态,显然就没有 a t + 1 a_{t+1} at+1,此时我们定义 q ( s t + 1 , a t + 1 ) = 0 q(s_{t+1},a_{t+1})=0 q(st+1,at+1)=0.
- 这个算法每次更新会用到 ( s t , a t , r t + 1 , s t + 1 , a t + 1 ) (s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1}) (st,at,rt+1,st+1,at+1)(SARSA),所以这个算法被称为
SARSA. - 当我们有 q ( s , a ) q(s,a) q(s,a)的估计值后,我们可以使用greedy或者 ε \varepsilon ε-greedy来更新策略。可以证明如果步长 a t ( s t , a t ) a_t(s_t,a_t) at(st,at)满足RM算法收敛的条件要求,只要所有的状态-动作对被访问无限次,Sarsa以概率1收敛到最优的策略 π ∗ \pi^* π∗和最优的动作-价值函数 q ∗ ( s , a ) q^*(s,a) q∗(s,a).
同TD(0)类似,Sarsa可以看作是用RM算法求解如下贝尔曼方程得到的迭代格式:
q π ( s , a ) = E [ R + γ q π ( S ′ , A ′ ) ∣ s , a ] , for all ( s , a ) . q_\pi(s,a)=\mathbb{E}\left[R+\gamma q_\pi(S',A')|s,a\right],\quad\text{for all }(s,a). qπ(s,a)=E[R+γqπ(S′,A′)∣s,a],for all (s,a).
下面给出Sarsa完整的伪代码:

Sarsa是一种on-policy算法,因为在估计 q t q_t qt值时,会用到依据 π t \pi_t πt产生的样本,更新 q t q_t qt后,我们又会依据新的 q t q_t qt来更新策略得到 π t + 1 \pi_{t+1} πt+1,然后用 π t + 1 \pi_{t+1} πt+1产生样本继续更新 q t + 1 q_{t+1} qt+1,这样交替进行,最后得到最优策略。在这个过程中我们发现产生样本的策略和得到的最优策略是同一个策略,所以是on-policy算法。
四、Expected Sarsa
给定策略 π \pi π,其动作值可以用Sarsa的一种变体Expected-Sarsa来估计。Expected-Sarsa的迭代格式如下:
q t + 1 ( s t , a t ) = q t ( s t , a t ) − α t ( s t , a t ) [ q t ( s t , a t ) − ( r t + 1 + γ E [ q t ( s t + 1 , A ) ] ) ] = q t ( s t , a t ) − α t ( s t , a t ) [ q t ( s t , a t ) − ( r t + 1 + γ ∑ a π ( a ∣ s t + 1 ) q t ( s t + 1 ) , a ) ] \begin{aligned} q_{t+1}(s_t,a_t)&=q_t(s_t,a_t)-\alpha_t(s_t,a_t)\Big[q_t(s_t,a_t)-(r_{t+1}+\gamma\mathbb{E}[q_t(s_{t+1},A)])\Big]\\ &=q_t(s_t,a_t)-\alpha_t(s_t,a_t)\Big[q_t(s_t,a_t)-(r_{t+1}+\gamma\sum_a\pi(a|s_{t+1})q_t(s_{t+1}),a)\Big] \end{aligned} qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γE[qt(st+1,A)])]=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γa∑π(a∣st+1)qt(st+1),a)]
同Sarsa类似,Expected-Sarsa可以看作是用RM算法求解如下贝尔曼方程得到的迭代格式:
q π ( s , a ) = E [ R t + 1 + γ E [ q π ( S t + 1 , A t + 1 ) ∣ S t + 1 ] ∣ S t = s , A t = a ] = E [ R t + 1 + γ v π ( S t + 1 ) ∣ S t = s , A t = a ] . \begin{aligned} q_\pi(s,a)&=\mathbb{E}\Big[R_{t+1}+\gamma\mathbb{E}[q_\pi(S_{t+1},A_{t+1})|S_{t+1}]\Big|S_t=s,A_t=a\Big]\\ &=\mathbb{E}\Big[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s,A_t=a\Big]. \end{aligned} qπ(s,a)=E[Rt+1+γE[qπ(St+1,At+1)∣St+1] St=s,At=a]=E[Rt+1+γvπ(St+1)∣St=s,At=a].
虽然Expected Sarsa的计算复杂度比Sarsa高,但它消除了随机选择 a t + 1 a_{t+1} at+1所带来的方差。在相同的采样样本条件下,Expected Sarsa的表现通常比Sarsa更好。
五、Q-learning
接下来我们介绍强化学习中经典的Q-learning算法,Sarsa算法和Expected-Sarsa都是估计 q ( s , a ) q(s,a) q(s,a),如果我们想要得到最优策略还需要policy-improvement,而Q-learning算法则是直接估计 q ∗ ( s , a ) q^*(s,a) q∗(s,a),如果我们能得到 q ∗ ( s , a ) q^*(s,a) q∗(s,a)就不用每一步还执行policy-improvement了。Q-learning的迭代格式如下:
q t + 1 ( s t , a t ) = q t ( s t , a t ) − α t ( s t , a t ) [ q t ( s t , a t ) − ( r t + 1 + γ max a ∈ A ( s t + 1 ) q t ( s t + 1 , a ) ) ] , ( 7.18 ) q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha_t(s_t,a_t)\left[q_t(s_t,a_t)-\left(r_{t+1}+\gamma\max_{a\in\mathcal{A}(s_{t+1})}q_t(s_{t+1},a)\right)\right],\quad(7.18) qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−(rt+1+γa∈A(st+1)maxqt(st+1,a))],(7.18)
Q-learning也是一种随机近似算法,用于求解以下方程:
q ( s , a ) = E [ R t + 1 + γ max a q ( S t + 1 , a ) ∣ S t = s , A t = a ] . q(s,a)=\mathbb{E}\left[R_{t+1}+\gamma\max_aq(S_{t+1},a)\Big|S_t=s,A_t=a\right]. q(s,a)=E[Rt+1+γamaxq(St+1,a) St=s,At=a].
这是 q ( s , a ) q(s,a) q(s,a)贝尔曼最优方程,所以Q-learning本质就是求解贝尔曼最优方程的随机近似算法,其伪代码如下:

显然Q-learning是一种Off-policy算法,因为 q t ( s , a ) q_t(s,a) qt(s,a)在更新的时候,用的数据可以是一个给定 ϵ \epsilon ϵ-greedy策略 π a \pi_a πa产生的,但是直接学习到 q ∗ ( s , a ) q^*(s,a) q∗(s,a),我们可以通过 q ∗ ( s , a ) q^*(s,a) q∗(s,a)得到一个greedy策略 π b ∗ \pi_b^* πb∗.
即使Q-learning是off-policy的,但我们也可以按on-policy的方式来实现,下面给出这两种实现,我们可以更清楚地看到off-policy和on-policy的区别:


六、参考资料
- Zhao, S… Mathematical Foundations of Reinforcement Learning. Springer Nature Press and Tsinghua University Press.
- Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 2018.
相关文章:

强化学习:时序差分法【Temporal Difference Methods】
强化学习笔记 主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程,个人觉得赵老师的课件深入浅出,很适合入门. 第一章 强化学习基本概念 第二章 贝尔曼方程 第三章 贝尔曼最优方程 第四章 值迭代和策略迭代 第五章 强化学习实例分析:GridWorld…...
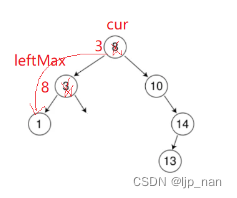
数据结构-二叉树-二叉搜索树
一、概念 二叉搜索树又称二叉排序树,它或者是一棵空树,或者具有以下性质的二叉树: 若它的左子树不为空,则左树上所有节点的值都小于根节点的值。 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值。 它…...

Linux 磁盘管理命令df du dd
文章目录 3.Linux 磁盘管理命令3.1 df:显示报告文件系统磁盘使用信息案例练习 3.2 du:显示目录或者文件所占的磁盘空间案例练习 3.3 dd:磁盘操作案例练习 3.Linux 磁盘管理命令 3.1 df:显示报告文件系统磁盘使用信息 作用&#x…...

Leetcode 3138. Minimum Length of Anagram Concatenation
Leetcode 3138. Minimum Length of Anagram Concatenation 1. 解题思路2. 代码实现 题目链接:3138. Minimum Length of Anagram Concatenation 1. 解题思路 这一题的话我们首先统计出来所有的字母出现的频率。 然后,我们只需要从头开始重新计数一下&…...
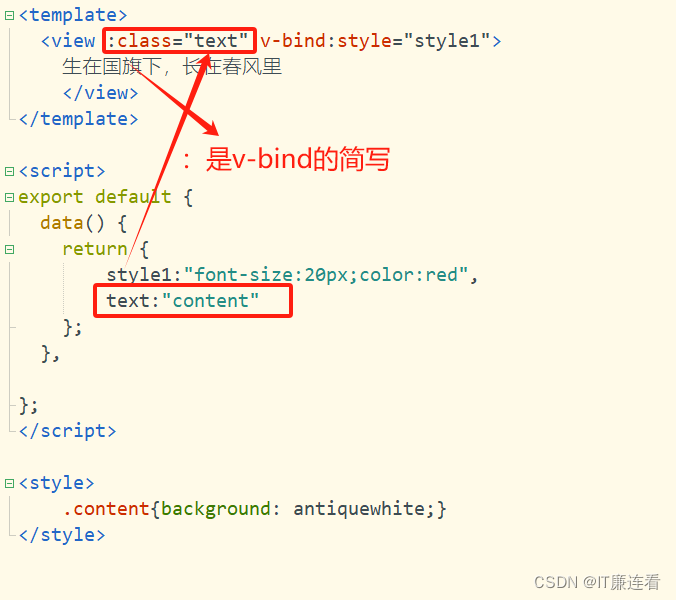
IT廉连看——UniApp——样式绑定
IT廉连看——UniApp——样式绑定 一、样式绑定 两种添加样式的方法: 1、第一种写法 写一个class属性,然后将css样式写在style中。 2、第二种写法 直接把style写在class后面 添加一些效果:字体大小 查看效果 证明这样添加样式是没有问题的…...

垃圾的flinkcdc
在 MySQL 中,创建表时使用反引号 将表名或字段名括起来的作用是: 保留字和关键字: 使用反引号可以避免使用MySQL的保留字和关键字作为表名或字段名时产生的冲突。比如,你可以创建一个名为 select 或 order 的表: sqlCopy Code C…...

关于视频号小店,常见问题解答,开店做店各方面详解
大家好,我是电商笨笨熊 视频号小店作为今年风口,一个新推出的项目,凭借着自身流量加用户群体的优势吸引了不少的电商玩家。 但对于很多玩家来说,视频号小店完全是一个新的项目、新的领域,因此也会存在很多的疑问&…...
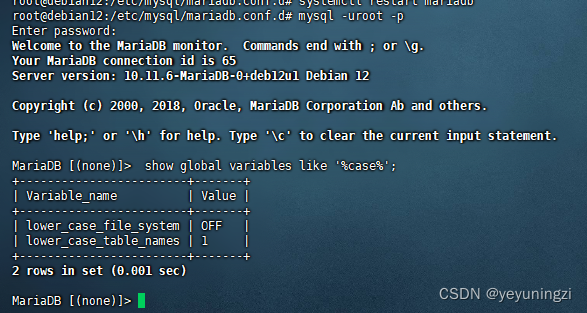
Debian mariadb 10.11设定表名 大小写不敏感方法
目录 问题表现:应用中查询 表提示 表不存在 处理步骤: 1、查询表名大小写敏感情况: show global variables like %case%; 2、修改mariadb 配置设置大小写 不敏感 mysql 配置大小写不敏感 mariadb 10.11设置表名大小写不敏感 /etc/mysq…...
常用六大加密软件排行榜|好用加密文件软件分享
为了保障数据安全,越来越多的企业开始使用文件加密软件。哪款加密软件适合企业哪些办公场景呢? 今天就给大家推荐一下文件加密软件排行榜的前六名: 1.域智盾 这款软件专为企业和政府机构设计,提供全面的文件保护解决方案。 点…...

百川2模型解读
简介 Baichuan 2是多语言大模型,目前开源了70亿和130亿参数规模的模型。在公开基准如MMLU、CMMLU、GSM8K和HumanEval上的评测,Baichuan 2达到或超过了其他同类开源模型,并在医学和法律等垂直领域表现优异。此外,官方还发布所有预…...
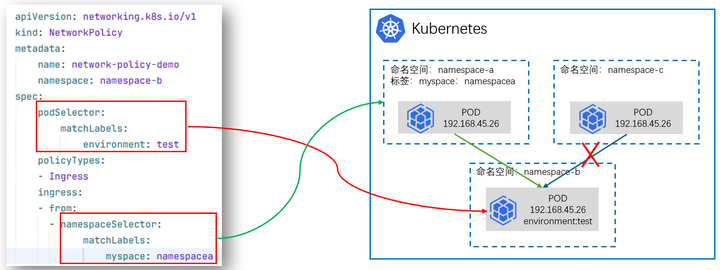
云原生专栏丨基于K8s集群网络策略的应用访问控制技术
在当今云计算时代,Kubernetes已经成为容器编排的事实标准,它为容器化应用提供了强大的自动化部署、扩展和管理能力。在Kubernetes集群中,网络策略(Network Policy)作为对Pod间通信进行控制的关键功能,对保障应用安全和隔离性起到了…...

MySQL 优化 - index_merge 导致查询偶发变慢
文章目录 前言问题描述原因分析总结 前言 今天遇到了一个有意思的问题,线上数据库 CPU 出现了偶发的抖动。定位到原因是一条查询语句偶发变慢造成的,随后通过调整表中的索引解决。 问题描述 下方是脱敏后的 SQL 语句: select oss_path f…...

SpringBoot自动连接数据库的解决方案
在一次学习设计模式的时候,沿用一个旧的boot项目,想着简单,就把数据库给关掉了,结果报错 Consider the following: If you want an embedded database (H2, HSQL or Derby), please put it on the classpath. 没有数据库的需…...

Docker-10 Docker Compose
一、前言 通过前面几篇文章的学习,我们可以通过Dockerfile文件让用户很方便的定义一个单独的应用容器。然而,在日常工作中,经常会碰到需要多个容器相互配合来完成某项任务的情况,或者开发一个Web应用,除了Web服务容器本身,还需要数据库服务容器、缓存容器,甚至还包括负…...

new mars3d.control.MapSplit({实现点击卷帘两侧添加不同图层弹出不同的popup
new mars3d.control.MapSplit({实现点击卷帘两侧添加不同图层弹出不同的popup效果: 左侧: 右侧: 说明:mars3d的3.7.12以上版本才支持该效果。 示例链接: 功能示例(Vue版) | Mars3D三维可视化平台 | 火星科技 相关代…...

数据库中虚拟表和临时表的区别?
虚拟表(Virtual Table)和临时表(Temporary Table)在数据库系统中都用于处理暂时性的数据存储需求,但它们的概念和用途有所不同: 虚拟表(通常是视图View): 虚拟表&#…...

Node.js -- mongoose
文章目录 1. 介绍2. mongoose 连接数据库3. 插入文件4. 字段类型5. 字段值验证6. 文档处理6.1 删除文档6.2 更新文档6.3 读取文档 7. 条件控制8. 个性化读取9. 代码模块化 1. 介绍 Mongoose是一个对象文档模型库,官网http://www.mongoosejs.net/ 方便使用代码操作mo…...
保持亮灯:监控工具如何确保 DevOps 中的高可用性
在快速发展的 DevOps 领域,保持高可用性 (HA) 至关重要。消费者期望应用程序具有全天候响应能力和可访问性。销售损失、客户愤怒和声誉受损都是停机的后果。为了使 DevOps 团队能够在问题升级为中断之前主动检测、排除故障并解决问题,监控工具成为这种情…...
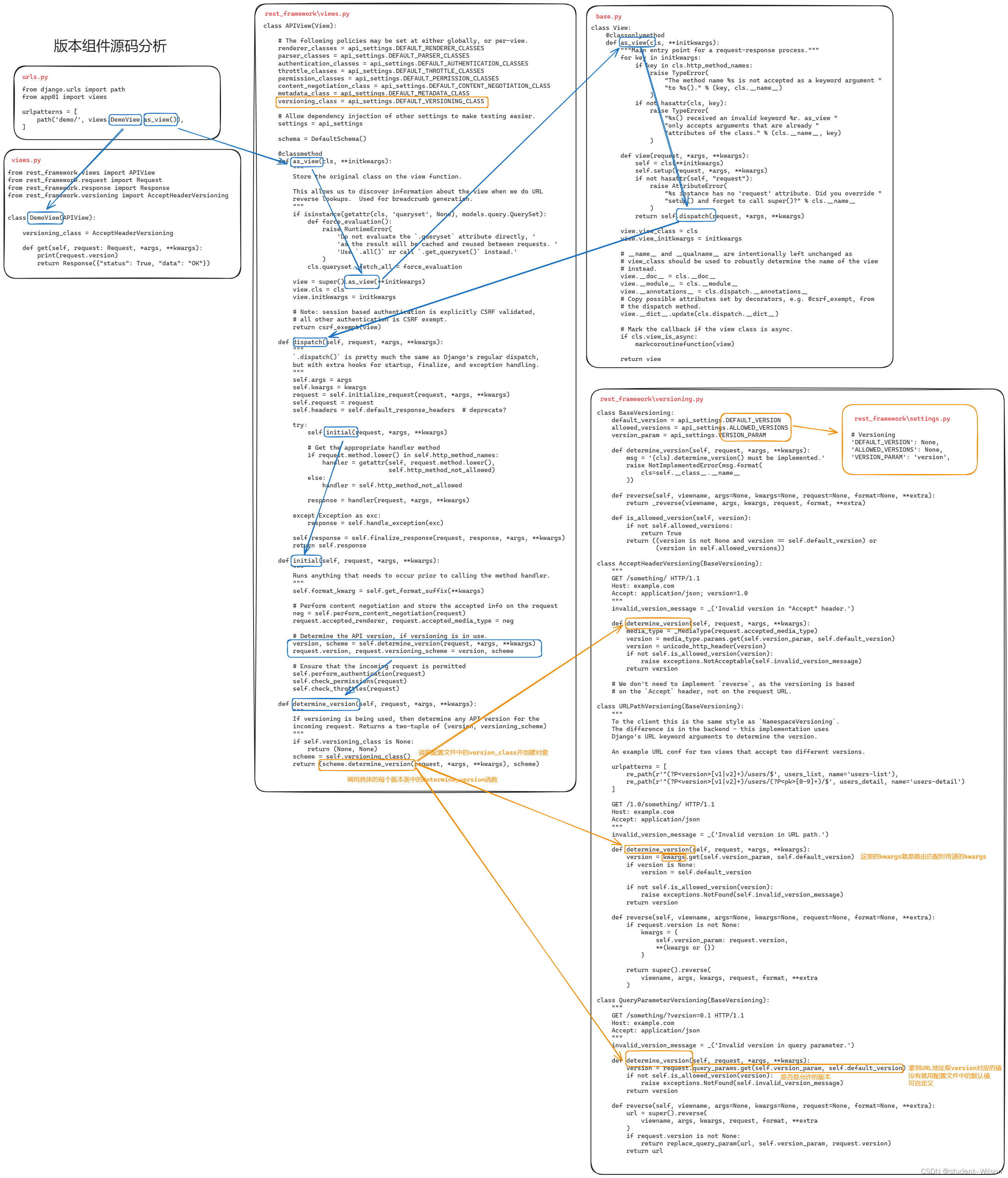
DRF版本组件源码分析
DRF版本组件源码分析 在restful规范中要去,后端的API中需要体现版本。 3.6.1 GET参数传递版本 from rest_framework.versioning import QueryParameterVersioning单视图应用 多视图应用 # settings.pyREST_FRAMEWORK {"VERSION_PARAM": "versi…...

C#算法之希尔排序
算法释义:希尔排序,也被称为缩小增量排序,是一种有效的排序算法,它是插入排序的一种更高效的改进版,通过比较一定间隔的元素来工作,然后逐步较少间隔来排序。 小编的理解啊,希尔排序的本质就是不…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...

【AI News | 20250609】每日AI进展
AI Repos 1、OpenHands-Versa OpenHands-Versa 是一个通用型 AI 智能体,通过结合代码编辑与执行、网络搜索、多模态网络浏览和文件访问等通用工具,在软件工程、网络导航和工作流自动化等多个领域展现出卓越性能。它在 SWE-Bench Multimodal、GAIA 和 Th…...
代理服务器-LVS的3种模式与调度算法
作者介绍:简历上没有一个精通的运维工程师。请点击上方的蓝色《运维小路》关注我,下面的思维导图也是预计更新的内容和当前进度(不定时更新)。 我们上一章介绍了Web服务器,其中以Nginx为主,本章我们来讲解几个代理软件:…...

Java毕业设计:办公自动化系统的设计与实现
JAVA办公自动化系统 一、系统概述 本办公自动化系统基于Java EE平台开发,实现了企业日常办公的数字化管理。系统包含文档管理、流程审批、会议管理、日程安排、通讯录等核心功能模块,采用B/S架构设计,支持多用户协同工作。系统使用Spring B…...
