练习题(2024/5/6)
1路径总和 II
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
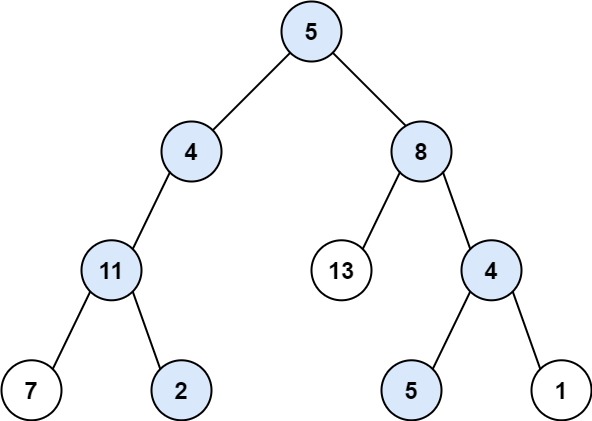
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
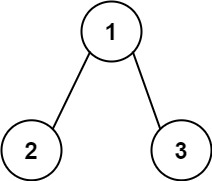
输入:root = [1,2,3], targetSum = 5 输出:[]
示例 3:
输入:root = [1,2], targetSum = 0 输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
思路:
.路径总和ii要遍历整个树,找到所有路径,所以递归函数不要返回值
-
定义数据结构:首先定义了一个
Solution类,其中包含了私有成员变量result和path,分别用于存放最终结果和当前路径。 -
递归遍历:通过递归方式遍历二叉树的每个节点,从根节点开始向下遍历。递归函数
traversal的参数包括当前节点指针cur和距离目标和还剩余的count。 -
叶子节点检查:在递归过程中,如果当前节点是叶子节点且剩余目标和
count为 0,说明找到了一条满足条件的路径,将该路径添加到结果中。 -
路径更新与回溯:在遍历过程中,将经过的节点值添加到
path数组中,同时更新剩余目标和count。然后递归遍历左右子树。在递归返回后,需要回溯,即将最后一个节点值移出path数组,以便尝试其他路径。 -
路径总和函数:
pathSum函数是对递归遍历的入口函数,首先清空之前的结果和路径,然后将根节点的值加入初始路径,并调用traversal函数开始递归遍历。
代码:
// 定义 Solution 类
class Solution {
private:vector<vector<int>> result; // 存放最终结果的二维数组vector<int> path; // 存放当前路径的节点值的一维数组// 递归遍历函数,参数为当前节点指针 cur 和距离目标和还剩余的 countvoid traversal(TreeNode* cur, int count) {// 如果当前节点是叶子节点且 count 等于 0,将当前路径添加到结果中if (cur->left == nullptr && cur->right == nullptr && count == 0) {result.push_back(path);return;}// 递归遍历左子树if (cur->left) {path.push_back(cur->left->val); // 将左子节点值加入路径count -= cur->left->val; // 更新剩余目标和traversal(cur->left, count); // 递归遍历左子树count += cur->left->val; // 恢复剩余目标和path.pop_back(); // 移除最后一个节点值,回溯}// 递归遍历右子树if (cur->right) {path.push_back(cur->right->val); // 将右子节点值加入路径count -= cur->right->val; // 更新剩余目标和traversal(cur->right, count); // 递归遍历右子树count += cur->right->val; // 恢复剩余目标和path.pop_back(); // 移除最后一个节点值,回溯}}public:// 求解路径总和的函数,参数为根节点指针 root 和目标和 targetSumvector<vector<int>> pathSum(TreeNode* root, int targetSum) {result.clear(); // 清空之前的结果path.clear(); // 清空之前的路径if (root == nullptr) return result; // 如果根节点为空,直接返回空结果path.push_back(root->val); // 将根节点的值加入初始路径traversal(root, targetSum - root->val); // 调用递归遍历函数return result; // 返回结果数组}
};2从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1] 输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
思路:
一层一层切割,就应该想到了递归。
一共分以下几步:
-
如果数组大小为零的话,说明是空节点了。
-
如果不为空,那么取后序数组最后一个元素作为节点元素。
-
如果当前节点是叶子节点(后序数组大小为1),直接创建该节点并返回。
-
找到当前节点在中序遍历数组中的位置,以此位置作为左右子树的分界点。
-
切割中序遍历数组,得到左子树和右子树的中序数组。
-
舍弃后序遍历数组末尾元素,因为这个元素作为当前节点。
-
根据左子树中序数组的大小,切割后序遍历数组,得到左子树和右子树的后序数组。
-
递归构建左子树和右子树。
-
将左子树和右子树连接到当前节点的左右孩子上。
代码的解题思路:
-
递归函数:
traversal函数是一个递归函数,用于构建二叉树。它接受两个参数:inorder是中序遍历数组,postorder是后序遍历数组。 -
基准情况: 如果后序遍历数组为空,说明当前子树为空,直接返回空指针。
-
根节点: 后序遍历数组的最后一个元素是当前子树的根节点。在每次递归调用中,我们取出后序遍历数组的最后一个元素作为当前子树的根节点,并创建一个
TreeNode对象。 -
叶子节点: 如果后序遍历数组的大小为 1,说明当前节点是叶子节点,直接返回当前节点。
-
中序遍历中的根节点位置: 我们在中序遍历数组中找到根节点的位置,以便将中序数组分割为左子树和右子树。
-
切割中序数组: 使用根节点在中序遍历数组中的位置来切割中序数组,以得到左子树和右子树的中序遍历数组。
-
舍弃后序遍历数组末尾元素: 后序遍历数组的最后一个元素是根节点,所以在递归调用左右子树构建后,我们需要舍弃后序遍历数组的末尾元素,以便构建左右子树。
-
切割后序数组: 使用左子树的中序数组的大小来切割后序数组,以得到左子树和右子树的后序遍历数组。
-
递归构建左右子树: 分别对左子树和右子树进行递归调用,构建左右子树,并将它们分别连接到当前节点的左右孩子。
-
主函数:
buildTree是主函数,用于检查输入数组的有效性,并调用traversal函数来构建整个二叉树。
代码:
class Solution {
private:// 定义递归函数,用于构建二叉树TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {// 如果后序遍历数组为空,返回空指针if (postorder.size() == 0) return NULL;// 后序遍历数组最后一个元素,即当前子树的根节点值int rootValue = postorder[postorder.size() - 1];TreeNode* root = new TreeNode(rootValue);// 如果当前节点是叶子节点,直接返回该节点if (postorder.size() == 1) return root;// 找到当前根节点在中序遍历数组中的位置int delimiterIndex;for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}// 切割中序数组,左闭右开区间:[0, delimiterIndex)vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);// [delimiterIndex + 1, end)vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );// 舍弃后序遍历数组末尾元素,因为该元素是当前树的根节点postorder.resize(postorder.size() - 1);// 切割后序数组// 依然左闭右开,使用左中序数组大小作为切割点// [0, leftInorder.size)vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());// [leftInorder.size(), end)vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());// 递归构建左右子树root->left = traversal(leftInorder, leftPostorder);root->right = traversal(rightInorder, rightPostorder);return root;}
public:// 主函数,用于构建二叉树TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {// 如果中序遍历数组或后序遍历数组为空,返回空指针if (inorder.size() == 0 || postorder.size() == 0) return NULL;// 调用递归函数return traversal(inorder, postorder);}
};3合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
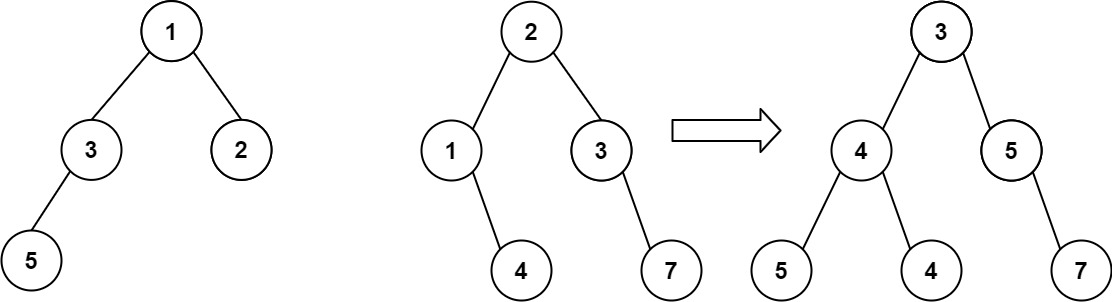
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2] 输出:[2,2]
提示:
- 两棵树中的节点数目在范围
[0, 2000]内 -104 <= Node.val <= 104
思路:
-
递归函数:
mergeTrees函数是一个递归函数,用于合并两棵二叉树。它接受两个参数root1和root2,分别表示两棵待合并的二叉树的根节点。 -
基准情况: 如果
root1为空,说明第一棵树为空,直接返回root2;如果root2为空,说明第二棵树为空,直接返回root1。 -
递归合并左子树和右子树: 对于当前节点,递归地合并它们的左子树和右子树,分别调用
mergeTrees函数,将合并后的左子树和右子树连接到当前节点的左孩子和右孩子上。 -
合并当前节点的值: 将两棵树当前节点的值相加,并更新到
root1节点上。 -
返回根节点: 返回合并后的第一棵树的根节点
root1。
代码:
class Solution {
public:// 合并两棵二叉树TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {// 如果第一棵树为空,返回第二棵树if (root1 == nullptr) return root2;// 如果第二棵树为空,返回第一棵树if (root2 == nullptr) return root1;// 递归合并左子树root1->left = mergeTrees(root1->left, root2->left);// 递归合并右子树root1->right = mergeTrees(root1->right, root2->right); // 修正此处的错误// 合并当前节点的值root1->val += root2->val;// 返回合并后的第一棵树的根节点return root1;}
};4按日期分组销售产品
SQL Schema
Pandas Schema
表 Activities:
+-------------+---------+ | 列名 | 类型 | +-------------+---------+ | sell_date | date | | product | varchar | +-------------+---------+ 该表没有主键(具有唯一值的列)。它可能包含重复项。 此表的每一行都包含产品名称和在市场上销售的日期。
编写解决方案找出每个日期、销售的不同产品的数量及其名称。
每个日期的销售产品名称应按词典序排列。
返回按 sell_date 排序的结果表。
结果表结果格式如下例所示。
示例 1:
输入:
Activities 表:
+------------+-------------+
| sell_date | product |
+------------+-------------+
| 2020-05-30 | Headphone |
| 2020-06-01 | Pencil |
| 2020-06-02 | Mask |
| 2020-05-30 | Basketball |
| 2020-06-01 | Bible |
| 2020-06-02 | Mask |
| 2020-05-30 | T-Shirt |
+------------+-------------+
输出:
+------------+----------+------------------------------+
| sell_date | num_sold | products |
+------------+----------+------------------------------+
| 2020-05-30 | 3 | Basketball,Headphone,T-shirt |
| 2020-06-01 | 2 | Bible,Pencil |
| 2020-06-02 | 1 | Mask |
+------------+----------+------------------------------+
解释:
对于2020-05-30,出售的物品是 (Headphone, Basketball, T-shirt),按词典序排列,并用逗号 ',' 分隔。
对于2020-06-01,出售的物品是 (Pencil, Bible),按词典序排列,并用逗号分隔。
对于2020-06-02,出售的物品是 (Mask),只需返回该物品名。思路:
- 从
Activities表中查询销售日期(sell_date)和产品(product)信息。 - 使用 count
(distinct product)函数计算每个销售日期下售出的产品的数量,并将结果命名为num_sold。 - 使用 group
_concat(distinct product order by product asc separator ',')函数将每个销售日期下售出的产品按照产品名字升序排列,并以逗号分隔合并成一个字段,命名为products。 - 使用 group
by sell_date将结果按照销售日期分组。 - 使用 order
by sell_date将结果按照销售日期进行升序排序。
group_concat 是一种用于将查询结果集中的多行合并成单行的函数,通常用于将多行数据合并成一行展示。它可以用在 SELECT 查询中,在 GROUP BY 子句的聚合函数中使用。
下面是一个示例用法:
SELECT department_id,GROUP_CONCAT(employee_name ORDER BY hire_date SEPARATOR ', ') AS employees
FROM employees
GROUP BY department_id; 在上面的例子中,假设 employees 表包含了部门ID和雇员名字等信息,通过使用 group_concat 函数按照部门ID分组,将每个部门的雇员名字合并成一行,并按照入职日期排序以逗号分隔显示
代码:
select sell_date,count(distinct product) as num_sold,
group_concat(distinct product order by product asc separator ',')
as products
from Activities
group by sell_date
order by sell_date相关文章:

练习题(2024/5/6)
1路径总和 II 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:root [5,4,8,11,null,13,4,7,2,null,null,5,1], target…...
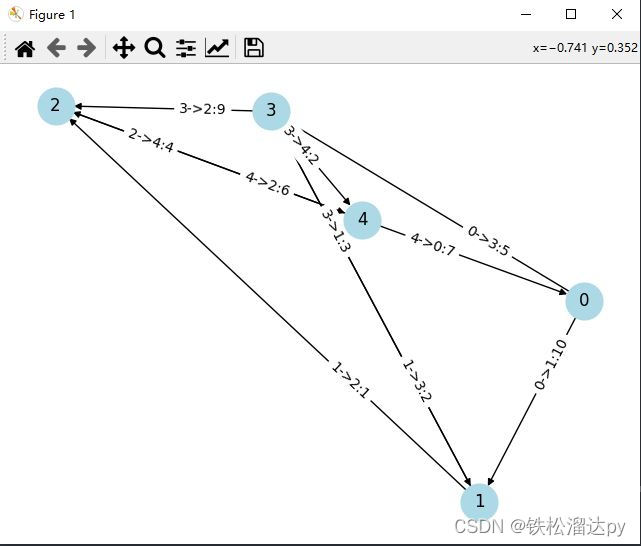
利用matplotlib和networkx绘制有向图[显示边的权重]
使用Python中的matplotlib和networkx库来绘制一个有向图,并显示边的权重标签。 1. 定义了节点和边:节点是一个包含5个节点的列表,边是一个包含各个边以及它们的权重的列表。 2. 创建了一个有向图对象 G。 3. 向图中添加节点和边。 4. 设置了…...
Springboot+Vue项目-基于Java+MySQL的教学资料管理系统(附源码+演示视频+LW)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:Java毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计 &…...

从NoSQL到NewSQL——10年代大数据浪潮下的技术革新
引言 在数字化浪潮的推动下,数据库技术已成为支撑数字经济的坚实基石。腾讯云 TVP《技术指针》联合《明说三人行》特别策划的直播系列——【中国数据库前世今生】,我们将通过五期直播,带您穿越五个十年,深入探讨每个时代的数据库演…...

巴菲特股东大会5万字完整版来了!
北京时间5月4日晚22:15,一年一度的伯克希尔股东大会在美国小镇奥马哈重磅开幕。 在今年的伯克希尔股东大会上,比尔盖茨、苹果CEO蒂姆库克等商界大佬均现身大会现场。 在股东大会上,巴菲特先后谈到了已故老搭档芒格、减持苹果、AI影响、现金储…...

LY/T 1860-2022 非甲醛类热塑性树脂胶合板检测
热塑性树脂胶合板是指以木质单板为原料,以聚乙烯、聚丙烯等非甲醛类热塑性树脂为胶黏剂制备的一种普通胶合板。 LY/T 1860-2022非甲醛类热塑性树脂胶合板测试项目: 测试项目 测试方法 外观 GB/T 9846 尺寸 GB/T 9846 含水率 GB/T 17657 胶合强度…...

信息管理与信息系统就业方向及前景分析
信息管理与信息系统(IMIS)专业的就业方向十分广泛,包含计算机方向、企业信息化管理、数据处理和数据分析等,随着大数据、云计算、人工智能、物联网等技术的兴起,对能够处理复杂信息系统的专业人才需求激增,信息管理与信息系统就业…...

TCP的三次握手过程
TCP是面向连接的、可靠的、基于字节流的传输层通信协议。 TCP是面向连接的协议,所以使用 TCP前必须先建立连接,而建立连接是通过三次握手来进行的。 TCP包头结构 在讲解三次握手的过程之前,我们先来看一下 TCP包的结构: TCP包…...

Microsoft 推出 Phi-3 系列紧凑型语言模型
本心、输入输出、结果 文章目录 Microsoft 推出 Phi-3 系列紧凑型语言模型前言Phi-3 基础参数模型对比突破性训练技术降低人工智能安全风险Microsoft 推出 Phi-3 系列紧凑型语言模型 编辑 | 简简单单 Online zuozuo 地址 | https://blog.csdn.net/qq_15071263 如果觉得本文对你…...

Retrofit库中,Call;Retrofit使用举例;@GET,@PUT区别;
目录 在Retrofit库中,Call Retrofit使用举例 Call> listRepos(@Path("user") String user); Call是什么:...
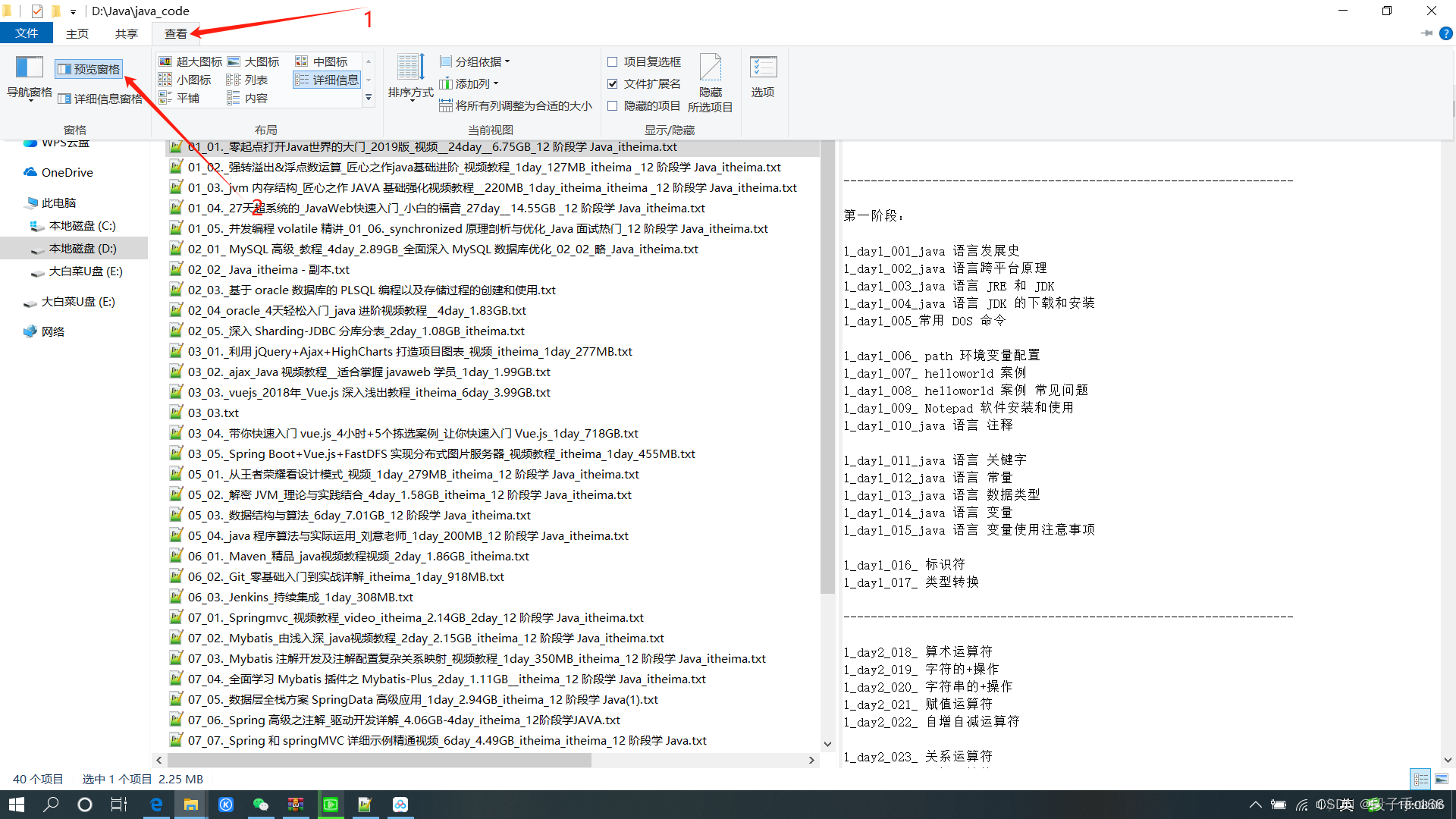
# 怎么关闭 win10 系统中自带的【文件预览】功能?关闭WIN10【文件预览】功能的方法
怎么关闭 win10 系统中自带的【文件预览】功能?关闭WIN10【文件预览】功能的方法 win10 系统中自带的【文件预览】功能,默认是开启状态的,如果需要关闭它,一步搞定。 1、打开电脑文件浏览器,随便进入有文件的一个文件…...

强化学习玩flappy_bird
强化学习玩flappy_bird(代码解析) 游戏地址:https://flappybird.io/ 该游戏的规则是: 点击屏幕则小鸟立即获得向上速度。 不点击屏幕则小鸟受重力加速度影响逐渐掉落。 小鸟碰到地面会死亡,碰到水管会死亡。&#…...
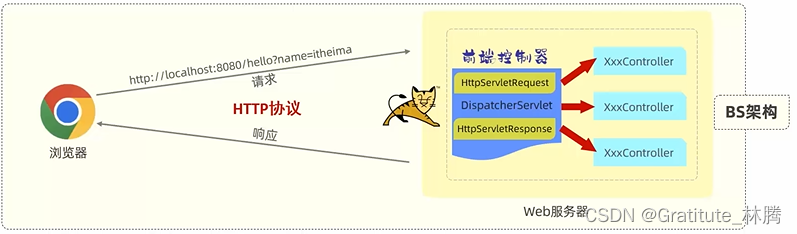
JavaWeb请求响应概述
目录 一、请求响应流程-简述 二、深入探究 三、DispatcherServlet 四、请求响应流程-详细分析 一、请求响应流程-简述 web应用部署在tomcat服务器中,前端与后端通过http协议进行数据的请求和响应。前端通过http协议向后端发送数据请求,就可以访问到部…...

【IDEA】IDEA常用快捷键
Windows系统 快捷键功能备注CtrlShiftEnter格式化本行,并鼠标跳转到下一行CtrlAltL格式化代码Ctrli快速实现接口方法CtrlShiftU快速实现大小写转换CtrlAlt鼠标左键快速进入方法实现内部CtrlAlt←退回上一步鼠标所在地方CtrlAlt→回到刚才鼠标所在地方Ctrl空格代码智…...

Redission分布式锁 watch dog 看门狗机制
为了避免Redis实现的分布式锁超时,Redisson中引入了watch dog的机制,他可以帮助我们在Redisson实例被关闭前,不断的延长锁的有效期。 自动续租:当一个Redisson客户端实例获取到一个分布式锁时,如果没有指定锁的超时时…...
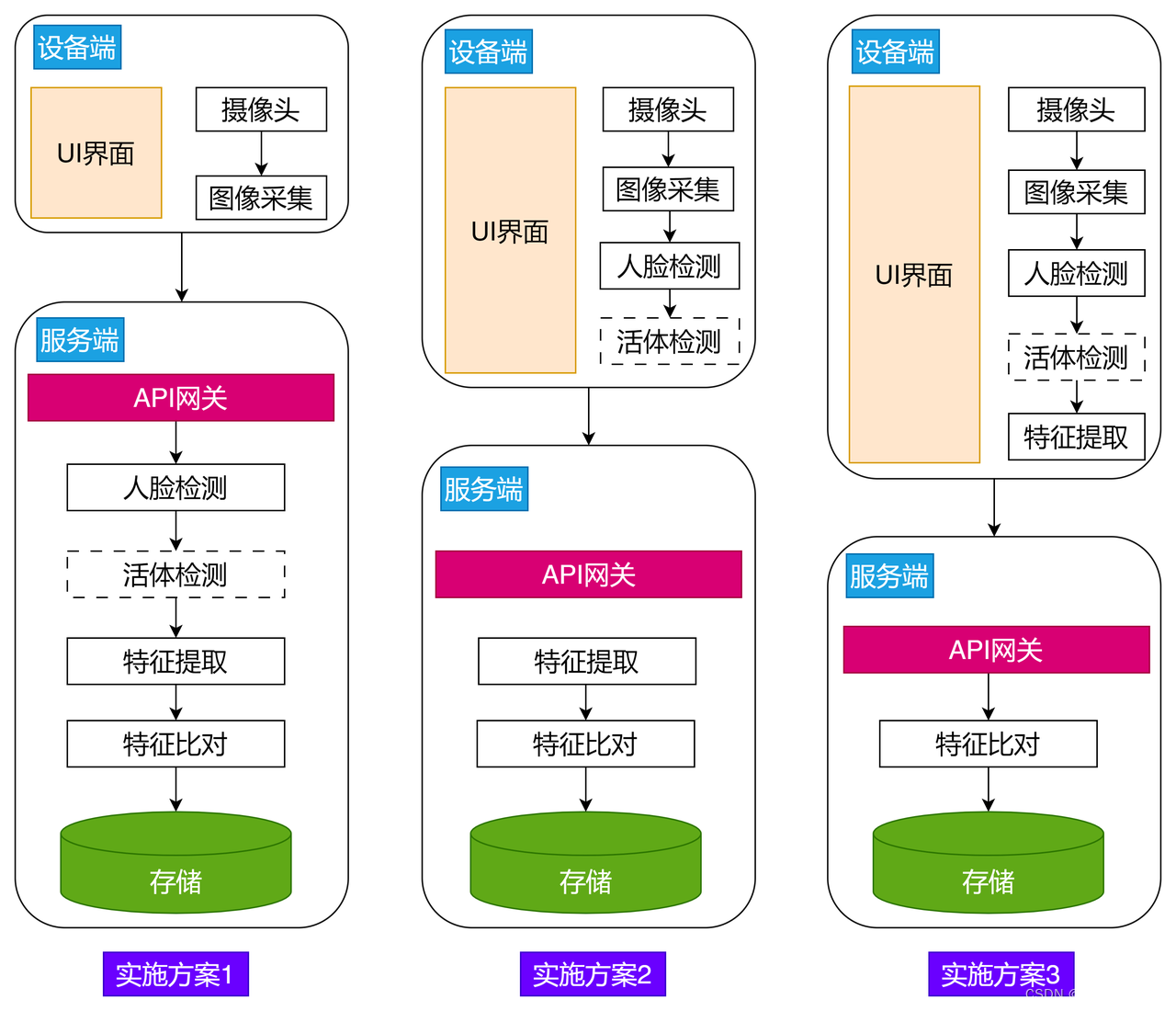
人脸识别系统架构
目录 1. 系统架构 1.1 采集子系统 1.2 解析子系统 1.3 存储子系统 1.4 比对子系统 1.5 决策子系统 1.6 管理子系统 1.7 应用开放接口 2. 业务流程 2.1 人脸注册 2.2 人脸验证 2.2.1 作用 2.2.2 特点 2.2.3 应用场景 2.3 人脸辨识 2.3.1 作用 2.3.2 特点 2.3.3…...
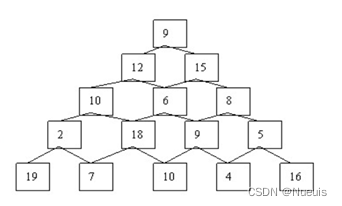
数塔问题(蛮力算法和动态规划)
题目:如下图是一个数塔,从顶部出发在每一个节点可以选择向左或者向右走,一直走到底层,要求找出一条路径,使得路径上的数字之和最大,及路径情况。(使用蛮力算法和动态规划算法分别实现) #include…...

启动 Redis 服务和连接到 Redis 服务器
启动 Redis 服务和连接到 Redis 服务器的步骤通常依赖于你的操作系统和 Redis 的安装方式。以下是一些常见的步骤: ### 启动 Redis 服务 对于大多数 Linux 发行版,Redis 服务可以通过以下命令启动: 1. 如果 Redis 是通过包管理器安装的&am…...
我独自升级崛起在哪下载 我独自升级电脑PC端下载教程分享
将于5月8日在全球舞台闪亮登场的动作角色扮演游戏《我独自升级崛起》,灵感源自同名热门动画与网络漫画,承诺为充满激情的游戏玩家群体带来一场集深度探索与广阔体验于一身的奇幻旅程。该游戏以独特的网络武侠世界观为基底,展现了一位普通人踏…...

STM32F4xx开发学习—GPIO
GPIO 学习使用STM32F407VET6GPIO外设 寄存器和标准外设库 1. 寄存器 存储器映射 存储器本身是不具有地址的,是一块具有特定功能的内存单元,它的地址是由芯片厂商或用户分配,给存储器分配地址的过程就叫做存储区映射。给内存单元分配地址之后…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

C#中用于控制自定义特性(Attribute)
我们来详细解释一下 [AttributeUsage(AttributeTargets.Class, AllowMultiple false, Inherited false)] 这个 C# 属性。 在 C# 中,Attribute(特性)是一种用于向程序元素(如类、方法、属性等)添加元数据的机制。Attr…...

Git 使用大全:从入门到精通
Git 是目前最流行的分布式版本控制系统,被广泛应用于软件开发中。本文将全面介绍 Git 的各种功能和使用方法,包含大量代码示例和实践建议。 文章目录 Git 基础概念版本控制系统Git 的特点Git 的三个区域Git 文件状态 Git 安装与配置安装 GitLinuxmacOSWi…...
