刷题记录:牛客NC24048[USACO 2017 Jan P]Promotion Counting 求子树的逆序对个数
传送门:牛客
题目描述
奶牛们又一次试图创建一家创业公司,还是没有从过去的经验中吸取教训–牛是可怕的管理者!
为了方便,把奶牛从 1∼n1\sim n1∼n 编号,把公司组织成一棵树,1 号奶牛作为总裁(这棵树的根节点)。除了总裁以外的每头奶牛都有一个单独的上司(它在树上的 “双亲结点”)。
所有的第 iii 头牛都有一个不同的能力指数 pip_ipi,描述了她对其工作的擅长程度。如果奶牛 iii 是奶牛 jjj 的祖先节点,那么我们我们把奶牛 jjj 叫做 iii 的下属。
不幸地是,奶牛们发现经常发生一个上司比她的一些下属能力低的情况,在这种情况下,上司应当考虑晋升她的一些下属。你的任务是帮助奶牛弄清楚这是什么时候发生的。简而言之,对于公司的中的每一头奶牛 iii,请计算其下属 jjj 的数量满足 pj>pip_j > p_ipj>pi。
输入:
5
804289384
846930887
681692778
714636916
957747794
1
1
2
3
输出:
2
0
1
0
0
刚开始我以为是一道树链剖分的题目.然后发现这道题本质上应该是一道树上dfsdfsdfs的题目
当然树链剖分暴力解决这道题也是可以做的,对于树剖,复杂度时log级别的.可以考虑使用树剖将树形结构转化为线性结构,然后考虑维护区间逆序对个数.此时我们无法使用线段树进行维护.对于维护区间逆序对个数,我们考虑使用分块进行维护,朴素莫队可以在NNlogNN\sqrt{N}logNNNlogN解决.复杂度还是满足本题的.但是使用上述方法解决本题是在是杀鸡用牛刀,本题还是用不到那么复杂的维护方法的
对于本题来说,我们只需要计算一个节点的所有儿子的贡献即.因为父亲对儿子是没有贡献的,所以我们考虑使用dfsdfsdfs来解决这道题.使用权值树状数组(当然权值线段树也是可以的)来维护每一个权值.那么对于一个节点uuu来说,我们只需要遍历他的所有儿子节点,并且将所有权值都存入权值树状数组中,然后对于uuu节点的答案来说,就是当前比他大的节点的个数.但是这么做的话存在一个问题,因为我们的这棵BIT此时存的不只是当前结点的儿子的权值,之前遍历其他节点的时候也存了,所以此时会导致一些错误.解决此问题的方案是,在遍历该节点的儿子节点之前先减去之前所有已在节点的贡献即可.这样的话就相当于减去了其他不满足子树的贡献
本题需要进行离散化操作
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int tree[maxn];int n;
int lowbit(int x) {return x&(~x+1);
}
void Add(int pos,int val) {while(pos<=n) {tree[pos]+=val;pos+=lowbit(pos);}
}
int query(int pos) {int ans=0;while(pos) {ans+=tree[pos];pos-=lowbit(pos);}return ans;
}
int w[maxn];vector<int>v;int Size;
vector<int>edge[maxn];int ans[maxn];
int get_id(int x) {return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void dfs1(int u,int per_u) {int x=get_id(w[u]);ans[u]-=query(Size)-query(x);for(int i=0;i<edge[u].size();i++) {int v=edge[u][i];if(v==per_u) continue;dfs1(v,u);}ans[u]+=query(Size)-query(x);Add(x,1);
}
int main() {n=read();for(int i=1;i<=n;i++) {w[i]=read();v.push_back(w[i]);}sort(v.begin(),v.end());Size=v.size();for(int i=2;i<=n;i++) {int u=read();edge[u].push_back(i);}dfs1(1,0);for(int i=1;i<=n;i++) printf("%d\n",ans[i]);return 0;
}
相关文章:

刷题记录:牛客NC24048[USACO 2017 Jan P]Promotion Counting 求子树的逆序对个数
传送门:牛客 题目描述 奶牛们又一次试图创建一家创业公司,还是没有从过去的经验中吸取教训–牛是可怕的管理者! 为了方便,把奶牛从 1∼n1\sim n1∼n 编号,把公司组织成一棵树,1 号奶牛作为总裁(这棵树的根…...

MpAndroidChart3最强实践攻略
本篇主要总结下Android非常火爆的一个三方库MpAndroidChart的使用。可能在大多数情况下,我们很少会在Android端去开发图表。但如果说去做一些金融财经类、工厂类、大数据类等的app,那么绝对会用到MpAndroidChart。 一、前言 2018年,那年的我…...
:事务管理ACID)
Spring笔记(9):事务管理ACID
一、事务管理 一个数据库事务是一个被视为单一的工作单元操作序列。 事务管理有四个原则,被成为ACID: Atomicity 原子性—— 事务作为独立单元进行操作,整个序列是一体的,操作全都成功或失败。Consistency 一致性—— 引用完整…...

io流 知识点+代码实例
需求 : 如何实现读写文件内部的内容?流 : 数据以先入先出的方式进行流动相当于管道,作用用来传输数据数据源-->流-->目的地流的分类 :流向分 : 以程序为中心输入流输出流操作单元 :字节流 : 万能流字符流 : 只能操作纯文本文件功能分 :节点流 : 真实实现读写的功能流(包…...
【MySQL】P8 多表查询(2) - 连接查询 联合查询
连接查询以及联合查询多表查询概述连接查询内连接隐式内连接显式内连接外连接左外连接右外连接自连接联合查询多表查询概述 建表语句见上一篇博文:https://blog.csdn.net/weixin_43098506/article/details/129402302 e.g.e.g.e.g. select * from emp, dept where e…...
QML动画(Animator)
在Qt5.2之后,引入Animator动画元素。这种方式可以直接所用于Qt Quick的场景图形系统,这使得基于Animator元素的动画及时在ui界面线程阻塞的情况下仍然能通过图形系统的渲染线程来工作,比传统的基于对象和属性的Animation元素能带来更好的用户…...
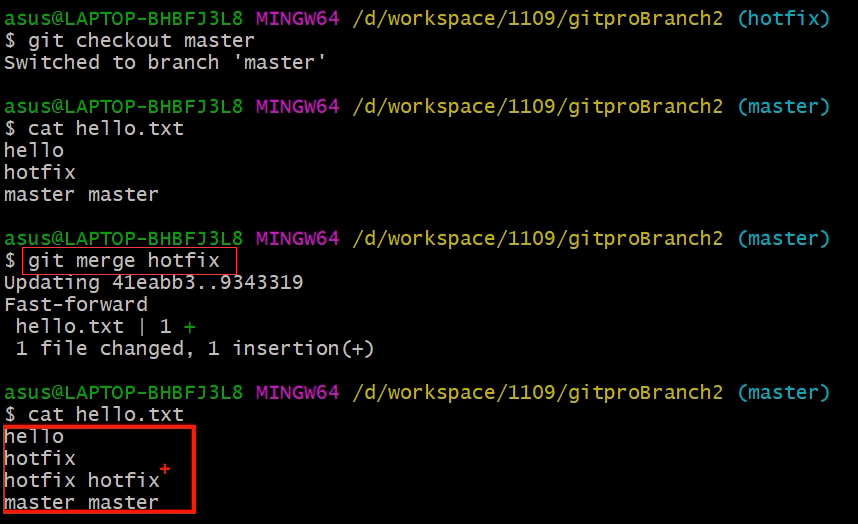
Git 分支操作【解决分支冲突问题】
1. 什么是分支 在版本控制过程中,同时推进多个任务,为每个任务,我们就可以创建每个任务的单独分支。使用分支意味着程序员可以把自己的工作从开发主线上分离开来,开发自己分支的时候,不会影响主线分支的运行。对于初学…...

盘点全球10大女性技术先驱
盘点全球10大女性技术先驱 人们普遍认为技术是男性主导的领域,但事实,技术或编程与性别无关,几乎任何人都可以成为技术大神。已经有很多案例证明女性同样可以在技术领域施展才能。在女神节来临之际,我为大家盘点一下为编程做出卓越…...

C++之dynamic_cast
C之dynamic_cast前言dynamic_castNote:示例:前言 dynamic_cast运算符牵扯到的面向对象的多态性跟程序运行时的状态,所以不能完全的使用传统的转换方式来替代。因此是最常用,最不可缺少的一个运算符,与static_cast一样,dynamic_cas…...

JavaScript 箭头函数、函数参数
箭头函数: 箭头函数是一种更加简洁的函数书写方式箭头函数本身没有作用域(无this)箭头函数的this指向上一层,上下文决定其this基本语法:参数 > 函数体 a. 基本用法 let fn v > v; //等价于 let fn function(…...

JavaScript_Object.keys() Object.values()
目录 一、Object.keys() 二、Object.values() 一、Object.keys() Object.keys( ) 的 用法 : 作用 :遍历对象 { } 返回结果:返回 对象中 每一项 的 key 值 返回值 : 是一个 *** [ 数 组 ] *** 例子 ( 1 ) : <script>// 1. 定义一个对象var obj …...

扬帆优配|高送转+高分红+高增长潜力股揭秘
高送转且高分红的高增加股票,有望跑赢大盘。 此前七连阴的泽宇智能,今日早盘大幅高开。到上午收盘,该股飙涨9.3%,位居涨幅榜前列。音讯面上,3月7日晚间,泽宇智能发表2022年年报,年报显现&#x…...
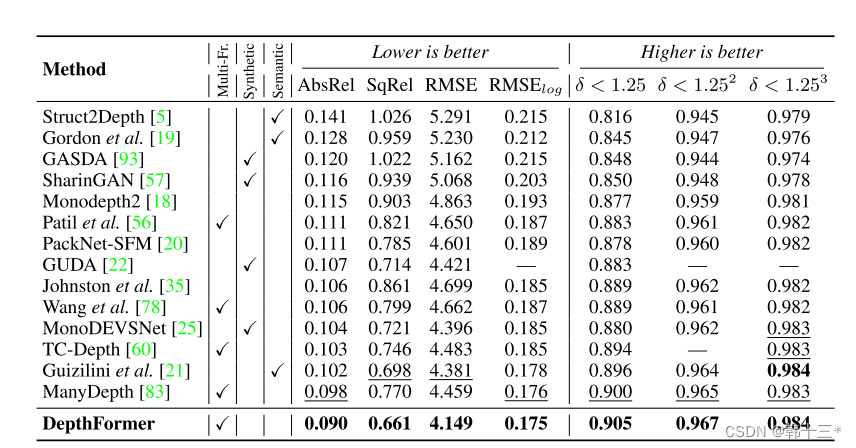
基于transformer的多帧自监督深度估计 Multi-Frame Self-Supervised Depth with Transformers
Multi-Frame Self-Supervised Depth with Transformers基于transformer的多帧自监督深度估计0 Abstract 多帧深度估计除了学习基于外观的特征外,也通过特征匹配利用图像之间的几何关系来改善单帧估计。我们采用深度离散的核极抽样来选择匹配像素,并通过一…...

设计模式: 单例模式
目录单例模式应用场景实现步骤涉及知识点设计与实现单例模式 通过单例模式的方法创建的类在当前进程中只有一个实例; 应用场景 配置管理 日志记录 线程池 连接池 内存池 对象池 消息队列 实现步骤 将类的构造方法定义为私有方法 定义一个私有的静态实例 提供一…...

idea编辑XML文件出现:Tag name expected报错
说明 Tag name expected解释其实就是:需要标记名称,也就是符号不能直接使用的意思 XML (eXtensible Markup Language) 是一种标记语言,用于存储和传输数据。在 XML 中,有些字符被视为特殊字符,这些字符在 XML 中具有…...

第十三届蓝桥杯省赛C++ A组 爬树的甲壳虫(简单概率DP)
题目如下: 思路 or 题解: 概率DP 状态定义: dp[i]dp[i]dp[i] 表示从树根到第 iii 层的期望 状态转移: dp[i](dp[i−1]1)∗11−pdp[i] (dp[i - 1] 1) * \frac{1}{1-p}dp[i](dp[i−1]1)∗1−p1 这个式子的意思是:…...
手动集成Tencent SDK遇到的坑!!!
手动集成的原因 由于腾讯未把Tencent SDK上传到Github中,所以我们不能通过Cocoapods的方式集成,只能通过官方下载其SDK手动集成。 Tencent SDK手动集成步骤 1.访问腾讯开放平台SDK下载界面,找到并下载iOS_SDK_V3.5.1。(目前最新…...
三天吃透mybatis面试八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...
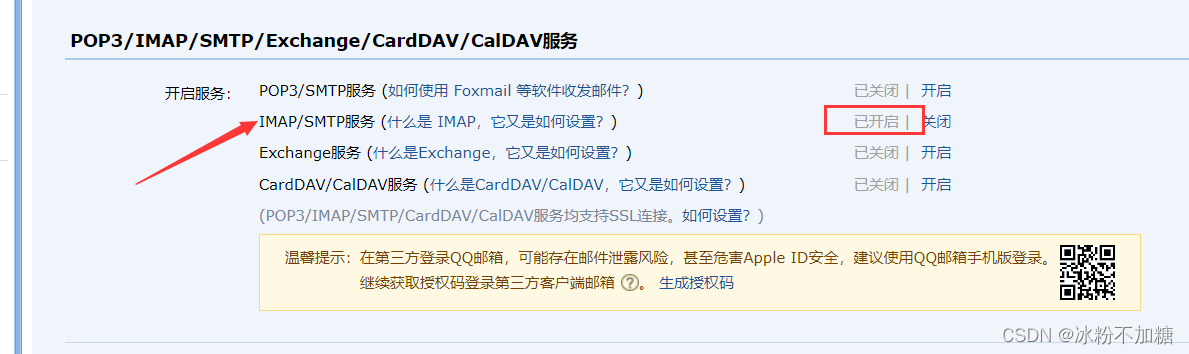
SpringBoot整合Quartz以及异步调用
文章目录前言一、异步方法调用1、导入依赖2、创建异步执行任务线程池3、创建业务层接口和实现类4、创建业务层接口和实现类二、测试定时任务1.导入依赖2.编写测试类,开启扫描定时任务3.测试三、实现定时发送邮件案例1.邮箱开启IMAP服务2.导入依赖3.导入EmailUtil4.编…...
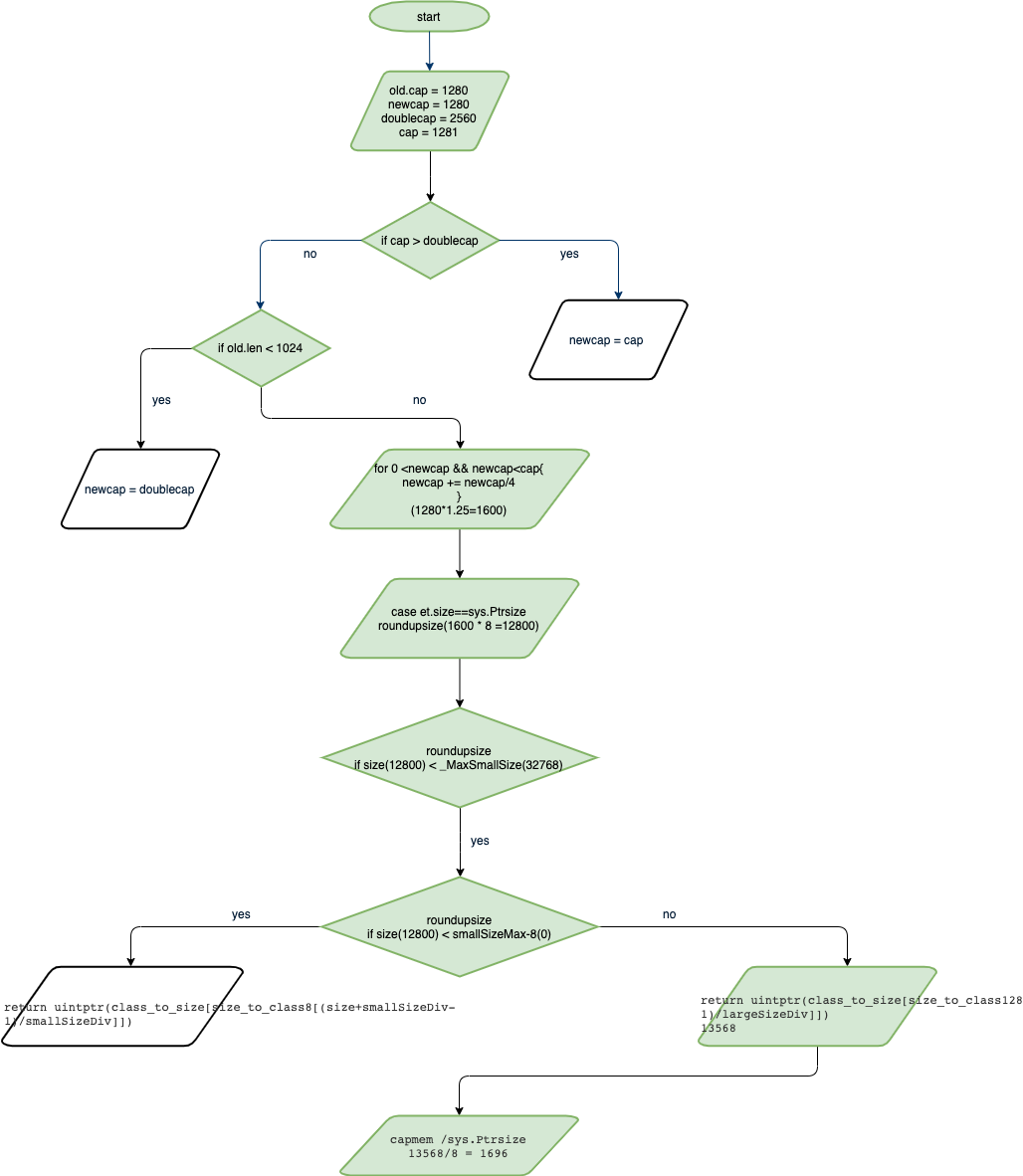
Golang 中 Slice的分析与使用(含源码)
文章目录1、slice结构体2、slice初始化3、append操作4、slice截取5、slice深拷贝6、值传递还是引用传递参考文献众所周知,在golang中,slice(切片)是我们最常使用到的一种数据结构,是一种可变长度的数组,本篇…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
