第十三届蓝桥杯省赛C++ A组 爬树的甲壳虫(简单概率DP)
题目如下:

思路 or 题解:
概率DP
状态定义:
dp[i]dp[i]dp[i] 表示从树根到第 iii 层的期望
状态转移:
dp[i]=(dp[i−1]+1)∗11−pdp[i] = (dp[i - 1] + 1) * \frac{1}{1-p}dp[i]=(dp[i−1]+1)∗1−p1
这个式子的意思是:从第 000 层出发,到第 iii 层的期望时间 E(i)E(i)E(i) 可以通过从第 000 层到第 i−1i-1i−1 层的期望时间 E(i−1)E(i-1)E(i−1) 加上一次上升所需要的期望时间(即 111)再乘以 11−p\frac{1}{1-p}1−p1。
在期望中,1/(1−p)1/(1-p)1/(1−p) 表示一个事件在不停地进行下去,直到该事件发生为止所需的期望次数。
简单解释一下这个 11−p\frac{1}{1-p}1−p1
以第一个样例为例子:
期望 = 1∗12+2∗14+3∗18....1 * \frac{1}{2} + 2 * \frac{1}{4} + 3 * \frac{1}{8} ....1∗21+2∗41+3∗81....
收敛与 11−p\frac{1}{1-p}1−p1
这个式子是 等差 ×\times× 等比
具体如何得到,再此不再多赘述。
答案计算
DP递推
AC 代码如下:
/*
Make it simple and keep self stupid
author:Joanh_Lan
*/
#pragma GCC optimize(3)
#pragma GCC optimize("inline") // 如果比赛允许开编译器优化的话,可以默写这两段
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <numeric>
#include <cstring>
#include <cmath>
#include <map>
#include <unordered_map>
#include <bitset>
#include <set>
#include <random>
#include <ctime>
#include <queue>
#include <stack>
#include <climits>
#define buff \ios::sync_with_stdio(false); \cin.tie(0);
#define int long long
#define ll long long
#define PII pair<int, int>
#define px first
#define py second
typedef std::mt19937 Random_mt19937;
Random_mt19937 rnd(time(0));
using namespace std;
const int mod = 998244353;
const int inf = 2147483647;
const int N = 100009;
int Mod(int a,int mod){return (a%mod+mod)%mod;}
//int lowbit(int x){return x&-x;}//最低位1及其后面的0构成的数值
int qmi(int a, int k, int p){int res = 1 % p;while (k){if (k & 1) res = Mod(res * a , p);a = Mod(a * a , p);k >>= 1;}return res;}
int inv(int a,int mod){return qmi(a,mod-2,mod);}
//int lcm(int a,int b){return a*b/__gcd(a,b);}
int n;
void solve()
{cin >> n;int ans = 0;for (int i = 1; i <= n; i++){int a, b; cin >> a >> b;ans = ((ans + 1) * b) % mod * inv(b - a, mod) % mod;}cout << ans << '\n';
}
signed main()
{buff;int _ = 1;// cin >> _;while (_--)solve();
}
相关文章:

第十三届蓝桥杯省赛C++ A组 爬树的甲壳虫(简单概率DP)
题目如下: 思路 or 题解: 概率DP 状态定义: dp[i]dp[i]dp[i] 表示从树根到第 iii 层的期望 状态转移: dp[i](dp[i−1]1)∗11−pdp[i] (dp[i - 1] 1) * \frac{1}{1-p}dp[i](dp[i−1]1)∗1−p1 这个式子的意思是:…...
手动集成Tencent SDK遇到的坑!!!
手动集成的原因 由于腾讯未把Tencent SDK上传到Github中,所以我们不能通过Cocoapods的方式集成,只能通过官方下载其SDK手动集成。 Tencent SDK手动集成步骤 1.访问腾讯开放平台SDK下载界面,找到并下载iOS_SDK_V3.5.1。(目前最新…...
三天吃透mybatis面试八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...
SpringBoot整合Quartz以及异步调用
文章目录前言一、异步方法调用1、导入依赖2、创建异步执行任务线程池3、创建业务层接口和实现类4、创建业务层接口和实现类二、测试定时任务1.导入依赖2.编写测试类,开启扫描定时任务3.测试三、实现定时发送邮件案例1.邮箱开启IMAP服务2.导入依赖3.导入EmailUtil4.编…...
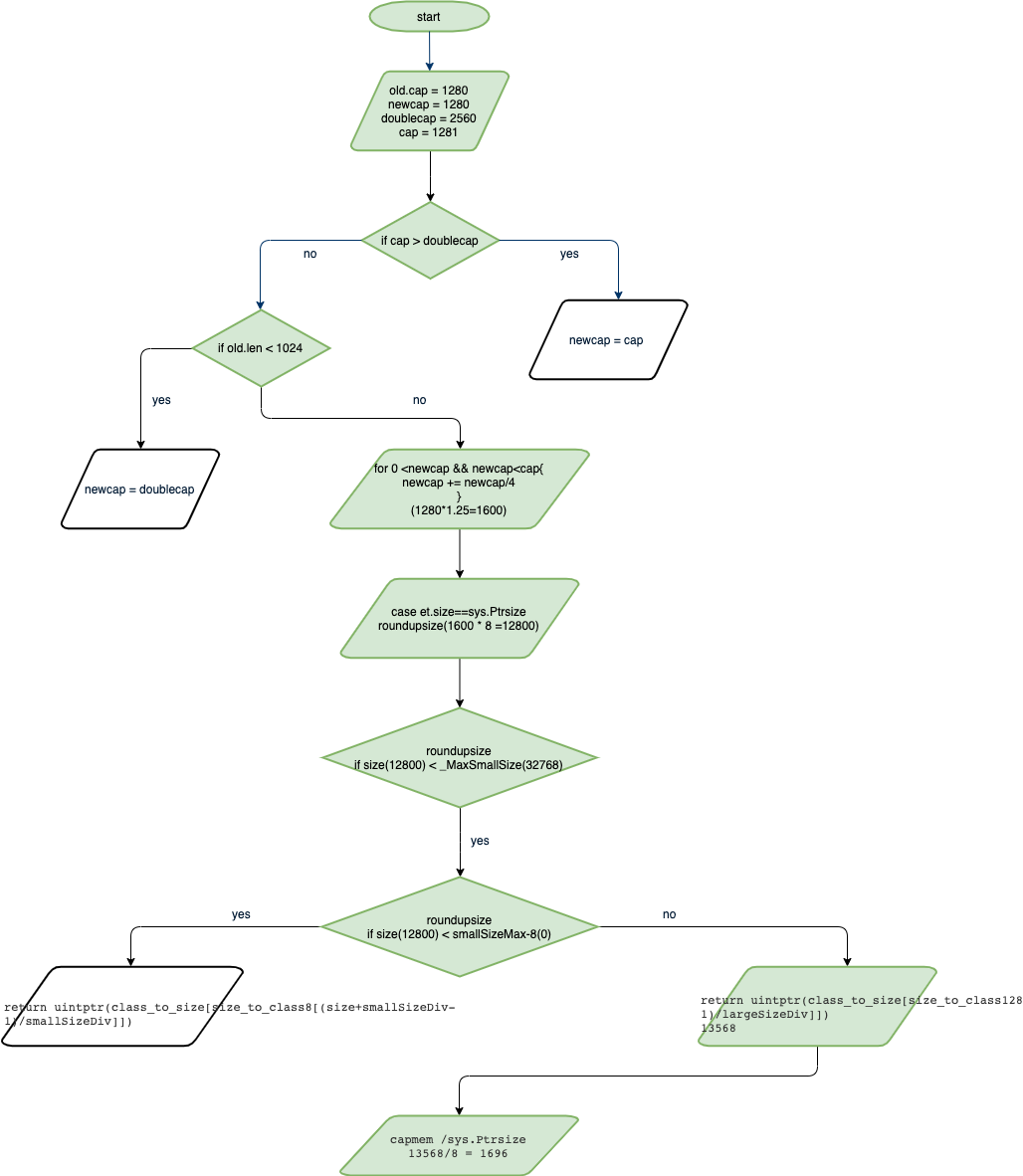
Golang 中 Slice的分析与使用(含源码)
文章目录1、slice结构体2、slice初始化3、append操作4、slice截取5、slice深拷贝6、值传递还是引用传递参考文献众所周知,在golang中,slice(切片)是我们最常使用到的一种数据结构,是一种可变长度的数组,本篇…...
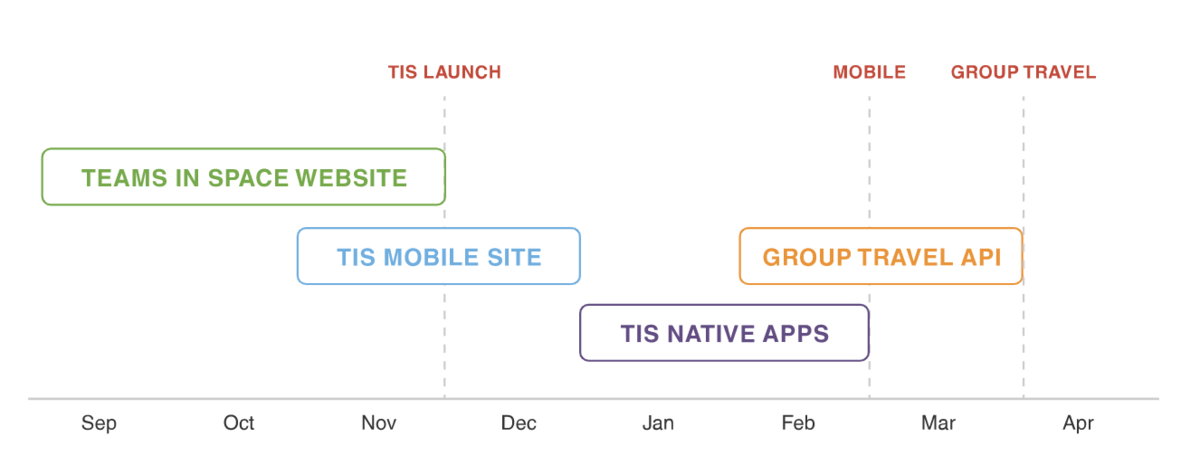
瀑布开发与敏捷开发的区别,以及从瀑布转型敏捷项目管理的5大注意事项
事实证明,瀑布开发管理模式并不适合所有的软件项目,但敏捷项目管理却对大多数项目有效。那么当团队选择转型敏捷的时候有哪些因素必须注意?敏捷开发最早使用者大多是小型、独立的团队,他们通常致力于小型、独立的项目。正是他们的…...
)
“华为杯”研究生数学建模竞赛2007年-【华为杯】A题:建立食品卫生安全保障体系数学模型及改进模型的若干理论问题(附获奖论文)
赛题描述 我国是一个拥有13亿人口的发展中国家,每天都在消费大量的各种食品,这批食品是由成千上万的食品加工厂、不可计数的小作坊、几亿农民生产出来的,并且经过较多的中间环节和长途运输后才为广大群众所消费,加之近年来我国经济发展迅速而环境治理没有能够完全跟上,以…...
基于JavaWeb学生选课系统开发与设计(附源码资料)
文章目录1. 适用人群2. 你将收获3.项目简介4.技术实现5.运行部分截图5.1.管理员模块5.2.教师模块5.3.学生模块1. 适用人群 本课程主要是针对计算机专业相关正在做毕业设计或者是需要实战项目的Java开发学习者。 2. 你将收获 提供:项目源码、项目文档、数据库脚本…...

centos7 oracle19c安装||新建用户|| ORA-01012: not logged on
总共分三步 1.下载安装包:里面有一份详细的安装教程 链接:https://pan.baidu.com/s/1Of2a72pNLZ-DDIWKrTQfLw?pwd8NAx 提取码:8NAx 2.安装后,执行初始化:时间较长 /etc/init.d/oracledb_ORCLCDB-19c configure 3.配置环境变量,不配置环境变量,sq…...
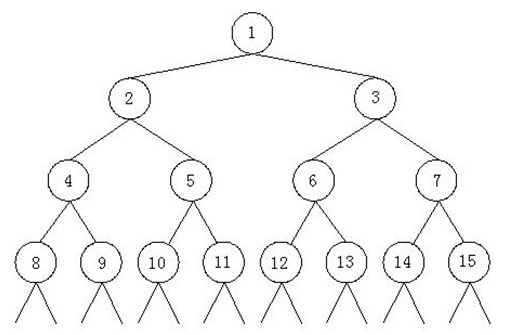
【算法设计-分治】递归与尾递归
文章目录1. 阶乘尾递归:递归的进一步优化2. 斐波那契数列3. 最大公约数(GCD)4. 上楼梯5. 汉诺塔(1)输出移动过程输出移动步数5. 汉诺塔(2)输出移动过程输出移动步数6. 杨辉三角形7. 完全二叉树1…...

HTML 编辑器
文章目录 HTML 编辑器HTML 编辑器推荐编辑器下载网站HBuilder步骤 1: 新建 HTML 文件步骤 2: 另存为 HTML 文件步骤 3: 在浏览器中运行这个 HTML 文件HTML 编辑器 HTML 编辑器推荐 可以使用专业的 HTML 编辑器来编辑 HTML,我为大家推荐几款常用的编辑器: Notepad++:Windows…...
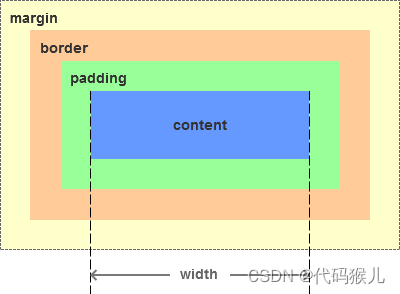
css盒模型详解
一、引言 盒模型是网页开发中的一个基本概念,它描述了网页元素的外观和大小。盒模型由内容区域、内边距、边框和外边距四个部分组成,这些部分的大小和位置都可以通过CSS进行控制。在本文中,我们将介绍盒模型的概念和作用,并提出本…...

函数模板(template关键字的应用)
注释:本文主要介绍了函数模板的由来以及用法,还有关键字template。 我们感到时间的延续像一条我们无法逆行的小溪。 ——柏格森 文章目录一、语言的定式二、函数模板2.1 函数模板格式2.2 模板函数的实例化2.2.1隐式实例化/显式实例化2.3 模板参数的匹配…...

嵌入式学习笔记——使用寄存器编程操作GPIO
使用寄存器编程操作GPIO前言GPIO相关的寄存器GPIO 端口模式寄存器 (GPIOx_MODER) (x A..I)位操作GPIO 端口输出类型寄存器 (GPIOx_OTYPER) (x A..I)GPIO 端口输出速度寄存器 (GPIOx_OSPEEDR) (x A..I/)GPIO 端口上拉/下拉寄存器 (GPIOx_PUPDR) (x A..I/)GPIO 端口输入数据寄…...

图像的读取与保存
图像是由一个个像素点组成,像素点就是颜色点,而颜色最简单的方式就是用RGB或RGBA表示图像保存图像将像素信息按照 一定格式,一定顺序(即编码) 存在硬盘上的 二进制文件 中保存图像需要以下必要信息:1. 文件…...

【蓝桥杯集训·每日一题】AcWing 4074. 铁路与公路
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴Floyd 算法Spfa 算法一、题目 1、原题链接 4074. 铁路与公路 2、题目描述 某国家有 n 个城市(编号 1∼n)和 m 条双向铁路。 每条铁路连接两个不同的…...
网络:TCP与UDP相关知识(详细)
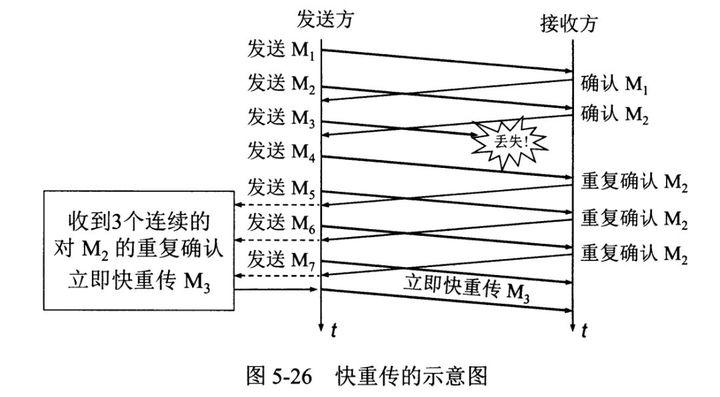
目录:1、UDP 和 TCP 的特点与区别2、UDP 、TCP 首部格式3、TCP 的三次握手和四次挥手4、TCP 的三次握手(为什么三次?)5、TCP 的四次挥手(为什么四次?)6、TCP 长连接和短连接的区别7、TCP粘包、拆…...
不好!有敌情,遭到XSS攻击【网络安全篇】
XSS:当一个目标的站点,被我们用户去访问,在渲染HTMl的过程中,出现了没有预期到的脚本指令,然后就会执行攻击者用各种方法注入并执行的恶意脚本,这个时候就会产生XSS。 涉及方: 用户࿰…...

Mysql中Explain详解及索引的最佳实践
Mysql中Explain详解及索引的最佳实践1.Explan工具的介绍1.1 Explan 分析示例1.2 Explain中的列1.2.1 id1.2.2 select_type1.2.3 table1.2.4 partitions1.2.5 type1.2.6 possible_keys1.2.7 key1.2.8 key_len1.2.9 ref1.2.10 rows1.2.11 filtered1.2.12 Extra1.Explan工具的介绍…...

JavaScript 内的 this 指向
在 javascript 语言中, 有一个奇奇怪怪的 “关键字” 叫做 this为什么说它是 奇奇怪怪 呢, 是因为你写出 100 个 this, 可能有 100 个解释, 完全不挨边,但是, 在你的学习过程中, 搞清楚了 this 这个玩意, 那么会对你的开发生涯有很大帮助的,接下来咱们就…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
