LeetCode 每日一题 ---- 【741.摘樱桃】
LeetCode 每日一题 ---- 【741.摘樱桃】
- 741.摘樱桃
- 方法:动态规划
741.摘樱桃
方法:动态规划
这是一道动态规划的题目,enmmmm,依旧是做不出来,尤其是看到困难两个标红的字体,就更不想做了,然后是看着答案一点一点顺着思路和题解做的,做完后发现也没有想象中的那么难
从(n-1, n-1)返回(0, 0)可以等价的看做又一次从(0, 0)到(n-1, n-1)的路径,
然后求一个所能采到樱桃个数的最大值
不妨假设两人同时出发,且速度相同。无论这两人怎么走,在时间相同的情况下,
他们向右走的步数加上向下走的步数之和是一个定值(设为 k)。
设两人的坐标为 (x1,y1)和 (x2,y2),则 x1+y1=x2+y2=k。
那么当 x1=x2 时,必然有 y1=y2,即两个人到达了同一个格子。
定义状态:f[k][x1][x2]
k表示两个人分别从(x1, k - x1)和(x2, k - x2)同时触发,到达(n-1, n-1)锁摘到樱桃个数之和
x1,x2分别代表第一个和第二个人的起始横坐标
状态转移方程:
f[k][x1][x2]可以由四种情况转移过来
都往右:f[k][x1][x2] = f[k-1][x1][x2]
A往下,B往右:f[k][x1][x2] = f[k-1][x1-2][x2]
A往右,B往下:f[k][x1][x2] = f[k-1][x1][x2-1]
都往下:f[k][x1][x2] = f[k-1][x1-1][x2-1]
f[k][x1][x2]的最终结果是上述四种情况的最大值,然后再累加上grid[x1][k-x1]和grid[x2][k-x2]就可以得到最终该位置的答案
若x1==x2说明第一个人和第二个人的位置重合了,所以在这种情况下,grid[x1][k-x1]只能加一次
/**
从(n-1, n-1)返回(0, 0)可以等价的看做又一次从(0, 0)到(n-1, n-1)的路径,
然后求一个所能采到樱桃个数的最大值
不妨假设两人同时出发,且速度相同。无论这两人怎么走,在时间相同的情况下,
他们向右走的步数加上向下走的步数之和是一个定值(设为 k)。
设两人的坐标为 (x1,y1)和 (x2,y2),则 x1+y1=x2+y2=k。
那么当 x1=x2 时,必然有 y1=y2,即两个人到达了同一个格子。
定义状态:f[k][x1][x2] k表示两个人分别从(x1, k - x1)和(x2, k - x2)同时触发,到达(n-1, n-1)锁摘到樱桃个数之和x1,x2分别代表第一个和第二个人的起始横坐标
状态转移方程:f[k][x1][x2]可以由四种情况转移过来都往右:f[k][x1][x2] = f[k-1][x1][x2]A往下,B往右:f[k][x1][x2] = f[k-1][x1-2][x2]A往右,B往下:f[k][x1][x2] = f[k-1][x1][x2-1]都往下:f[k][x1][x2] = f[k-1][x1-1][x2-1]f[k][x1][x2]的最终结果是上述四种情况的最大值,然后再累加上grid[x1][k-x1]和grid[x2][k-x2]就可以得到最终该位置的答案若x1==x2说明第一个人和第二个人的位置重合了,所以在这种情况下,grid[x1][k-x1]只能加一次*/
class Solution {public int cherryPickup(int[][] grid) {int n = grid.length;int[][][] f = new int[n * 2 - 1][n][n];// 初始化for (int i = 0; i < n * 2 - 1; i ++ ) {for (int j = 0; j < n; j ++ ) {Arrays.fill(f[i][j], Integer.MIN_VALUE);}}f[0][0][0] = grid[0][0];for (int k = 1; k < n * 2 - 1; k ++ ) {// 防止越界for (int x1 = Math.max(k - n + 1, 0); x1 <= Math.min(k, n - 1); x1 ++ ) {int y1 = k - x1;// 荆棘不可越过if (grid[x1][y1] == -1) {continue;}for (int x2 = x1; x2 <= Math.min(k, n - 1); x2 ++ ) {int y2 = k - x2;if (grid[x2][y2] == -1) {continue;}// 都往右int res = f[k - 1][x1][x2];// 往下,往右if (x1 > 0) {res = Math.max(res, f[k - 1][x1 - 1][x2]);}// 往右,往下if (x2 > 0) {res = Math.max(res, f[k - 1][x1][x2 - 1]);}// 都往下if (x1 > 0 && x2 > 0) {res = Math.max(res, f[k - 1][x1 - 1][x2 - 1]);}res += grid[x1][y1];if (x2 != x1) {res += grid[x2][y2];}f[k][x1][x2] = res;}}}return Math.max(f[n * 2 - 2][n - 1][n - 1], 0);}
}
时间复杂度:
O(n3)
空间复杂度:
O(n2)
相关文章:

LeetCode 每日一题 ---- 【741.摘樱桃】
LeetCode 每日一题 ---- 【741.摘樱桃】 741.摘樱桃方法:动态规划 741.摘樱桃 方法:动态规划 这是一道动态规划的题目,enmmmm,依旧是做不出来,尤其是看到困难两个标红的字体,就更不想做了,然后…...

新火种AI|挑战谷歌,OpenAI要推出搜索引擎?
作者:一号 编辑:美美 在AI革新的浪潮下,谷歌搜索迎来了越来越多的“挑战者”。 最近,据多家外媒的消息,有知情人士透露,OpenAI正计划上线一款基于ChatGPT的大型产品,将提供一个新的搜索引擎&…...

选择适用的无尘棉签:保障洁净生产环境下的高效擦拭
随着洁净生产条件的日益普及和无尘级别要求的提高,无尘擦拭用品成为广大用户追捧的必备工具。在这个领域,无尘棉签作为一种高效的擦拭工具,扮演着重要的角色。然而,面对市场上种类繁多的无尘棉签,如何选择最合适的产品…...
通信录的动态版本
一. 增加需求 在学习了动态开辟内存之后 我们对于通讯录产生了新的需求 要求我们做出一个动态增长的版本 即 随着我们储存联系人的增加 储存的空间增加 要求 : 1 初始空间为3 2 每次达到上限之后 扩容两个内存 二. 动手实施 我们首先要创建一个结构体 结构体…...

FineReport高频面试题及参考答案
FineReport是一款利用什么语言开发的报表工具? FineReport是一款基于Java语言开发的报表工具。Java是一种广泛使用的编程语言,特别适合于跨平台的软件开发。FineReport利用Java语言的诸多优势,如稳定性、安全性、可移植性和强大的网络功能&a…...

git merge 命令合并指定分支到当前分支
git merge 是一个用于合并两个分支的 Git 命令。当你在不同的分支上工作时,可能会有一些不同的更改。使用 git merge 可以将这些更改合并到一起。以下是一些常见的 git merge 用法示例: 1. 合并当前分支与另一个分支的更改 git merge <branch-name&…...
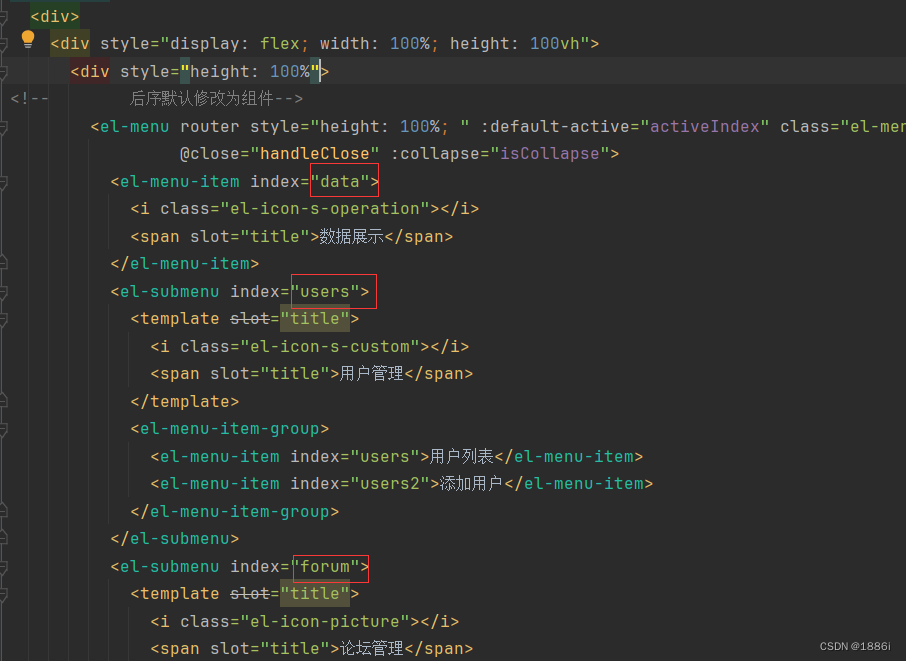
【在线OJ】Vue创建OJ管理系统
一、创建项目 vue ui命令创建项目 项目创建完成后来到项目 二、导航栏 首先创建一个根页面,让他展示在页面上 创建之后来到路由配置界面 然后安装ElementUI,来到官网找到导航栏 复制代码后粘贴到刚才创建的vue文件里,启动项目ÿ…...

常用算法汇总
作者:指针不指南吗 专栏:算法篇 🐾算法思维逻辑🐾 文章目录 1.判断闰年2.计算从某天到某天的天数3.二分4. 前缀和5.差分6.图论6.1dfs6.2走迷宫 7.最短路7.1dijkstra7.2foly 8.并查集9.数论9.1gcd lcm9.2判断素数(质数)9.3分解质因…...
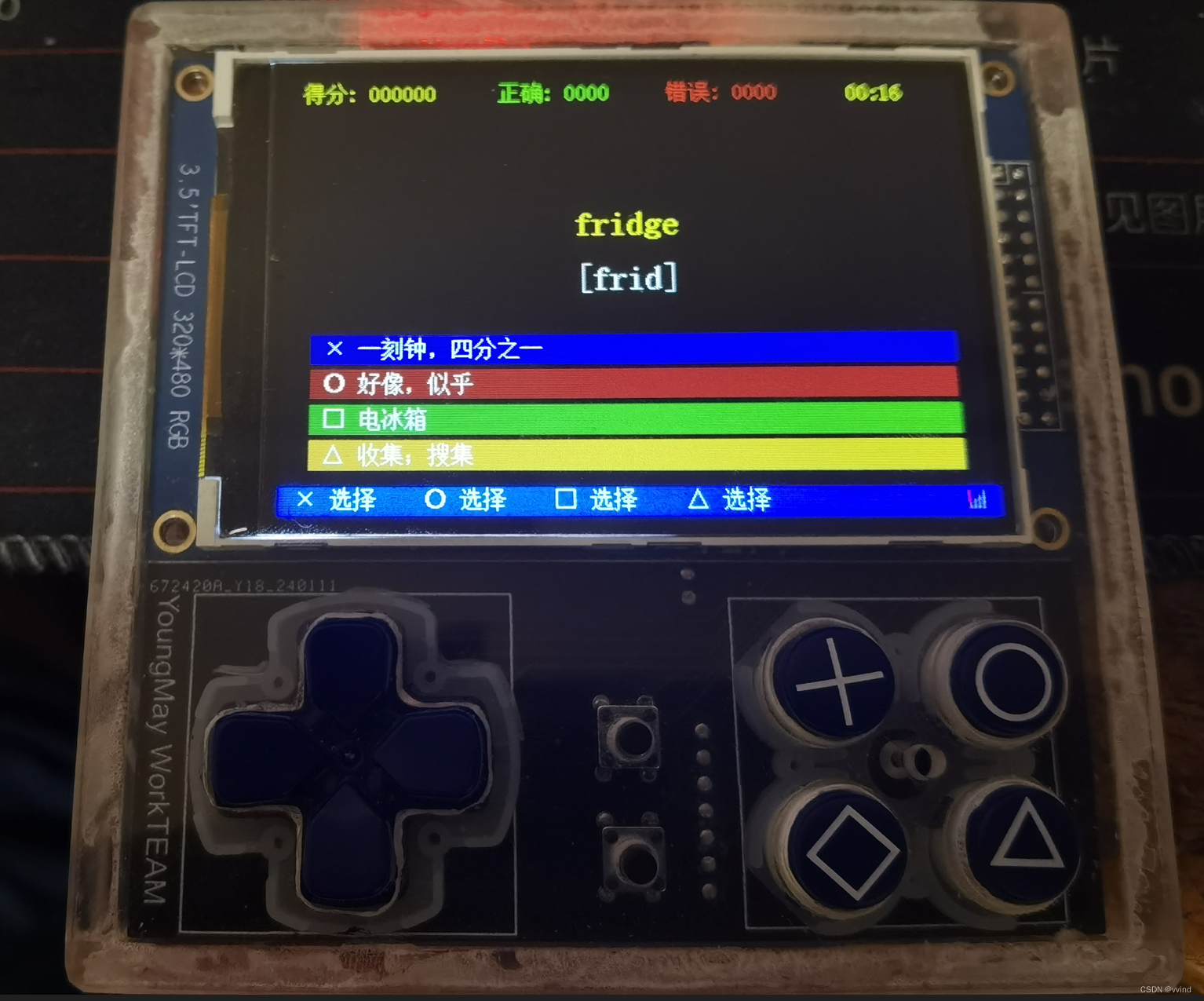
W801学习笔记二十二:英语背单词学习应用——下
续上篇: W801学习笔记二十一:英语背单词学习应用——上 五、处理用户交互 由于英语也是采用了和唐诗一样的《三分钟限时挑战》《五十题竞速挑战》《零错误闯关挑战》,所以用户交互的逻辑和唐诗是一样的。所以,我们抽一个基类&a…...

Vue路由的模式和原理
一、hash模式(默认) 使用URL的hash来模拟一个完整的URL,当URL发生改变时不会向服务器发起请求。# 和其后面的字符称为hash,可通过 window.location.hash 获取。当hash改变会触发(包括浏览器的前进、后退)会…...

在K8S中,静态、动态、自主式Pod有何区别
在Kubernetes(简称K8s)中,静态Pod、自主式Pod和动态Pod是不同管理方式下的Pod类型,它们的区别主要体现在创建和管理方式上: 静态Pod: 静态Pod是由kubelet直接管理的,其配置文件存储在节点本地而…...

【Three.js基础学习】15.scroll-based-animation
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 前言 课程要点 结合html等场景 做滚动动画 1.遇到的问题, 在向下滚动时,下方会显白(部分浏览器) 解决:alpha:true …...
ubantu安装mysql
安装 准备:下载:版本5.1.17的MySQL并上传至Ubuntu系统 #解压 tar -xvf mysql-server_5.7.17-1ubuntu16.10_amd64.deb-bundle.tar #提前安装插件 sudo apt-get install libaio1 libmecab2 #若安装失败使用以下命令 apt --fix-broken install sudo apt-g…...

注意!华为HCIP-Datacom认证考试题有变化!
01 注意 HCIP Datacom H12-831考试变题了,最近要考试的多观望一下,821目前稳定。 华为HCIP考试以后要加难度,增加实验题,还没考完的小伙伴抓紧时间了。 02 华为HCIP认证大更新 未来将增加实验考试,拒绝背题库的Pass&a…...

你是我的荣耀 | 林先生:从酷爱数学到毕业走向数据分析岗位
人物背景: 研究生国家奖学金、本科生国家奖学金、学业奖学金一等奖、上海市优秀毕业生; 应用统计专业 CPDA优秀学员 ## 为什么选择数据分析相关专业 我是应用统计专业的一个应届毕业生,目前在一家上海市属的国企,从事数据分析相关…...

操作系统真象还原-bochs安装
今天读了《操作系统真象还原》这本书,写上比较幽默通俗。书中例子需要安装一个bochs系统,记录一下安装过程。参考了书中1.4,1.5两节,书中尽让有两处问题,也记录了下来。 1.3 操作系统的宿主环境 下载地址:…...
windows平台安装labelme
之前写过一篇文章也是关于在windows平台安装labelme的:《windows平台python版labelme安装与使用_labelme下载-CSDN博客》,随着软件与工具的更新换代,按照同样的方法最近在使用的时候出现了错误,出现创建虚拟环境失败,具…...
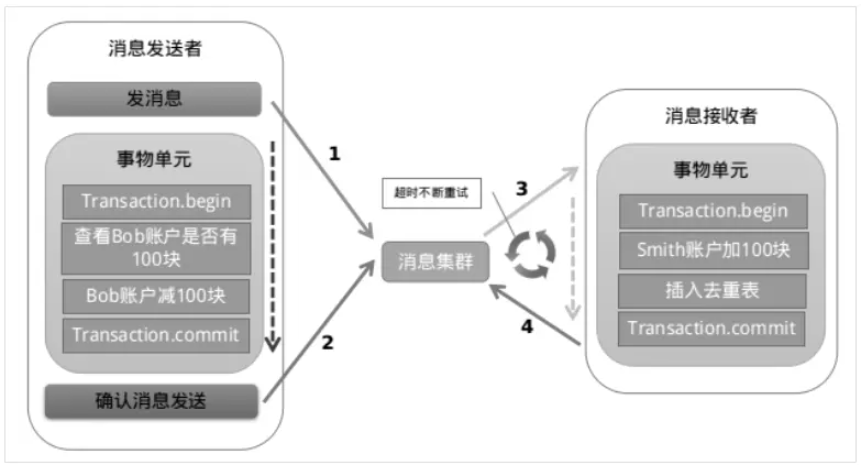
微服务之SpringCloud AlibabaSeata处理分布式事务
一、概述 1.1背景 一次业务操作需要跨多个数据源或需要跨多个系统进行远程调用,就会产生分布式事务问题 but 关系型数据库提供的能力是基于单机事务的,一旦遇到分布式事务场景,就需要通过更多其他技术手段来解决问题。 全局事务:…...
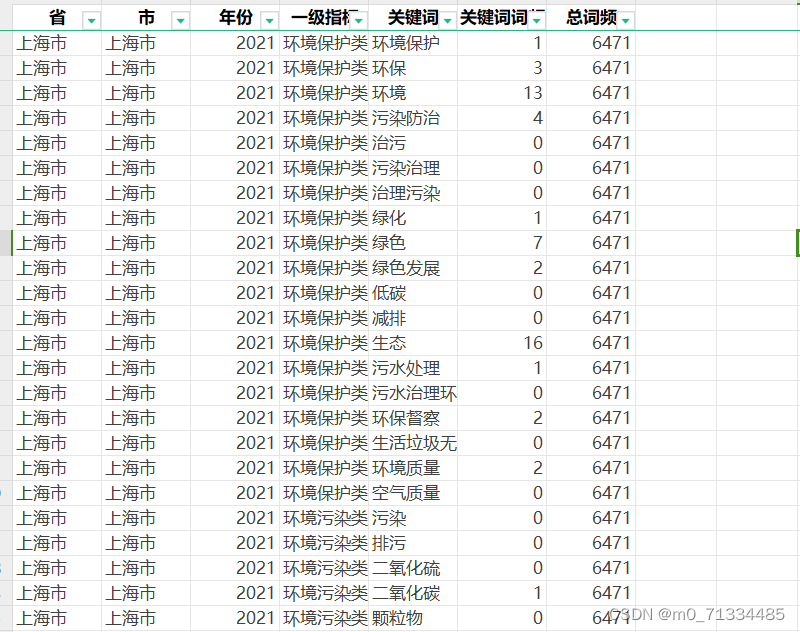
2005-2021年全国各地级市生态环境注意力/环保注意力数据(根据政府报告文本词频统计)
2005-2021年全国各地级市生态环境注意力/环保注意力数据(根据政府报告文本词频统计) 2005-2021年全国各地级市生态环境注意力/环保注意力数据(根据政府报告文本词频统计) 1、时间:2005-2021年 2、范围:2…...

熟悉这些道理可以让人更好地应对各种挑战和困难。
1. 为别人尽最大的力量,最后就是为自己尽最大的力量。——罗斯金 2. 世上有一条永恒不变的法则:当你不在乎,你就得到。当你变好,你才会遇到更好的。只有当你变强大,你才不害怕孤单。当你不害怕孤单,你才能够宁缺毋滥。…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
