Verilog语法之数学函数
Verilog-2005支持一些简单的数学函数,其参数的数据类型只能是integer和real型。
Integer型数学函数
$clog2是一个以2为底的对数函数,其结果向上取整,返回值典型的格式:
integer result;
result = $clog2(n);
最典型的应用就是通过参数化的方式来求某个变量的位宽,在另一篇文章已经对用法做了详细的介绍:Verilog设计中如何匹配变量的位宽?($clog2系统函数)
Real型数学函数
其参数数据类型为real型,返回值同样为real型,这意味着下面这些数学函数都无法被综合:
| Function | Description |
|---|---|
| $ln(x) | N自然对数(以e为底的对数) |
| $log10(x) | 十进制对数(以10为底的对数) |
| exp(x) | e^x ,e=2.718281828... |
| sqrt(x) | 开平方 |
| $pow(x, y) | x^y |
| $floor(x) | 向下取整 |
| $ceil(x) | 向上取整 |
| $hypot(x, y) | sqrt(xx + yy)。对两个数平方和开平方 |
| $sin(x) | sin |
| $cos(x) | cos |
| $tan(x) | tan |
| $asin(x) | arcsin |
| $acos(x) | arccos |
| $atan(x) | arccos |
| $atan2(x, y) | x/y的反正切 |
| $sinh(x) | 双曲正弦 |
| $cosh(x) | 双曲余弦 |
| $tanh(x) | 双曲正切 |
| $asinh(x) | 反双曲正弦 |
| $acosh(x) | 反双曲余弦 |
| $atanh(x) | 反双曲正切 |
写个简单的testbench到modelsim验证一下:
module tb_math_fuc;real x, y; //这些函数的参数需要是real类型,返回也是real类型initial begin //0.3f表示取小数点后3位,下同x = 10000;$display("$log10(%0.3f) = %0.3f", x, $log10(x)); //以10为底的对数 x = 1;$display("$ln(%0.3f) = %0.3f", x, $ln(x)); //以e为底的对数x = 2;$display("$exp(%0.3f) = %0.3f", x, $exp(x)); //e^xx = 25;$display("$sqrt(%0.3f) = %0.3f", x, $sqrt(x)); //开平方x = 5;y = 3;$display("$pow(%0.3f, %0.3f) = %0.3f", x, y, $pow(x, y)); //x^yx = 2.7813;$display("$floor(%0.3f) = %0.3f", x, $floor(x)); //向下取整x = 7.1111;$display("$ceil(%0.3f) = %0.3f", x, $ceil(x)); //向上取整x = 30 * (22.0/7.0) / 180;$display("$sin(%0.3f) = %0.3f", x, $sin(x)); //sin函数x = 90 * (22.0/7.0) / 180;$display("$cos(%0.3f) = %0.3f", x, $cos(x)); //cos函数x = 45 * (22.0/7.0) / 180;$display("$tan(%0.3f) = %0.3f", x, $tan(x)); //tan函数x = 0.5;$display("$asin(%0.3f) = %0.3f rad, %0.3f deg", x, $asin(x), $asin(x) * 7.0/22.0 * 180);//arcsin函数x = 0;$display("$acos(%0.3f) = %0.3f rad, %0.3f deg", x, $acos(x), $acos(x) * 7.0/22.0 * 180); //arccos函数x = 1;$display("$atan(%0.3f) = %0.3f rad, %f deg", x, $atan(x), $atan(x) * 7.0/22.0 * 180); //arctan函数endendmodule这是验证结果:
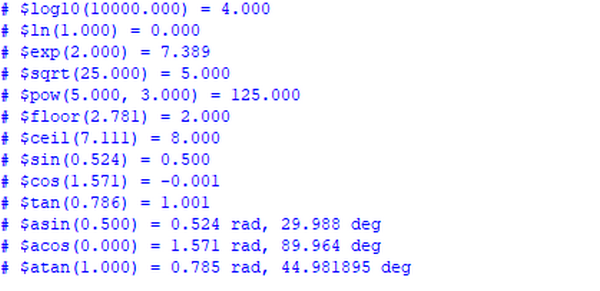
相关文章:

Verilog语法之数学函数
Verilog-2005支持一些简单的数学函数,其参数的数据类型只能是integer和real型。 Integer型数学函数 $clog2是一个以2为底的对数函数,其结果向上取整,返回值典型的格式: integer result; result $clog2(n); 最典型的应用就是通过…...
)
【手撕面试题】JavaScript(高频知识点一)
目录 面试官:请你简述 var、let、const 三者之间的区别? 面试官:请你谈谈对深拷贝与浅拷贝的理解 面试官:输入URL的那一瞬间浏览器做了什么? 面试官:说一说cookie sessionStorage localStorage 区别&am…...
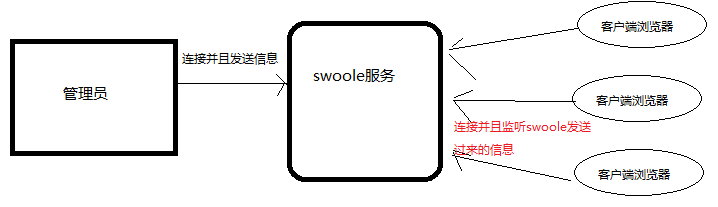
如何用PHP实现消息推送
什么是消息推送 通过服务器自动推送消息到客户端(浏览器,APP,微信)的应用技术。 2. 为什么要使用消息推送技术 通常情况下都是用户发送请求浏览器显示用户需要的信息。推送技术通过自动传送信息给用户,来减少用于网络上搜索的时间。它根据…...
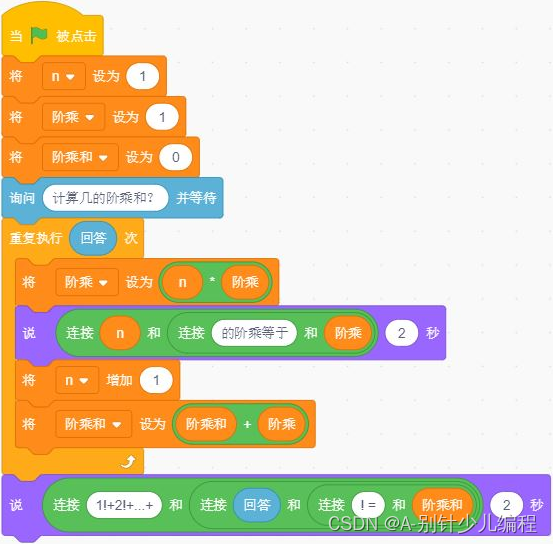
电子学会2020年6月青少年软件编程(图形化)等级考试试卷(四级)答案解析
青少年软件编程(Scratch)等级考试试卷(四级A卷) 分数:100.00 题数:30 一、单选题(共15题,每题2分,共30分) 1. 执行下图程序后,“花名…...

DaVinci:调色版本
调色版本 Grade Version记录着片段的全部调色信息。将一种调色风格或效果,保存为一个调色版本,从而可在多个调色版本之间查看、比较、挑选或者渲染输出。调色版本类型本地版本Local Versions在没有创建新的调色版本之前,片段的调色信息默认记…...
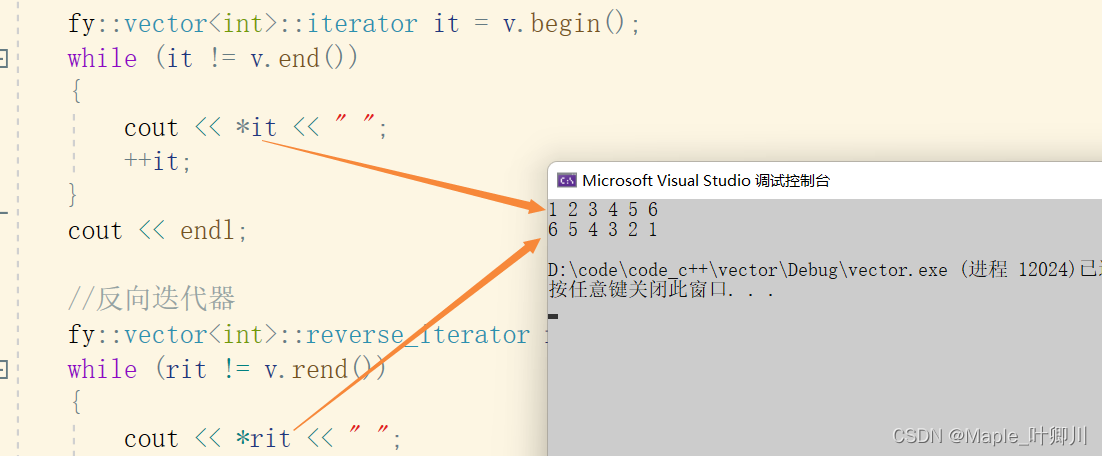
【C++初阶】十二、STL---反向迭代器的实现
目录 一、反向迭代器 二、反向迭代器的实现 一、反向迭代器 之前的模拟实现vector、list 的时候,这些都是实现了正向迭代器,反向迭代器都没有实现,这里就要实现反向迭代器 反向迭代器也是适配器(配接器)的一种&#…...

day 43|● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉碎的可能结果…...
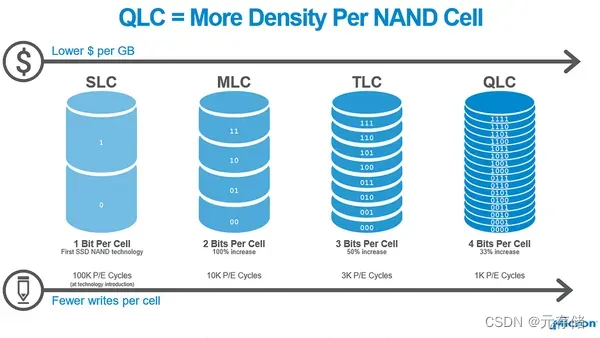
[SSD固态硬盘技术 0] SSD的结构和原理导论
版权声明: 本文禁止转载机械硬盘的存储系统由于内部结构,其IO访问性能无法进一步提高,CPU与存储器之间的性能差距逐渐扩大。以Nand Flash为存储介质的固态硬盘技术的发展,性能瓶颈得到缓解。1. 什么是SSD固态硬盘(Solid State Drives…...

Vue (3)
文章目录1. 数据代理1.1 回顾1.2 开始2. 事件处理2.1 v-on:click 点击事件2.2 事件修饰符2.3 键盘事件3. 计算属性3.1 插值语法实现3.2 methods实现3.3 计算属性实现4. 监视属性4.1 深度监视4.2 监视属性的简写形式4.3 watch 与 computed 对比1. 数据代理 在学习 数据代理 时 先…...

SQL语句,常用的DDL表操作语句
-- ddl sql 语句 -- 创建表 create table user_t( id int primary key auto_increment, -- 自增主键 name varchar(50) ); -- 查看表结构 desc user_t; desc user_test; -- 重命名表 alter table user_t rename to user_test; -- 查询数据库表 show tables; -- 添…...

C 语言 宏定义 :字符串化 stringify 的应用
字符串化 通过C 语言的宏(MICRO),可以把数值或者一段字符的组合,转换为字符串。 因为 C语言的宏在【预处理】阶段就展开了,所以可以实现一些比较使用的功能,比如一些数据的初始化操作 比如定义一个宏&…...

代替swagger的api接口神器
自动化API文档-APIFOX 文章作者:老杨 一:概述 大家在后端开发开发过程中,最痛恨的两天事情:1.写文档,2.别人不写文档。而我们后端开发,必定经历的事情就是要和前端&测试对接,我们需要把我…...

2月12日,30秒知全网,精选7个热点
///北京首批29家药店开通异地参保直接结算服务试点药店已覆盖北京市东城区、西城区、朝阳区、海淀区、丰台区和石景山区,为来京就医的外省市参保人员提供便利///杭州召开平台经济健康高质量发展座谈会落实更有针对性的政策供给、提供“店小二”“保姆式”服务、建立…...

HTML img和video object-fit 属性
简介 Css中object-fit主要是应用到img标签和Video标签的,来控制显示缩放效果的。 首先我们存在一张图片,原始图片的尺寸是 1080px x 600px, 展示效果如下: 如果我们的css样式中的img大小设定并不能满足图片的原始大小,比如我们的…...

Pascal版本的 - freopen
参数 filename -- 这是包含要打开的文件的名称的字符串。 mode -- 这是包含文件访问模式的字符串。它包括 - 高级编号模式&说明1个 “r” 打开文件进行读取。该文件必须存在。 2个 “w” 创建一个用于写入的空文件。如果已存在同名文件,则删除其内容并将该文件…...
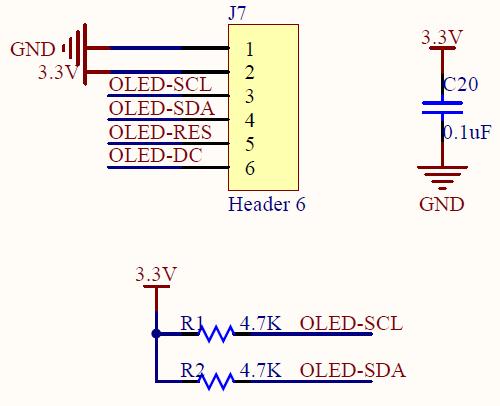
STM32单片机OLED显示
OLED接口电路STM32单片机OLED显示程序源代码#include "sys.h"#define OLED_RST_Clr() PCout(13)0 //RST#define OLED_RST_Set() PCout(13)1 //RST#define OLED_RS_Clr() PBout(4)0 //DC#define OLED_RS_Set() PBout(4)1 //DC#define OLED_SCLK_Clr()PCout(15)0 //SCL…...
备战金三银四,软件测试面试题(全)
1.B/S架构和C/S架构区别 B/S 只需要有操作系统和浏览器就行,可以实现跨平台,客户端零维护,维护成本低,但是个性化能力低,响应速度较慢 C/S响应速度快,安全性强,一般应用于局域网中,因…...

硬件篇-配置
机箱->239元 机箱选用的itx迷你机箱,为了后期nas方便拓展选了4盘位,该机箱还是比较符合我的预期的,颇有种麻雀虽小五脏俱全的感觉,机箱可以安装matx主板和itx主板,还是比较方便的,机箱带三个大散热风扇&…...

网页内容 中文乱码 解决办法
原因 是因为没有网页没有设置charset是utf-8 解决办法 <!DOCTYPE html> <html lang"en"><head><!-- 这一个标签不能少 --><meta charset"UTF-8" /><body></body> </html>...
【C++之容器篇】造轮子:模拟实现vector类
目录前言一、项目结构1. vector的简介2. 项目结构二、vector的底层结构三、默认成员函数(Member functions)1. 构造函数(1)无参构造函数(2)使用n个值来构造对象(3)使用一段迭代器区间来进行初始化(4)测试构造函数2. 拷贝构造函数(现代写法)3. 析构函数4.…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
