【数学建模】天然肠衣搭配问题
2011高教社杯全国大学生数学建模竞赛D题
天然肠衣(以下简称肠衣)制作加工是我国的一个传统产业,出口量占世界首位。肠衣经过清洗整理后被分割成长度不等的小段(原料),进入组装工序。传统的生产方式依靠人工,边丈量原料长度边心算,将原材料按指定根数和总长度组装出成品(捆)。
原料按长度分档,通常以0.5米为一档,如:3-3.4米按3米计算,3.5米-3.9米按3.5米计算,其余的依此类推。表1是几种常见成品的规格,长度单位为米,∞表示没有上限,但实际长度小于26米。
\space \space \space \space \space \space \space 表1 成品规格表
| 最短长度 | 最大长度 | 根数 | 总长度 |
|---|---|---|---|
| 3 | 6.5 | 20 | 89 |
| 7 | 13.5 | 8 | 89 |
| 14 | ∞ ∞ ∞ | 5 | 89 |
为了提高生产效率,公司计划改变组装工艺,先丈量所有原料,建立一个原料表。表2为某批次原料描述。

根据以上成品和原料描述,设计一个原料搭配方案,工人根据这个方案“照方抓药”进行生产。
公司对搭配方案有以下具体要求:
(1) 对于给定的一批原料,装出的成品捆数越多越好;
(2) 对于成品捆数相同的方案,最短长度最长的成品越多,方案越好;
(3) 为提高原料使用率,总长度允许有
天然肠衣搭配问题
- 提出假设
- 问题简单复述:
- 对应每一个任意种类的成品建立第一种模型
- 基于成品分配方案的第二种模型
- 模型二总结
- 手动实现局部最优解
- 局部最优解
提出假设
假设降级使用仅可降一级,不可多级降,如如长度为14米的原料不可以和长度介于3-6.5米的进行捆扎
问题简单复述:
用以0.5米为一档给出的原料按指定根数和总长度组装出成品,为此设计一个原料搭配方案。
方案好坏比较首先是装出的成品捆数越多越好;其次捆数相同的方案,最短长度为14的成品越多,方案越好
使用附带原则有总长度允许有 ± 0.5 ± 0.5 ±0.5米的误差,总根数允许比标准少 1 1 1根;某种规格对应原料如果出现剩余,可以降级使用。
建立数学模型:
首先考虑装出的成品捆数,设三种不同最短长度(从小到大)的成品个数依次为 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3
装出的成品捆数越多越好有:
m a x = ∑ 1 ≤ i ≤ 3 x i max = \sum_{1 \le i \le 3} x_i max=∑1≤i≤3xi
为了简化问题,解决最短长度为14的成品越多,方案越好的方案为:
设已求得一组可行解 x 1 ′ , x 2 ′ , x 3 ′ x_1',x_2',x_3' x1′,x2′,x3′
加入限制条件
x 3 > x 3 ′ x_3 > x_3' x3>x3′
考虑原料如果出现剩余,可以降级使用。那么解决顺序应该是成品三,成品二,成品一。
因为每个成品最短长度到最长长度的区间没有重叠,所以三个成品可以分开讨论。
对应每一个任意种类的成品建立第一种模型
设原料按长度由小到大的使用个数依次为 y 1 , y 2 , . . . , y n y_1 ,y_2 ,...,y_n y1,y2,...,yn,总长度为 a a a,根数为 b i ′ b_{i'} bi′,最小大长度 c i ′ c_{i'} ci′,最大长度 c j ′ c_{j'} cj′
都要满足
成品总长度在标准的 ± 0.5 ± 0.5 ±0.5米误差范围内:
a − 0.5 ≤ ( 3 + 0.5 ( i − 1 ) ) y i + ( 3 + 0.5 i ) y i + 1 + . . . ( 3 + 0.5 ( j − 1 ) ) y j ≤ a + 0.5 a-0.5 \le (3+0.5(i-1))y_i+(3+0.5i)y_{i+1}+...(3+0.5(j-1))y_j \le a+0.5 a−0.5≤(3+0.5(i−1))yi+(3+0.5i)yi+1+...(3+0.5(j−1))yj≤a+0.5
总根数和标准一致或总根数比标准少 1 1 1根:
y i + y i + 1 + . . . + y j = b i ′ − z , z = 0 / 1 y_i + y_{i+1} + ... +y_j = b_{i'}-z , z = 0/1 yi+yi+1+...+yj=bi′−z,z=0/1
使用的原料长度在成品规格表的标准长度范围内
2 ( c i ′ − 3 ) − 1 ≤ y k ≤ 2 ( c j ′ − 3 ) − 1 , i ≤ k ≤ j 2(c_{i'} - 3) -1 \le y_k\le 2(c_{j'} - 3) -1 , i\le k \le j 2(ci′−3)−1≤yk≤2(cj′−3)−1,i≤k≤j
考虑原料如果出现剩余,可以降级使用。我们设上一级(如果有的话)的的最大长度为 c j ′ + 1 c_{j'+1} cj′+1
2 ( c i ′ − 3 ) − 1 ≤ y k ≤ 2 ( c j ′ + 1 − 3 ) − 1 , i ≤ k ≤ j 2(c_{i'} - 3) -1 \le y_k\le 2(c_{j'+1} - 3) -1 , i\le k \le j 2(ci′−3)−1≤yk≤2(cj′+1−3)−1,i≤k≤j
因为做出一个成品,对应使用的原料数量会降低,设原料按长度由小到大的减少总个数依次为 u 1 , u 2 , . . . , u n u_1 ,u_2 ,...,u_n u1,u2,...,un,原料按长度由小到大的总个数依次为 d 1 d 2 , . . . , d n d_1 d_2 ,...,d_n d1d2,...,dn
我们要满足每一次原料都不能凭空产生
y i ≤ d i − u i , 1 ≤ i ≤ n y_i \le d_i - u_i ,1 \le i \le n yi≤di−ui,1≤i≤n
并且当满足 { a − 0.5 ≤ ( 3 + 0.5 ( i − 1 ) ) y i + ( 3 + 0.5 i ) y i + 1 + . . . ( 3 + 0.5 ( j − 1 ) ) y j ≤ a + 0.5 y i + y i + 1 + . . . + y j = b i − z , z = 0 / 1 2 ( c i ′ − 3 ) − 1 ≤ y k ≤ 2 ( c j ′ + 1 − 3 ) − 1 , i ≤ k ≤ j y i ≤ d i − u i , 1 ≤ i ≤ n \begin{cases} a-0.5 \le (3+0.5(i-1))y_i+(3+0.5i)y_{i+1}+...(3+0.5(j-1))y_j \le a+0.5\\ y_i + y_{i+1} + ... +y_j = b_i-z , z = 0/1 \\ 2(c_{i'} - 3) -1 \le y_k\le 2(c_{j'+1} - 3) -1 , i\le k \le j \\ y_i \le d_i - u_i ,1 \le i \le n \end{cases} ⎩ ⎨ ⎧a−0.5≤(3+0.5(i−1))yi+(3+0.5i)yi+1+...(3+0.5(j−1))yj≤a+0.5yi+yi+1+...+yj=bi−z,z=0/12(ci′−3)−1≤yk≤2(cj′+1−3)−1,i≤k≤jyi≤di−ui,1≤i≤n的时候对应种类的成品数量加一,即 x i = x i + 1 x_i=x_i+1 xi=xi+1,并且原材料使用后对应的原材料数目减少,即 u i = u i + y i , 1 ≤ i ≤ n u_i =u_i+y_i , 1 \le i \le n ui=ui+yi,1≤i≤n
C++
#include <iostream>
#include <vector>
#include <array>
using namespace std;
int cnt[] ={43,59,39,41,27,28,34,21,24,24,20,25,21,23,21,18,31,23,22,59,18,25,35,29,30,42,28,42,45,49,50,64,52,63,49,35,27,16,12,2,0,6,0,0,0,1}; // 3+0.5i
int x[4];
int x_3 = 0;//已知x3的最大解
void solve();double min_size = 3,max_size =6.5,total_size =89;
int roots_Number = 20;
int f_xi = 1;double now_total_size=0;
int now_roots_Number = 0;
void f( int k ,int u){if(now_total_size <= 0.5 + total_size && now_total_size >= total_size - 0.5){if(now_roots_Number == roots_Number || now_roots_Number == roots_Number-1){x[f_xi] = max(x[f_xi],u+1);double kt = now_total_size;int kr = now_roots_Number;now_total_size = now_roots_Number = 0;f(((int)max_size - 3)*2,u+1);now_total_size = kt , now_roots_Number = kr;return ;}else return ;}//if(now_total_size>0.5 + total_size)return ; // cut down
#if 0 //small to bigif(3+0.5*k > max_size)return ; // can't choseint ct = min(cnt[k] ,(int)((total_size - now_total_size)/(3+0.5*k)));for(int i=0;i<=ct;i++){cnt[k]-=i;f(now_total_size+i*(3+0.5*k) , now_roots_Number+i ,k+1,u );cnt[k]+=i;}
#endif
#if 1 // big to smallif(3+0.5*k < min_size)return ; // can't choseint ct = min(cnt[k] ,(int)((total_size - now_total_size)/(3+0.5*k)));ct = min(ct,roots_Number - now_roots_Number);//if(now_roots_Number > roots_Number)return ;for(int i=0;i<=ct;i++){cnt[k]-=i;now_total_size += i*(3+0.5*k);now_roots_Number+=i;f(k-1,u);now_total_size -= i*(3+0.5*k);now_roots_Number-=i;cnt[k]+=i;}
#endif
}void solve(){//排除要求四/*min_size = 3,max_size =6.5,total_size =89;roots_Number = 20;f_xi = 1;now_total_size=0;now_roots_Number = 0;f(((int)max_size - 3)*2,0);//3+0.5*k = min_size//k = (min_size - 3) / 0.5min_size = 7,max_size =13.5,total_size =89;roots_Number = 8;f_xi = 2;now_total_size=0;now_roots_Number = 0;f(((int)max_size - 3)*2,0);*/min_size = 14,max_size =25.5,total_size =89;roots_Number = 5;f_xi = 3;now_total_size=0;now_roots_Number = 0;f((max_size - 3)*2,0);cout << x[3];
}int main() {solve();return 0;
}基于成品分配方案的第二种模型
考虑到第一种模型跑程序时候,就算剪枝也会跑许多多余的分支,考虑到本题是分配问题,并且每一种成品规格限制比较死,所以我们可以列出该成品分配的所有方案。
可以自行运行一下程序查看所有方案,对应成品三有1823种
C++
#include <iostream>
#include <vector>
#include <array>
using namespace std;
int cnt[46] ={43,59,39,41,27,28,34,21,24,24,20,25,21,23,21,18,31,23,22,59,18,25,35,29,30,42,28,42,45,49,50,64,52,63,49,35,27,16,12,2,0,6,0,0,0,1}; // 3+0.5i
int x[4];
int x_3 = 0;//已知x3的最大解
void solve();double min_size = 3,max_size =6.5,total_size =89;
int roots_Number = 20;
int f_xi = 1;double now_total_size=0;
int now_roots_Number = 0;
int bt = 1;
int a[46];
void f( int k ,int u){if(now_total_size <= 0.5 + total_size && now_total_size >= total_size - 0.5){if(now_roots_Number == roots_Number || now_roots_Number == roots_Number-1){cout << "\n\n方案" << bt << ":\n|";int kk = 0;for(int i=0;i<=45;i++){if(a[i]){cout << 3+0.5*i << '|';kk++;}}cout << "\n|";for(int i=0;i<kk;i++){cout << "--|";}cout << "\n|";for(int i=0;i<=45;i++){if(a[i])cout << a[i] << '|';}bt++;return ;}else return ;}//if(now_total_size>0.5 + total_size)return ; // cut down
#if 0 //small to bigif(3+0.5*k > max_size)return ; // can't choseint ct = min(cnt[k] ,(int)((total_size - now_total_size)/(3+0.5*k)));for(int i=0;i<=ct;i++){cnt[k]-=i;f(now_total_size+i*(3+0.5*k) , now_roots_Number+i ,k+1,u );cnt[k]+=i;}
#endif
#if 1 // big to smallif(3+0.5*k < min_size)return ; // can't choseint ct = min(cnt[k] ,(int)((total_size - now_total_size)/(3+0.5*k)));ct = min(ct,roots_Number - now_roots_Number);//if(now_roots_Number > roots_Number)return ;for(int i=0;i<=ct;i++){cnt[k]-=i;now_total_size += i*(3+0.5*k);now_roots_Number+=i;a[k]+=i;f(k-1,u);now_total_size -= i*(3+0.5*k);now_roots_Number-=i;cnt[k]+=i;a[k]-=i;}
#endif
}void solve(){//排除要求四/*min_size = 3,max_size =6.5,total_size =89;roots_Number = 20;f_xi = 1;now_total_size=0;now_roots_Number = 0;f(((int)max_size - 3)*2,0);//3+0.5*k = min_size//k = (min_size - 3) / 0.5min_size = 7,max_size =13.5,total_size =89;roots_Number = 8;f_xi = 2;now_total_size=0;now_roots_Number = 0;f(((int)max_size - 3)*2,0);*/min_size = 14,max_size =25.5,total_size =89;roots_Number = 5;f_xi = 3;now_total_size=0;now_roots_Number = 0;f((max_size - 3)*2,0);}int main() {solve();return 0;
}下面列出其中几个方案
方案1:
| 17.5 | 18 |
|---|---|
| 3 | 2 |
方案2:
| 17 | 17.5 | 18 |
|---|---|---|
| 1 | 1 | 3 |
方案3:
| 17.5 | 18 |
|---|---|
| 2 | 3 |
方案1467:
| 14 | 14.5 | 16 | 21.5 | 22.5 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
方案1653:
| 14 | 14.5 | 15 | 21.5 | 23.5 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
方案1800:
| 20 | 20.5 | 22.5 | 25.5 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
方案1823:
| 16.5 | 23.5 | 25.5 |
|---|---|---|
| 1 | 2 | 1 |
列出该成品分配的所有方案后,设计第二种模型:
设使用方案 i i i的次数为 y i y_i yi,原料按长度由小到大的总个数依次为 d 1 d 2 , . . . , d n d_1 d_2 ,...,d_n d1d2,...,dn
方案总数为 a a a;方案 i i i使用第 j j j种原料数量为 z i j z_{ij} zij
对于每一个原料我们都得
d i ≥ ∑ 1 ≤ j ≤ a y j ∗ z j i , 1 ≤ i ≤ n d_i \ge \sum_{1 \le j \le a} y_j*z_{ji} , 1\le i \le n di≥∑1≤j≤ayj∗zji,1≤i≤n
求 max ∑ 1 ≤ i ≤ a y i \max \sum_{1\le i \le a}y_i max∑1≤i≤ayi
对于成品三:
Lingo
sets:aa/1..46/:d;bb/1..1823/:y;cc(bb,aa):z;
endsets
data:d = 43,59,39,41,27,28,34,21,24,24,20,25,21,23,21,18,31,23,22,59,18,25,35,29,30,42,28,42,45,49,50,64,52,63,49,35,27,16,12,2,0
,6,0,0,0,1;enddata
max = @sum(bb(i):y(i));
@for(bb(i):@gin(y(i)));
@for(bb(i):y(i)>0);
@for(aa(i):d(i)>@sum(bb(j):y(j)*z(j,i)));
将下面C++程序运行结果带入上面Lingo中 , 在data: enddata 里面加 z = …
#include <iostream>
#include <vector>
#include <array>
using namespace std;
int cnt[46] ={43,59,39,41,27,28,34,21,24,24,20,25,21,23,21,18,31,23,22,59,18,25,35,29,30,42,28,42,45,49,50,64,52,63,49,35,27,16,12,2,0,6,0,0,0,1}; // 3+0.5i
void solve();double min_size = 3,max_size =6.5,total_size =89;
int roots_Number = 20;
double now_total_size=0;
int now_roots_Number = 0;
int bt = 1;
int a[46];
void f( int k ,int u){if(now_total_size <= 0.5 + total_size && now_total_size >= total_size - 0.5){if(now_roots_Number == roots_Number || now_roots_Number == roots_Number-1){//方案数在后for(int i=0;i<=45;i++){//cout << "z(" << i << "," << bt << ")=" << a[i] << '\n';cout << a[i] << ",";}bt++;return ;}else return ;}if(3+0.5*k < min_size)return ; // can't choseint ct = min(cnt[k] ,(int)((total_size - now_total_size)/(3+0.5*k)));ct = min(ct,roots_Number - now_roots_Number);//if(now_roots_Number > roots_Number)return ;for(int i=0;i<=ct;i++){cnt[k]-=i;now_total_size += i*(3+0.5*k);now_roots_Number+=i;a[k]+=i;f(k-1,u);now_total_size -= i*(3+0.5*k);now_roots_Number-=i;cnt[k]+=i;a[k]-=i;}
}void solve(){min_size = 14,max_size =25.5,total_size =89;roots_Number = 5;f_xi = 3;now_total_size=0;now_roots_Number = 0;f((max_size - 3)*2,0);
}int main() {solve();return 0;
}Lingo求解得
Objective value: 137.0000
Objective bound: 137.0000
修改一下Lingo,添加下面这一行可以查看剩余原料数量
@for(aa(i):u(i) = d(i)-@sum(bb(j):y(j)*z(j,i)));
同上处理成品一二得到最终程序
Lingo
sets:aa/1..46/:d,u,v;bb/1..1823/:y;cc(bb,aa):z;dd/1..466598/:x;ee(dd,aa):e;ff/1..2861814/:fgg(ff,aa):h;
endsets
data:d = 43,59,39,41,27,28,34,21,24,24,20,25,21,23,21,18,31,23,22,59,18,25,35,29,30,42,28,42,45,49,50,64,52,63,49,35,27,16,12,2,0
,6,0,0,0,1;enddata
!成品三
!max = @sum(bb(i):y(i));
@sum(bb(i):y(i)) > 137;
@for(bb(i):@gin(y(i)));
@for(bb(i):y(i)>0);
@for(aa(i):d(i)>@sum(bb(j):y(j)*z(j,i)));
@for(aa(i):u(i) = d(i)-@sum(bb(j):y(j)*z(j,i)));
!成品二
@sum(dd(i):x(i)) > ...;!求成品三后成品二最大组成数量+@for(dd(i):@gin(x(i)));
@for(dd(i):x(i)>0);
@for(aa(i):u(i)>@sum(dd(j):x(j)*e(j,i)));
@for(aa(i):v(i) = d(i)-@sum(dd(j):x(j)*e(j,i)));
!成品一
@for(ff(i):@gin(f(i)));
@for(ff(i):f(i)>0);
@for(aa(i):v(i)>@sum(ff(j):f(j)*h(j,i)));
max = @sum(bb(i):y(i)) + @sum(dd(j):x(j)) + @sum(dd(j):x(j));
需要在C++/其他程序中跑出成品一的2861814种方案的列表和成品二的466598种方案的列表。加在上述代码中。或者用其他方式给e和f赋值
e = ... !成品二的方案
h = ... !成品一的方案
模型二总结
思路总结:配完成品三,得出剩余的原材料数量,再配成品二,得出剩余原材料数量,最后配成品一。最后得到最优配比
目前的问题:无法有效的解决剩余这个关键,剩余条件为剩下的无法组成任何一种成品方案。
仅靠代码@sum(bb(i):y(i)) > 137;去约束剩余这个条件,只是局部最优,而不一定是全局最优
代码优化思路:例如成品三对于前面20多个都没用,直接优化掉;成品二一同上
难点:目前已知成品一方案数多达百万量级
手动实现局部最优解
虽然得出的答案不一定是全局最优,但可以先试试手动模拟成品三,二,一的步骤,先得出一种(多种)局部最优。如果有规律或者新的上限模型,就可以推出某一个局部最优解即是全局最优
按照模型二跑一次成品三
Objective value: 137.0000Objective bound: 137.0000U( 30) 1.000000 0.000000
长度范围为 17.5 − 17.9 17.5-17.9 17.5−17.9剩余1根
将剩余的长度的带入,得出成品二的分配方案有12729种,相比于带入无处理成品三后数据的直接计算的分配方案少了一个量级。
将成品二的分配方案带入模型和程序中得:
Objective value: 37.00000Objective bound: 37.00000U( 1) 43.00000 0.000000U( 2) 59.00000 0.000000U( 3) 39.00000 0.000000U( 4) 41.00000 0.000000U( 5) 27.00000 0.000000U( 6) 28.00000 0.000000U( 7) 34.00000 0.000000U( 8) 21.00000 0.000000U( 9) 23.00000 0.000000U( 10) 23.00000 0.000000U( 11) 7.000000 0.000000U( 12) 1.000000 0.000000U( 14) 2.000000 0.000000U( 15) 2.000000 0.000000U( 17) 1.000000 0.000000
将剩余的长度的带入,得出成品一的分配方案有1213327种,相比于带入无处理成品二后数据的直接计算的分配方案量级没变。
但如果不算降级处理的东西分配方案仅有59942种
单独解决成品一:
Global optimal solution found.Objective value: 14.00000Objective bound: 14.00000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 8821Variable Value Reduced CostU( 2) 5.000000 0.000000U( 4) 6.000000 0.000000U( 5) 1.000000 0.000000U( 6) 3.000000 0.000000U( 9) 23.00000 0.000000U( 10) 23.00000 0.000000U( 11) 7.000000 0.000000U( 12) 1.000000 0.000000U( 14) 2.000000 0.000000U( 15) 2.000000 0.000000U( 17) 1.000000 0.000000
局部最优解
成品三137个,成品二37个,成品三14个,总188个
相关文章:

【数学建模】天然肠衣搭配问题
2011高教社杯全国大学生数学建模竞赛D题 天然肠衣(以下简称肠衣)制作加工是我国的一个传统产业,出口量占世界首位。肠衣经过清洗整理后被分割成长度不等的小段(原料),进入组装工序。传统的生产方式依靠人工…...
Dockerfile实践java项目
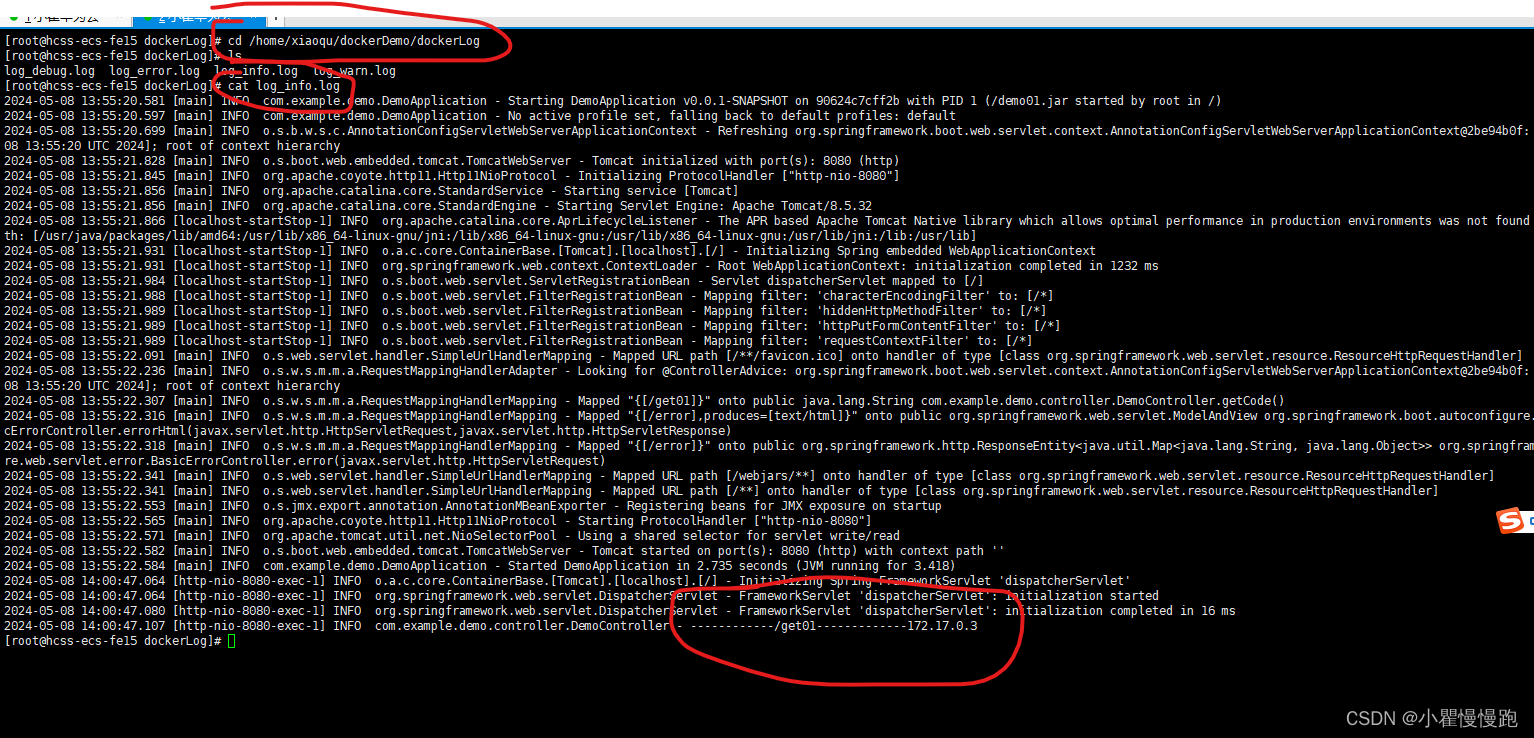
目的:用java项目测试dockerfil部署(前提是安装好了docker) 部署准备文件如下 1. java项目 java项目demo地址 https://gitee.com/xiaoqu_12/dockerfileDemo.git 或者百度网盘直接下载打包好的jar包 链接:https://pan.baidu.com/s/…...

【管理咨询宝藏96】企业数字化转型的中台战略培训方案
本报告首发于公号“管理咨询宝藏”,如需阅读完整版报告内容,请查阅公号“管理咨询宝藏”。 【管理咨询宝藏96】企业数字化转型的中台战略培训方案 【格式】PDF版本 【关键词】SRM采购、制造型企业转型、数字化转型 【核心观点】 - 数字化转型是指&…...

【webrtc】MessageHandler 3: 基于线程的消息处理:以sctp测试为例
消息处理可以用于模拟发包处理G:\CDN\rtcCli\m98\src\net\dcsctp\socket\dcsctp_socket_network_test.cc 这个实现中,onMessage还是仅对了一种消息进行处理,就是接收则模式下,打印带宽。当然,可能程序有多个消息,分别在不同的onmessage中执行?SctpActor:以一个恒定的速率…...

redisson 使用脚本实现将一个队列的元素弹出并推入另一个队列的原子操作
脚本逻辑: 从队列1弹出元素如果存在值则推入队列2否则返回null RScript script redissonClient.getScript(); final String scriptText """local value redis.call(lpop, KEYS[1]);if value thenredis.call(rpush, KEYS[2], value);return valu…...

基于Springboot的校园新闻管理系统(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的校园新闻管理系统(有报告)。Javaee项目,springboot项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构…...

Windows环境下基于CMake构建Lua
Windows环境下基于CMake构建Lua 环境!!!注意: lua-5.4.6.tar.gz压缩包中,并未提供luac.c文件,无法构建luac.exe,可以从lua-5.4.5.tar.gz压缩包中拷贝使用 一、搭建基于CMake构建的Lua环境二、构…...
LLM⊗KG范式下的知识图谱问答实现框架思想阅读
分享一张有趣的图,意思是在分类场景下,使用大模型和fasttext的效果,评论也很逗。 这其实背后的逻辑是,在类别众多的分类场景下,尤其是在标注数据量不缺的情况下,大模型的收益是否能够比有监督模型的收益更多…...

ue引擎游戏开发笔记(35)——为射击添加轨道,并显示落点
1.需求分析: 我们只添加了开枪特效,事实上并没有实际的效果产生例如弹痕,落点等等。所以逐步实现射击的完整化,先从实现落点开始。 2.操作实现: 1.思路:可以这样理解,每次射击的过程是一次由摄…...

路由策略与路由控制
1.路由控制工具 匹配工具1:访问控制列表 (1)通配符 当进行IP地址匹配的时候,后面会跟着32位掩码位,这32位称为通配符。 通配符,也是点分十进制格式,换算成二进制后,“0”表示“匹配…...

JAVA版本的ATM编程问题记录
前段时间用C语言写了个银行ATM系统,还写了一篇文章记录了一些,C语言的ATM文章。后来又用IDEA写了一个JAVA版本的银行ATM。有人就会问为啥浪费这个时间写ATM呢?🧐其实是我本科代码没学好,所以现在想利用比较熟悉的ATM系…...
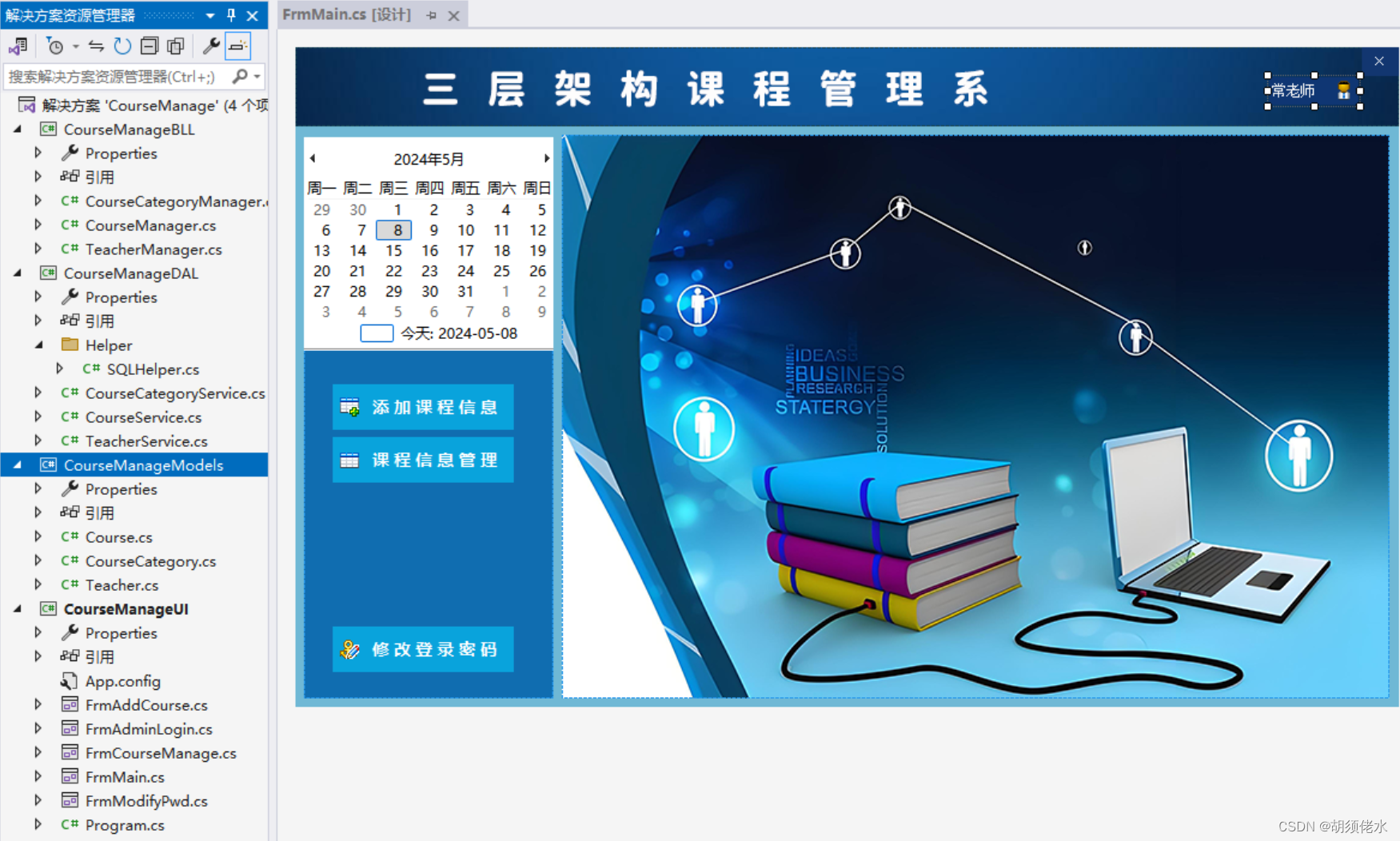
C#winfrom三层架构实现简单课程管理系统管理系统,三层架构实现增删改查
1. 项目展示 1.1登录展示 1.2添加课程信息展示 1.3课程信息管理-查询-修改-删除 1.4修改登录密码 2.项目功能介绍(图) 3.数据库设计 3.1 教师表设计 3.2 课程分类表 3.3 课程信息表 4. 创建样式界面 winfrom 超详细UI创建过程 实现双色球选号器UI界面…...
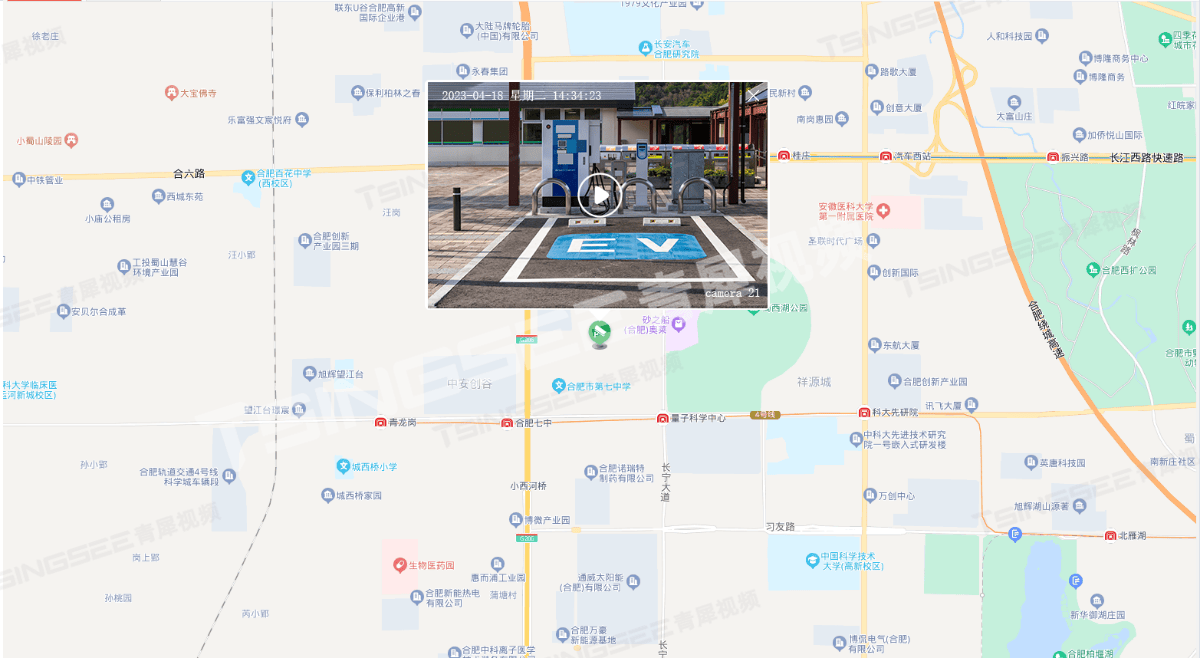
AI技术赋能下的视频监控方案是如何解决新能源汽车充电难问题的?
一、方案背景 刚刚结束的第十八届北京车展异常火爆,其中一组与汽车有关的数字让人格外关注。根据乘联会2024年4月19日公布的最新数据,全国乘用车市场零售达到51.6万辆,其中新能源车的销量约为26万辆,市场渗透率达到50.39%。 这意味…...

长难句打卡5.6
For H&M to offer a $5.95 knit miniskirt in all its 2,300-plus stores around the world, it must rely on low-wage overseas labor, order in volumes that strain natural resources, and use massive amounts of harmful chemicals. 翻译:H&M若要在其全球总共2…...
总结)
PDF编辑器软件常见问题(技巧)总结
目录 问题pdf高级编辑器中编辑文字时" 格式 " 如何出现? 待续、更新中 问题 pdf高级编辑器中编辑文字时" 格式 " 如何出现? shiftF4 待续、更新中 1 顿号“、” : 先使用ctrl. 再使用一遍切回 2 下标: 在数字两边加上 ~ 即可 , 21 3 上标: 2 0 2^{0} …...
)
Dive into Deep Learning-优化算法(1)
优化和深度学习的关系 优化是最小化损失函数,而深度学习的目标是在给定有限数据量的情况下寻找合适的模型,分别对应着训练误差和泛化误差;需要注意过拟合; 优化面临的挑战(求解数值解) 局部最小值&#…...
Partisia Blockchain 生态首个zk跨链DEX现已上线
在5月1日,由Partisia Blockchain与zkCross创建合作推出的Partisia zkCrossDEX在Partisia Blockchain生态正式上线。Partisia zkCrossDEX是Partisia Blockchain上重要的互操作枢纽,其融合了zkCross的zk技术跨链互操作方案,并利用Partisia Bloc…...
.NET操作 Access (MSAccess)
注意:新项目推荐 Sqlite ,Access需要注意的东西太多了,比如OFFICE版本,是X86还是X64 连接字符串 ProviderMicrosoft.ACE.OleDB.15.0;Data Source"GetCurrentProjectPath"\\test.accdb//不同的office版本 连接字符串有…...

shell脚本,删除30天以前的日志,并将日志推送到nas,但运行出现/bin/bash^M。
删除30天以前的日志 将日志推送到nas中,然后删除pod中的日志 pod挂载到本地 运行出现/bin/bash^M 1、删除30天以前的日志: #! /bin/bash# 定义源日志目录 LOG_DIR/home/log/ # 删除日志 find $LOG_DIR -type f -name "*.log" -mtime 30 -exec…...

现身说法暑期三下乡社会实践团一个好的投稿方法胜似千军万马
作为一名在校大学生,去年夏天我有幸参与了学院组织的暑期大学生三下乡社会实践活动,这段经历不仅让我深入基层,体验了不一样的生活,更是在新闻投稿的实践中,经历了一次从传统到智能的跨越。回忆起那段时光,从最初的邮箱投稿困境,到后来智慧软文发布系统的高效运用,每一步都刻印…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
