codeforce#938 (div3) 题解
C. Inhabitant of the Deep Sea
数组第一个元素减一下,最后一个元素减一下,一共能减k次,问有多少元素能减到0.细节模拟我是傻逼,有问题建议直接看tc面像tc编程
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 2e5+5;int n;
ll k;
ll store[maxn];
int main() {IOSint t;cin>>t;while(t--) {cin>>n>>k;rep(i,0,n) cin>>store[i];ll m_right = k/2LL;ll m_left = m_right + k % 2LL;int ans = 0;int inf = 0, sup = n-1;while((m_right>0 || m_left>0) && inf<=sup) {if (inf == sup) {if (m_right + m_left >= store[inf]) {ans ++;}break;}if (m_left >= store[inf]) {ans ++;m_left -= store[inf];inf ++;} else {store[inf] -= m_left;m_left = 0;}if (m_right >= store[sup]) {ans ++;m_right -= store[sup];sup --;} else {store[sup] -= m_right;m_right = 0;}}cout<<ans<<endl;}return 0;
}
D. Inaccurate Subsequence Search
给数组a和数组b,问a中有多少子数组在重排后有至少k个元素相同。
滑动窗口。首先遍历b得出有多少种字母以及每个字母有多少。然后滑动窗口维护窗口内字母的个数,窗口前进时pop首位push末尾,update维护信息,然后每次窗口移动进行对比是否符合条件
finish
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 2e5+5;const int sub_maxn = 1e6+5;int n,k,m;
int store[maxn], partten[maxn];
map<int,bool> matches;
map<int, int> used, have;
int main() {IOSint t;cin>>t;while(t--) {cin>>n>>m>>k;rep(i,0,n) cin>>store[i];rep(i,0,m) cin>>partten[i];matches.clear();used.clear();rep(i,0,m)if (matches[partten[i]]) {have[partten[i]] ++;} else {matches[partten[i]] = true;have[partten[i]] = 1;}int pos = 0,match_num = 0;int ans = 0;while(pos<n) {int num = store[pos];if (pos < m) {if (matches[num]) {if(used[num] < have[num]) match_num ++;used[num] ++;}} else {
// cout<<"pos:"<<pos<<" match:"<<match_num<<endl;if (match_num >= k) {ans ++;}// popint pop_pos = pos - m;int pop_num = store[pop_pos];if (matches[pop_num]){used[pop_num] --;if (used[pop_num] < have[pop_num]) match_num --;}// pushif (matches[num]) {if(used[num] < have[num]) match_num ++;used[num] ++;}}pos ++;}if (match_num >= k) ans ++;cout<<ans<<endl;}return 0;
}
E. Long Inversions
给出一个二进制序列s,每次可以选择长度为k的连续子列取反,问能让s的每一位都变成1的最大k是多少
枚举暴力k值,倒序遍历n,发现可以直接输出。毕竟 n 2 n^2 n2也不大。
然后再说下怎么验证可以让s全变1.当我们在s中发现一个0,那么肯定是要反转一次的,然后继续下一位,这样全部遍历一遍看还有没有0,没有就是可以
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 5e3+5;string store;
bool check(int);
int main() {IOSint t;cin>>t;while(t--) {int n;cin>>n;cin>>store;int inf = n;drep(inf,n,0) {if(check(inf)) {cout<<inf<<endl;break;}}}return 0;
}
bool check(int k) {int pos = 0;int len = store.length();vector<int> cnt(len+1,0);int inv_cnt = 0;bool res = true;while(pos<len) {inv_cnt += cnt[pos];int num = store[pos] - '0';if (inv_cnt%2)num = num ^ 1;if (!num) {if (pos+k<=len) {inv_cnt ++;cnt[pos+k] = -1;} else {res = false;break;}}pos ++;}return res;
F. Unfair Game
给一堆1234,如果这些数XOR结果是0会赢,现在每次拿走一个,问最多能赢几次。
显然4和123不属于一类,单纯考虑4,那么就赢4的个数/2次。然后我们来看123.
记dp[i][j][k]为1个数为i个,2个数为j,3个数为k时赢的次数。初始dp[0][0][0]为0。当且仅当i个1,j个2,k个3XOR时dp[i][j][k] + 1(由于XOR性质,这里只需要判断奇偶再运算就可以),转移方程
d p [ i ] [ j ] [ k ] = m a x ( d p [ i − 1 ] [ j ] [ k ] , d p [ i ] [ j − 1 ] [ k ] , d p [ i ] [ j ] [ k − 1 ] dp[i][j][k] = max(dp[i-1][j][k], dp[i][j-1][k], dp[i][j][k-1] dp[i][j][k]=max(dp[i−1][j][k],dp[i][j−1][k],dp[i][j][k−1]
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;int p[5];
int dp[205][205][205];
void pre();
int main() {IOSpre();int t;cin>>t;while(t--) {rep(i,0,4) cin>>p[i];int ans = p[3] / 2 + dp[p[0]][p[1]][p[2]];cout<<ans<<endl;}return 0;
}
void pre() {int lim = 201;dp[0][0][0] = -1;rep(i,0,lim) {rep(j,0,lim) {rep(k,0,lim) {if (i) dp[i][j][k] = max(dp[i][j][k], dp[i-1][j][k]);if (j) dp[i][j][k] = max(dp[i][j][k], dp[i][j-1][k]);if (k) dp[i][j][k] = max(dp[i][j][k], dp[i][j][k-1]);int ans = ((i&1) * 1 ) ^ ((j&1) * 2) ^ ((k&1) * 3);if (!ans)dp[i][j][k] ++;}}}
}
G. GCD on a grid
求从(1,1)到(n,m)的最大公约数。
这个题其实也是枚举,但是根据题意,答案一定是(1,1)和(n,m)公约数的因数。
然后我们拿着因数num对整个矩阵求余,看有没有一条路径从(1,1)到(n,m)上所有的元素都是num的倍数,如果有,那么就是候选答案,遍历所有因数后从候选答案选最大。
至于路径的查询用的dp。记dp[i][j]为(i,j)是否是因数num的倍数。当且仅当 s t o r e [ i ] [ j ] m o d n u m store[i][j] \mod num store[i][j]modnum为true,转移方程
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] ∥ d p [ i ] [ j − 1 ] dp[i][j] = dp[i-1][j] \parallel dp[i][j-1] dp[i][j]=dp[i−1][j]∥dp[i][j−1]
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <time.h>
#include <set>
#include <map>
#include <queue>#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define mem(A,B) memset(A,B,sizeof(A));
#define rep(index,start,end) for(int index = start;index < end; index ++)
#define drep(index,start,end) for(int index = start;index >= end; index --)using namespace std;typedef long long ll;const int maxn = 128;ll gcd(ll,ll);int n,m;
int store[maxn][maxn];
bool dp[maxn][maxn];
void init();
void show();
bool check(int);
int main() {IOSint t;cin>>t;while(t--) {cin>>n>>m;rep(i,0,n) rep(j,0,m)cin>>store[i][j];int ans = 1;int num = gcd(store[0][0], store[n-1][m-1]);int lim = sqrt(num);for(int i=1;i*i<=num;i++) {if (num % i) continue;if (check(i)) {ans = max(ans, i);}if (check(num/i))ans = max(ans, num/i);}cout<<ans<<endl;}return 0;
}
ll gcd(ll a, ll b){ll t;while(b){t = b;b = a % b;a = t;}return a;
}
void init() {rep(i,0,n) rep(j,0,m) dp[i][j] = false;
}
void show() {rep(i,0,n) {rep(j,0,m) cout<<dp[i][j]<<' ';cout<<endl;}
}
bool check(int num) {if (num == 1) return true;rep(i,0,n) {rep(j,0,m) {dp[i][j] = (store[i][j] % num) == 0;bool tmp = false;if (i && dp[i-1][j]) tmp = tmp || dp[i-1][j];if (j && dp[i][j-1]) tmp = tmp || dp[i][j-1];if (i || j) dp[i][j] = dp[i][j] && tmp;}}return dp[n-1][m-1];
}
相关文章:
 题解)
codeforce#938 (div3) 题解
C. Inhabitant of the Deep Sea 数组第一个元素减一下,最后一个元素减一下,一共能减k次,问有多少元素能减到0.细节模拟我是傻逼,有问题建议直接看tc面像tc编程 #include <iostream> #include <string.h> #include &…...
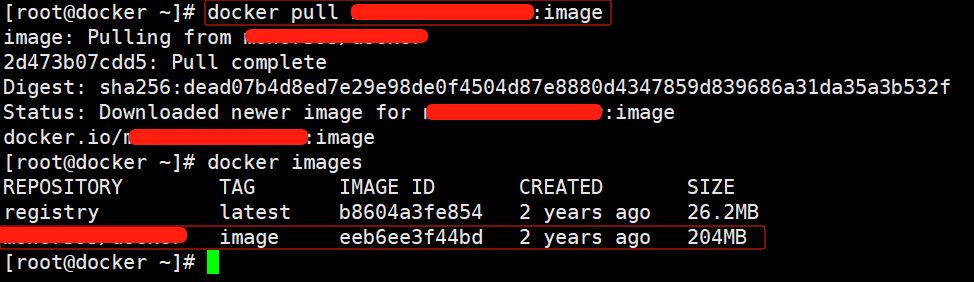
【Docker】如何注册Hub账号并上传镜像到Hub仓库
一、创建Hub账户 浏览器访问:hub.docker.com 点击【Sign up】注册账号 输入【邮箱】【用户名】【密码】 ps:用户名要有字母数字;订阅不用勾选 点击【Sign up】注册即可 点击【Sign in】登录账号 输入【邮箱】【密码】 点击【Continue】登录 二…...
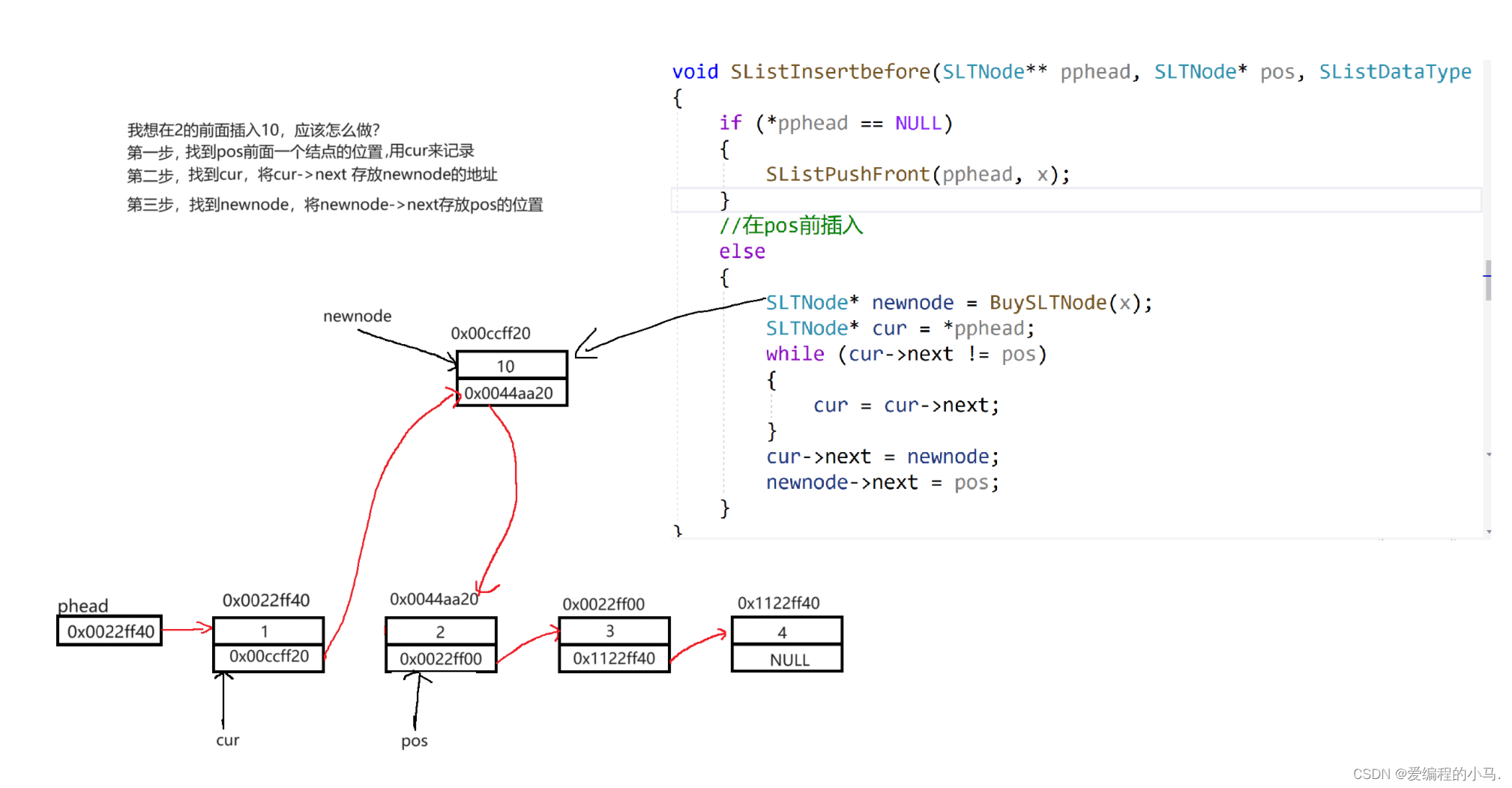
[初阶数据结构】单链表
前言 📚作者简介:爱编程的小马,正在学习C/C,Linux及MySQL。 📚本文收录于初阶数据结构系列,本专栏主要是针对时间、空间复杂度,顺序表和链表、栈和队列、二叉树以及各类排序算法,持…...

项目使用git开发流程
第一步 项目初期:领导负责的工作 01 创建仓库:在码云上面创建仓库地址,创建完成后点击初始化README:郝陶涛/vue-tea 02 领导在桌面上将代码克隆下来:将代码克隆下来之后,切换到代码内部,使用g…...

Day 28 MySQL的数据备份与恢复
数据备份及恢复 1.概述 所有备份数据都应放在非数据库本地,而且建议有多份副本 备份: 能够防止由于机械故障以及人为误操作带来的数据丢失,例如将数据库文件保存在了其它地方 冗余: 数据有多份冗余,但不等备份&…...
疑问篇)
PackageKit的使用(三)疑问篇
本篇主要是一些疑问归纳,不做具体的函数分析,但是会给出关键点,查看源码就会很清楚了 apt source PackageKit 1. org.freedesktop.PackageKit D-Bus 接口介绍 D-Bus API Reference: PackageKit Reference Manual c库的接口可以看源码。 2.…...

【Linux】17. 进程间通信 --- 管道
1. 什么是进程间通信(进程间通信的目的) 数据传输:一个进程需要将它的数据发送给另一个进程 资源共享:多个进程之间共享同样的资源。 通知事件:一个进程需要向另一个或一组进程发送消息,通知它(它们)发生了…...
有哪些有效的复习方法可以帮助备考软考?
软考目前仍然是一个以记忆为主、理解为辅的考试。学过软考的朋友可能会感到困惑,因为软考的知识在日常工作中有许多应用场景,需要理解的地方也很多。但为什么我说它是理解为辅呢?因为这些知识点只要记住了,都不难理解,…...

【MySQL | 第九篇】重新认识MySQL锁
文章目录 9.重新认识MySQL锁9.1MySQL锁概述9.2锁分类9.2.1锁的粒度9.2.2锁的区间9.2.3锁的性能9.2.4锁的级别 9.3拓展:意向锁9.3.1意向锁概述9.3.2意向锁分类9.3.3意向锁作用(1)意向锁的兼容互斥性(2)例子1(…...

含义:理财风险等级R1、R2、R3、R4、R5
理财风险等级R1、R2、R3代表什么,为什么R1不保本,R2可能亏损 不尔聊投资https://author.baidu.com/home?frombjh_article&app_id1704141696580953 我们购买理财产品的时候,首先都会看到相关产品的风险等级。风险等级约定俗成有5级&…...

ICode国际青少年编程竞赛- Python-2级训练场-列表入门
ICode国际青少年编程竞赛- Python-2级训练场-列表入门 1、 Dev.step(3)2、 Flyer.step(1) Dev.step(-2)3、 Flyer.step(1) Spaceship.step(7)4、 Flyer.step(5) Dev.turnRight() Dev.step(5) Dev.turnLeft() Dev.step(3) Dev.turnLeft() Dev.step(7) Dev.turnLeft() Dev.…...
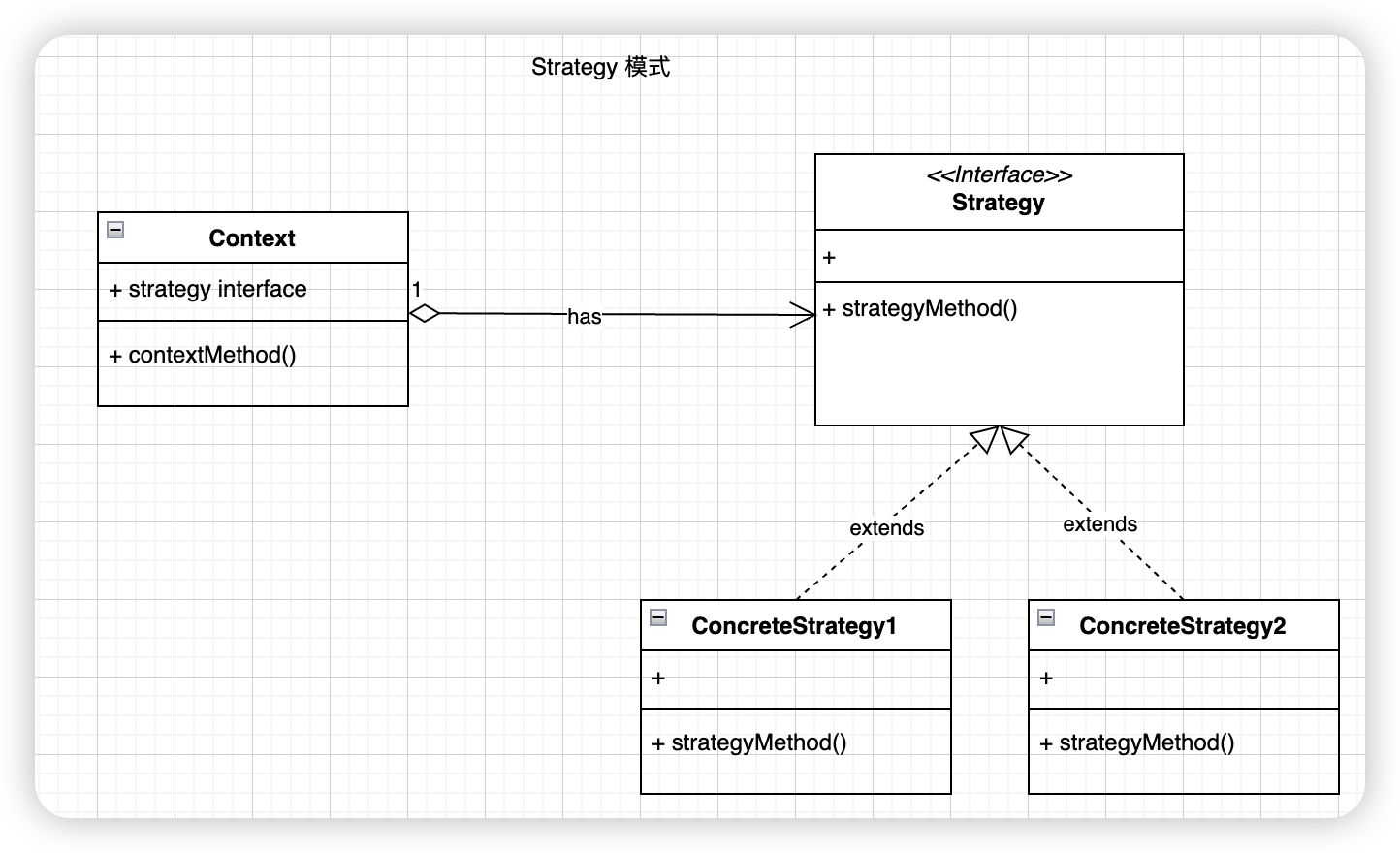
【设计模式】14、strategy 策略模式
文章目录 十四、strategy 策略模式14.1 map_app14.1.1 map_app_test.go14.1.2 map_app.go14.1.3 navigate_strategy.go 十四、strategy 策略模式 https://refactoringguru.cn/design-patterns/strategy 需求: client 知道很多不同的策略, 希望在运行时切换. 场景示例: 就像高…...
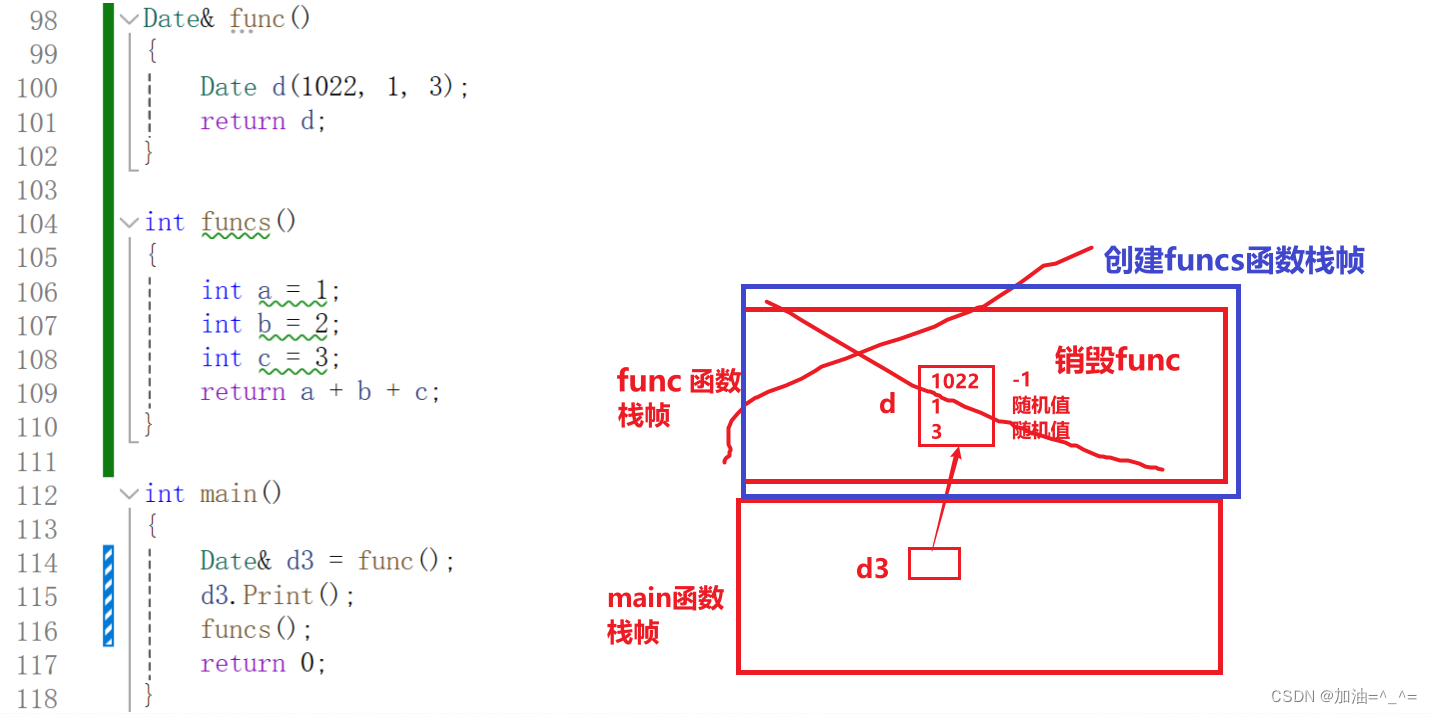
C++类和对象(基础篇)
前言: 其实任何东西,只要你想学,没人能挡得住你,而且其实学的也很快。那么本篇开始学习类和对象(C的,由于作者有Java基础,可能有些东西过得很快)。 struct在C中的含义: …...

Oracle导入数据中文乱码问题处理,修改客户端字符编码跟数据库的一致
前提:SQL文件打开其中中文字符是正常显示,保证导出文件中文字符正常。通过sqlplus命令导入SQL文件出现乱码,这是因为客户端跟数据库的字符集不一致导致出现乱码问题。 要SQL导入的中文正常,要确保执行导入命令的客户端字符编码跟…...
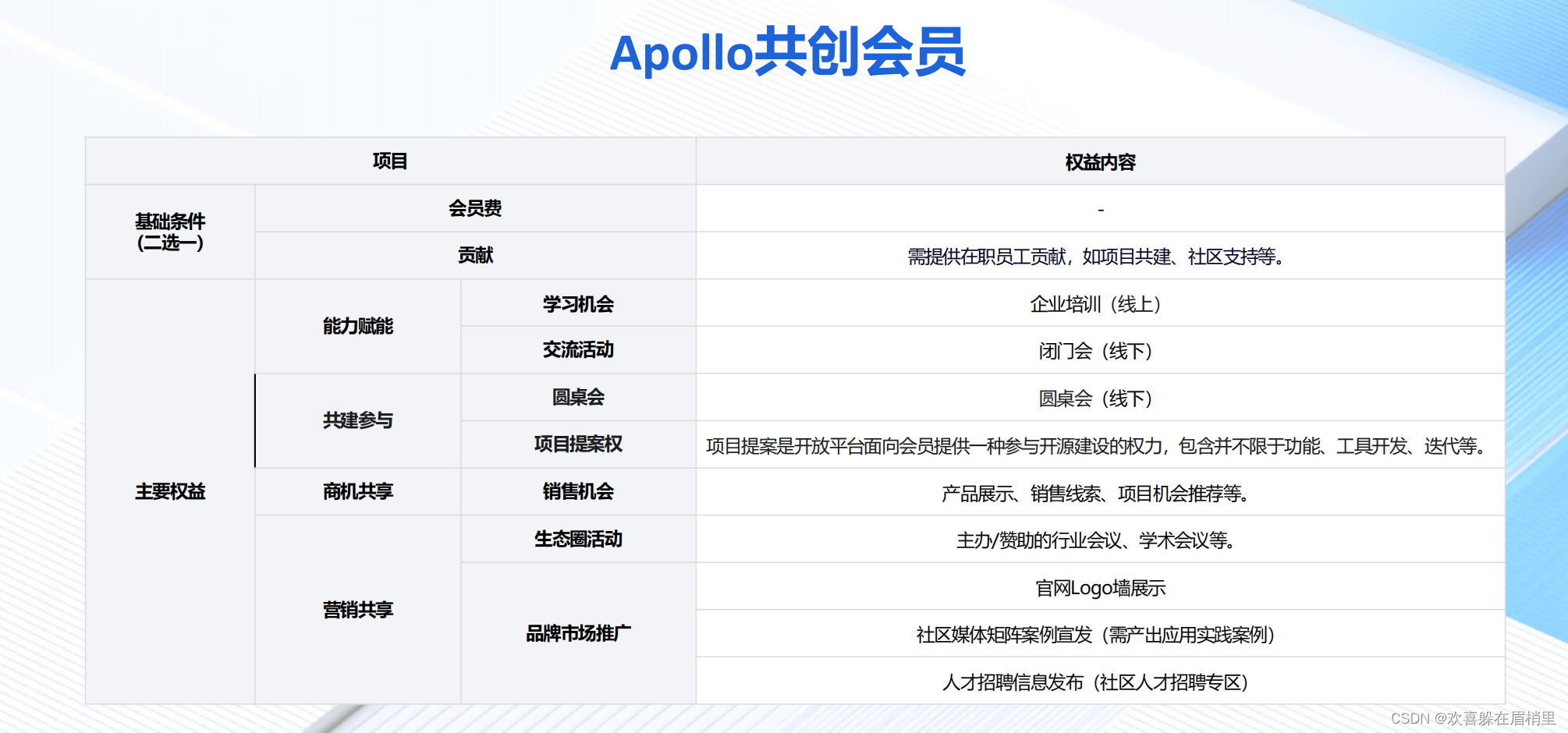
【与 Apollo 共创生态:展望自动驾驶全新未来】
1、引言 历经七年的不懈追求与创新,Apollo开放平台已陆续推出了13个版本,汇聚了来自全球170多个国家与地区的16万名开发者及220多家合作伙伴。随着Apollo开放平台的不断创新与发展,Apollo在2024年4月19日迎来了Apollo开放平台的七周年大会&a…...
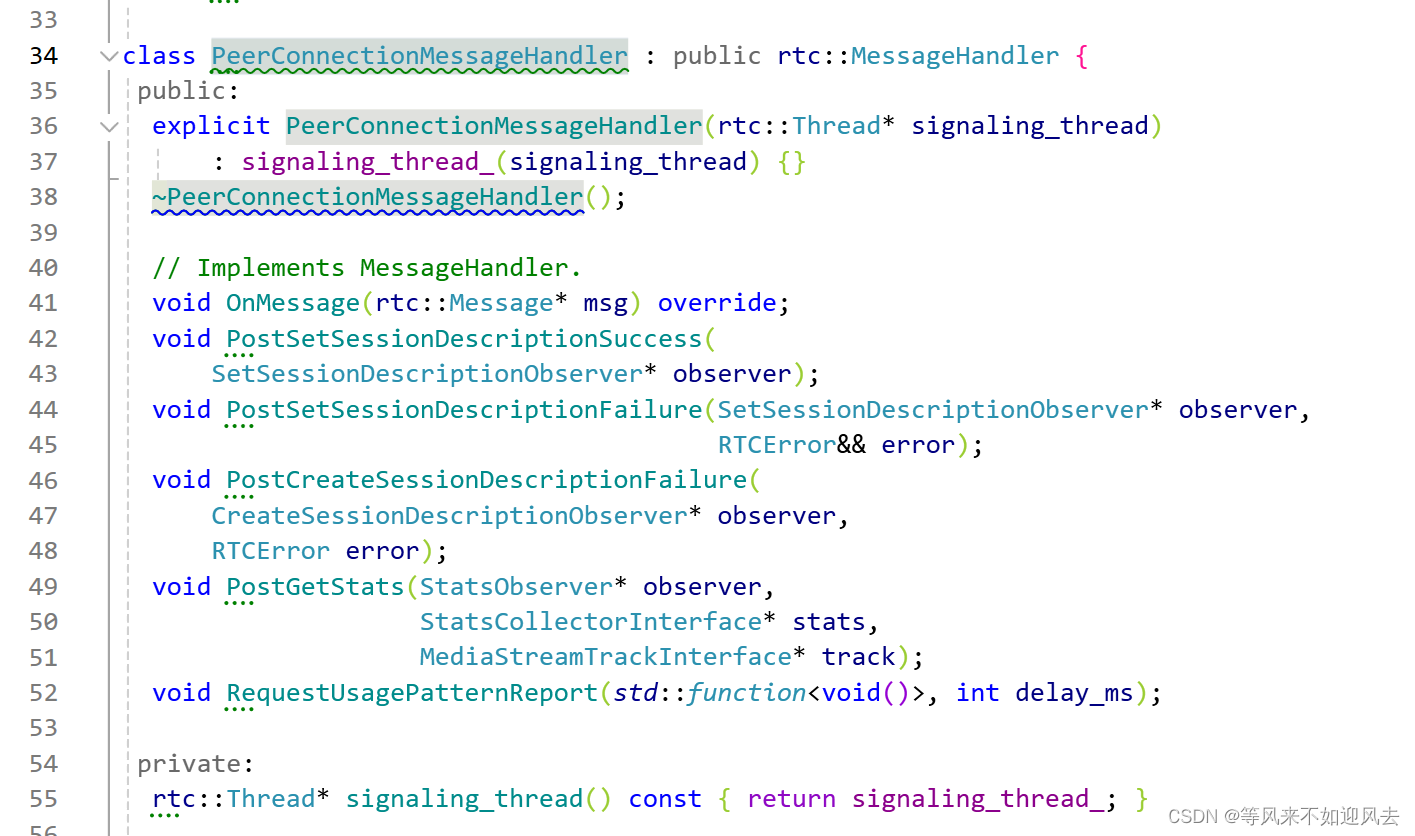
【webrtc】MessageHandler 5: 基于线程的消息处理:以PeerConnection信令线程为例
peerconn的信令是通过post 消息到自己的信令线程消息来处理的PeerConnectionMessageHandler 是具体的处理器G:\CDN\rtcCli\m98\src\pc\peer_connection_message_handler.hMachinery for handling messages posted to oneself PeerConnectionMessageHandler 明确服务于 signalin…...

计算机网络 3.2网络体系结构
第二节 网络体系结构 一、网络协议 1.定义: ①通信双方共同遵守的规则。 ②为网络数据交换制定的规则、约定与标准。 ③网络实体之间通信时有关信息传输顺序、信息格式、信息内容的约定或规则。 2.协议三要素: 语法:确定协议元素的格式…...
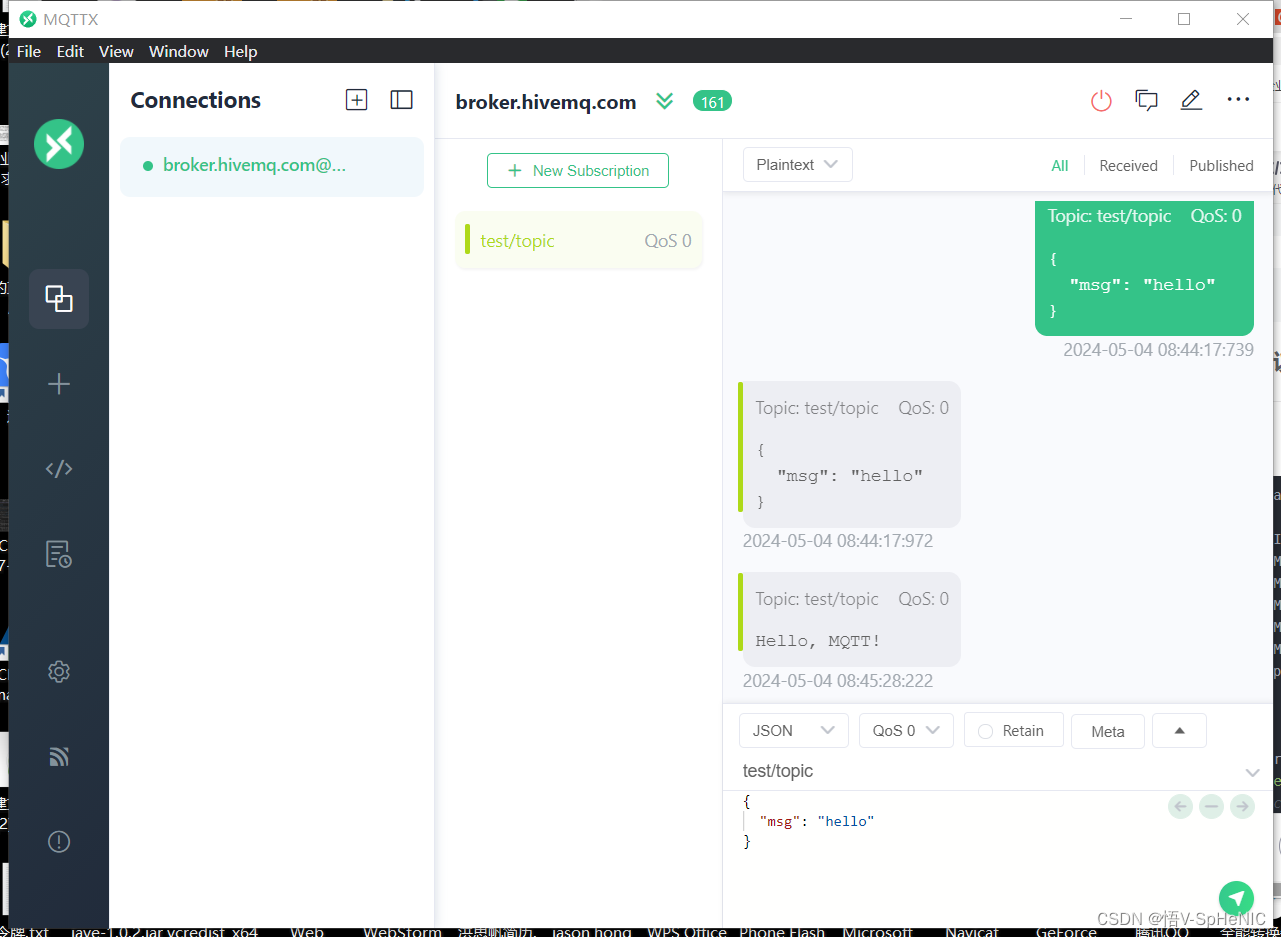
连接HiveMQ代理器实现MQTT协议传输
先下载MQTTX: MQTTX: Your All-in-one MQTT Client Toolbox 使用线上免费的MQTTX BROKER:The Free Global Public MQTT Broker | Try Now | EMQ 打开MQTTX,创建连接,点击NEW SUBSCRIPTION,创建一个主题,这里使用test/topic,在下面Json中填写…...
springcloud报错:Failed to start bean‘webServerStartStop‘
如果你正在使用nacos进行服务注册,然后报一下错误: 那就说明的nacos没有打开,所以找到你的下载nacos的文件夹 好了,错误完美解决~...

el-checkbox 无法动态设置勾选状态
问题 cheked 值动态变化,但是勾选状态无法动态改变 解决 v-model 与:checked 同时使用 <el-checkbox class"add-shop-check" v-model"renderData[0].isCheck" :checked"renderData[0].isCheck" change"checked > selec…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
