Rust:foo(x)、foo(x),还是foo(x.clone())?
一、一个实际问题
用一个线性代数库的求逆矩阵函数时,让我很不爽,我必须按照下面的形式写调用代码:
...if let Some(inv_mat) = try_inverse(mat.clone()) {...}...
注意 try_inverse 函数的参数传递形式,函数参数是 mat.clone() 而不是 mat,因为这个 mat 变量后面我还得使用。有看了几个其他的线性代数库,大都是按照这个形式定义的。我不得不思考一下为什么要这么干。
我们看这个函数的几种可能的声明形式:
fn try_inverse(mat: Mat) -> Option<Mat> {...} // .... (1)fn try_inverse(mat: &Mat) -> Option<Mat> {...} // .... (2)fn try_inverse(mat: &mut Mat) -> Option<Mat> {...} // .... (3)
下面分别讨论:
1、fn try_inverse(mat: Mat) -> Option
我们有两种办法向函数传递参数。如果 mat 函数调用后不再使用,可以直接把变量所有权转移给函数,按下面形式调用:
...if let Some(inv_mat) = try_inverse(mat) {...}...
如果 mat 在函数调用后还有别的用途,必须保留变量所有权,把变量克隆一份传递给函数,按照下面的方法调用:
...if let Some(inv_mat) = try_inverse(mat.clone()) {...}...
为什么么要这样传递参数?原因是,逆矩阵是在原矩阵的基础上构建出来了,这个构建过程会逐步覆盖掉原矩阵的数据。因此,求逆矩阵函数需要获得参数的所有权,在原矩阵基础上完成逆矩阵构建。
如果得不到所有权又如何?
2、fn try_inverse(mat: &Mat) -> Option
如果参数采用传递引用的方式,函数调用就变成了以下形式:
if let Some(inv_mat) = try_inverse(&mat) {...}
对我们来讲很是方便,但是这里存在一个效率问题。
无论 mat 我们后续是否使用,try_inverse() 都要首先克隆一个备份,然后在此基础上构建逆矩阵。也就是说,引用传参,形式上看调用方式很简洁,但是运行效率不高。而上面传值的方式,在参数后续不再使用时,可以省去变量完整克隆的运算时间。
那么,传递可修改引用可行吗?
3、fn try_inverse(mat: &mut Mat) -> Option
答案是不可以。我们看传入变量 &mut Mat 和返回结果 Option<Mat> 的语法形式就可以判断出,函数的结果和参数必须是两个独立的矩阵,不可能在参数的基础上构建逆矩阵。如果想利用传入的可变引用,函数声明需要改成下面的形式:
fn try_inverse(mat: &mut Mat) -> Option<&Mat> {...} // .... (4)
这又涉及到变量生命周期问题了。不难看出这个方式传入参数和返回结果,是一种导致语义复杂化、后患无穷的方法。
综上所述,函数声明(1)是一种最合适的形式,它把参数的克隆权交给了使用者,可避免不必要的克隆。声明(2) 虽然让使用者感觉很简洁,但牺牲了算法效率。声明(3)让参数变量冒着被修改的副作用,但没换来任何好处,所以不推荐。声明(4)的副作用问题多多,更不推荐。
二、函数传参技术要点
1、 foo(x):
foo(x) 的语法意义
- 如果foo函数的参数是按值接收(即它需要一个所有权的拷贝),那么你可以直接传递x。
- 这种方式下,x的所有权会被移动到foo函数中,之后你就不能再使用原始的x了,因为Rust的所有权规则不允许一个值有多个所有者。
foo(x) 的参数潜在的问题
- 开发应用程序时,参数
x大部分是胖指针类型的。如果我们希望函数foo调用后,传入的参数在函数执行后还能继续使用,这种参数定义模式下,我们必须按照下面的形式调用:
...foo(x.clone());...
也就是说,需要把变量的一个完整克隆移动到函数的参数栈,这样才不会影响变量 x 在函数调用后的可用性。但是,变量的完全克隆操作的代价通常很高。
2、 foo(&x):
- 如果
foo函数接收一个引用作为参数(例如fn foo(x: &T)),则你应该传递x的引用(&x)。 - 在这种情况下,
foo函数将获得x的借用,而不是所有权。这意味着你可以在调用foo之后继续使用x。 - 需要注意的是,根据Rust的借用规则,你不能在借用期间修改
x(除非foo接收一个可变引用,即fn foo(x: &mut T),并且你确实需要修改x)。
3、foo(x.clone()):
- 如果
foo函数需要一个值的拷贝,但你希望在调用之后仍然保留对原始x的使用权,你可以克隆x并传递克隆的版本。 - 这意味着你将创建一个
x的完整拷贝,并将其传递给foo函数,同时保留原始x的所有权和使用权。 - 使用
clone()可能会有性能开销,特别是当x很大时,因为它涉及到内存的分配和数据的复制。
在选择使用哪种方式时,你应该考虑以下因素:
- 函数的参数类型和要求。
- 你是否需要在调用函数之后继续使用
x。 x的大小和复制成本。- 是否有必要避免潜在的副作用或修改。
总的来说,在Rust中,这三种方式的选择受到语言所有权和借用规则的深刻影响,你需要根据具体情况来决定使用哪一种。
相关文章:
、foo(x),还是foo(x.clone())?)
Rust:foo(x)、foo(x),还是foo(x.clone())?
一、一个实际问题 用一个线性代数库的求逆矩阵函数时,让我很不爽,我必须按照下面的形式写调用代码: ...if let Some(inv_mat) try_inverse(mat.clone()) {...}...注意 try_inverse 函数的参数传递形式,函数参数是 mat.clone() 而…...
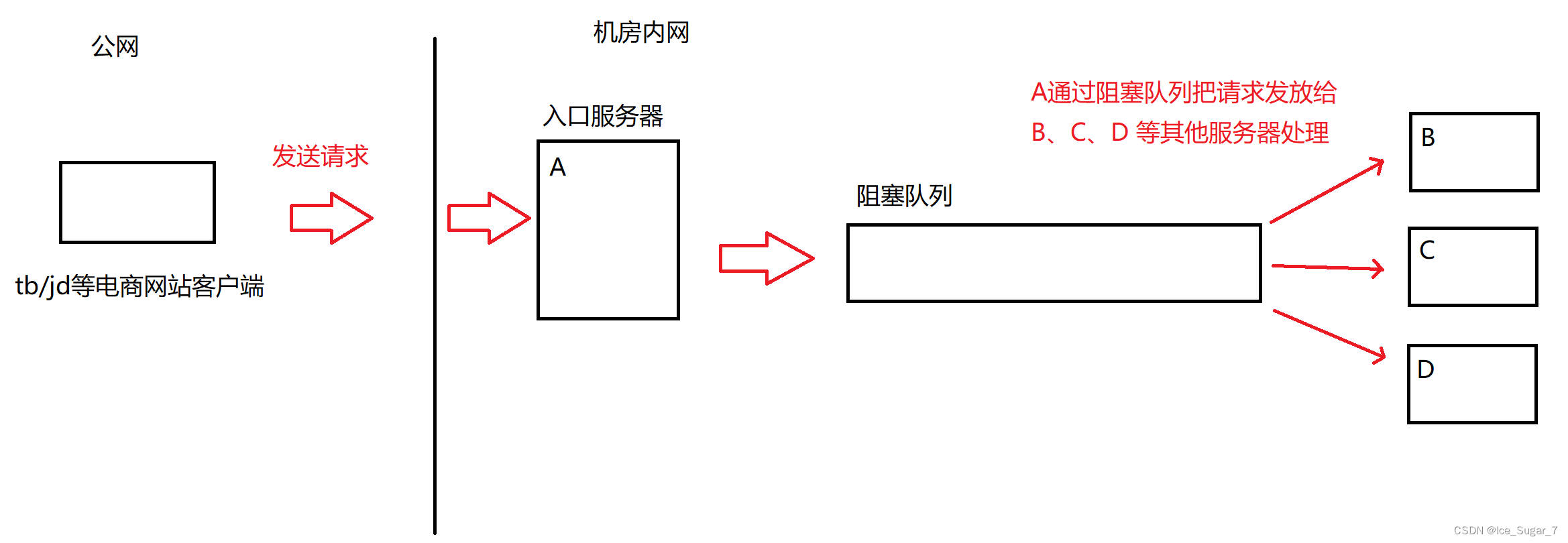
「JavaEE」多线程案例1:单例模式阻塞队列
🎇个人主页:Ice_Sugar_7 🎇所属专栏:JavaEE 🎇欢迎点赞收藏加关注哦! 多线程案例分析 🍉单例模式🍌饿汉模式🍌懒汉模式🍌指令重排序 🍉阻塞队列&a…...
pdf2htmlEX:pdf 转 html,医学指南精细化处理第一步
pdf2htmlEX:pdf 转 html,医学指南精细化处理第一步 单文件转换多文件转换 代码:https://github.com/coolwanglu/pdf2htmlEX 拉取pdf2htmlEX 的 Docker: docker pull bwits/pdf2htmlex # 拉取 bwits/pdf2htmlex不用进入容器&…...

【webrtc】MessageHandler 6: 基于线程的消息处理:StunRequest实现包发送和超时重传
G:\CDN\rtcCli\m98\src\p2p\base\stun_request.cc使用OnMessage 实现包的发送和包的超时重传StunRequest 一个StunRequest 代表是一个独立的请求的发送STUN消息 要不是发送前构造好的,要不就是按照需要构建的使用StunRequestManager: 每一个STUNRequest 携带一个交互id 写入m…...
《Python编程从入门到实践》day22
# 昨日知识点回顾 方法重构、驾驶飞船左右移动、全屏显示 飞船不移动解决,问题出在移动变量x更新 # Ship.pysnipdef update(self):"""根据移动标志调整飞船的位置"""# 更新飞船而不是rect对象的x值# 如果飞船右移的标志和飞船外接…...

介绍 ffmpeg.dll 文件以及ffmpeg.dll丢失怎么办的五种修复方法
ffmpeg.dll 是一个动态链接库文件,属于 FFmpeg运行库。它在计算机上扮演着非常重要的角色,因为它提供了许多应用程序和操作系统所需的功能和组件。当 ffmpeg.dll 文件丢失或损坏时,可能会导致程序无法正常运行,甚至系统崩溃。下面…...

AI换脸原理(6)——人脸分割介绍
一、介绍 人脸分割是计算机视觉和图像处理领域的一项重要任务,它主要涉及到将图像中的人脸区域从背景或其他非人脸区域中分离出来。这一技术具有广泛的应用场景,如人脸识别、图像编辑、虚拟背景替换等。 在计算机视觉(CV)领域,经典的分割技术可以主要划分为三类:语义分…...
线程的创建、分离和连接)
【C++并发编程】(二)线程的创建、分离和连接
文章目录 (二)线程的创建、分离和链接创建线程:示例线程的分离(detach)和连接(join) (二)线程的创建、分离和链接 创建线程:示例 线程(Thread&a…...

利用生成式AI重新构想ITSM的未来
对注入 AI 的生成式 ITSM 的需求,在 2023 年 Gartner AI 炒作周期中,生成式 AI 达到预期值达到顶峰后,三分之二的企业已经将生成式 AI 集成到其流程中。 你问为什么这种追求?在预定义算法的驱动下,IT 服务交付和管理中…...

完美解决AttributeError: module ‘backend_interagg‘ has no attribute ‘FigureCanvas‘
遇到这种错误通常是因为matplotlib的后端配置问题。在某些环境中,尤其是在某些特定的IDE或Jupyter Notebook环境中,可能会因为后端配置不正确而导致错误。错误信息提示 module backend_interagg has no attribute FigureCanvas 意味着当前matplotlib的后…...

CMakeLists.txt语法规则:条件判断中表达式说明一
一. 简介 前面学习了 CMakeLists.txt语法中的 部分常用命令,常量变量,双引号的使用。 前面一篇文章也简单了解了 CMakeLists.txt语法中的条件判断,文章如下: CMakeLists.txt语法规则:条件判断说明一-CSDN博客 本文…...
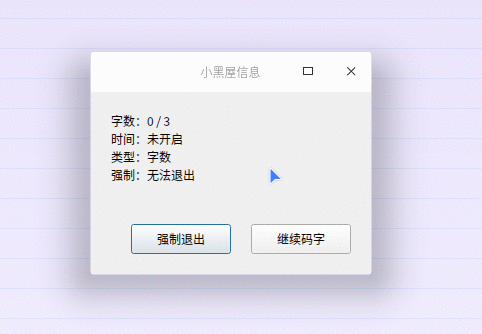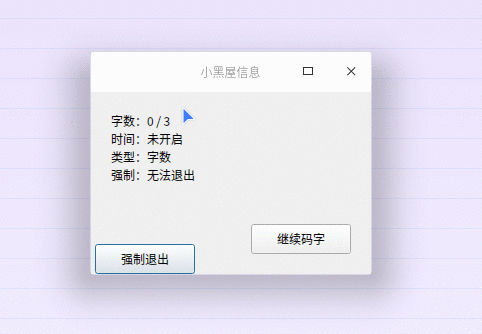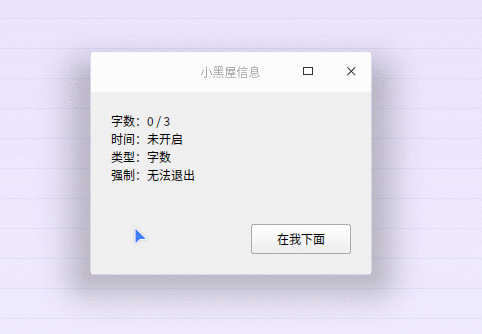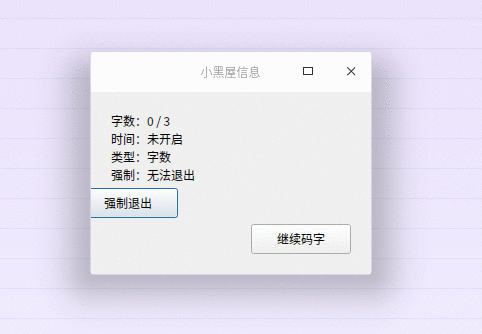
《QT实用小工具·五十三》会跑走的按钮
1、概述 源码放在文章末尾 该项目实现了会逃跑的按钮: 两个按钮,一个为普通按钮,另一个为会跑走的按钮 鼠标移到上面时,立刻跑掉 针对鼠标、键盘、触屏进行优化 随机交换两个按钮的文字、偶尔钻到另一个按钮下面、鼠标移开自…...

Servlet的几种用法?
serlet 1.定义:Serlet是使用Java编写的运行在服务器端的程序 2.Servlet主要是用于处理浏览器端发送的Http请求,并返回一个响应 3.Servlet开发需要使用到的包: java.servlet java.servlet.http 一.Servlet注册 1.xml方式 <servlet>…...

Golang | Leetcode Golang题解之第69题x的平方根
题目: 题解: func mySqrt(x int) int {if x 0 {return 0}C, x0 : float64(x), float64(x)for {xi : 0.5 * (x0 C/x0)if math.Abs(x0 - xi) < 1e-7 {break}x0 xi}return int(x0) }...

AR人脸美妆SDK解决方案,让妆容更加贴合个人风格
美妆行业正迎来前所未有的变革,为满足企业对高效、精准、创新的美妆技术需求,美摄科技倾力打造了一款企业级AR人脸美妆SDK解决方案,为企业打开美妆领域的新世界大门。 革命性的人脸美妆技术 美摄科技的AR人脸美妆SDK解决方案,不…...
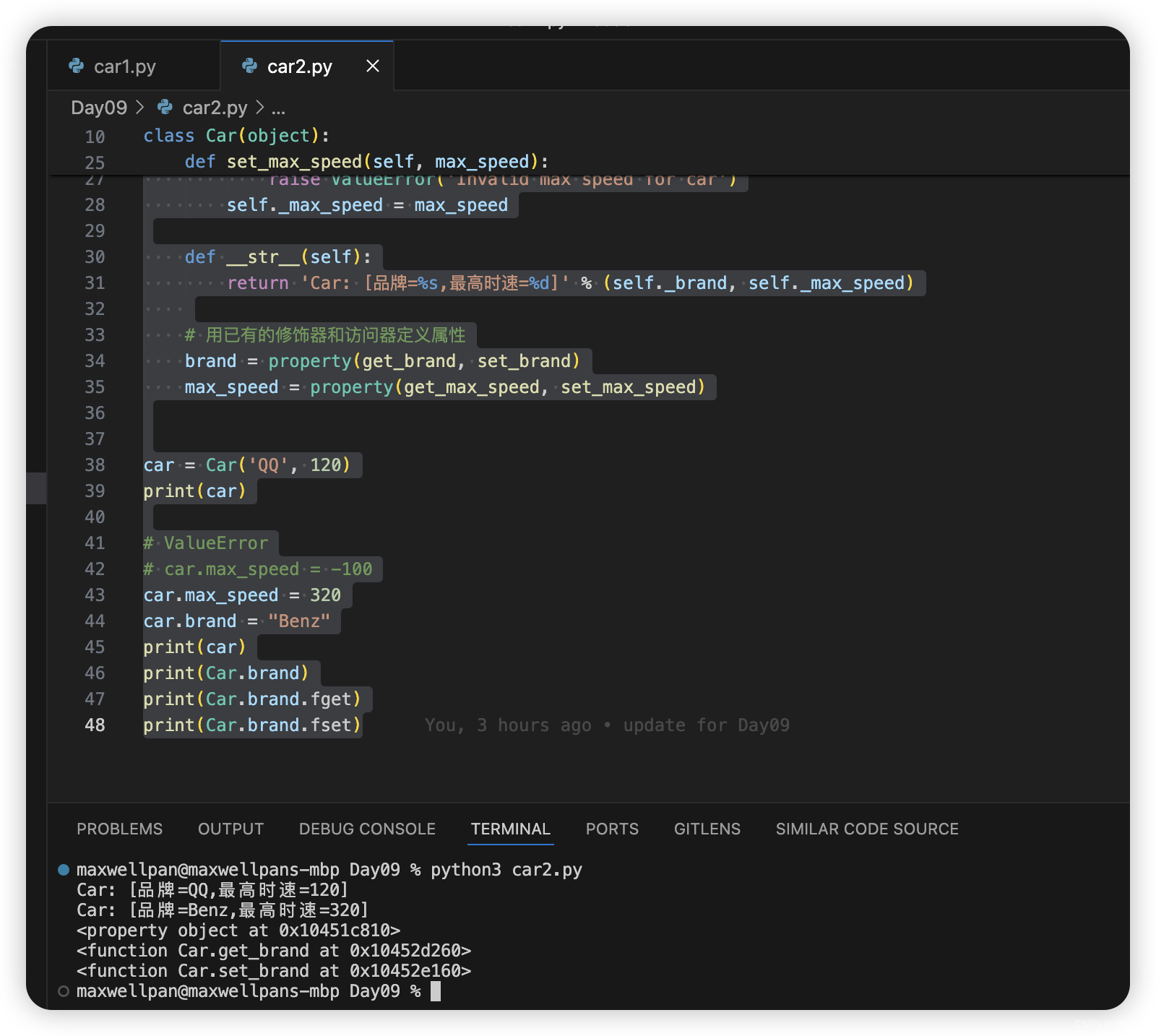
Python-100-Days: Day09 Object-oriented programming(OOP) Upgrade
1.property装饰器 之前有讨论过, Python中属性和方法访问权限的问题,不建议将属性设置为私有的,倘若直接将属性暴露给外界也是存在问题的。例如,我们没有办法检查赋给属性的值是否有效。之前的建议是将属性命名以单下划线开头&am…...
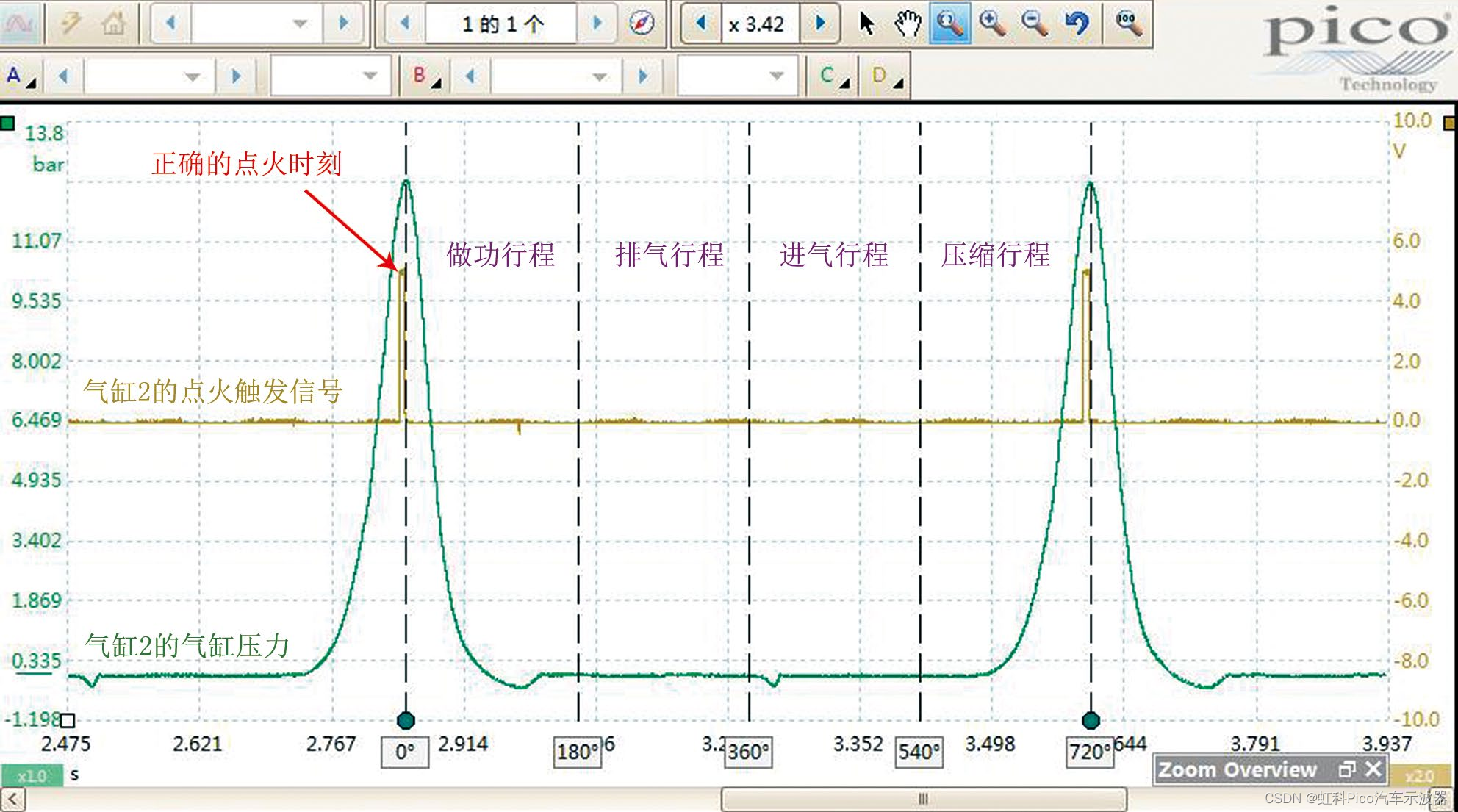
虹科Pico汽车示波器 | 免拆诊断案例 | 2010款凯迪拉克SRX车发动机无法起动
故障现象 一辆2010款凯迪拉克SRX车,搭载LF1发动机,累计行驶里程约为14.3万km。该车因正时链条断裂导致气门顶弯,大修发动机后试车,起动机运转有力,但发动机没有着机迹象;多起动几次,火花塞会变…...

ECC 号码总结
1、问题背景 在手机开发过程中,经常遇见各种紧急号码问题,在此特意总结下紧急号码相关知识。 2、紧急号码来源 在MTK RILD EccNumberSource.h中,定义了如下几种紧急号码来源。 按优先级排序介绍如下 2.1、SOURCE_NETWORK 网络下发ÿ…...
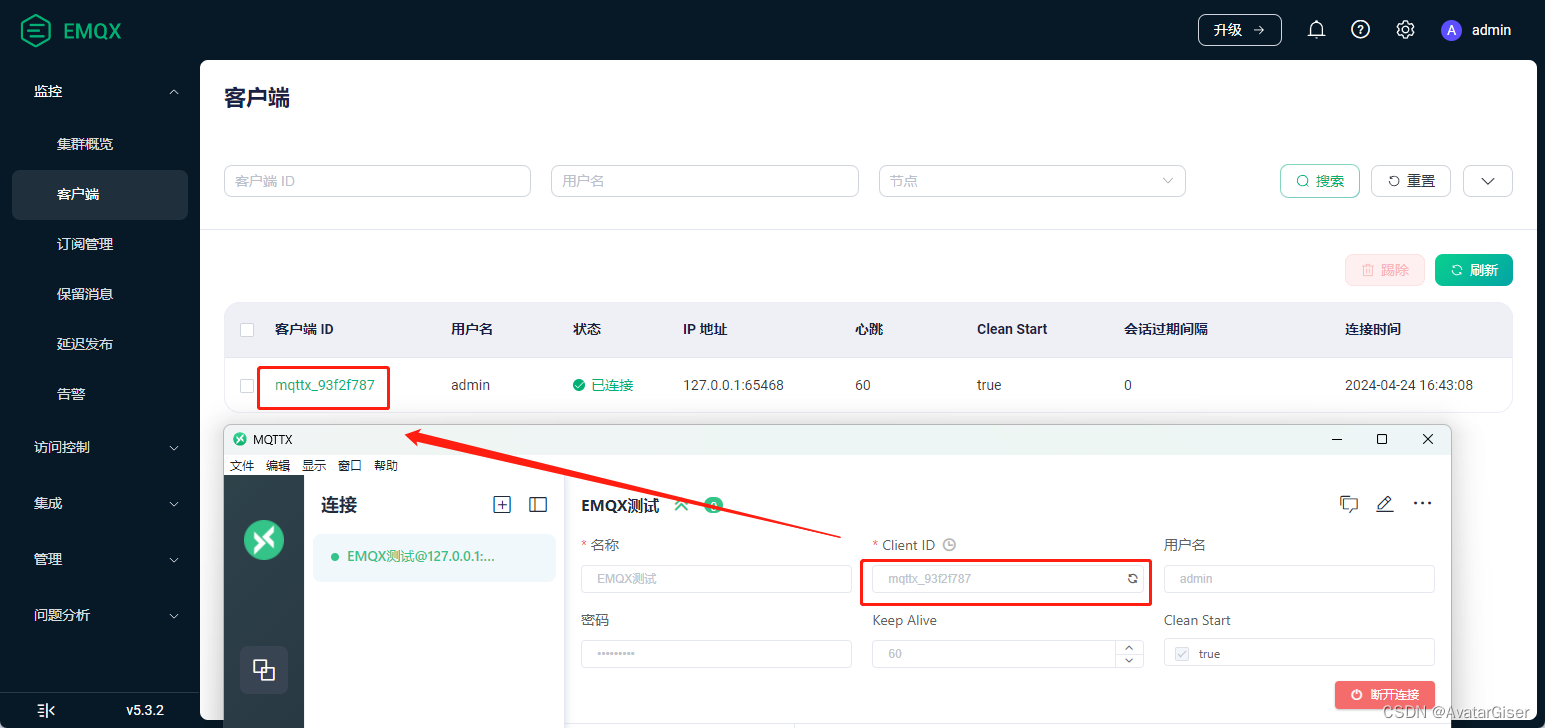
《大疆二次开发》EMQX和MQTT部署
EMQX 服务器 基础知识 概念 EMQX (Erlang/Enterprise/Elastic MQTT Broker) ;EMQ/EMQX就是MQTT Broker的一种实现;一款开源的大规模分布式 MQTT 消息服务器,功能丰富,专为物联网和实时通信应用而设计;支持多种协议&…...

【网络】滑动窗口和拥塞窗口
滑动窗口和拥塞窗口是TCP协议中两个重要的窗口概念,它们分别用于流量控制和拥塞控制,在功能和作用上有所不同。 滑动窗口(Sliding Window) 滑动窗口是用于流量控制的机制,它定义了发送方和接收方之间的数据传输量。T…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
