SwiGLU激活函数
SwiGLU激活函数已经成为LLM的标配了。它是GLU的变体,公式如下:
SwiGLU ( x , W , V , b , c , β ) = Swish β ( x W + b ) ⊗ ( x V + c ) \operatorname{SwiGLU}(x, W, V, b, c, \beta)=\operatorname{Swish}_\beta(x W+b) \otimes(x V+c) SwiGLU(x,W,V,b,c,β)=Swishβ(xW+b)⊗(xV+c)
Swish
S w i s h β ( x ) = x ⊗ σ ( β x ) \operatorname{Swish_\beta}(x)=x \otimes \sigma(\beta x) Swishβ(x)=x⊗σ(βx)
在nlp和cv任务上,Swish性能都和GELU接近,稍微略高点。但Swish公式更简洁优雅。
GELU早期被BERT、RoBERTa、ALBERT采用。
GLU
GLU ( x , W , V , b , c ) = σ ( x W + b ) ⊗ ( x V + c ) \operatorname{GLU}(x, W, V, b, c)=\sigma(x W+b) \otimes(x V+c) GLU(x,W,V,b,c)=σ(xW+b)⊗(xV+c)
单纯从公式看,GLU是一个神经网络层。左右两个线性变换层,左边再接一个门控机制来控制信息流通多少。
SwiGLU
将Swish作为左侧激活函数就得到了SwiGLU。代码如下:
F.silu(self.w1(x)) * self.w2(x)
在 GLU Variants Improve Transformer 论文中,作者比较了各种GLU变体的激活函数,SwiGLU在各项任务上表现出众。但作者并未给出解释原因,只能说后验是这样,那就选它呗,所以成了LLM的标配。
各激活函数示意图
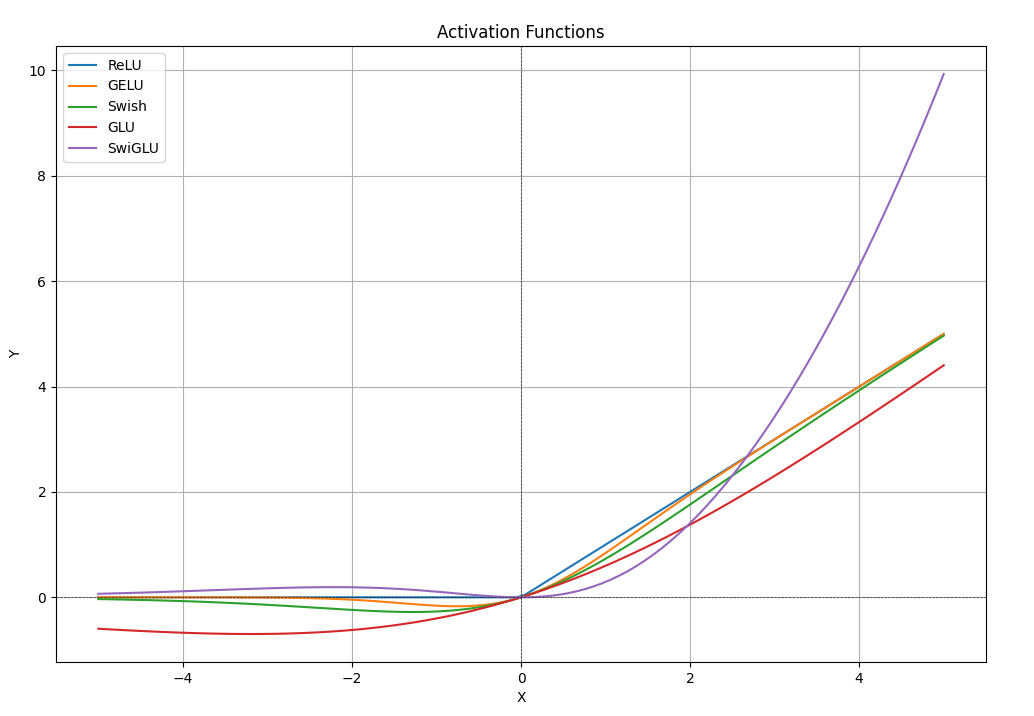
参考
- GLU Variants Improve Transformer
- SWISH: A SELF-GATED ACTIVATION FUNCTION
- 超越ReLU却鲜为人知,3年后被挖掘:BERT、GPT-2等都在用的激活函数
- 大模型基础|激活函数|从ReLU 到SwiGLU
相关文章:

SwiGLU激活函数
SwiGLU激活函数已经成为LLM的标配了。它是GLU的变体,公式如下: SwiGLU ( x , W , V , b , c , β ) Swish β ( x W b ) ⊗ ( x V c ) \operatorname{SwiGLU}(x, W, V, b, c, \beta)\operatorname{Swish}_\beta(x Wb) \otimes(x Vc) SwiGLU(x,…...

MySQL慢查询优化
当需要优化MySQL的慢查询时,通常需要结合多个方面进行分析和优化,包括索引优化、SQL语句重构、数据库结构调整等。下面,我将通过一个例子来说明如何优化MySQL的慢查询,包括多表关联和条件查询。 假设我们有一个简化的电子商务系统…...
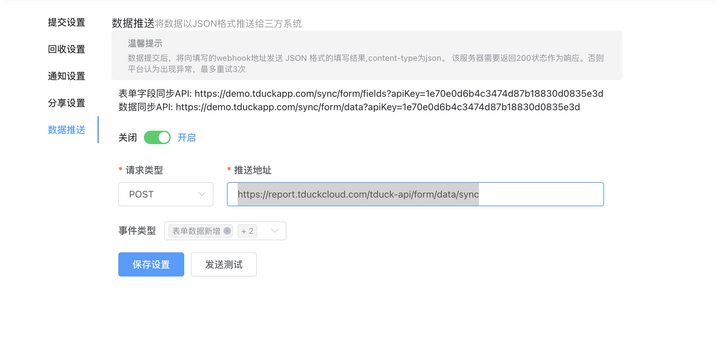
开源数据可视化大屏对接表单数据实践!
如果你需要一个表单系统,进行数据收集;可以使用tduck填鸭进行私有化部署,进行表单制作,完成数据收集。 在实际业务中,往往需要将收集的数据进行展示或分析;此时就可以使用表单数据推送到TReport中…...
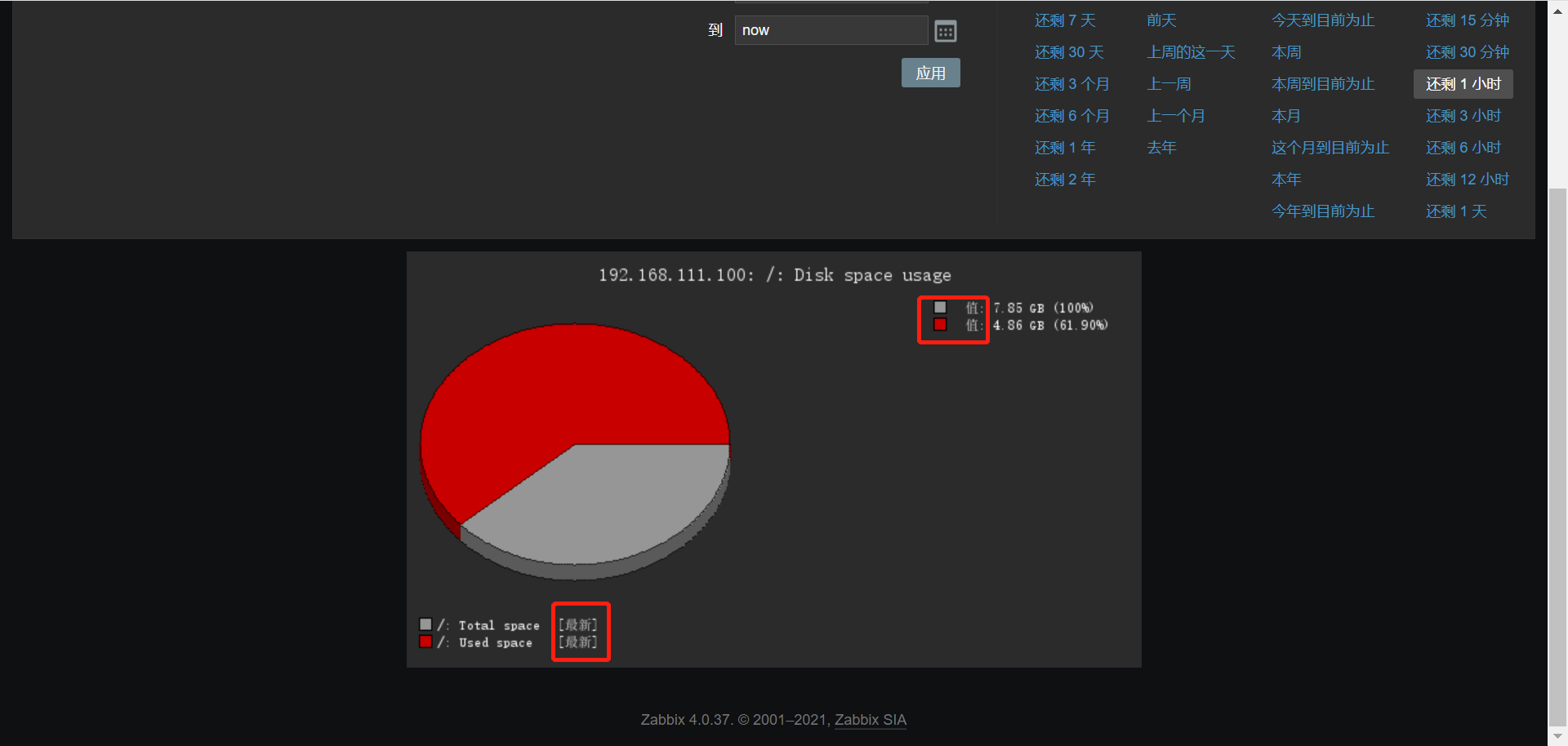
08.图形化界面字体问题处理
图形化界面字体问题处理 发现图形存在乱码,不显示文字 zabbix服务器的字符集所在的路径下: /usr/share/zabbix/assets/fonts 将本地windows系统的字体进行上传,选择一个自己喜欢的字体 上传到系统路径下并且直接覆盖掉 回到web浏览器界面…...

【代码随想录算法训练营第37期 第二天 | LeetCode977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵II】
代码随想录算法训练营第37期 第二天 | LeetCode977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵II 一、977.有序数组的平方 解题代码C: class Solution { public:vector<int> sortedSquares(vector<int>& nums) {int len nums.size();fo…...
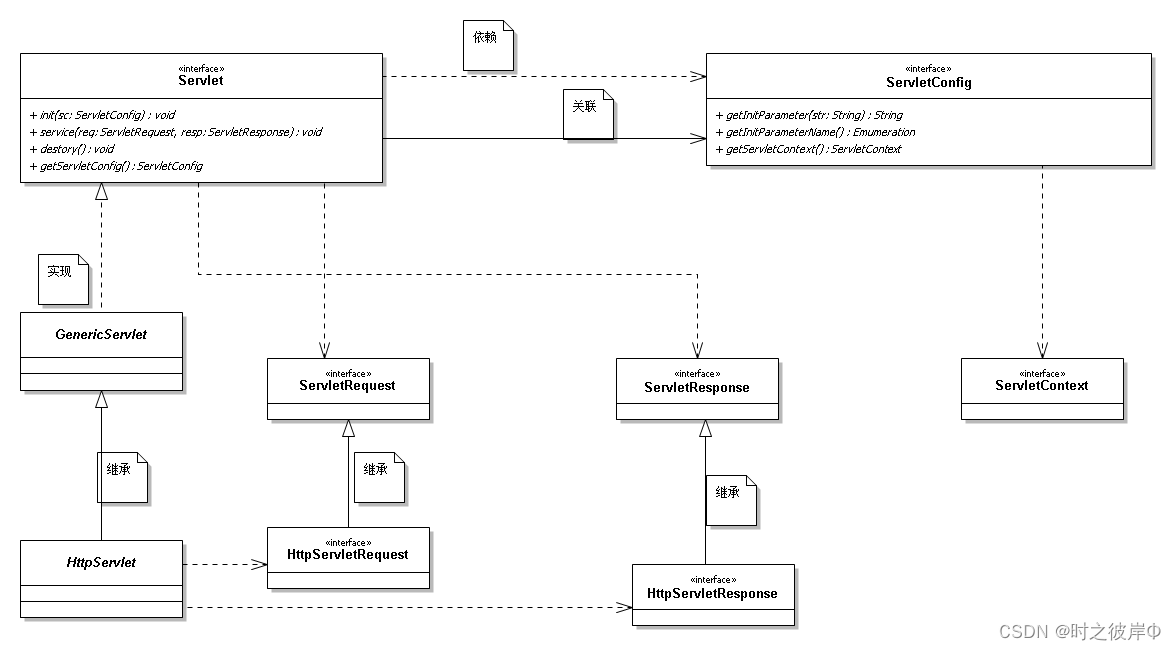
Java:Servlet详解
目录 一、什么是Servlet 二、Servlet原理 Servlet的生命周期 三、 Servlet注释 WebServlet 一、什么是Servlet Servlet是JavaWeb开发的一种技术,Servlet程序需要部署在Servlet容器(服务端)中才能运行,常见的Servlet容器有Tom…...

Oracle存储过程怎么定义类并继承
在Oracle数据库中,存储过程(Stored Procedure)是用于执行特定功能的预编译的SQL代码块。然而,Oracle的存储过程并不直接支持面向对象的编程概念,如类(Class)和继承(Inheritance&…...
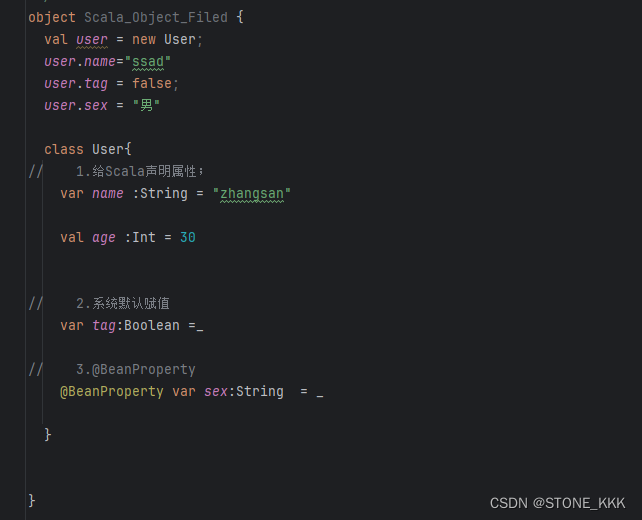
14_Scala面向对象编程_属性
文章目录 属性1.类中属性声明2.系统默认赋值3.BeanProperty4.整体代码如下 属性 1.类中属性声明 // 1.给Scala声明属性;var name :String "zhangsan"val age :Int 302.系统默认赋值 scala由于初始化变量必须赋值,为了解决此问题可以采…...

什么是网页反作弊
在搜索引擎技术中,网页反作弊是指一种防止网页排名被恶意操纵的技术。搜索引擎会根据特定的算法来评估网页的相关性和质量,以决定其在搜索结果中的排名。然而,有些人可能会尝试通过各种不正当的手段来提高自己网页的排名,这被称为…...

MAVEN打包JAR启动执行manifest
当您使用Maven进行项目打包,特别是需要创建一个可执行的JAR文件时,确保JAR文件的MANIFEST.MF中包含正确的Main-Class属性是非常重要的。这个属性告诉Java运行时环境哪个类包含main方法,作为应用程序的入口点。 如果您发现生成的JAR文件不包含…...
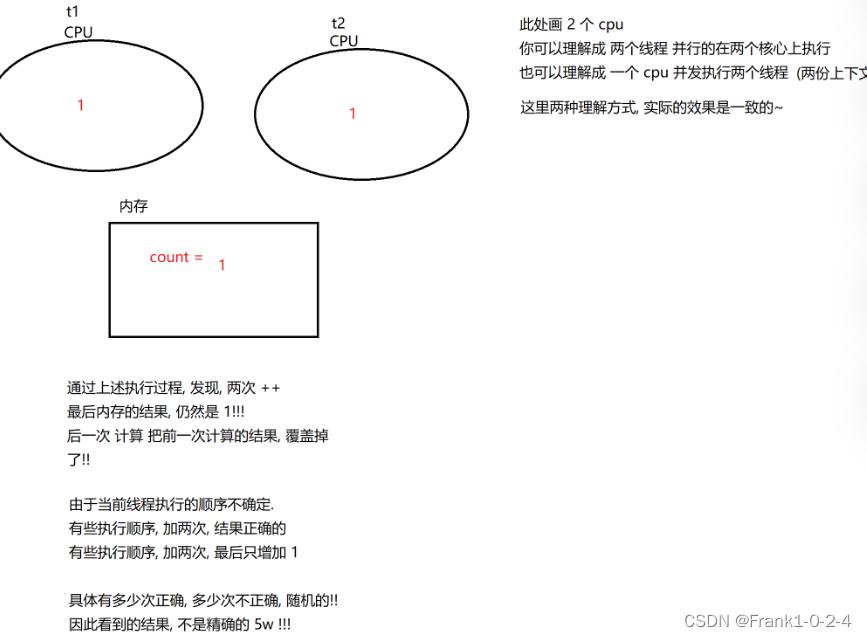
JavaEE 多线程详细讲解(1)
1.线程是什么 (shift F6)改类名 1.1.并发编程是什么 (1)当前的CPU,都是多核心CPU (2)需要一些特定的编程技巧,把要完成的仍无,拆解成多个部分,并且分别让…...
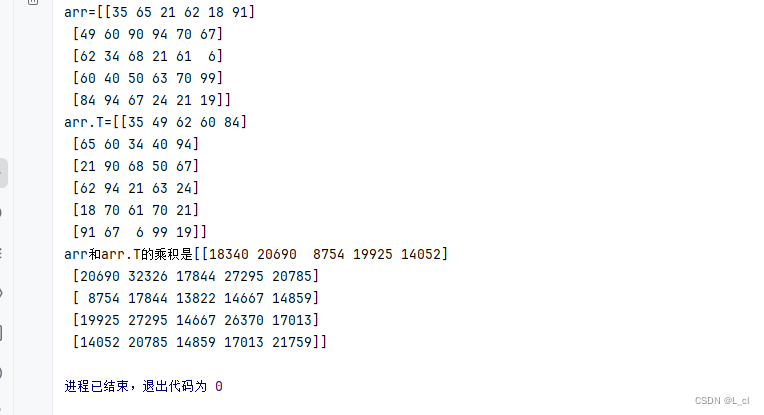
数据分析从入门到精通 1.numpy剑客修炼
会在某一瞬间突然明白,有些牢笼是自己给自己的 —— 24.5.5 一、数据分析秘笈介绍 1.什么是数据分析 是把隐藏在一些看似杂乱无章的数据背后的信息提炼出来,总结出所研究对象的内在规律。使得数据的价值最大化 案例: 分析用户的消…...

【iOS】KVO
文章目录 前言一、KVO使用1.基本使用2.context使用3.移除KVO通知的必要性4.KVO观察可变数组 二、代码调试探索1.KVO对属性观察2.中间类3.中间类的方法3.dealloc中移除观察者后,isa指向是谁,以及中间类是否会销毁?总结 三、KVO本质GNUStep窥探…...

python json字符串怎么用format方法填充参数值报KeyError
python json字符串怎么用format方法填充参数值报KeyError 需求问题分析解决方案 需求 因为python中的字典和json中的一些变量有差异,比如:json中有null、true,在python中就不会被识别,只能转换成字符串,在通过loads()…...

C++新手村指南:入门基础
目录 C概念 C发展史 C关键字(C98) 命名空间 命名空间的定义 命名空间的使用 C中的输入&&输出 缺省参数 缺省参数的概念 缺省参数的分类 函数重载 函数重载概念 函数重载实现 引用 引用的概念 引用的特性 常引用 引用的使用场景…...

智慧旅游推动旅游服务智慧化转型:借助智能科技的力量,实现旅游资源的精准匹配和高效利用,为游客提供更加便捷、舒适的旅游环境
目录 一、引言 二、智慧旅游的定义与特点 (一)智慧旅游的定义 (二)智慧旅游的特点 三、智能科技在旅游服务中的应用 (一)大数据分析助力旅游决策 (二)人工智能实现个性化推荐…...

Hikyuu-PF-银行股轮动交易策略实现
今天,带来的是“如何使用 Hikyuu 中的投资组合来实现银行股轮动交易策略”。 这个策略的逻辑很简单:持续持有两支市净率最低银行股,然后每月换仓 定义回测周期与回测标的 同样,首先定义回测周期: # 定义回测日期 …...
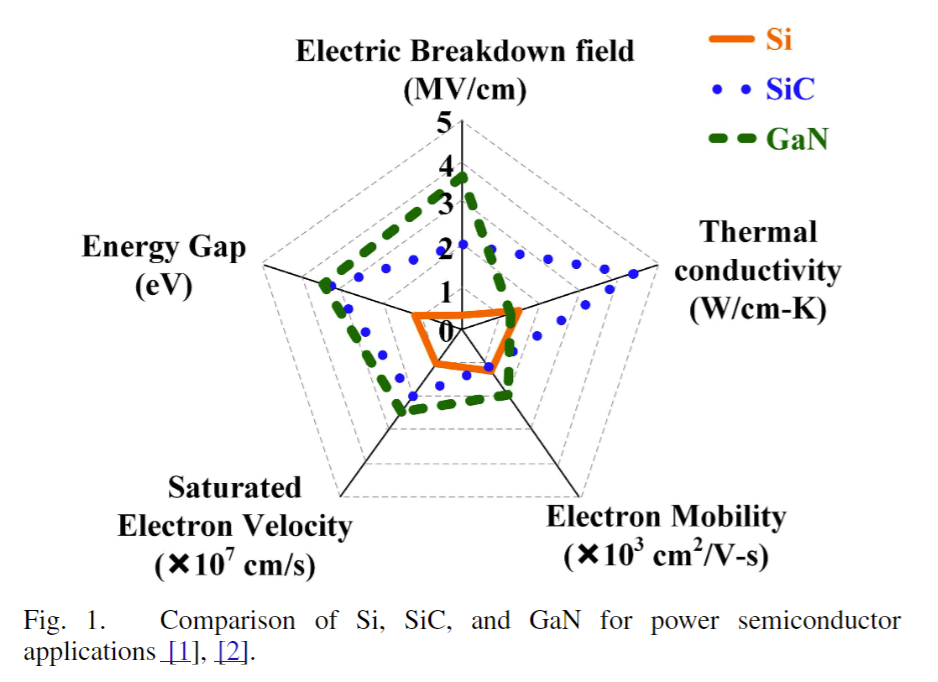
【氮化镓】GaN功率器件在转换器设计中的挑战
I. 引言(INTRODUCTION) 宽带隙(WBG)器件的重要性: 引言部分首先强调了宽带隙(WBG)器件在高频、高效率电力电子技术中的关键作用。这些器件,包括碳化硅(SiC)和氮化镓(GaN),相较于传统的硅功率器件,具有显著的优势。宽带隙半导体材料的高击穿场强允许设计更薄的漂…...
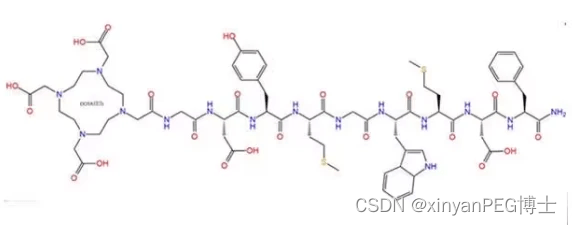
DOTA-Gly-Asp-Tyr-Met-Gly-Trp-Met-Asp-Phe-NH2,1306310-00-8,是一种重要的多肽化合物
一、试剂信息 名称:DOTA-Gly-Asp-Tyr-Met-Gly-Trp-Met-Asp-Phe-NH2CAS号:1306310-00-8结构式: 二、试剂内容 DOTA-Gly-Asp-Tyr-Met-Gly-Trp-Met-Asp-Phe-NH2是一种重要的多肽化合物,其CAS号为1306310-00-8。该多肽包含一个DO…...

CopyClip for Mac - 高效复制粘贴,轻松管理剪贴板
CopyClip for Mac,一款专为Mac用户打造的剪贴板管理工具,让你在复制粘贴的日常任务中,享受到前所未有的高效与便捷。 它常驻在菜单栏中,时刻准备为你服务。一旦你复制了内容,CopyClip就会自动将其保存至历史记录中&…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
