【R语言】边缘概率密度图
边缘概率密度图是一种在多变量数据分析中常用的图形工具,用于显示每个单独变量的概率密度估计。它通常用于散点图的边缘,以便更好地理解单个变量的分布情况,同时保留了散点图的相关性信息。
在边缘概率密度图中,每个变量的概率密度估计通常通过直方图或核密度估计(KDE)进行计算。直方图将变量的值范围分成若干个区间,并统计每个区间中观察值的数量,然后将数量除以总观察值数量得到概率密度。而核密度估计则是通过在每个数据点周围放置核函数,并根据核函数的形状和宽度来估计概率密度。
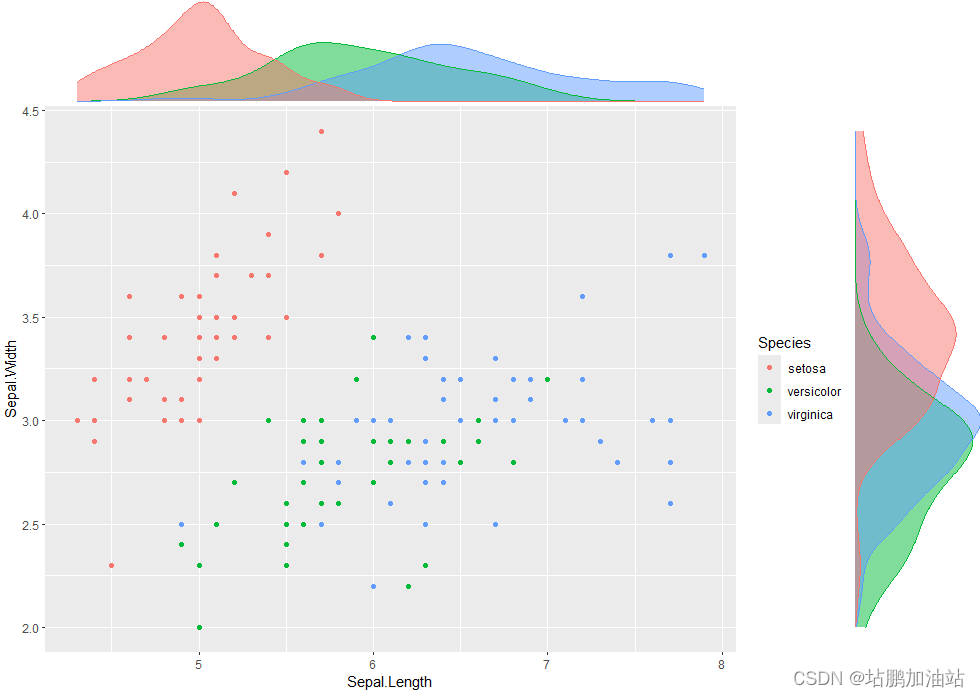
边缘概率密度图通常与散点图一起显示,其中散点图展示了两个变量之间的关系,而边缘概率密度图则展示了每个变量的分布情况。这有助于发现变量之间的相关性以及每个变量的个体特征。如下图所示:
 代码如下:
代码如下:
library("ggExtra")
library("ggplot2")piris <- ggplot(iris, aes(Sepal.Length, Sepal.Width, colour = Species)) +geom_point()
ggMarginal(piris, groupColour = TRUE, groupFill = TRUE)
piris <- ggplot(iris, aes(Sepal.Length, Sepal.Width, colour = Species)) + geom_point():首先,创建了一个散点图piris,其中 x 轴表示 Sepal.Length(花萼长度),y 轴表示 Sepal.Width(花萼宽度),并根据 Species(鸢尾花种类)变量进行颜色编码。
ggMarginal(piris, groupColour = TRUE, groupFill = TRUE):然后,使用ggMarginal()函数对piris图进行了包装,以创建带有边际图的散点图。参数groupColour = TRUE和groupFill = TRUE用于在边际图中反映颜色组。这意味着对于每个不同的鸢尾花种类,都会生成一个单独的边际图,以反映该组中的数据分布情况。
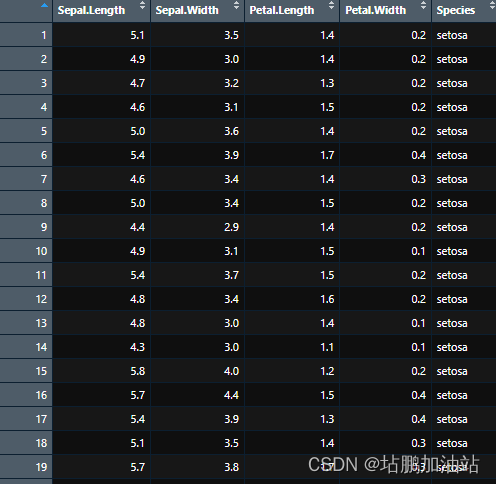
iris的数据集形式如下:
相关文章:

【R语言】边缘概率密度图
边缘概率密度图是一种在多变量数据分析中常用的图形工具,用于显示每个单独变量的概率密度估计。它通常用于散点图的边缘,以便更好地理解单个变量的分布情况,同时保留了散点图的相关性信息。 在边缘概率密度图中,每个变量的概率密度…...

中国结(科普)
中国结是一种手工编织工艺品,它身上所显示的情致与智慧正是汉族古老文明中的一个侧面。 [1]它原本是由旧石器时代的缝衣打结,后推展至汉朝的仪礼记事,再演变成今日的装饰手艺。周朝人随身的佩戴玉常以中国结为装饰,而战国时代的铜…...

使用Android Studio 搭建AOSP FrameWork 源码阅读开发环境
文章目录 概述安装Android Studio编译源码使用Android Studio打开源码制作ipr文件直接编译成功后自动打开Android Studio 修改SystemUI验证开发环境 概述 我们都知道Android的系统源码量非常之大,大致有frameworka层源码,硬件层(HAL)源码,内…...
区块链 | IPFS:CID
🦊原文:Anatomy of a CID 🦊写在前面:本文属于搬运博客,自己留存学习。 1 CID 在分布式网络中与其他节点交换数据时,我们依赖于内容寻址(而不是中心化网络的位置寻址)来安全地定位…...
PostgreSQL(十二)报错:Tried to send an out-of-range integer as a 2-byte value: 51000
目录 一、报错场景二、源码分析三、实际原因(更加复杂)四、解决思路 一、报错场景 今天写了一个历史数据处理程序,在开发环境、测试环境都可以正常执行,但是放到生产环境上就不行,报了一个这样的错误: or…...

Linux守护进程
进程组和会话在 UNIX 系统中是非常重要的概念,特别是在进行作业控制和终端会话管理时。下面是关于进程组和会话的详细解释: 进程组(Process Group) 定义与作用: 进程组是一个或多个进程的集合,这些进程通常…...
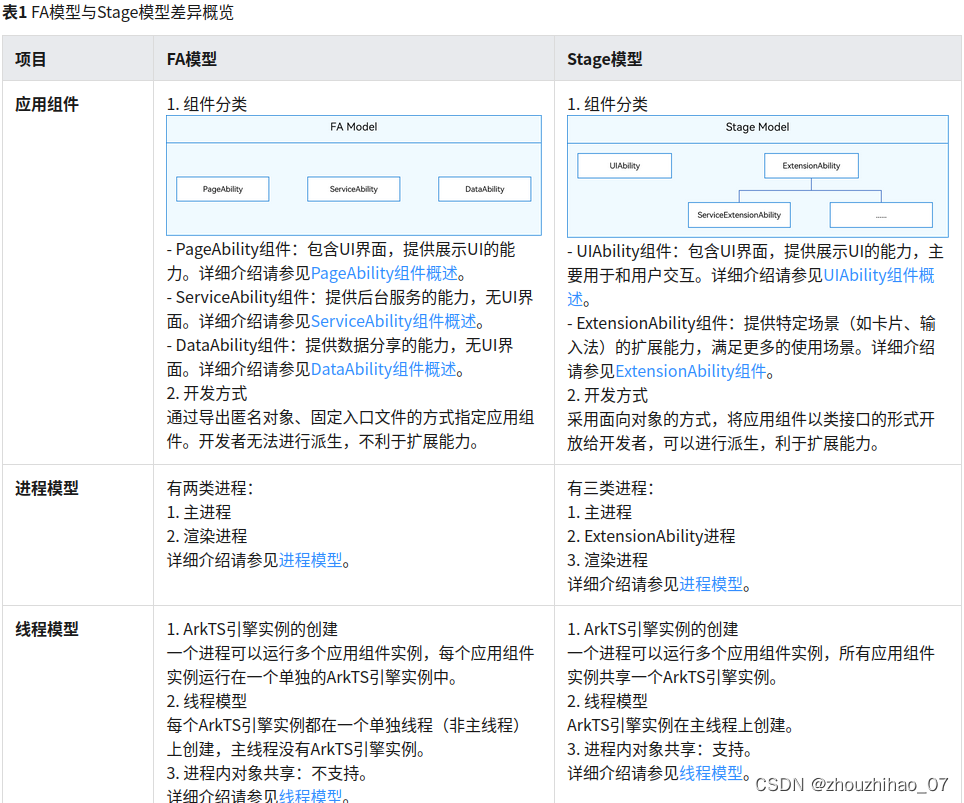
HarmonyOS 应用开发——入门
首先当然是华为的官方文档了,要认真学习: https://developer.huawei.com/consumer/cn/doc/harmonyos-guides-V2/start-overview-0000001478061421-V2 不想花时间看,可以看我下面总结的干货,哈哈 第一个问题:stage架构和fa架构的区…...
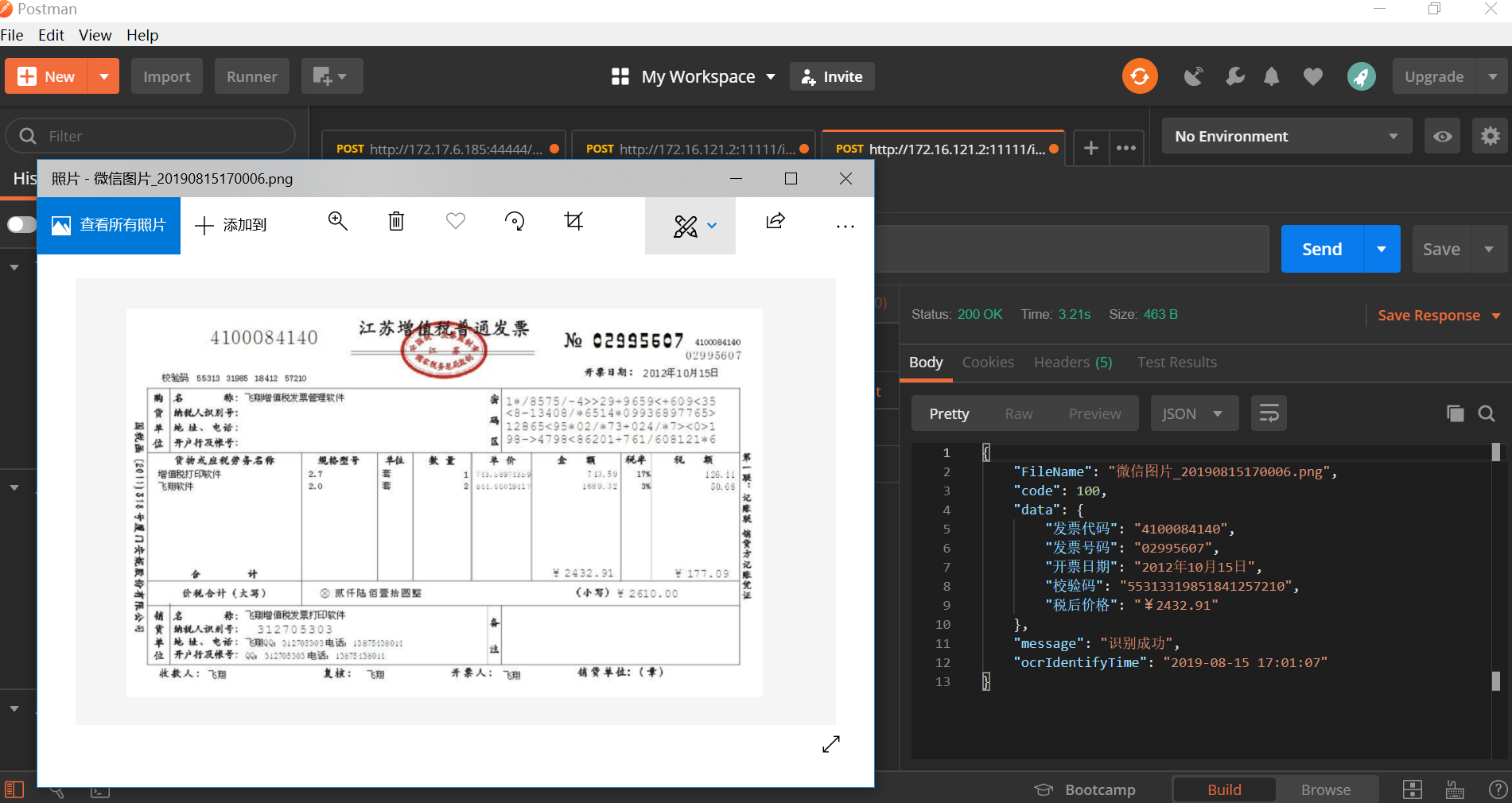
开源免费的发票识别OCR应用:Invoice
Invoice:轻松识别,发票电子化扫描烦恼消- 精选真开源,释放新价值。 概览 Invoice 是github社区上一个采用开源许可协议发布的增值税发票光学字符识别(OCR)解决方案项目。该项目不仅集成了预训练的高级模型,…...

关于Docker alpine
1.拉取alpine镜像 docker pull alpine 2.运行镜像成为容器 docker run -it --rm alpine sh (--rm标志确保容器在退出时被自动删除。) 3.容器建立后,运行 docker exec -it <container_id> sh 4.进入容器里的 alpine环境 ①.配置安装源 cat >/etc…...

【Elasticsearch运维系列】Elasticsearch7.12.1启动指定版本JDK:你学废了吗?
一、背景 一套生ES集群,版本为7.12.1,近期频繁告警,频繁出现索引分片异常,索引状态异常,导致应用无法正常写入ES,另外,也经常出现节点掉问题。通过分析相关ES日志,显示和当前JAVA G…...
思通数科大模型在智能数据查询系统中的深度应用:销售数据分析的革新
在企业决策支持系统中,销售数据分析占据着举足轻重的地位。思通数科的大模型技术,结合自然语言处理(NLP)和机器学习,为智能数据查询系统提供了强大的分析能力。本文将详细描述思通数科大模型在销售数据分析中的应用&am…...
上位机图像处理和嵌入式模块部署(树莓派4b和qt应用全屏占有)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 我们都知道,嵌入式应用一般都是为了某一个特定应用而存在的。也就是说,和pc不同,这个嵌入式板子一般都是为了解…...
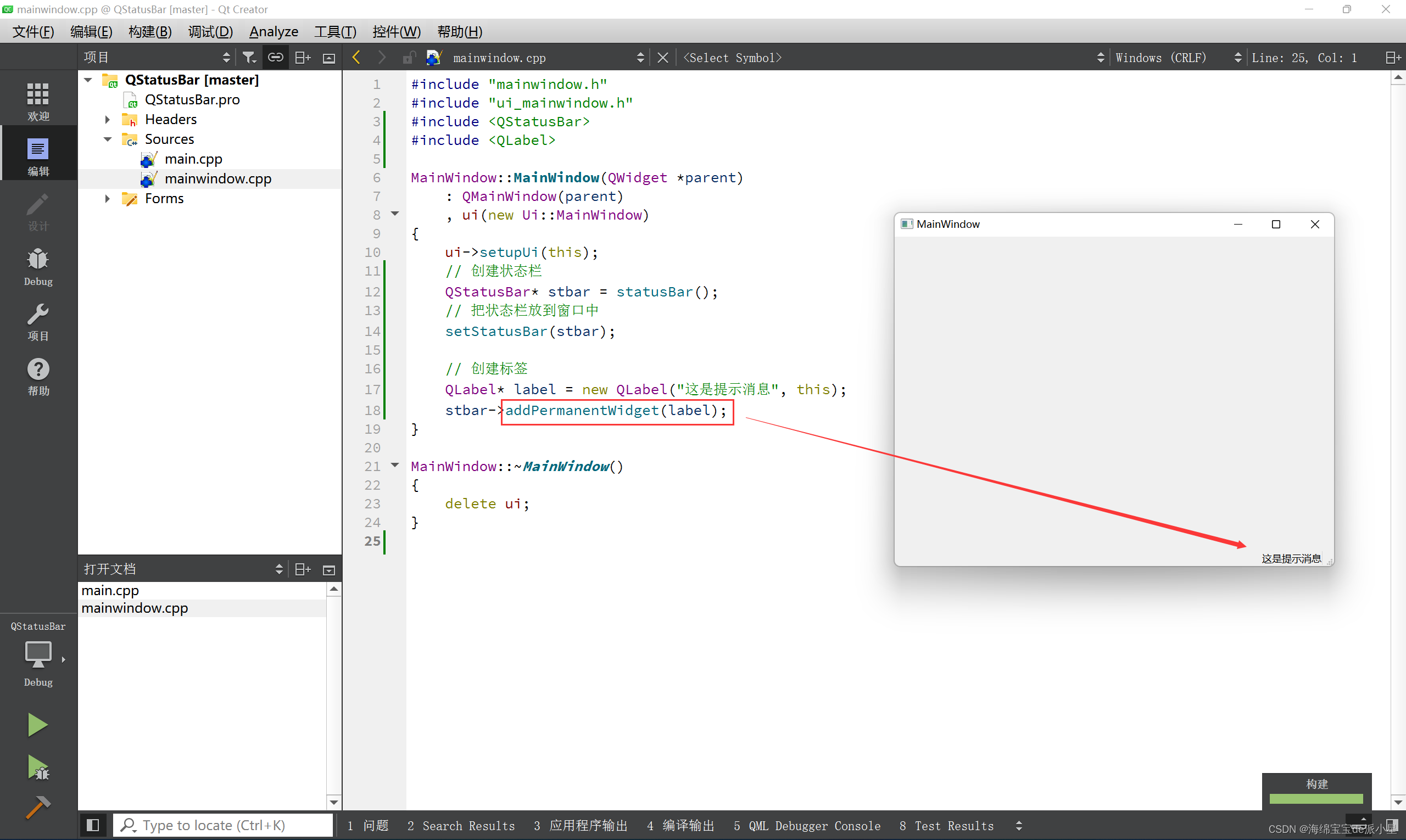
QT:QT窗口(一)
文章目录 菜单栏创建菜单栏在菜单栏中添加菜单创建菜单项添加分割线 工具栏创建工具栏设置停靠位置创建工具栏的同时指定停靠位置使用QToolBar类提供的setAllowedAreas函数来设置停靠位置 设置浮动属性设置移动属性 状态栏状态栏的创建在状态栏中显示实时消息在状态栏中显示永久…...

matlab例题大全
1.第1章 MATLAB系统环境 1.1 注:plot函数为画图函数。例plot(x1,y1,:,x2,y2,*); 1.2 注:root为求根函数。p为方程变量前面系数矩阵。 1.3 注: 2*x3y-1*z 2; 8*x2*y3*z 4; 45*x3*y9*z 23 求:x,y,z的…...
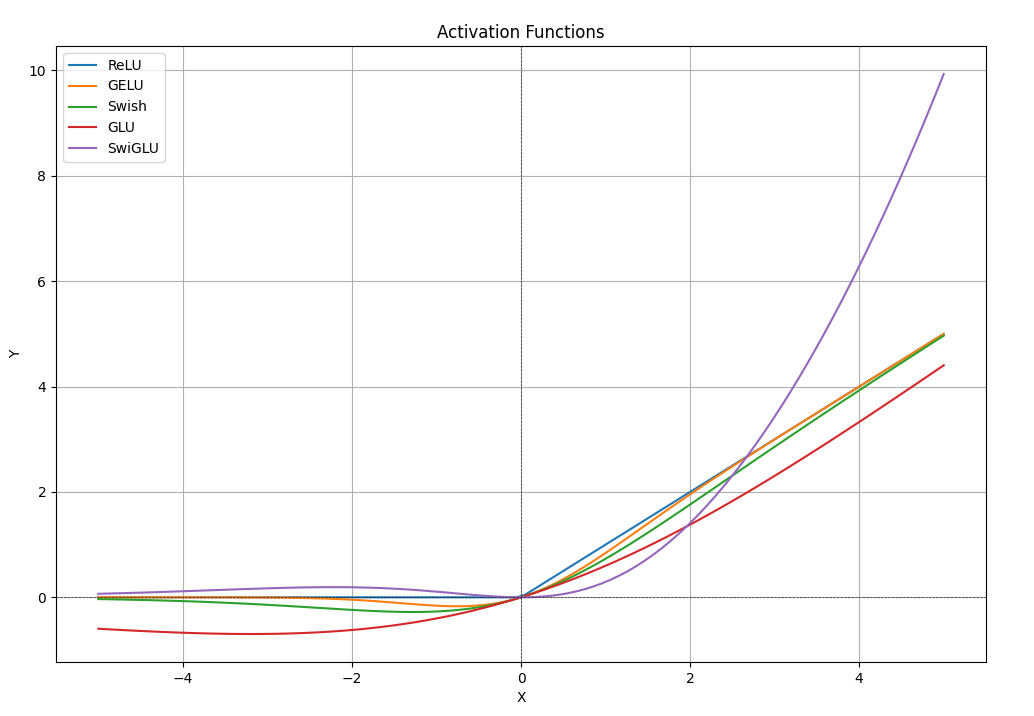
SwiGLU激活函数
SwiGLU激活函数已经成为LLM的标配了。它是GLU的变体,公式如下: SwiGLU ( x , W , V , b , c , β ) Swish β ( x W b ) ⊗ ( x V c ) \operatorname{SwiGLU}(x, W, V, b, c, \beta)\operatorname{Swish}_\beta(x Wb) \otimes(x Vc) SwiGLU(x,…...

MySQL慢查询优化
当需要优化MySQL的慢查询时,通常需要结合多个方面进行分析和优化,包括索引优化、SQL语句重构、数据库结构调整等。下面,我将通过一个例子来说明如何优化MySQL的慢查询,包括多表关联和条件查询。 假设我们有一个简化的电子商务系统…...
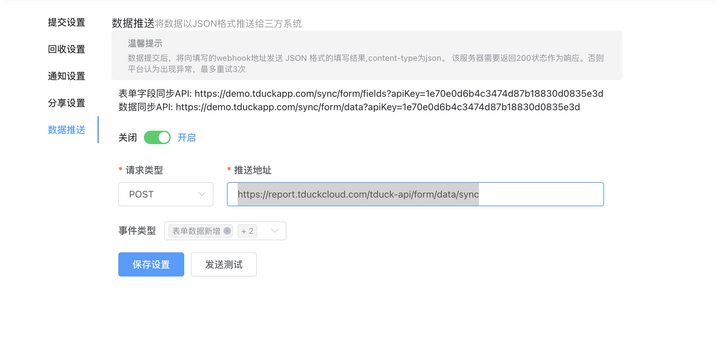
开源数据可视化大屏对接表单数据实践!
如果你需要一个表单系统,进行数据收集;可以使用tduck填鸭进行私有化部署,进行表单制作,完成数据收集。 在实际业务中,往往需要将收集的数据进行展示或分析;此时就可以使用表单数据推送到TReport中…...
08.图形化界面字体问题处理
图形化界面字体问题处理 发现图形存在乱码,不显示文字 zabbix服务器的字符集所在的路径下: /usr/share/zabbix/assets/fonts 将本地windows系统的字体进行上传,选择一个自己喜欢的字体 上传到系统路径下并且直接覆盖掉 回到web浏览器界面…...

【代码随想录算法训练营第37期 第二天 | LeetCode977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵II】
代码随想录算法训练营第37期 第二天 | LeetCode977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵II 一、977.有序数组的平方 解题代码C: class Solution { public:vector<int> sortedSquares(vector<int>& nums) {int len nums.size();fo…...
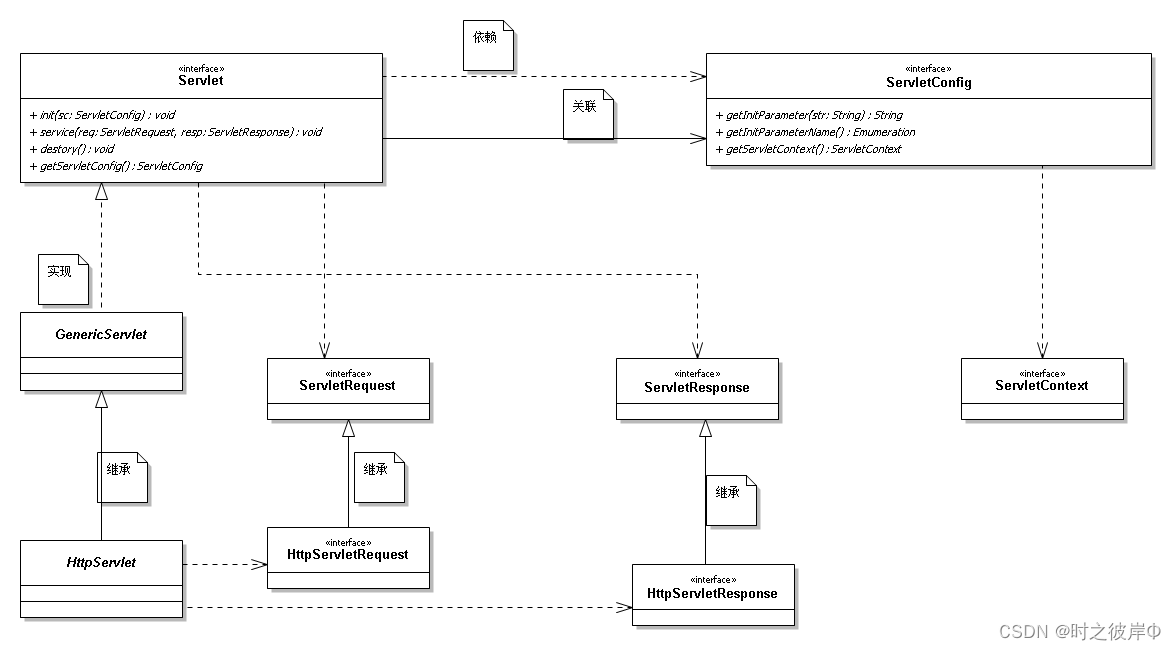
Java:Servlet详解
目录 一、什么是Servlet 二、Servlet原理 Servlet的生命周期 三、 Servlet注释 WebServlet 一、什么是Servlet Servlet是JavaWeb开发的一种技术,Servlet程序需要部署在Servlet容器(服务端)中才能运行,常见的Servlet容器有Tom…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
