95、动态规划-编辑距离
递归暴力解法
递归方法的基本思想是考虑最后一个字符的操作,然后根据这些操作递归处理子问题。
递归函数定义:定义一个递归函数 minDistance(i, j),表示将 word1 的前 i 个字符转换成 word2 的前 j 个字符所需的最小操作数。
递归终止条件:
- 如果
i == 0,意味着word1为空,此时将word1转换成word2的前j个字符就需要j次插入操作。 - 如果
j == 0,意味着word2为空,此时将word1的前i个字符转换成空字符串需要i次删除操作。
递归转移方程:
- 如果
word1[i-1] == word2[j-1],则当前两个字符相等,不需要操作,所以minDistance(i, j) = minDistance(i-1, j-1)。 - 如果不相等,则可以进行插入、删除或替换操作,转移方程为:
- 插入:
minDistance(i, j) = minDistance(i, j-1) + 1 - 删除:
minDistance(i, j) = minDistance(i-1, j) + 1 - 替换:
minDistance(i, j) = minDistance(i-1, j-1) + 1
- 插入:
- 取三者的最小值。
代码如下:
public class Solution {// 主方法,用于外部调用,传入两个字符串public int minDistance(String word1, String word2) {// 调用递归助手函数,初始化i和j为字符串的长度,从字符串尾部开始比较return minDistanceHelper(word1, word2, word1.length(), word2.length());}// 递归助手函数,用于计算两个字符串的最小编辑距离private int minDistanceHelper(String word1, String word2, int m, int n) {// 如果第一个字符串为空,则转换的代价是第二个字符串的长度(即插入n次)if (m == 0) return n;// 如果第二个字符串为空,则转换的代价是第一个字符串的长度(即删除m次)if (n == 0) return m;// 如果两个字符串的当前字符相等,则不需要操作,递归考虑前一个字符if (word1.charAt(m - 1) == word2.charAt(n - 1)) {return minDistanceHelper(word1, word2, m - 1, n - 1);}// 计算插入操作的代价:将word2的第n个字符插入到word1的末尾,然后继续处理剩余的字符串int insert = minDistanceHelper(word1, word2, m, n - 1) + 1;// 计算删除操作的代价:删除word1的第m个字符,然后继续处理剩余的字符串int delete = minDistanceHelper(word1, word2, m - 1, n) + 1;// 计算替换操作的代价:将word1的第m个字符替换为word2的第n个字符,然后继续处理剩余的字符串int replace = minDistanceHelper(word1, word2, m - 1, n - 1) + 1;// 返回三种操作中的最小值,即为到当前位置为止的最小编辑距离return Math.min(Math.min(insert, delete), replace);}
}
但是重复计算效率很慢,改成动态规划:
动态规划方法
动态规划方法的核心思想是使用一个二维数组 dp 来存储中间结果,其中 dp[i][j] 表示将 word1 的前 i 个字符转换成 word2 的前 j 个字符所需的最小操作数。通过填充这个数组,我们可以逐步构建出从一个空字符串到完整 word2,再从完整 word1 到 word2 的转换路径。
初始化:
dp[0][j]:将空字符串转换为word2的前j个字符,需要j次插入操作。dp[i][0]:将word1的前i个字符转换为空字符串,需要i次删除操作。
状态转移方程:
- 如果
word1[i-1] == word2[j-1],则dp[i][j] = dp[i-1][j-1],因为最后一个字符已经匹配,不需要额外操作。 - 如果
word1[i-1] != word2[j-1],则可以从以下三个可能的操作中选择最小成本的:- 插入:
dp[i][j] = dp[i][j-1] + 1 - 删除:
dp[i][j] = dp[i-1][j] + 1 - 替换:
dp[i][j] = dp[i-1][j-1] + 1
- 插入:
代码如下:
public class Solution {public int minDistance(String word1, String word2) {int m = word1.length();int n = word2.length();int[][] dp = new int[m + 1][n + 1];// 初始化dp数组for (int i = 0; i <= m; i++) {dp[i][0] = i; // 从word1的i字符变为空字符串}for (int j = 0; j <= n; j++) {dp[0][j] = j; // 从空字符串变为word2的j字符}// 填充dp数组for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i-1][j-1];} else {dp[i][j] = Math.min(Math.min(dp[i-1][j] + 1, dp[i][j-1] + 1), dp[i-1][j-1] + 1);}}}return dp[m][n];}
}
相关文章:

95、动态规划-编辑距离
递归暴力解法 递归方法的基本思想是考虑最后一个字符的操作,然后根据这些操作递归处理子问题。 递归函数定义:定义一个递归函数 minDistance(i, j),表示将 word1 的前 i 个字符转换成 word2 的前 j 个字符所需的最小操作数。 递归终止条件…...

linux调试
文章目录 1. 使用打印来调试1.1 重定向1.2 标准预定义宏1.3 日志代码 2. 内核异常2.1 内核打印2.1.1 打印级别2.1.2 跟踪异常2.1.3 动态打印2.1.4 RAM console 2.2 OOPS2.2.1 有源代码的情况2.2.2 没有源代码的情况 3 查看日志4 工具调试 1. 使用打印来调试 1.1 重定向 2>…...
【C++】string类的使用②(容量接口Capacity || 元素获取Element access)
🔥个人主页: Forcible Bug Maker 🔥专栏: STL || C 目录 前言🔥容量接口(Capacity)size和lengthcapacitymax_sizereserveresizeclearemptyshrink_to_fit 🔥元素获取(Ele…...
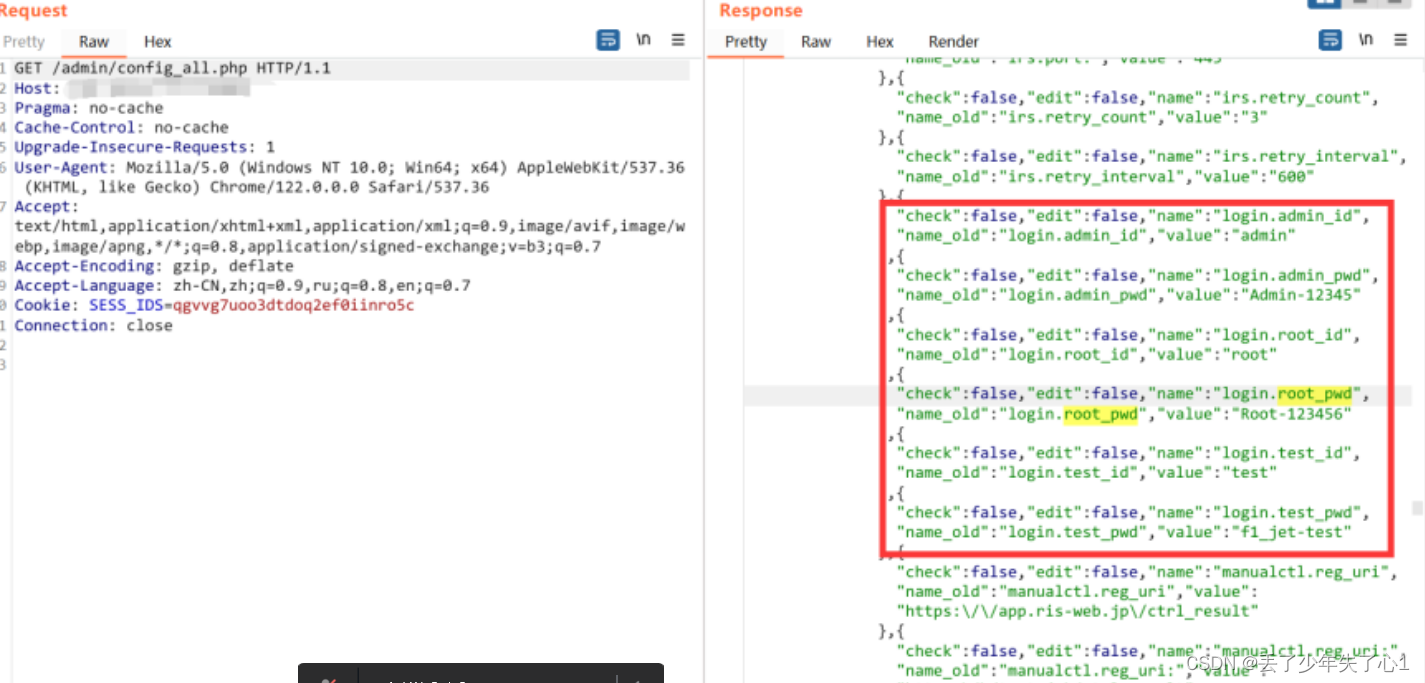
【漏洞复现】某小日子太阳能系统DataCube3审计
漏洞描述 某小日子太阳能系统DataCube3终端测量系统 多个漏洞利用方式 免责声明 技术文章仅供参考,任何个人和组织使用网络应当遵守宪法法律,遵守公共秩序,尊重社会公德,不得利用网络从事危害国家安全、荣誉和利益,未经授权请勿利用文章中的技术资料对任何计算机系统进…...

探索Java的未来
目录 一、云计算与大数据 二、人工智能与机器学习 三、物联网与边缘计算 四、安全性与性能优化 五、社区与生态 Java,作为一种广泛使用的编程语言,自其诞生以来就以其跨平台性、面向对象特性和丰富的库资源赢得了开发者的青睐。然而,随着…...
Web3 ETF软件开发
开发Web3 ETF软件涉及到金融、法律和技术等多个领域的专业知识,因此存在以下技术难点,开发Web3 ETF软件是一项复杂的技术挑战,需要综合考虑各种因素。开发人员需要具备较强的技术能力和跨学科知识才能成功开发Web3 ETF软件。北京木奇移动技术…...

初始MySQL
初始化MySQL数据库通常涉及以下步骤: 下载并安装MySQL: 你可以从MySQL官方网站下载适合你的操作系统的MySQL安装包。安装时,遵循安装向导的步骤,通常包括选择安装位置、选择组件(例如MySQL服务器、MySQL Workbench等&a…...
)
STM32项目下载清单(不定时更新)
收集的一些资料,分享下载 电赛一等奖作品,老人健康监测智能手表(STM32F4主控) STM32数字示波器源码数字信号处理教程、配套实例基于stm32 nucleo_L476的智能灯(操作说明源码)基于STM32 NUCLEO板设计彩色LE…...

thinkphp5 配合阿里直播实现直播功能流程
要为你提供一个更详细的教程来结合ThinkPHP 5和阿里直播SDK实现直播功能,需要涵盖的内容相对较多。不过,我可以为你提供一个大致的、更详细的步骤指南,供你参考和扩展: 1. 准备工作 a. 注册阿里云账号 前往阿里云官网注册账号&…...

安卓手机APP开发__媒体3格式转换器__常见问题解答
安卓手机APP开发__媒体3格式转换器__常见问题解答 目录 1 为什么在示例的APP中我不能读取到本地的文件? 2 在一个特定的设备为什么导出失败? 3 媒体3格式转换器支持转码(或者是录制)远程的媒体吗? 4 媒体3格式转换…...
leetcode-有重复数字的全排列-98
题目要求 思路 1.同【没有重复项的全排列-97】这个题一样,都是递归的题,区别在于这个可能会包含重复的数字,因此,不能只是简单的通过两个值是否相等然后用标志位标记,而是新增了一个数组,这个数组专门用于…...
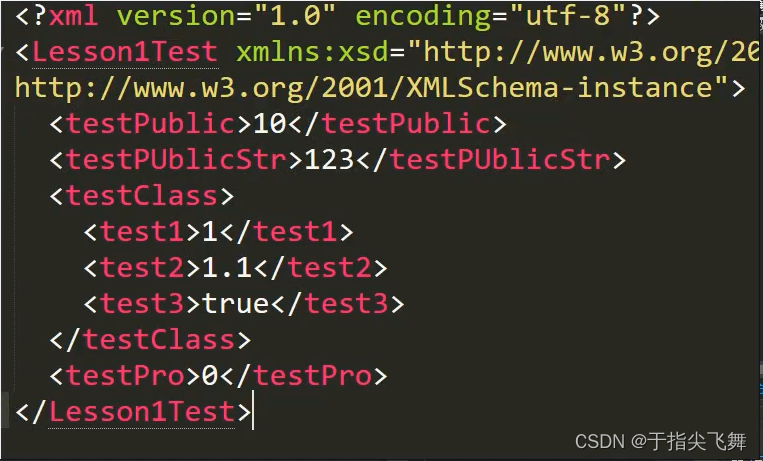
Unity数据持久化之XML
目录 数据持久化XML概述XML文件格式XML基本语法XML属性 C#读取存储XMLXML文件存放位置C#读取XML文件C#存储XML文件 实践小项目必备知识点XML序列化(不支持字典)XML反序列化IXmlSerializable接口让Dictionary支持序列化反序列化 数据持久化XML概述 什么是…...

Leetcode 226:翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 思路:使用递归 //使用前序遍历翻转树public static TreeNode invertTree(TreeNode root){if(rootnull) return root;swap(root);invertTree(root.left);invertTree(root.rig…...

柯里化与无参装饰器
柯里化 柯里化的概念:柯里化(Currying)在Python中是一种编程技术,它将原本接受多个参数的函数转换为一系列接受单个参数的函数。这种方法以逻辑学家Haskell Curry的名字命名。 简而言之就是将一次函数调用变成先放入一个参数得到…...

Spring事务失效的场景
1. 事务方法执行期间出现了异常,但是并未指定rollbackFor: Spring默认只会在遇到error和RunTimeException时才会回滚。 public boolean rollbackon ( Throwable ex){return (ex instanceof RuntimeException || ex instanceof Error); } 2. 事务方法执行期间出现了…...

Python基础学习之datetime模块
在Python编程中,处理日期和时间是一个常见的需求。Python的datetime模块提供了丰富的类和方法,用于表示和操作日期、时间、时间间隔等。本文将详细介绍Python的datetime模块,并给出一些实用的示例。 1. datetime模块概览 datetime模块是Pyt…...

在AI大模型中全精度和半精度参数是什么意思?
环境: 大模型中 问题描述: 在AI大模型中全精度和半精度参数是什么意思? 解决方案: 在深度学习和高性能计算领域,"全精度"和"半精度"通常指的是模型中使用的数值表示的精度,具体涉…...

刷题记录2
文章目录 刷题记录21047.删除字符串中的所有相邻重复项150.逆波兰表达式求值239.滑动窗口最大值347.前k个高频元素144.二叉树前序遍历(145、94后序、中序)102.二叉树的层序遍历226.翻转二叉树101.对称二叉树104.二叉树的最大深度111.二叉树的最小深度222.完全二叉树的节点个数 …...

【配置】Docker搭建JSON在线解析网站
一个python朋友需要,顺便做一下笔记 正常用菜鸟的就够了,点下面 JSON在线解析 云服务器打开端口8787 连接上docker运行 docker run -id --name jsonhero -p 8787:8787 -e SESSION_SECRETabc123 henryclw/jsonhero-webhttp://ip:8787访问 Github&…...

2024.5.2 —— LeetCode 高频题复盘
目录 151. 反转字符串中的单词129. 求根节点到叶节点数字之和104. 二叉树的最大深度101. 对称二叉树110. 平衡二叉树144. 二叉树的前序遍历543. 二叉树的直径48. 旋转图像98. 验证二叉搜索树39. 组合总和 151. 反转字符串中的单词 题目链接 class Solution:def reverseWords(s…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
