第 129 场 LeetCode 双周赛题解
A 构造相同颜色的正方形
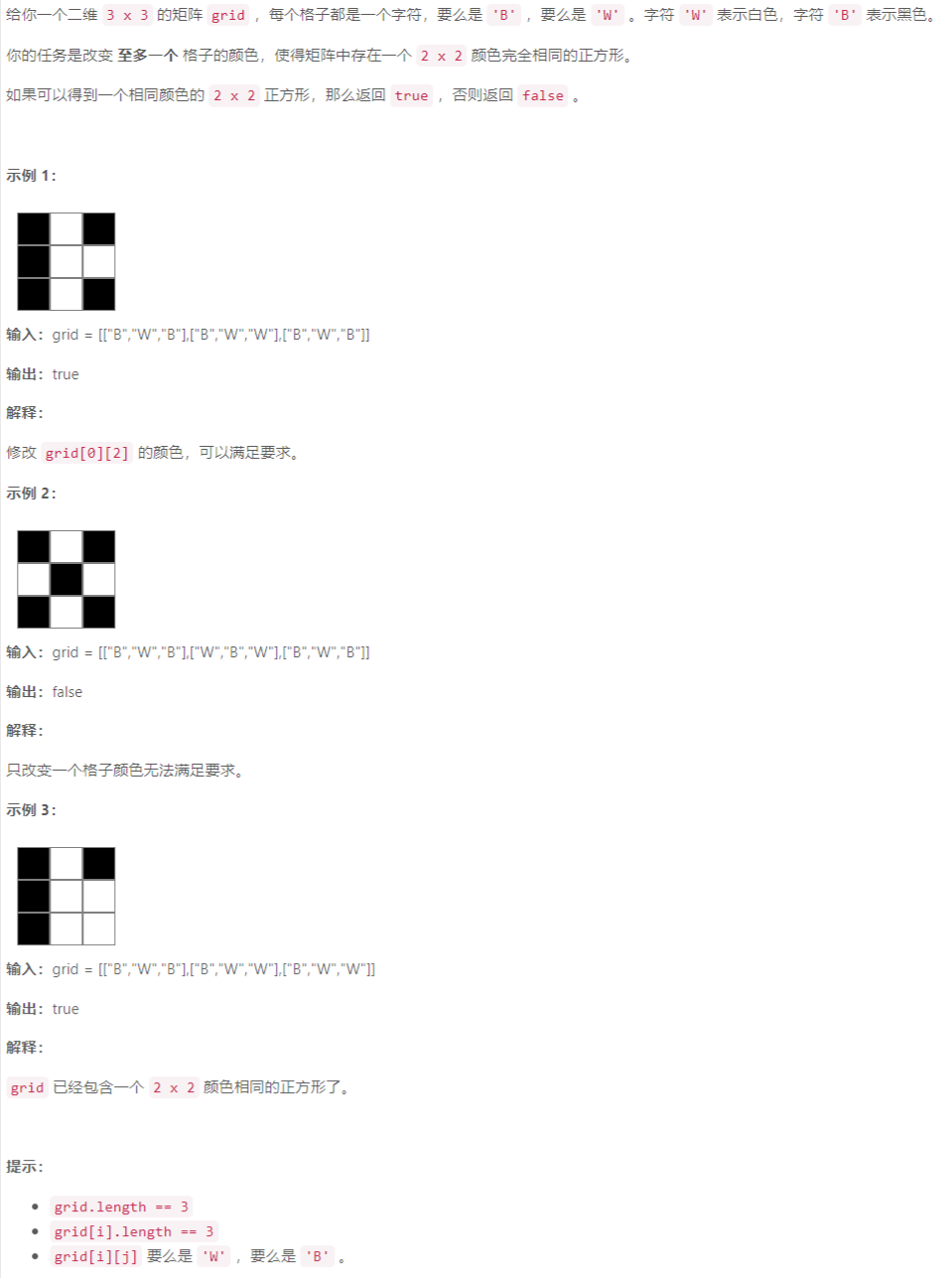
枚举:枚举每个 3 × 3 3\times 3 3×3的矩阵,判断是否满足条件
class Solution {public:bool canMakeSquare(vector<vector<char>>& grid) {for (int i = 0; i < 2; i++)for (int j = 0; j < 2; j++) {int c1 = 0, c2 = 0;for (int r = 0; r < 2; r++)for (int c = 0; c < 2; c++)if (grid[i + r][j + c] == 'B')c1++;elsec2++;if (max(c1, c2) >= 3)return true;}return false;}
};
B 直角三角形
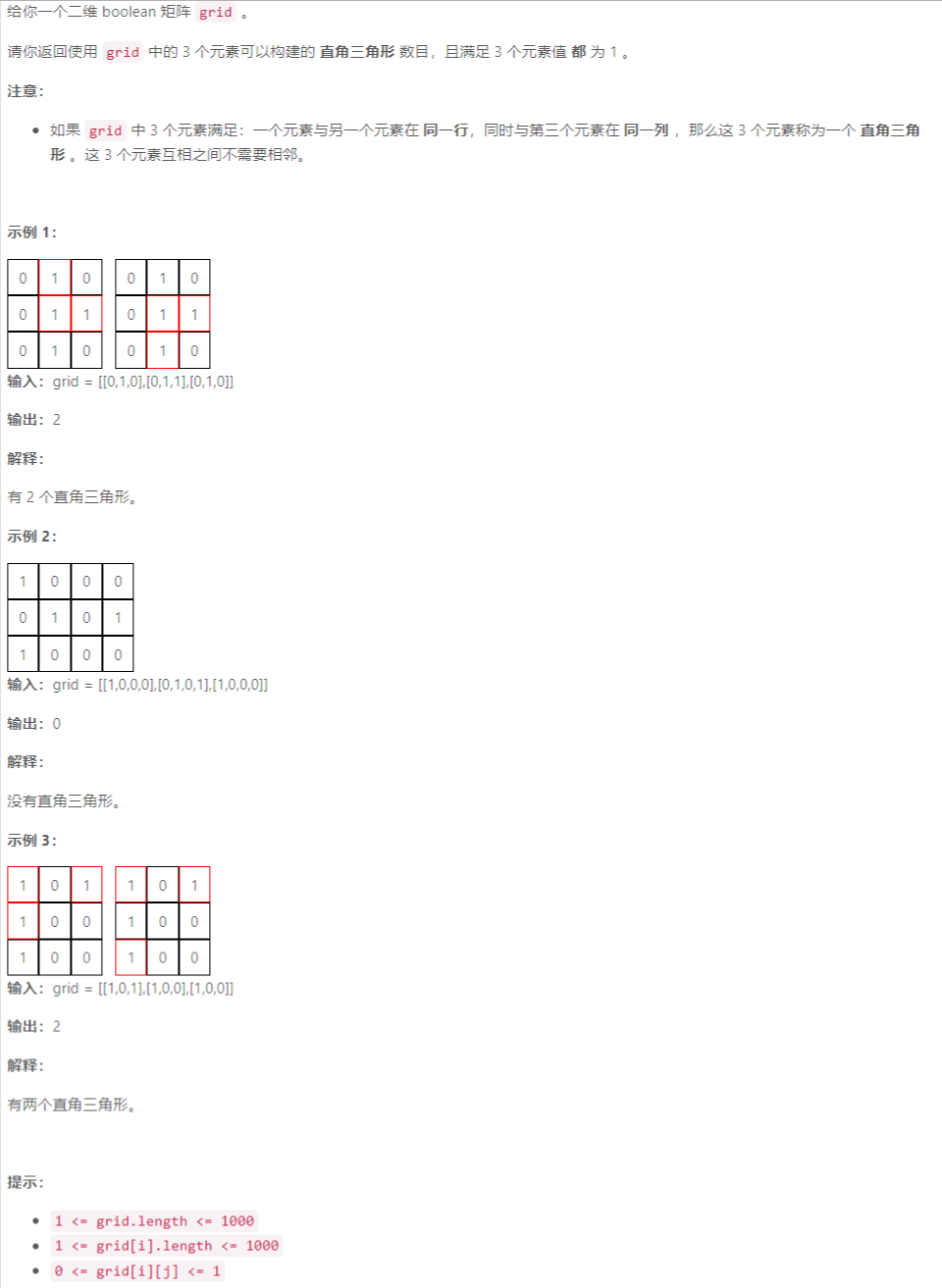
枚举:记录各行各列的 1 1 1 的数目,然后枚举每个直接三角形的直角所在的位置 g r i d [ i ] [ j ] grid[i][j] grid[i][j]
class Solution {public:long long numberOfRightTriangles(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<int> row(m), col(n);for (int i = 0; i < m; i++)for (int j = 0; j < n; j++) {row[i] += grid[i][j];col[j] += grid[i][j];}long long res = 0;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)if (grid[i][j])res += 1LL * (row[i] - 1) * (col[j] - 1);return res;}
};
C 找出所有稳定的二进制数组 I

动态规划:设 p [ i ] [ j ] [ t a i l ] p[i][j][tail] p[i][j][tail] 为含有 i i i 个 0 0 0 和 j j j 个 1 1 1 且以 t a i l tail tail 为结尾的稳定二进制数组的个数,可以枚举其全为 t a i l tail tail 的后缀数组的可能长度来进行状态转移
class Solution {public:using ll = long long;ll mod = 1e9 + 7;int numberOfStableArrays(int zero, int one, int limit) {ll p[zero + 1][one + 1][2]; memset(p, 0, sizeof(p));for (int cz = 1; cz <= zero && cz <= limit; ++cz)p[cz][0][0] = 1;for (int co = 1; co <= one && co <= limit; ++co)p[0][co][1] = 1;for (int i = 0; i <= zero; i++) {for (int j = 0; j <= one; j++) {for (int last = 1; last <= limit; last++) {//全为tail的后缀数组的长度为lastif (i - last >= 0)p[i][j][0] = (p[i][j][0] + p[i - last][j][1]) % mod;if (j - last >= 0)p[i][j][1] = (p[i][j][1] + p[i][j - last][0]) % mod;}}}return ((p[zero][one][0] + p[zero][one][1]) % mod + mod) % mod;}
};
D 找出所有稳定的二进制数组 II

动态规划:设 p [ i ] [ j ] [ t a i l ] p[i][j][tail] p[i][j][tail] 为含有 i i i 个 0 0 0 和 j j j 个 1 1 1 且以 t a i l tail tail 为结尾的稳定二进制数组的个数,枚举其全为 t a i l tail tail 的后缀数组的可能长度来进行状态转移,可以通过维护两个前缀和来优化状态转移的时间复杂度
class Solution {public:using ll = long long;ll mod = 1e9 + 7;int numberOfStableArrays(int zero, int one, int limit) {ll p[zero + 1][one + 1][2]; ll ps0[zero + 1][one + 1];ll ps1[zero + 1][one + 1];memset(p, 0, sizeof(p));memset(ps0, 0, sizeof(ps0));memset(ps1, 0, sizeof(ps1));for (int i = 1; i <= zero && i <= limit; ++i) {p[i][0][0] = 1;ps0[i][0] = 1;}for (int j = 1; j <= one && j <= limit; ++j) {p[0][j][1] = 1;ps1[0][j] = 1;}for (int i = 0; i <= zero; i++) {for (int j = 0; j <= one; j++) {// [max(0,i-limit),i-1]if (int l = max(0, i - limit), r = i - 1; l <= r)p[i][j][0] += l != 0 ? (ps1[r][j] - ps1[l - 1][j]) % mod : ps1[r][j];if (int l = max(0, j - limit), r = j - 1; l <= r)p[i][j][1] += l != 0 ? (ps0[i][r] - ps0[i][l - 1]) % mod : ps0[i][r];if (j)ps0[i][j] = (ps0[i][j - 1] + p[i][j][0]) % mod;if (i)ps1[i][j] = (ps1[i - 1][j] + p[i][j][1]) % mod;}}return ((p[zero][one][0] + p[zero][one][1]) % mod + mod) % mod;}
};
相关文章:

第 129 场 LeetCode 双周赛题解
A 构造相同颜色的正方形 枚举:枚举每个 3 3 3\times 3 33的矩阵,判断是否满足条件 class Solution {public:bool canMakeSquare(vector<vector<char>>& grid) {for (int i 0; i < 2; i)for (int j 0; j < 2; j) {int c1 0, c…...
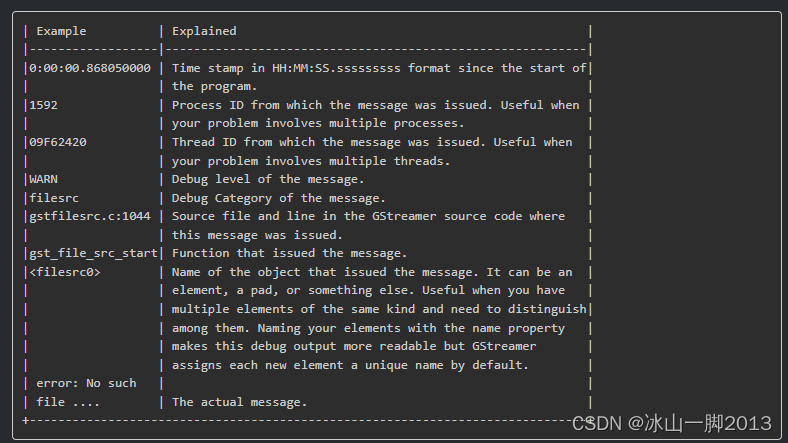
GStreamer日志调试笔记
1、查询所有分类 #gst-launch-1.0 --gst-debug-help 2、查询videotestsrc的日志 #gst-launch-1.0 --gst-debug-help | findstr videotestsrc 结果: 3、使用--gst-debug设置相应日志类型的相应等级,越大显示日志越多,排查内存泄露可以设置为9 …...

【api接口开通教程】YouTube Data API v3申请流程
一、背景调查 1.1 API接口介绍 采集youtube数据,大体分为两种方案:一种是基于爬虫,一种是基于API接口。 说人话就是:爬虫相当于走后门、爬窗户(利用技术手段窃取,人家没说给,但我硬拿&#x…...
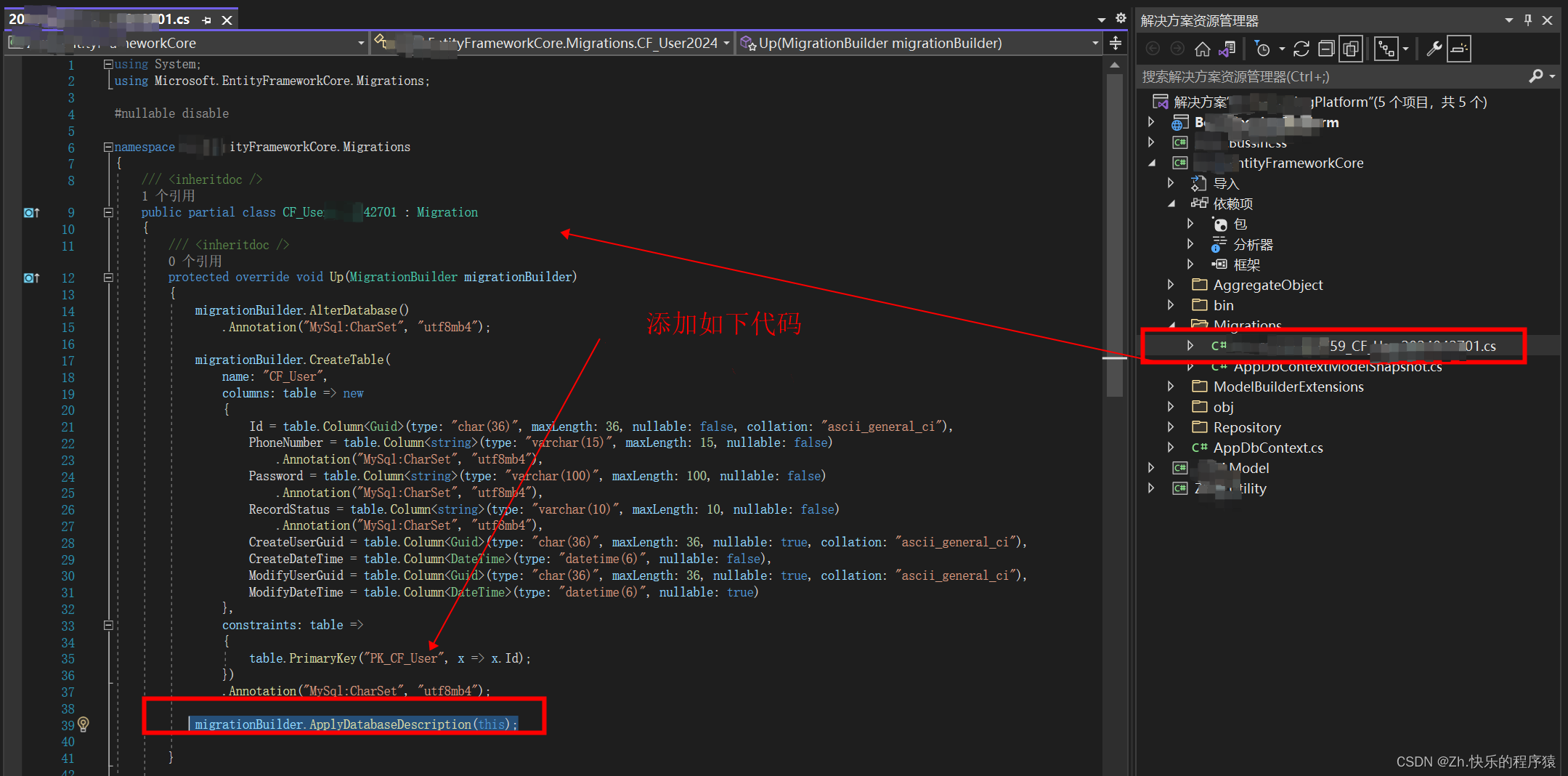
.net 6.0 框架集成ef实战,步骤详解
一、代码框架搭建 搭建如下代码架构: 重点含EntityFrameworkCore工程,该工程中包含AppDbContext.cs和数据表实体AggregateObject 1、AppDbContext 代码案例 //AppDbContext 代码案例using Microsoft.EntityFrameworkCore;namespace EntityFrameworkCo…...

[C/C++] -- 观察者模式
观察者模式是一种行为型设计模式,用于定义对象间的一种一对多的依赖关系,使得当一个对象的状态发生改变时,所有依赖于它的对象都会得到通知并自动更新。 观察者模式涉及以下几个角色: 主题(Subject)&…...

秋招算法刷题8
20240422 2.两数相加 时间复杂度O(max(m,n)),空间复杂度O(1) public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode headnull,tailnull;int carry0;while(l1!null||l2!null){int n1l1!null?l1.val:0;int n2l2!…...

Docker使用方法
Docker是一种容器化平台,它可以帮助开发人员将应用程序和其依赖项打包成一个独立的、可移植的容器,以便在不同的环境中运行。 以下是使用Docker的基本步骤: 安装Docker:首先,您需要在您的机器上安装Docker。您可以从D…...

HTML学习|网页基本信息、网页基本标签、图像标签、超链接标签、列表标签、表格标签、媒体元素、页面结构分析、iframe内联框架
网页基本信息 DOCTYPE是设置使用什么规范,网页整个信息都在html标签中,head标签里包含字符集设置,网页介绍等信息,title标签是网页的名称,网页的主干都在body标签中 网页基本标签 标题标签 h1~h6都是标题标签&#x…...
(消息推送))
001 websocket(评论功能demo)(消息推送)
文章目录 ReviewController.javaWebSocketConfig.javaWebSocketProcess.javaServletInitializer.javaWebsocketApplication.javareadmeindex.htmlapplication.yamlpom.xml ReviewController.java package com.example.controller;import com.example.websocket.WebSocketProces…...
二分查找向下取整导致的死循环69. x 的平方根
二分查找向下取整导致的死循环 考虑伪题目:从数组arr中查找出目标元素target对应的下标,如果数组中不存在目标元素,找 到第一个元素值小于target的元素的下标。 编写二分查找算法如下: Testvoid testBinarySearch(){int[] arr n…...

Kivy 异步任务
如果要进行一些非常耗时的操作(例如:爬虫等),那么页面就会在这里卡住,而系统就会以为这个软件无响应,并提示关闭,可以说明用户体验极差,因此我们在此处引入异步操作。 在py中引入事件调节器,并在…...
))
DEV--C++小游戏(吃星星(0.1))
目录 吃星星(0.1) 简介 头文件 命名空间变量 副函数 清屏函数 打印地图函数 移动函数 主函数 0.1版完整代码 吃星星(0.1) 注:版本<1为未实现或只实现部分 简介 用wasd去吃‘*’ 头文件 #include<bi…...

LINUX 入门 4
LINUX 入门 4 day6 7 20240429 20240504 耗时:240min 课程链接地址 第4章 LINUX环境编程——实现线程池 C基础 第3节 #define里面的行不能乱空行,要换行就打\ typedef 是 C 和 C 中的一个关键字,用于为已有的数据类型定义一个新的名字。…...
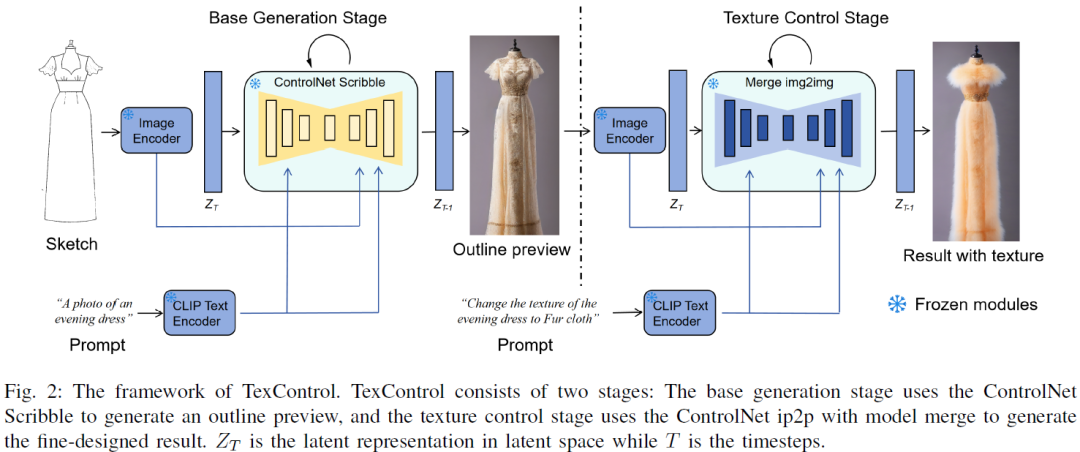
Imagine Flash、StyleMamba 、FlexControl、Multi-Scene T2V、TexControl
本文首发于公众号:机器感知 Imagine Flash、StyleMamba 、FlexControl、Multi-Scene T2V、TexControl You Only Cache Once: Decoder-Decoder Architectures for Language Models We introduce a decoder-decoder architecture, YOCO, for large language models, …...
 方法详解)
Java Collections.emptyList() 方法详解
前言 在Java开发的日常中,我们常常需要处理集合数据结构,而这其中就免不了要面对“空集合”的场景。传统的做法可能是直接返回 null,但这往往会引入空指针异常的风险,降低了代码的健壮性。幸运的是,Java为我们提供了一…...
Vue前端环境准备
vue-cli Vue-cli是Vue官方提供的脚手架,用于快速生成一个Vue项目模板 提供功能: 统一的目录结构 本地调试 热部署 单元测试 集成打包上线 依赖环境:NodeJs 安装NodeJs与Vue-Cli 1、安装nodejs(已经安装就不用了) node-…...

代码随想录算法训练营第四十二天| 01背包问题(二维、一维)、416.分割等和子集
系列文章目录 目录 系列文章目录动态规划:01背包理论基础①二维数组②一维数组(滚动数组) 416. 分割等和子集①回溯法(超时)②动态规划(01背包)未剪枝版剪枝版 动态规划:01背包理论基…...

故障——蓝桥杯十三届2022国赛大学B组真题
问题分析 这道题纯数学,考察贝叶斯公式 AC_Code #include <bits/stdc.h> using namespace std; typedef pair<int,double> PI; bool cmp(PI a,PI b){if(a.second!b.second)return a.second>b.second;return a.first<b.first; } int main() {i…...

SSD存储基本知识
存储技术随着时间的推移经历了显著变化,新兴的存储介质正逐步挑战已经成为行业标准的硬盘驱动器(HDD)。在众多竞争者中,固态硬盘(SSD)是最广泛采用且最有潜力占据主导地位的——它们速度快、运行安静&#…...
buuctf-misc题目练习二
ningen 打开题目后是一张图片,放进winhex里面 发现PK,PK是压缩包ZIP 文件的文件头,下一步是想办法进行分离 Foremost可以依据文件内的文件头和文件尾对一个文件进行分离,或者识别当前的文件是什么文件。比如拓展名被删除、被附加…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...

Unity-ECS详解
今天我们来了解Unity最先进的技术——ECS架构(EntityComponentSystem)。 Unity官方下有源码,我们下载源码后来学习。 ECS 与OOP(Object-Oriented Programming)对应,ECS是一种完全不同的编程范式与数据架构…...
)
python数据结构和算法(1)
数据结构和算法简介 数据结构:存储和组织数据的方式,决定了数据的存储方式和访问方式。 算法:解决问题的思维、步骤和方法。 程序 数据结构 算法 算法 算法的独立性 算法是独立存在的一种解决问题的方法和思想,对于算法而言&a…...
Xcode 16.2 版本 pod init 报错
Xcode 版本升级到 16.2 后,项目执行 pod init 报错; ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchron…...
