【Java 刷题记录】位运算
位运算
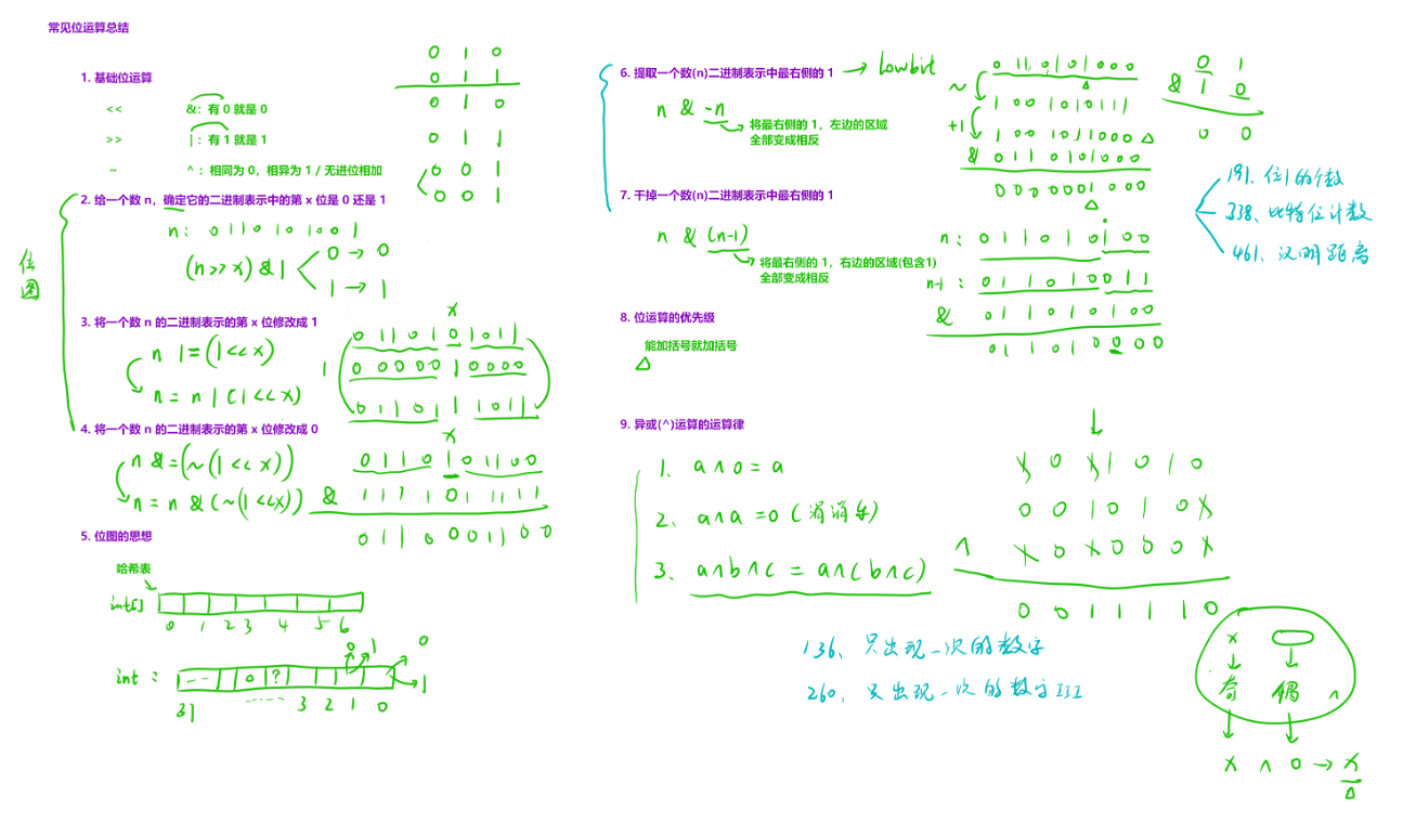
33. 位1的个数
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中
设置位
的个数(也被称为汉明重量)。
示例 1:
输入:n = 11 输出:3 解释:输入的二进制串 1011 中,共有 3 个设置位。示例 2:
输入:n = 128 输出:1 解释:输入的二进制串 10000000 中,共有 1 个设置位。示例 3:
输入:n = 2147483645 输出:30 解释:输入的二进制串 11111111111111111111111111111101 中,共有 30 个设置位。提示:
- 1 <= n <= 231 - 1
进阶:
- 如果多次调用这个函数,你将如何优化你的算法?
class Solution {public int hammingWeight(int n) {int count = 0;while(n != 0) {count++;n &= n - 1;}return count;}
}
34. 比特位计数
给你一个整数
n,对于0 <= i <= n中的每个i,计算其二进制表示中1的个数 ,返回一个长度为n + 1的数组ans作为答案。示例 1:
输入:n = 2 输出:[0,1,1] 解释: 0 --> 0 1 --> 1 2 --> 10示例 2:
输入:n = 5 输出:[0,1,1,2,1,2] 解释: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101提示:
- 0 <= n <= 105
进阶:
- 很容易就能实现时间复杂度为
O(n log n)的解决方案,你可以在线性时间复杂度O(n)内用一趟扫描解决此问题吗?- 你能不使用任何内置函数解决此问题吗?(如,C++ 中的
__builtin_popcount)
class Solution {public int[] countBits(int n) {int[] ret = new int[n + 1];for(int i = 0; i <= n; i++) {ret[i] = ret[i >>> 1] + (i & 1);}return ret;}
}
35. 汉明距离
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数
x和y,计算并返回它们之间的汉明距离。示例 1:
输入:x = 1, y = 4 输出:2 解释: 1 (0 0 0 1) 4 (0 1 0 0)↑ ↑ 上面的箭头指出了对应二进制位不同的位置。示例 2:
输入:x = 3, y = 1 输出:1提示:
- 0 <= x, y <= 231 - 1
class Solution {public int hammingDistance(int x, int y) {int n = x ^ y;int count = 0;while(n != 0) {count++;n &= n - 1;}return count;}
}
36. 只出现一次的数字
给你一个 非空 整数数组
nums,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1] 输出:1示例 2 :
输入:nums = [4,1,2,1,2] 输出:4示例 3 :
输入:nums = [1] 输出:1提示:
- 1 <= nums.length <= 3 * 104
- -3 * 104 <= nums[i] <= 3 * 104
- 除了某个元素只出现一次以外,其余每个元素均出现两次。
class Solution {public int singleNumber(int[] nums) {int n = nums.length;int ret = 0;for(int i = 0; i < n; i++) {ret ^= nums[i];}return ret;}
}
37. 只出现一次的数字 III
给你一个整数数组
nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
示例 1:
输入:nums = [1,2,1,3,2,5] 输出:[3,5] 解释:[5, 3] 也是有效的答案。示例 2:
输入:nums = [-1,0] 输出:[-1,0]示例 3:
输入:nums = [0,1] 输出:[1,0]提示:
- 2 <= nums.length <= 3 * 104
- -231 <= nums[i] <= 231 - 1
- 除两个只出现一次的整数外,
nums中的其他数字都出现两次
class Solution {public int[] singleNumber(int[] nums) {int x = 0;int n = nums.length;for(int i = 0; i < n; i++) {x ^= nums[i];}// 找到一个标志位(可以是任意一个,但是必须是准确的)int flag = x == Integer.MIN_VALUE ? x : x & (-x);// 根据标志位划分两个部分int ret1 = 0;int ret2 = 0;for(int i = 0; i < n; i++) {int number = nums[i];if((number & flag) == 0) {ret1 ^= number;}else {ret2 ^= number;}}return new int[]{ret1, ret2};}
}
38. 判定字符是否唯一
实现一个算法,确定一个字符串
s的所有字符是否全都不同。示例 1:
输入: s = "leetcode" 输出: false示例 2:
输入: s = "abc" 输出: true限制:
0 <= len(s) <= 100s[i]仅包含小写字母- 如果你不使用额外的数据结构,会很加分。
class Solution {public boolean isUnique(String str) {int len = str.length();if(len > 26) return false;int bitMap = 0;for(int i = 0; i < len; i++) {int change = 1 << (str.charAt(i) - 'a');if((change & bitMap) == 0) bitMap |= change;else return false;}return true;}
}
39. 丢失的数字
给定一个包含
[0, n]中n个数的数组nums,找出[0, n]这个范围内没有出现在数组中的那个数。示例 1:
输入:nums = [3,0,1] 输出:2 解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。示例 2:
输入:nums = [0,1] 输出:2 解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1] 输出:8 解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。示例 4:
输入:nums = [0] 输出:1 解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。提示:
n == nums.length- 1 <= n <= 104
0 <= nums[i] <= nnums中的所有数字都 独一无二
class Solution {public int missingNumber(int[] nums) {int ret = 0;int n = nums.length;for(int i = 0; i < n; i++) {ret ^= i ^ nums[i];}return ret ^ n;}
}
40. 两整数之和
给你两个整数
a和b,不使用 运算符+和-,计算并返回两整数之和。示例 1:
输入:a = 1, b = 2 输出:3示例 2:
输入:a = 2, b = 3 输出:5提示:
-1000 <= a, b <= 1000
class Solution {public int getSum(int a, int b) {while(b != 0) {int tmp = a;a ^= b; // 无进位相加b = (tmp & b) << 1; // 进位 carry}return a;}
}
41. 只出现一次的数字 II
给你一个整数数组
nums,除某个元素仅出现 一次 外,其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2] 输出:3示例 2:
输入:nums = [0,1,0,1,0,1,99] 输出:99提示:
- 1 <= nums.length <= 3 * 104
- -231 <= nums[i] <= 231 - 1
nums中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
class Solution {public int singleNumber(int[] nums) {int ret = 0;for(int i = 0; i < 32; i++) {int sum = 0;for(int num : nums) {sum += (num >>> i) & 1;}ret |= (sum % 3) << i;}return ret;}
}
42. 消失的两个数字
给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗?
以任意顺序返回这两个数字均可。
示例 1:
输入: [1] 输出: [2,3]示例 2:
输入: [2,3] 输出: [1,4]提示:
nums.length <= 30000
class Solution {public int[] missingTwo(int[] nums) {int x = 0;int n = nums.length;for(int num : nums) {x ^= num;}for(int i = 1; i <= n + 2; i++) {x ^= i;}int flag = x == Integer.MIN_VALUE ? x : (x & (-x));int lose1= 0;int lose2 = 0;for(int num : nums) {if((num & flag) == 0) lose1 ^= num;else lose2 ^= num;}for(int i = 1; i <= n + 2; i++) {if((i & flag) == 0) lose1 ^= i;else lose2 ^= i;}return new int[]{lose1, lose2};}
}
相关文章:

【Java 刷题记录】位运算
位运算 33. 位1的个数 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中 设置位 的个数(也被称为汉明重量)。 示例 1: 输入:n 11 输出:3 解释…...
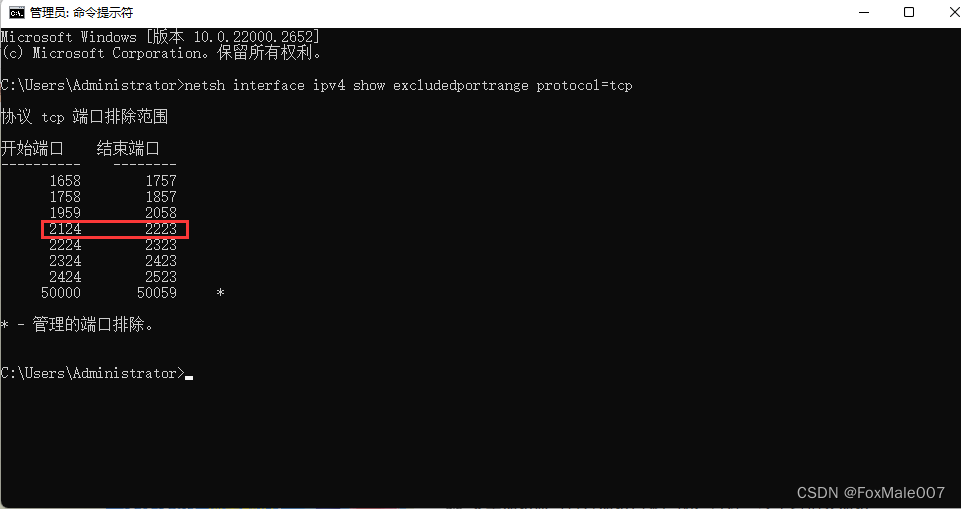
WINDOWS下zookeeper突然无法启动但是端口未占用的解决办法(用了WSL)
windows下用着用着时候突然zookeeper启动不了了。netstat查也没有找到端口占用,就是起不来。控制台报错 java.lang.reflect.UndeclaredThrowableException: nullat org.springframework.util.ReflectionUtils.rethrowRuntimeException(ReflectionUtils.java:147) ~…...

【LLM第三篇】名词解释:RLHF——chatgpt的功臣
RLHF (Reinforcement Learning from Human Feedback) ,直译为:“来自人类反馈的强化学习”。RLHF是一种结合了强化学习和人类反馈的机器学习方法,主要用于训练大模型以执行复杂的任务,尤其是当这些任务难以通过传统的奖励函数来精…...
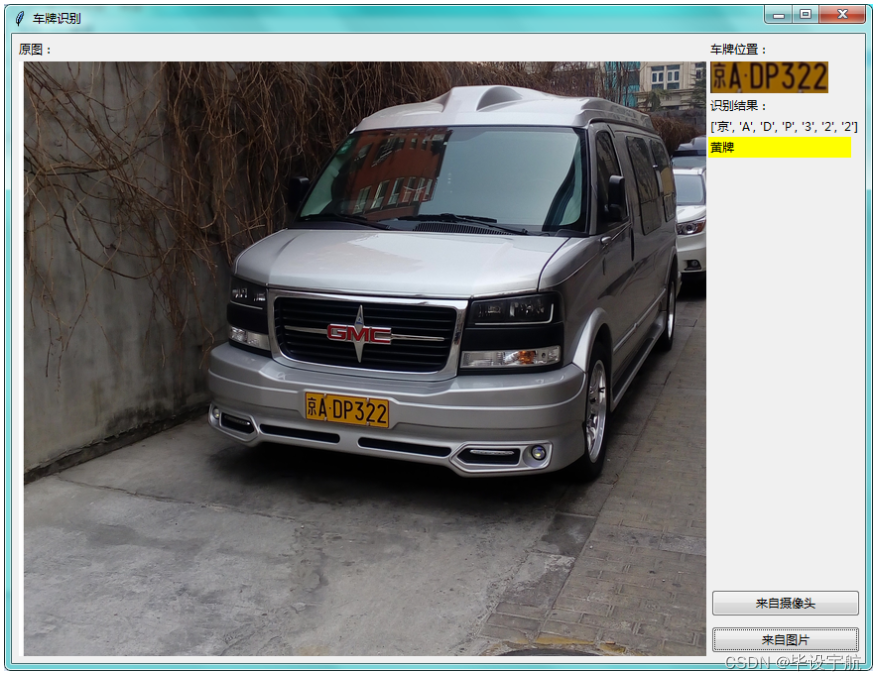
基于Opencv的车牌识别系统(毕业设计可用)
系统架构 图像采集:首先,通过摄像头等设备捕捉车辆图像。图像质量直接影响后续处理的准确性,因此高质量的图像采集是基础。 预处理:对获取的原始图像进行预处理,包括灰度化、降噪、对比度增强和边缘检测等。这些操作旨…...

Leetcode—295. 数据流的中位数【困难】
2024每日刷题(132) Leetcode—295. 数据流的中位数 实现代码 class MedianFinder { public:MedianFinder() {}void addNum(int num) {if(maxHeap.empty() || num < maxHeap.top()) {maxHeap.push(num);} else {minHeap.push(num);}if(maxHeap.size(…...

JavaWeb之过滤器(Filter)与监听器(Listener)
前言 过滤器(Filter) 1.什么是过滤器 2.过滤器的语法格式 3.使用场景 3.1.如何防止用户未登录就执行后续操作 3.2.设置编码方式--统一设置编码 3.3.加密解密(密码的加密和解密) 3.4.非法文字筛选 3.5.下载资源的限制 监听器(Listener) 1.什么是监听器 2.监听器分类…...

video.js的请求头问题
为了防止视频被轻易下载,我们项目需要在请求视频地址的时候,增加token识别,避免url一粘贴到浏览器地址上就能被盗。 明明一开始就找到的方法: // ts-ignorevideojs.Vhs.xhr.beforeRequest function (options) {options.headers …...

leetcode 1235
leetcode 1235 代码 class Solution { public:int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {int n startTime.size();vector<vector<int>> jobs(n);for(int i0; i<n; i){jobs[i] …...
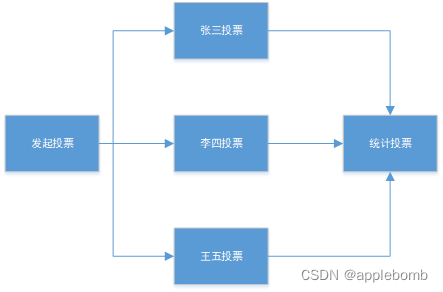
Activiti7 开发快速入门【2024版】
记录开发最核心的部分,理论结合业务实操减少废话,从未接触工作流快速带入开发。假设你是后端的同学学过JAVA和流程图,则可以继续向后看,否则先把基础课程书准备好先翻翻。 为什么要工作流 比起直接使用状态字段,工作…...
vue3组件插槽
Index.vue: <script setup> import { ref, onMounted } from vue import Child from ./Child.vue import ./index.cssonMounted(() > {}) </script><template><div class"m-home-wrap"><Child>插槽</Child><div class&qu…...

Cloudera简介和安装部署
ChatGPT Cloudera 是一个基于 Apache Hadoop 的数据管理和分析平台。它是由 Hadoop 的几位创始人及早期贡献者于 2008 年创立的公司,并随着公司的不断发展,Cloudera 开始提供企业级的解决方案,帮助企业更好地利用 Hadoop 生态系统进行大数据…...
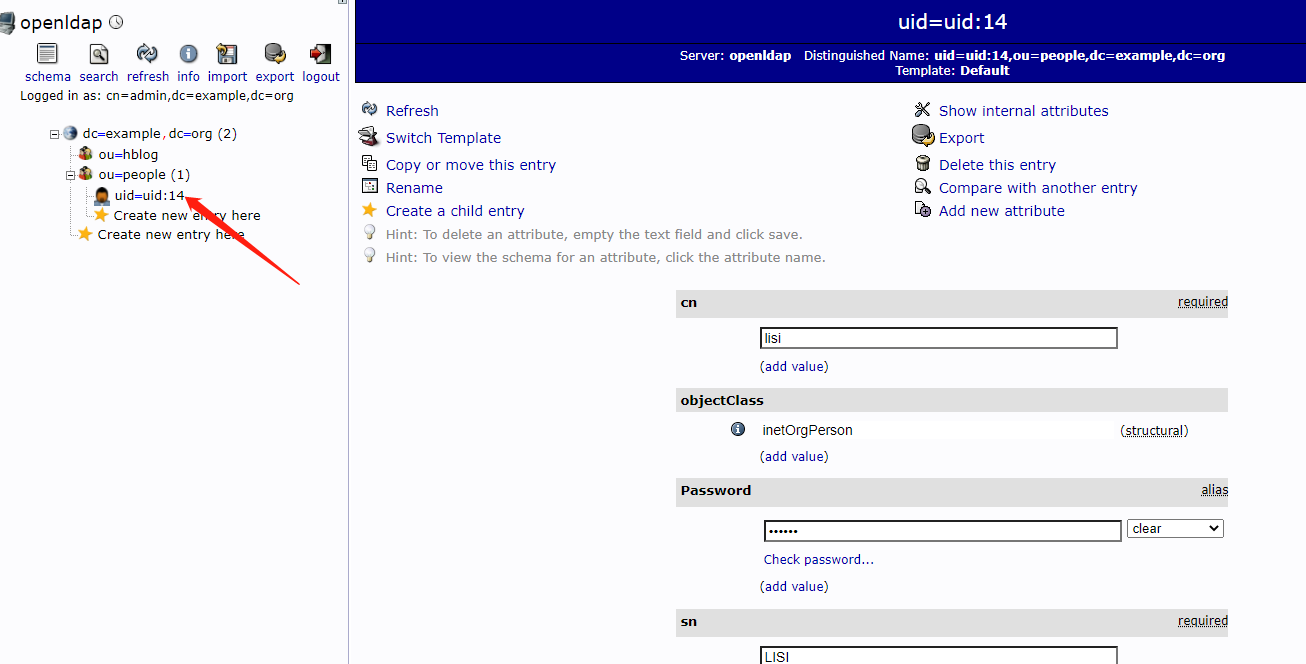
Spring Boot集成Ldap快速入门Demo
1.Ldap介绍 LDAP,Lightweight Directory Access Protocol,轻量级目录访问协议. LDAP是一种特殊的服务器,可以存储数据数据的存储是目录形式的,或者可以理解为树状结构(一层套一层)一般存储关于用户、用户…...
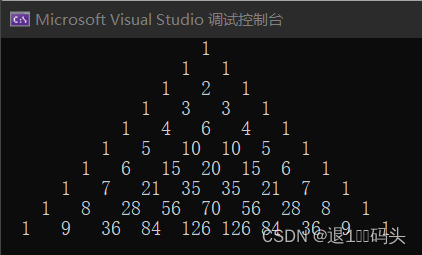
杨辉三角的打印
题目内容: 在屏幕上打印杨辉三角。 思路: 首先我们通过观察发现,每一步的打印都与行列数有关,中间的数据由这一列和上一行的前一列数据控制。所以我们可以使用二维数组进行操作: (1ÿ…...
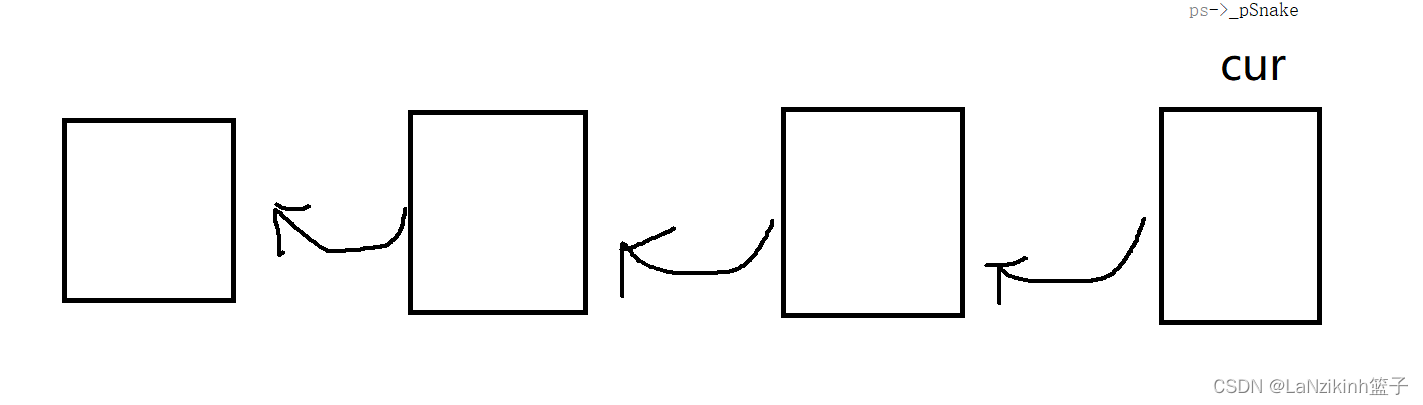
贪吃蛇(下)游戏的实现
感谢大佬的光临各位,希望和大家一起进步,望得到你的三连,互三支持,一起进步 个人主页:LaNzikinh-CSDN博客 文章目录 前言一.蛇和食物的打印二.游戏的运行逻辑三.结束游戏 (善后工作)四.游戏的测…...
偏微分方程算法之椭圆型方程差分格式编程示例
目录 一、示例1-五点菱形格式 1.1 C代码 1.2 计算结果 二、示例2-九点紧差分格式 2.1 C代码 2.2 计算结果 三、示例3-二阶混合边值 3.1 C代码 3.2 计算结果 本专栏对椭圆型偏微分方程的三种主要差分方法进行了介绍,并给出相应格式的理论推导过程。为加深对…...

PCIe协议之-TLP路由基础
✨前言: 在PCI Express (PCIe) 技术中,数据包的路由方式对于确保信息能够高效、准确地传送至目标设备至关重要。PCIe定义了几种路由方式,主要有以下几种。 🌟地址路由(Address Based Routing) 这是最基本…...
可以是内联函数(inline)吗?)
inline内联函数-虚函数(virtual)可以是内联函数(inline)吗?
目录标题 inline内联函数特征:使用:编译器对inline函数的处理步骤优点:缺点: 虚函数(virtual)可以是内联函数(inline)吗?特征:使用: inline内联函…...

Spring Boot | Spring Boot 消息管理 ( 消息中间件 ) 、RabbitMQ“消息中间件“
目录: 一、"消息服务" 概述 :1.1 为什么要使用 "消息服务" ( 消息中间件 ) ?① 异步处理② 应用解耦③ 流量削峰④ 分布式事务管理 1.2 常用 "消息中间件" 介绍 :ActiveMQ ( 广泛应用于中小型企业 )RabbitMQ ( 没有特别要求的场景下…...
二层交换机与路由器连通上网实验
华为二层交换机与路由器连通上网实验 二层交换机是一种网络设备,用于在局域网(LAN)中转发数据帧。它工作在OSI模型的第二层,即数据链路层。二层交换机通过学习和维护MAC地址表,实现了数据的快速转发和广播域的隔离。 实…...

AJAX知识点(前后端交互技术)
原生AJAX AJAX全称为Asynchronous JavaScript And XML,就是异步的JS和XML,通过AJAX可以在浏览器中向服务器发送异步请求,最大的优势:无需刷新就可获取数据。 AJAX不是新的编程语言,而是一种将现有的标准组合在一起使用的新方式 …...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
