【线性代数】俗说矩阵听课笔记
基础解系的概念
线性方程组的解
21行列式和矩阵秩Rank的等价刻画
子式
标准型
利用子式求解矩阵的rank
24零积秩不等式
齐次线性方程组的基础解系
rank的两个重要结论
￥25伴随矩阵的rank
奇异矩阵：行列式=0的矩阵
31线性相关，线性无关，拓展与证明
n个m维向量在n<=m时可能线性相关也可能线性无关，线性无关时可以构成某个m维空间的一组基。m不小于n时，秩小于n则线性相关。
n个m维向量在n>m时可一定线性相关。低维向量一定无法构成高维度空间的一组基。
￥
32极大线性无关组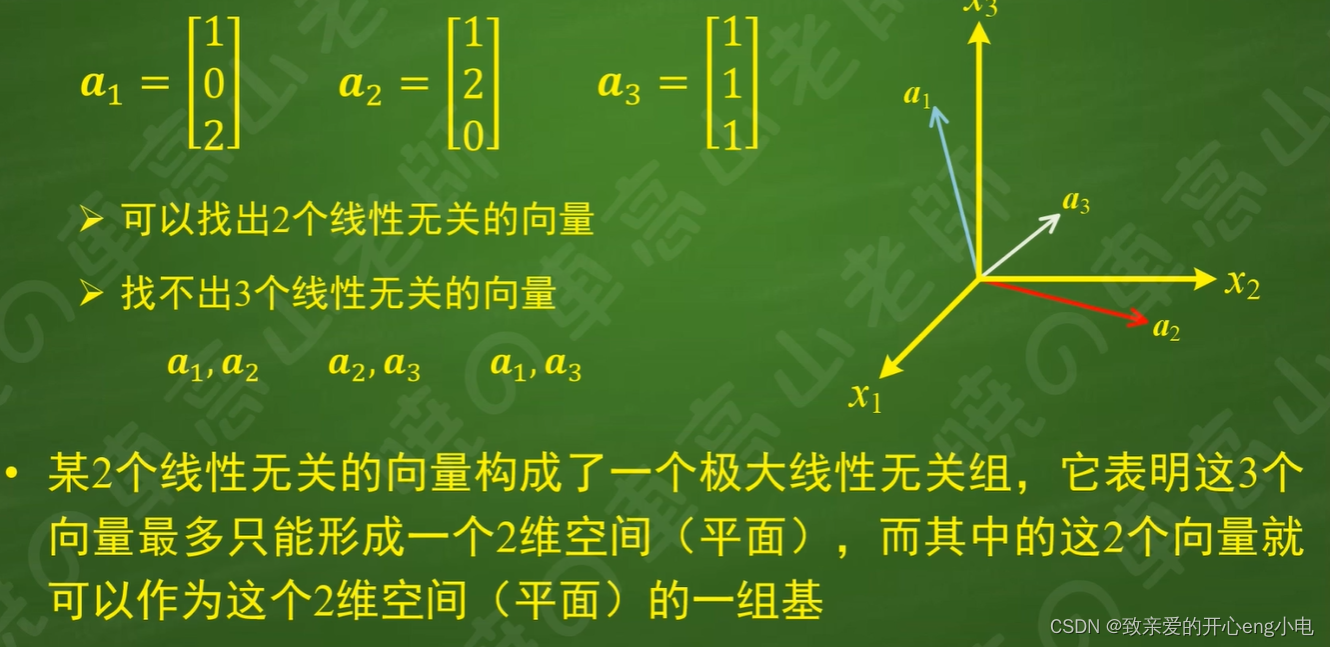
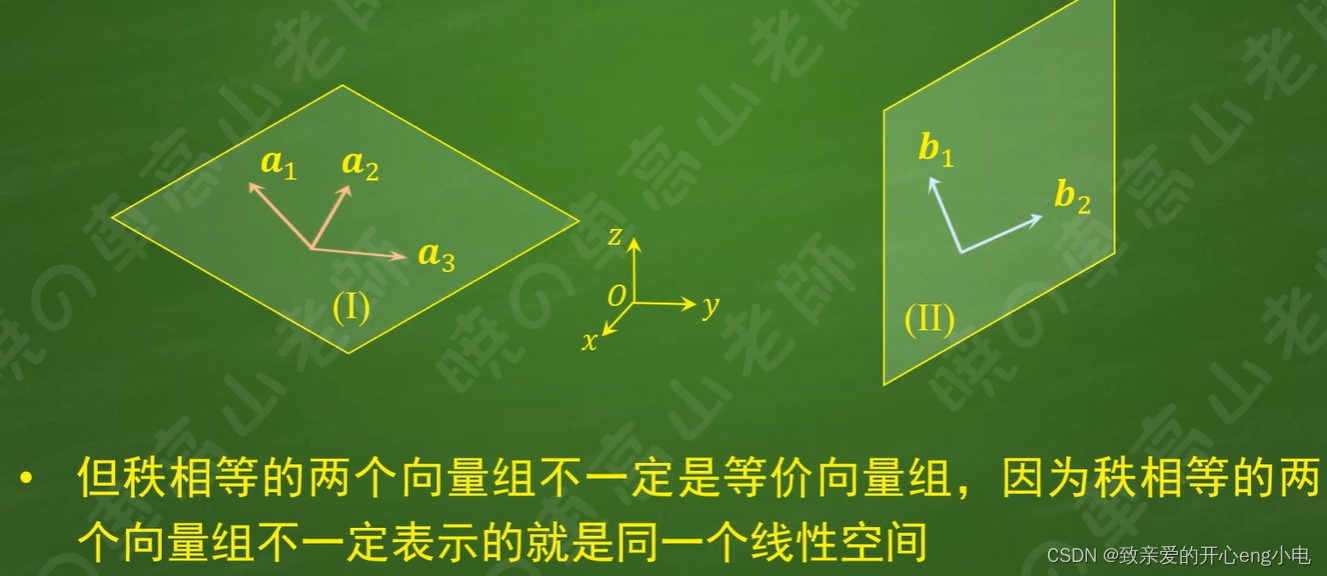
33向量组的等价
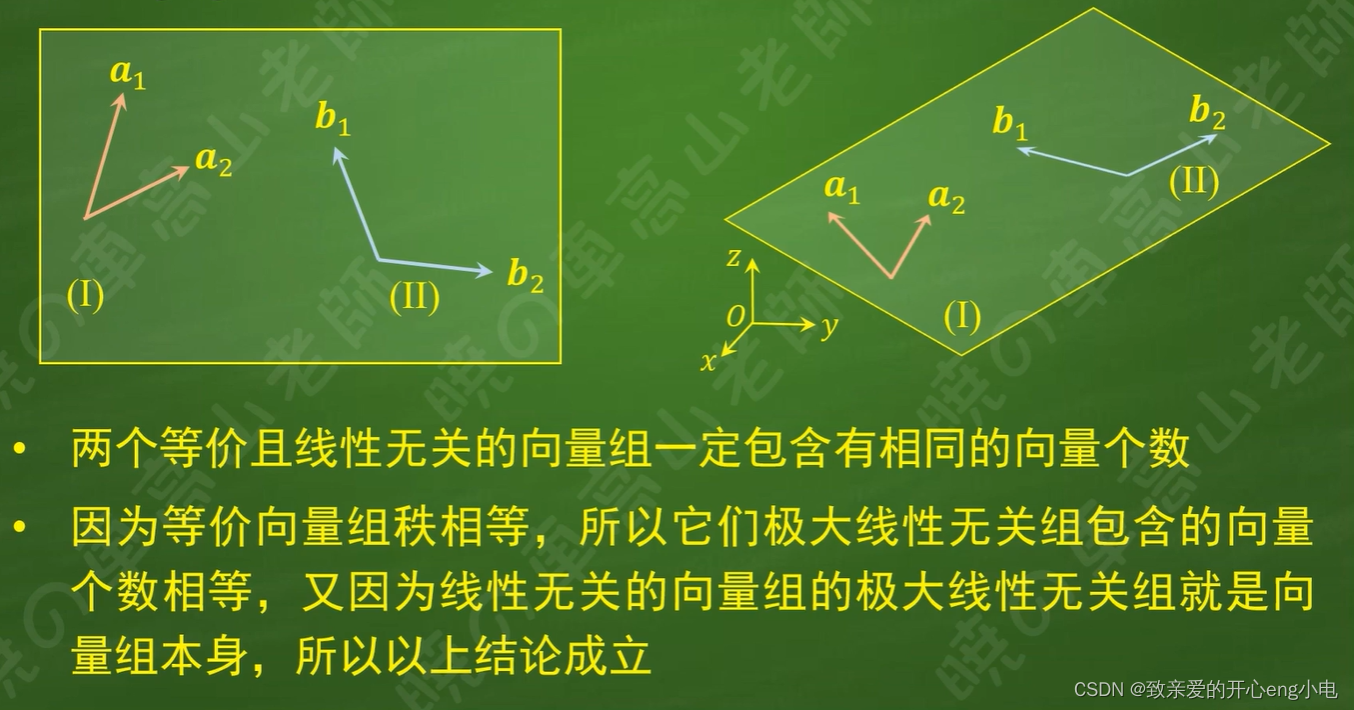
34线性空间基变换
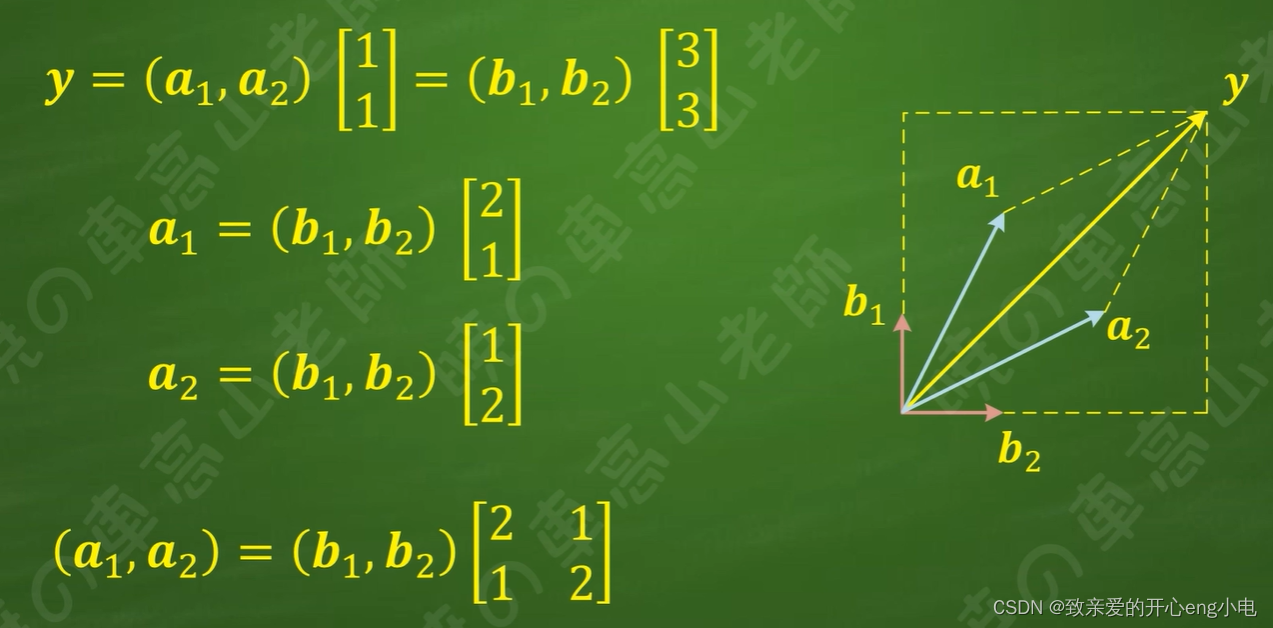
待研究的内容：
1线性无关向量的正交化
2矩阵的特征值和特征向量
3相似矩阵和相似对角化
4二次型及标准二次型
￥35单位正交基向量
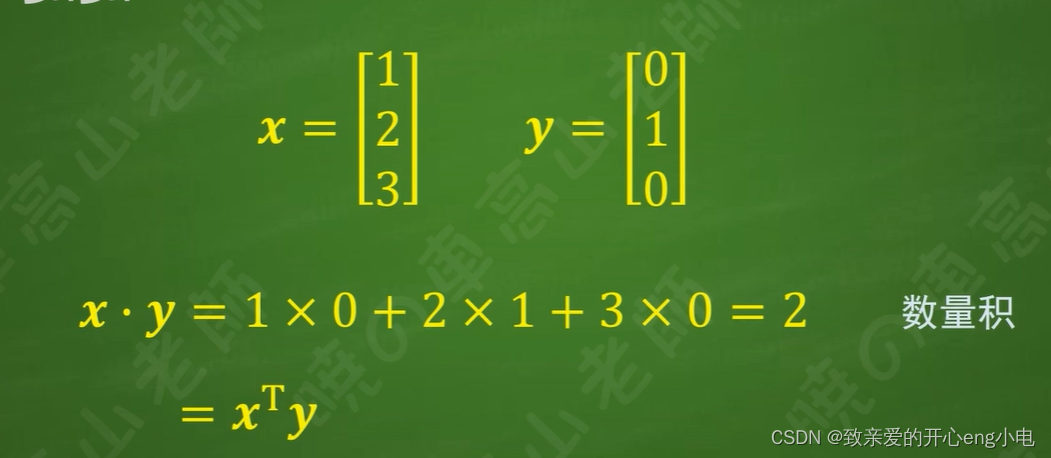两个向量的数量积等于0，则称两者正交或者垂直
研究它的原因：正交基向量，单位正交基向量有非常良好的性质
36斯密特正交化
37特征值和特征向量
概念篇
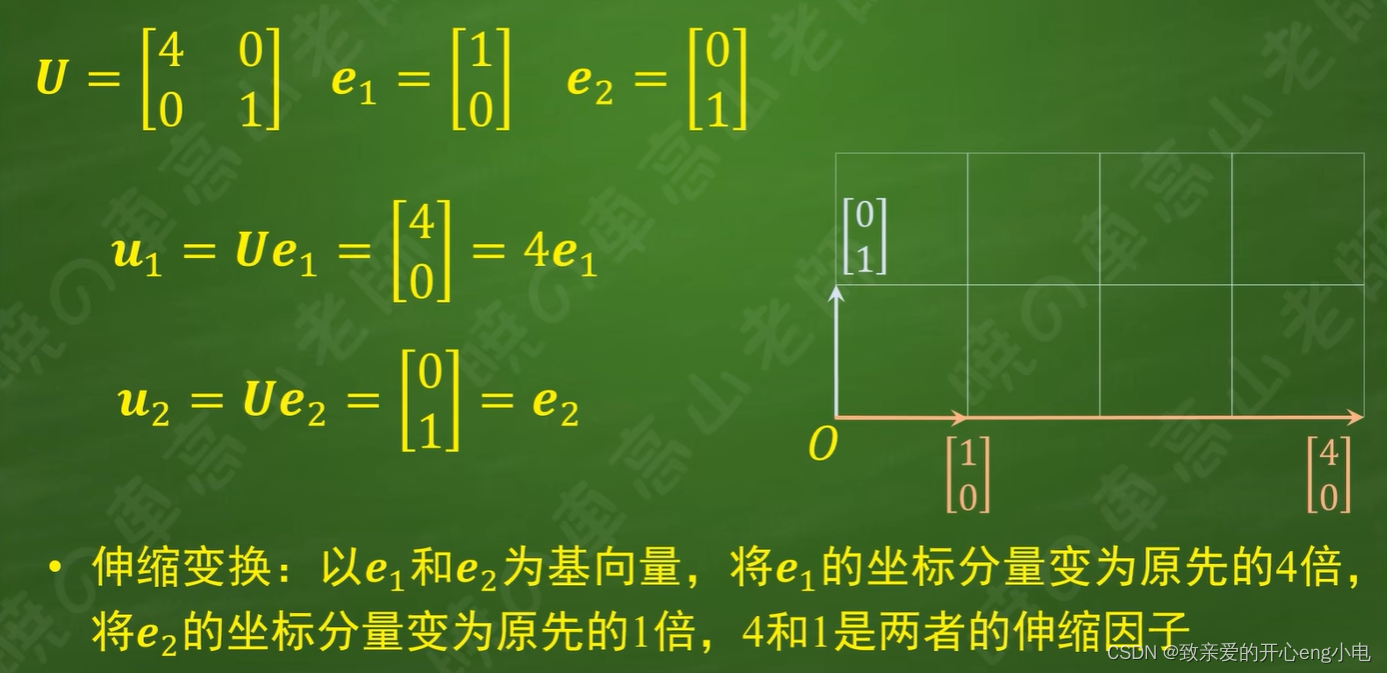
计算篇
性质篇
引用篇
39特征值和特征向量的性质
40特征值和特征向量的计算例题
求特征值和特征向量的步骤
特征值和特征向量的关系
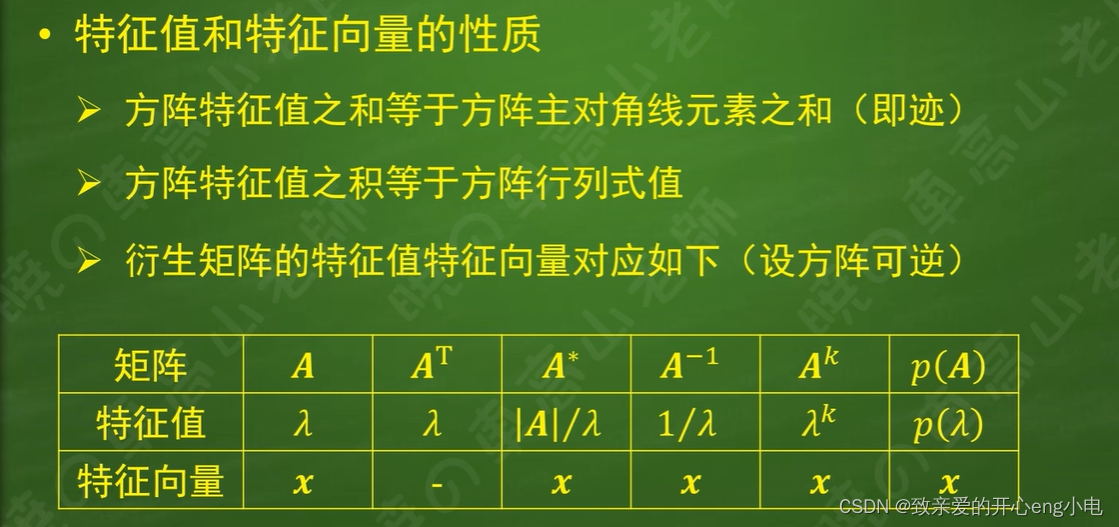
特征值和特征向量的性质
【补充】linear algebra and its applicationsCH4 vector spaces
4.1vector spaces and subspaces
4.2null spaces,column spaces, and linear transformation
4.3linear independent set:bases
4.4coordinate systems
4.5the dimension of a vector space
4.6rank
4.7change of basis
4.8applications to different equations
4.9applications to markov chains
41相似矩阵
相关文章：
【线性代数】俗说矩阵听课笔记
基础解系的概念 线性方程组的解 21行列式和矩阵秩Rank的等价刻画 子式 标准型 利用子式求解矩阵的rank 24零积秩不等式 齐次线性方程组的基础解系 rank的两个重要结论 ￥25伴随矩阵的rank 奇异矩阵：行列式0的矩阵 31线性相关，线性无关&#…...
物联网技术在数字化工厂中的应用，你知道多少？——青创智通
工业物联网解决方案-工业IOT-青创智通 物联网（IoT）技术在数字化工厂的应用正日益成为工业革命的重要推动力。随着科技的飞速发展，物联网技术不断革新，其在数字化工厂中的应用也呈现出愈发广泛和深入的态势。本文将详细探讨物联网…...
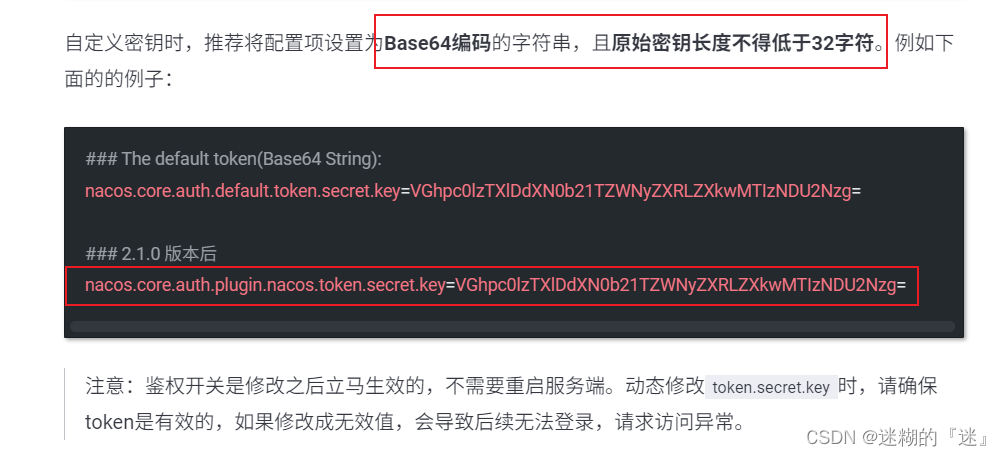
nacos开启登录开关启动报错“Unable to start embedded Tomcat”
nacos 版本：2.3.2 2.2.2版本之前的Nacos默认控制台，无论服务端是否开启鉴权，都会存在一个登录页；在之后的版本关闭了默认登录页面，无需登录直接进入控制台操作。在这里我们可以在官网可以看到相关介绍 而我现在所用的…...
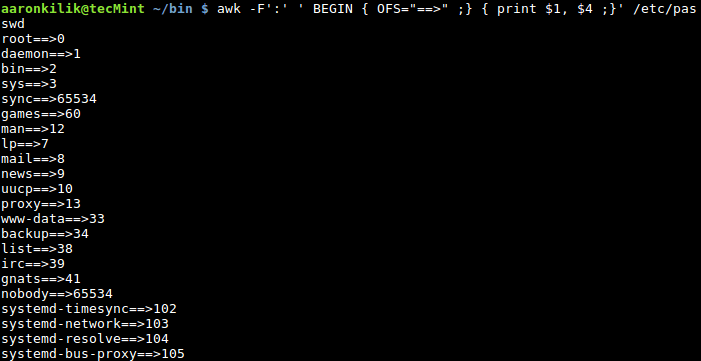
Linux｜了解如何使用 awk 内置变量
引言 当我们揭开 Awk 功能部分时，我们将介绍 Awk 中内置变量的概念。您可以在 Awk 中使用两种类型的变量：用户定义的变量和内置变量。 内置变量的值已经在 Awk 中定义，但我们也可以仔细更改这些值，内置变量包括： FILEN…...
代码随想录-算法训练营day29【回溯算法05：递增子序列、全排列】
代码随想录-035期-算法训练营【博客笔记汇总表】-CSDN博客 第七章 回溯算法part05* 491.递增子序列 * 46.全排列 * 47.全排列 II详细布置 491.递增子序列 本题和大家刚做过的 90.子集II 非常像，但又很不一样，很容易掉坑里。 https://programmercarl.com…...
704. 二分查找
Problem: 704. 二分查找 🐷我的leetcode主页 文章目录 题目分类思路什么是二分查找如何理解时间复杂度 解题方法Code 题目 给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target&a…...
php回车变br、php显示br
在 PHP 中，如果你想将回车符（\n）转换为 HTML 的 <br> 标签来实现换行显示，可以使用内置函数 nl2br()。这个函数会将文本中的换行符替换为 <br> 标签。以下是使用 nl2br() 函数的示例代码： <?php $tex…...
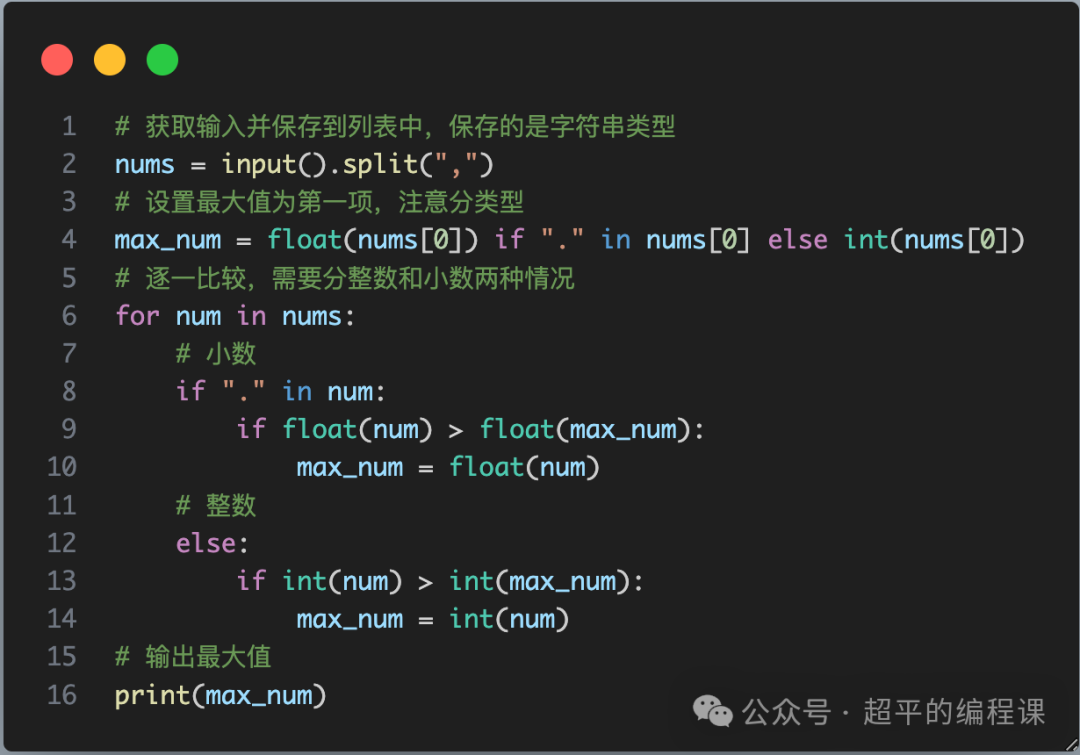
找最大数字-第12届蓝桥杯国赛Python真题解析
[导读]：超平老师的Scratch蓝桥杯真题解读系列在推出之后，受到了广大老师和家长的好评，非常感谢各位的认可和厚爱。作为回馈，超平老师计划推出《Python蓝桥杯真题解析100讲》，这是解读系列的第60讲。 找最大数字&#…...
蓝桥杯 算法提高 ADV-1170 阶乘测试 python AC
找规律题，遍历i中有几个m就加几，和m的多少次数有关 第一版👇 try:while True:n, m map(int, input().split())ll [i for i in range(1, n 1) if i % m 0]ans len(ll)M mwhile ll:lll []M * mfor i in ll:if i % M 0:lll.append(i)a…...
阿里巴巴杭州全球总部正式启用，创新“减碳大脑”科技减碳 | 最新快讯
来源：封面新闻 封面新闻记者付文超 5 月 10 日，记者获悉，位于未来科技城的阿里巴巴杭州全球总部新园区正式启用，这是阿里巴巴目前最大的综合性办公园区。从空中俯瞰，园区正中央呈现阿里标志性的笑脸 logo，这…...
)
蓝桥杯国赛练习题真题Java(矩阵计数)
题目描述 一个 NM 的方格矩阵，每一个方格中包含一个字符 O 或者字符 X。 要求矩阵中不存在连续一行 3 个 X 或者连续一列 3 个 X。 问这样的矩阵一共有多少种？ 输入描述 输入一行包含两个整数 N,M (1≤N,M≤5)。 输出描述 输出一个整数代表答案。…...
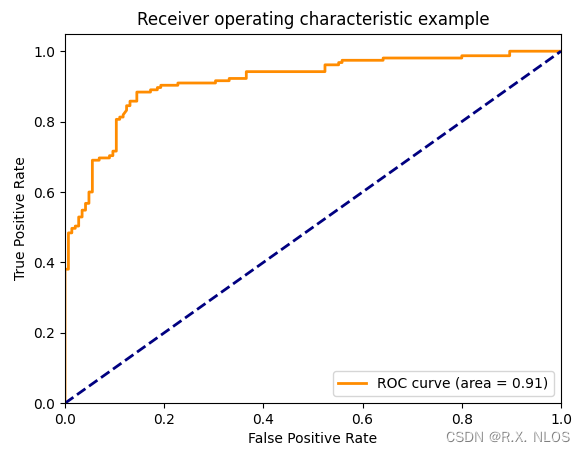
概念解析 | ROC曲线：评估分类模型
注1：本文系"概念解析"系列之一，致力于简洁清晰地解释、辨析复杂而专业的概念。本次辨析的概念是：ROC曲线的含义和绘制 概念解析 | ROC曲线：评估分类模型 第一部分：通俗解释 在我们的日常生活中，经常会遇到需要做出判断和选择的情况。比如，当你收到一封邮件时…...
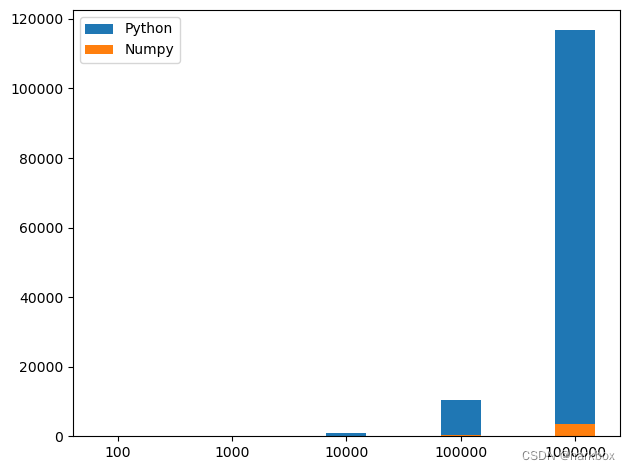
数据可视化训练第二天（对比Python与numpy中的ndarray的效率并且可视化表示)
绪论 千里之行始于足下；继续坚持 1.对比Python和numpy的性能 使用魔法指令%timeit进行对比 需求： 实现两个数组的加法数组 A 是 0 到 N-1 数字的平方数组 B 是 0 到 N-1 数字的立方 import numpy as np def numpy_sum(text_num):"""…...
【Java EE】数据库连接池详解
文章目录 🎍数据库连接池🌸Hikari🌸Druid 🍀MySQL开发企业规范⭕总结 🎍数据库连接池 在上⾯Mybatis的讲解中,我们使⽤了数据库连接池技术,避免频繁的创建连接,销毁连接 下⾯我们来了解下数据库连接池 数据库连接池负…...
正点原子[第二期]Linux之ARM（MX6U）裸机篇学习笔记-15.4讲 GPIO中断实验-IRQ中断服务函数详解
前言： 本文是根据哔哩哔哩网站上“正点原子[第二期]Linux之ARM（MX6U）裸机篇”视频的学习笔记，在这里会记录下正点原子 I.MX6ULL 开发板的配套视频教程所作的实验和学习笔记内容。本文大量引用了正点原子教学视频和链接中的内容。…...
如何平衡RPA机器人的安全性与业务敏捷性，同时不牺牲用户体验？
平衡RPA机器人的安全性与业务敏捷性，同时不牺牲用户体验，是RPA实施中的一个关键挑战。以下是一些策略和最佳实践： ### 1. 安全设计原则 从设计阶段就将安全性纳入考虑，遵循安全设计原则。这意味着在开发RPA解决方案时࿰…...
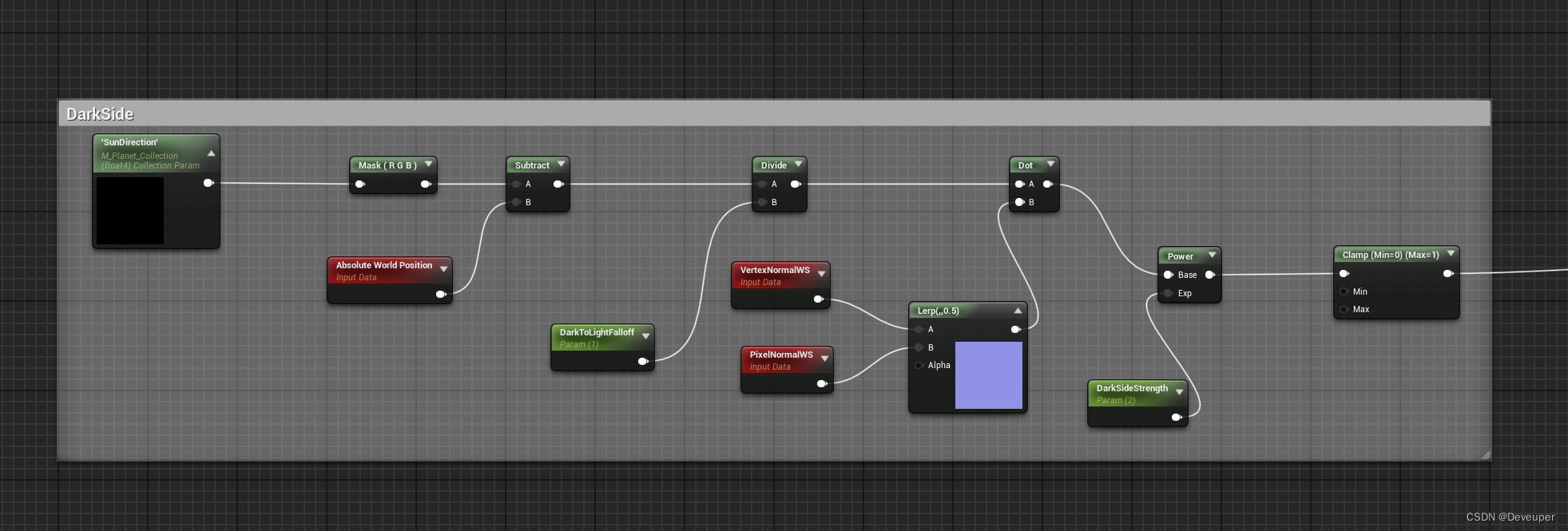
地球行星UE5和UE4
地球行星，包含多种地球风格，可蓝图控制自转和停止，可材质自转. 支持版本4.21-5.4版本 下载位置：https://mbd.pub/o/bread/ZpWZm5lv b站工坊：https://gf.bilibili.com/item/detail/1105582041 _______________________…...
7.k8s中的名称空间namespace
目录 一、Namespace(命名空间) 二、查看系统的名称空间 1.查看系统中的名称空间列表 2.单独查看一个名称空间下的对应资源 三、名称空间的管理 1.创建名称空间 1.1响应式创建 1.2声明式创建 2.删除名称空间 四、资源引用名称空间 一、Namespace(命名空间) 命名空间(Name…...
上海企业源代码防泄密解决方案，企业源代码防泄密如何应对？
随之互联网的发展，企业员工因离职把企业源代码泄露或删库跑路的事情屡见不鲜，各大互联网公司基本都会出现源代码泄露的事情，这样的问题也成了企业在发展过程中不可避免的问题。企业源代码泄露会给企业带来的损失也是不可估量的，据…...
将要上市的自动驾驶新书《自动驾驶系统开发》中摘录各章片段 4
第十三章 车联网 数字化设备正变得越来越普遍并且相互联系。这些设备向数字生态系统智能部分的演进创造了迄今为止尚未解决安全问题的新颖应用。一个特定的例子是车辆，随着车辆从简单的交通方式发展到具有新的感知和通讯功能的智能实体，就成为智能城市的…...
vscode里如何用git
打开vs终端执行如下： 1 初始化 Git 仓库（如果尚未初始化） git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
智慧医疗能源事业线深度画像分析（上）
引言 医疗行业作为现代社会的关键基础设施，其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入，智慧医疗能源事业线应运而生，致力于通过创新技术与管理方案，重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
基于ASP.NET+ SQL Server实现（Web）医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上，开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识，在 vs 2017 平台上，进行 ASP.NET 应用程序和简易网站的开发；初步熟悉开发一…...
FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下，无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作，还是游戏直播的画面实时传输，低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架，凭借其灵活的编解码、数据…...
渗透实战PortSwigger靶场-XSS Lab 14：大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet： https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...
（二）原型模式
原型的功能是将一个已经存在的对象作为源目标，其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现，忽略对象创建过程中的其它细节。 📌 核心特点： 避免重复初…...
Neo4j 集群管理：原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档，本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石，用于构建高可用、可扩展且一致的图数据库服务…...
现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学（ECC）是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础，例如椭圆曲线数字签…...
CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库，而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例，演示如何： 使用 FetchContent 从 GitH…...
使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...