centos安装paddlespeech各种报错解决方案
背景
windows系统安装paddlespeech一路顺利
centos安装之前也是正常
今天centos再次安装各种报错,避免以后遇到浪费时间,记录下来,也给大家节约时间
报错
报错1
module 'numpy' has no attribute 'complex'.
解决方案
降低numpy
# 1. 卸载当前numpy库
pip uninstall numpy
# 2. 较老的NumPy版本
pip install numpy==1.21.6 -i https://pypi.tuna.tsinghua.edu.cn/simple
报错2: distutils.errors.DistutilsError: Command '['/opt/anaconda3/envs/paddlespeech/bin/python', '-m', 'pip', '--disable-pip-version-check', 'wheel', '--no-deps', '-w', '/tmp/tmp_aaw5kbf', '--quiet', '--index-url', 'http://mirrors.tencentyun.com/pypi/simple', 'setuptools_scm']'
解决方案
信任腾讯域名
如果报其它域名,请信任其它域名
pip install paddlespeech --trusted-host mirrors.tencentyun.com 报错3
无法安装setuptools_scm
解决方案
直接手动安装
pip install setuptools_scm报错4
/lib64/libstdc++.so.6: version `GLIBCXX_3.4.29' not found (
解决方案
参考链接:已解决Error:AttributeError: module ‘numpy‘ has no attribute ‘complex‘_attributeerror: module 'numpy' has no attribute 'c-CSDN博客
相关文章:

centos安装paddlespeech各种报错解决方案
背景 windows系统安装paddlespeech一路顺利 centos安装之前也是正常 今天centos再次安装各种报错,避免以后遇到浪费时间,记录下来,也给大家节约时间 报错 报错1 module numpy has no attribute complex. 解决方案 降低numpy # 1. 卸载当前numpy库 pip uninstall numpy…...

谈基于ATTCK框架的攻击链溯源
引言 网络安全在当今数字化时代变得尤为关键,而MITRE公司开发的ATT&CK框架则成为了安全专业人员的重要工具。ATT&CK是一种广泛使用的攻击行为分类和描述框架。其目的在于提供一个共同的语言,使安全专业人员能够更好地理解攻击者的行为和目标&…...

在Ubuntu下搭建自己的以太坊私有链
最近要对链及链上应用进行压测,为了方便操作及分析问题,就自己搭建了一个eth私链。当前版本安装官方指引发现有卡点,于是决定整理一个文档,为其他有需要的朋友提供便捷操作,节约时间。 一、环境配置 linux操作系统:Ubuntu 20.04.6 LTS (Focal Fossa) go version: go1…...

巩固学习4
python中函数逆置的几种方法 s input()for i in range(len(s)-1,-1,-1):#从最后一位开始,步长为-1print(s[i],end)用for语句循环逆置 s input() s list(s) n len(s) for i in range(n//2):s[i],s[n-1-i] s[n-1-i],s[i]#从中间反转字符串 res "".j…...

Conda安装rasterio报错
Conda安装rasterio报错 文章目录 Conda安装rasterio报错问题解决参考 问题 在conda环境中安装rasterio包之后,本来可以正常运行的,但是之后又重新安装了一个gdal,导致原来的引用rasterio的包的程序不可正常运行了 conda install rasterio c…...
linux安装 mysql
环境:centOS8 一、安装 1 安装wget库 sudo yum -y install wget 2. 安装 mysql 换yum源 亲测成功!!!!!! 换yum源 1.下载对应版本的repo文件 wget -O CentOS-Base.repo http://mirrors…...
暴力法解决最近对问题和凸包问题-实现可视化
目录 最近对问题 凸包问题 最近对问题 顾名思义就是采用蛮力法求出所有点之间的距离,然后进行比较找出第一个最近对,一个一个进行比较。 大概思路就是如图(每个圈代表一个数对) 第一个和其他四个比较 第二个和其他三个比较 …...
[Kubernetes] Rancher 2.7.5 部署 k8s
server: 192.168.66.100 master: 192.168.66.101 node1: 192.168.66.102 文章目录 1.rancher server 安装docker2.部署k8s3.kubeconfig4.测试集群 1.rancher server 安装docker 所有主机开通ipv4 vi /etc/sysctl.conf#加入 net.ipv4.ip_forward 1#配置生效 sysctl -prancher…...
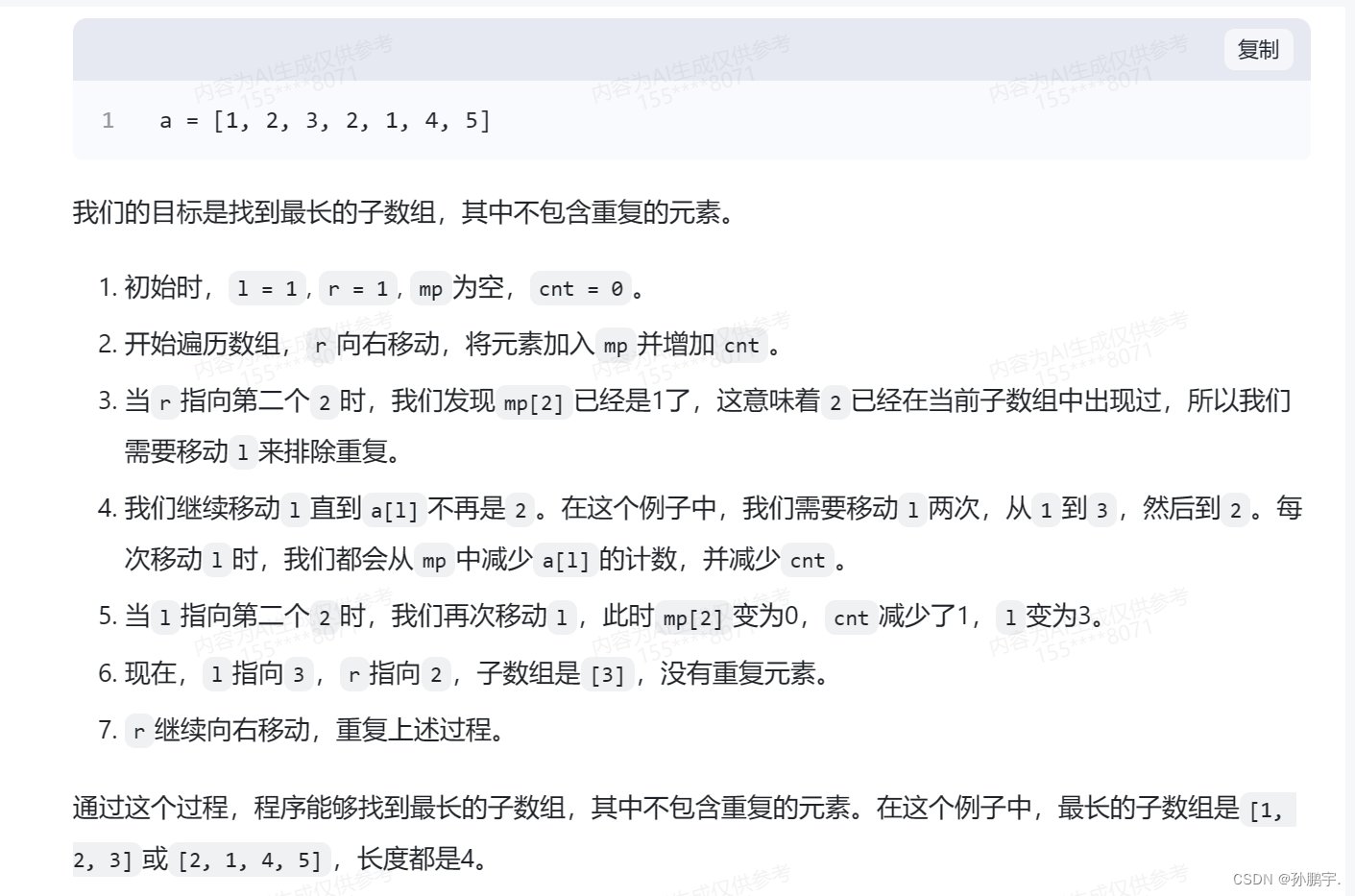
码题杯 世界警察 思想:双指针
https://www.matiji.net/exam/brushquestion/4/4446/16A92C42378232DEB56179D9C70DC45C 双指针 思路是这样的,首先r指针向右走,如果r指针遇到了和l指针一样的,那么l指针就,一直加到r指针的位置,此时a[l]a[r]࿰…...
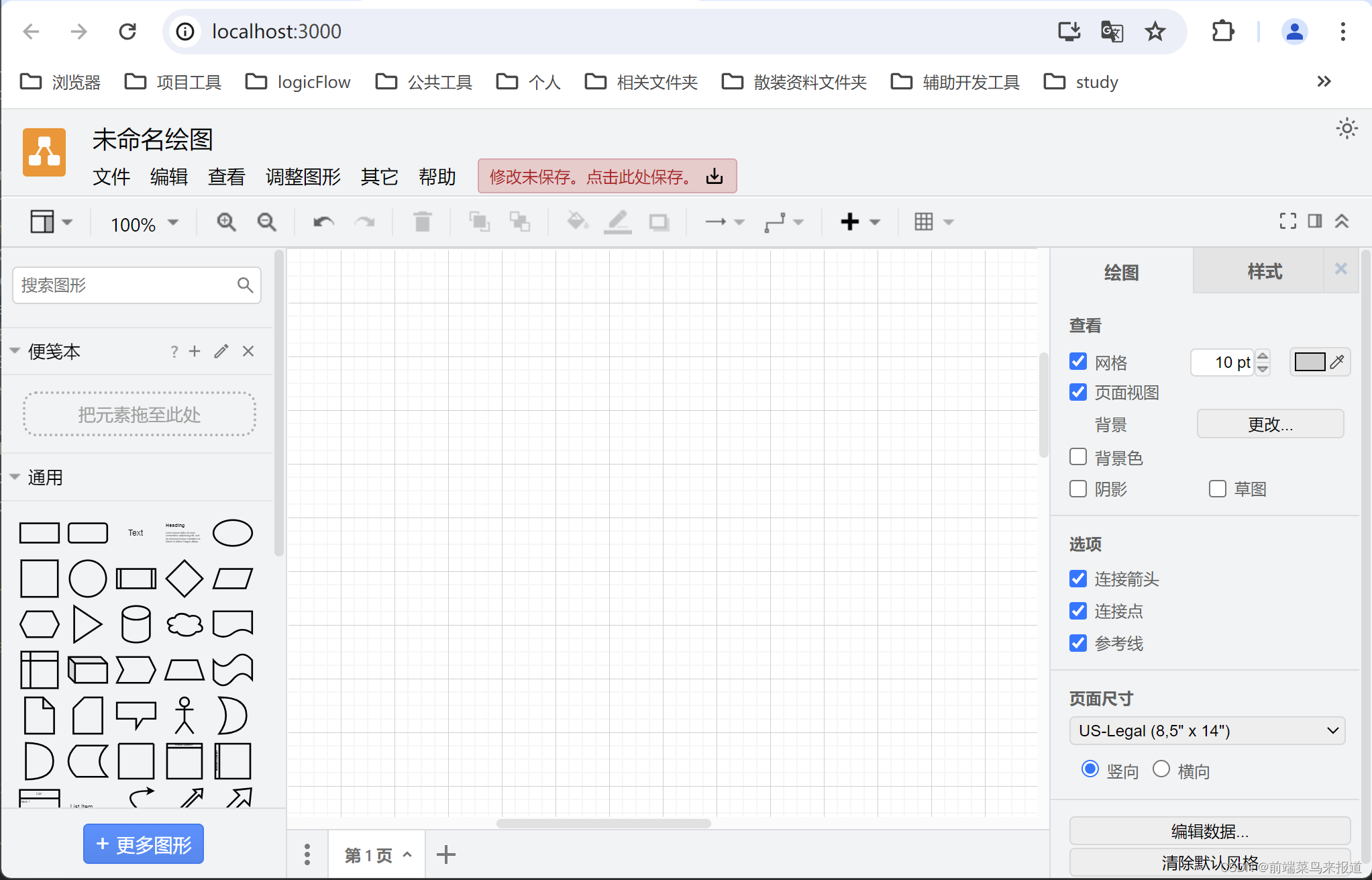
drawio 网页版二次开发(1):源码下载和环境搭建
目录 一 说明 二 源码地址以及下载 三 开发环境搭建 1. 前端工程地址 2. 配置开发环境 (1)安装 node.js (2)安装 serve 服务器 3. 运行 四 最后 一 说明 应公司项目要求,需要对drawio进行二次开发&…...

算法训练Day33 |● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
509. 斐波那契数 class Solution { public:int fib(int n) {if(n<1) return n;int pre2 0;int pre1 1;int result 0;for(int i2; i<n; i ){result pre1pre2;pre2 pre1;pre1 result;}return result;} };参考文章:代码随想录- 509. 斐波那契数 70. 爬楼梯…...
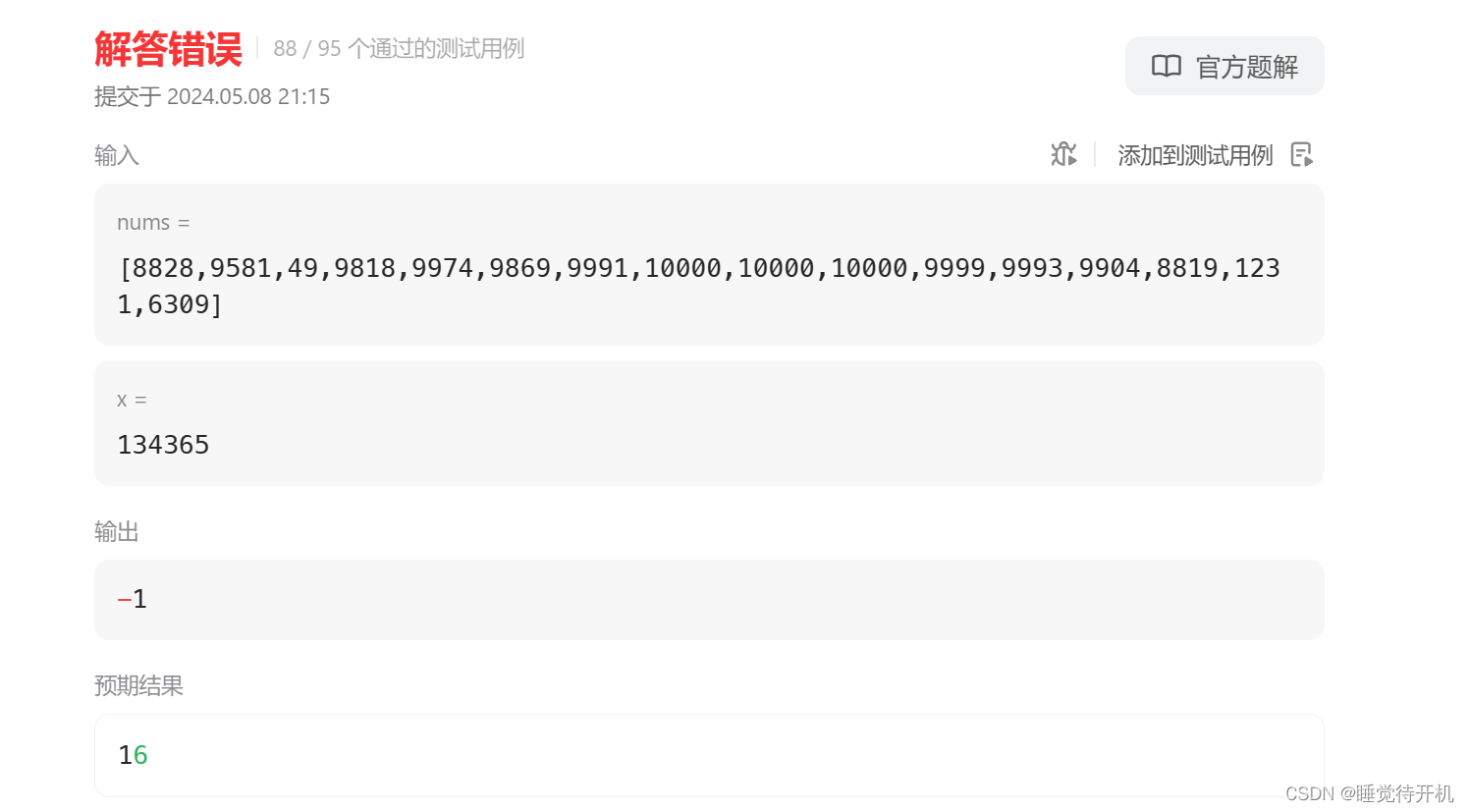
【算法】滑动窗口——将x减到0的最小操作数
本节博客主要是讲的我解“将x减到0的最小操作数”这道题的思路历程,从最开始的想法到代码提交的详细记录,有需要借鉴即可。 目录 1.题目2.代码示例3.细节3.1left越界3.2特殊情况 4.总结 1.题目 题目链接:LINK 看题目意思是就是给你一个数X&…...

《引爆流量获客技术》实操方法,手把手教你搭建盈利流量池
[1]-先导课.mp4 [2]-第1节:设计客户终身价值的方法和买客户思维.mp4 [3]-第2节:【渠道模型】解决谁是我的客户如何找到.mp4 [4]-第3节:【诱饵模型】解决 如何获得更多的客户.mp4 [5]-第4节:【钩子模型】解决让目标客户主动找你…...
【记录】常见的前端设计系统(Design System)
解释一下设计系统的定义,以及在国内,都有那些优秀的设计系统可以学习,希望可以帮到大家。 什么是设计系统(Design System)? 设计系统(Design System)是一套综合性的指导原则、组件和规则&…...

如何使用Whisper音频合成模型
Whisper 是一个通用语音识别模型,由 OpenAI 开发。它可以识别多种语言的语音,并将其转换为文本。Whisper 模型采用了深度学习技术,具有高准确性和鲁棒性。 1、技术原理及架构 Whisper 的工作原理:音频被分割成 30 秒的片段&#…...
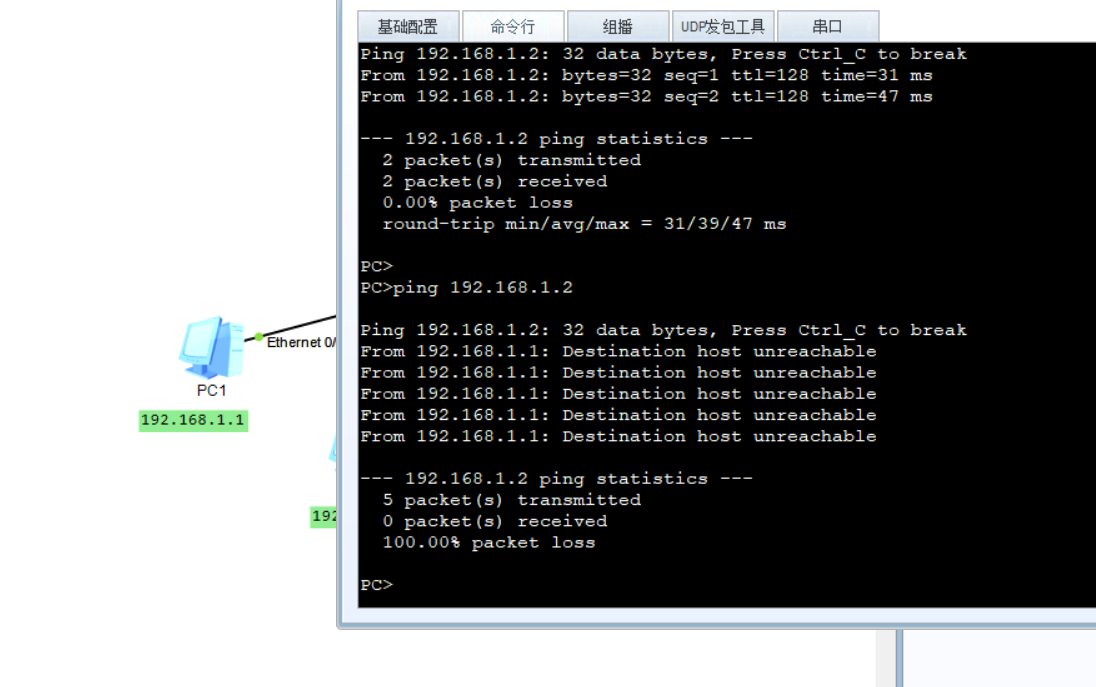
网络相关笔记
IPv4地址 IPv4地址通常以“点分十进制”形式书写,即四个0-255之间的十进制数,各数之间用英文句点(.)分隔,例如:192.0.2.1。总共32位的地址空间可以表示大约42亿个不同的地址。 IPv4地址结构包括ÿ…...

由C# yield return引发的思考
前言 当我们编写 C# 代码时,经常需要处理大量的数据集合。在传统的方式中,我们往往需要先将整个数据集合加载到内存中,然后再进行操作。但是如果数据集合非常大,这种方式就会导致内存占用过高,甚至可能导致程序崩溃。 …...

【问题解决】EasyExcel导出数据,并将数据中的实体类url转为图片
EasyExcel导出数据,并将数据中的实体类url转为图片 在导出excel数据时,用户要求把存储二维码url转为图片保存,然后研究了一下具体实现。 代码展示: public void exportData(String pointName, String districtName, String str…...
winform植物大战僵尸
winform植物大战僵尸 植物大战僵尸源码 半成品 需要的拿去学习 登陆注册选择关卡 向日葵 豌豆射手 双枪豌豆射手 项目获取: 项目获取:typora: typora/img (gitee.com) 备用项目获取链接1:yifeiyixiang/kamo: 源码下载 (github.com) 备用…...

Pointnet++改进即插即用系列:全网首发UIB轻量化模块
简介:1.该教程提供大量的首发改进的方式,降低上手难度,多种结构改进,助力寻找创新点!2.本篇文章对Pointnet++特征提取模块进行改进,加入UIB,提升性能。3.专栏持续更新,紧随最新的研究内容。 目录 1.理论介绍 2.修改步骤 2.1 步骤一 2.2 步骤二 2.3 步骤三...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
