[入门] Unity Shader前置知识(5) —— 向量的运算
在Unity中,向量无处不在,我想很多人都使用过向量类的内置方法 normalized() 吧,我们都知道该方法是将其向量归一化从而作为一个方向与速度相乘,以达到角色朝任一方向移动时速度都相等的效果,但内部具体是如何将该向量进行归一化的呢,本篇我们就来揭晓这个答案。
1. 相关概念
在学习向量的运算之前,我们先要了解一些有关概念:
标量(scalar)是一个只有大小,没有方向的物理量。
向量(vector)是一个有长度,也有方向的有向线段。
向量的模(magnitude)指的这个向量的长度。一个向量的长度可以是任意的非负数。模式一个标量。
向量的方向(direction)描述了这个向量在空间的指向。
2. 向量和标量的乘法/除法
以三维向量为例,向量和标量的乘法公式如下:
类似的,向量也可以被一个非零的标量相除,这等同于和这个标量的倒数相除:
下面是两个简单的例子:
3. 向量之间的加法和减法
我们可以对两个向量进行相加或相减,其结果是一个相同维度的新向量。只需要把两个向量的对应分量进行相加或相减即可,公式如下:
下面是两个简单的例子:
4. 向量的模
我们以三维向量为例,计算一个向量的模公式如下:
我们以一个二维向量(1, 1)为例,模的计算方式如下:
5. 向量的归一化
向量归一化(normalized vector)是指将该向量的模变为1,模为1的向量被称为单位向量(unit vector)。对任何给定的非零向量,把它转换成单位向量的过程就被称为归一化(normalization)。
通常,我们在向量的头上添加一个带帽符号来表示单位向量,例如。为了对向量进行归一化,我们可以将向量除以该向量的模来得到,公式如下:
我们以一个二维向量(1, 1)为例,该向量归一化的计算方式如下:
6. 向量之间的乘法
6.1. 点积
点积(dot product)的名称来源于这个运算符号:。点积的公式有两种形式,我们先看第一种公式:
它还有第二个公式:
由此公式我们可以得出:
当a、b两个向量都为单位向量,也就是和
都为1时,公式又可以简化为:
因此:
6.2. 叉积
叉积(cross product)的名称来源于它的符号:,同样这个叉号也不能省略它的计算公式为:
我们用一张图就可以清晰的描述它的运算规律:
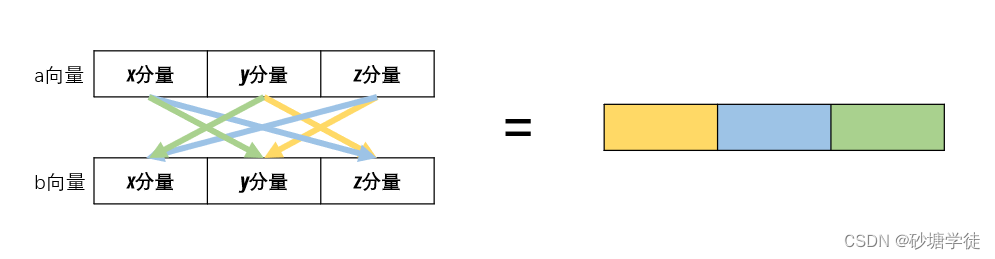
计算出来的向量是垂直于a、b所构成的平面的法向量。
相关文章:

[入门] Unity Shader前置知识(5) —— 向量的运算
在Unity中,向量无处不在,我想很多人都使用过向量类的内置方法 normalized() 吧,我们都知道该方法是将其向量归一化从而作为一个方向与速度相乘,以达到角色朝任一方向移动时速度都相等的效果,但内部具体是如何将该向量进…...

html的i标签 “\e905“ font-family 字体没有效果
一、html的i标签 “\e905” 没有效果 在HTML和CSS中,\e905 这样的字符通常与字体图标(Font Icons)或自定义字体(Custom Fonts)中的Unicode字符相关。具体来说,\e905 是一个Unicode转义序列,但它…...
 的用法及示例)
Golang reflect.MakeFunc() 的用法及示例
Golang 作为一门强类型语言,在某些场景下,我们需要动态地创建函数或者修改函数,这个时候就可以使用反射的方法去实现。在反射中,我们可以使用 reflect.MakeFunc() 方法来创建一个新的函数,本文我将介绍使用反射及其 Ma…...

深入学习和理解Django视图层:处理请求与响应
title: 深入学习和理解Django视图层:处理请求与响应 date: 2024/5/4 17:47:55 updated: 2024/5/4 17:47:55 categories: 后端开发 tags: Django请求处理响应生成模板渲染表单处理中间件异常处理 第一章:Django框架概述 1.1 什么是Django?…...
【MySQL】SQL基本知识点DDL(1)
目录 1.SQL分类: 2.DDL-数据库操作 3.DDL-表操作-创建 4.DDL-表操作-查询 5.DDL-表操作-数据类型 6.DDL-表操作-修改 1.SQL分类: 2.DDL-数据库操作 3.DDL-表操作-创建 注意:里面的符号全部要切换为英文状态 4.DDL-表操作-查询 5.DDL…...

短剧奔向小程序,流量生意如何开启?
随着移动互联网的飞速发展,小程序作为一种轻量级、易传播的应用形态,逐渐在各个领域展现出其独特的商业价值。而最近爆火的短剧小视频作为一种受众广泛的娱乐形式,与小程序结合后,不仅为观众提供了更为便捷的观看体验,…...
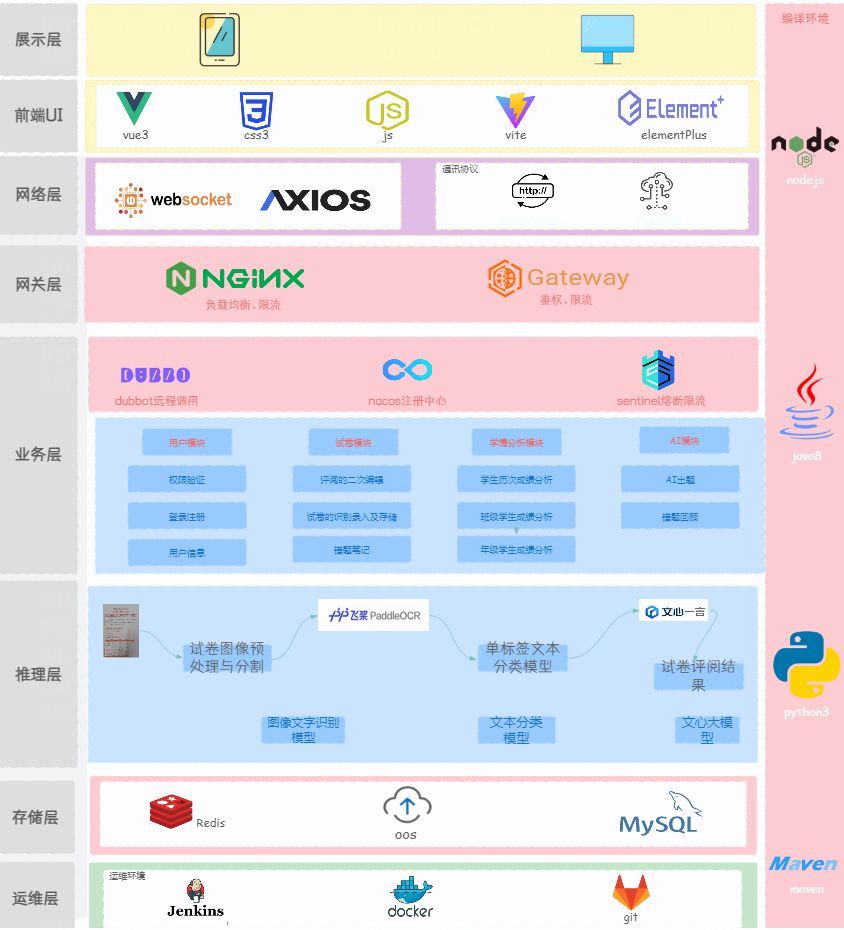
微服务下的技术栈架构解析
微服务是一种架构风格,它将一个复杂的应用拆分成多个独立自治的服务,每个服务负责应用程序中的一小部分功能。这些服务通过定义良好的API进行通信,通常是HTTP RESTful API或事件流。微服务架构的主要特点包括单一职责、自治性、可独立部署和扩…...
)
Mesa3D图形库与NIR(New Intermediate Representation)
Mesa 是一个开源图形库,为 Unix 和 Linux 系统提供了 OpenGL 和 Vulkan API 的实现。它也支持其他图形 API,如OpenCL、OpenGL ES 和 Vulkan。Mesa 项目的目标是为开源社区提供高性能的图形库,使得开源操作系统能够充分利用现代图形硬件。 Me…...
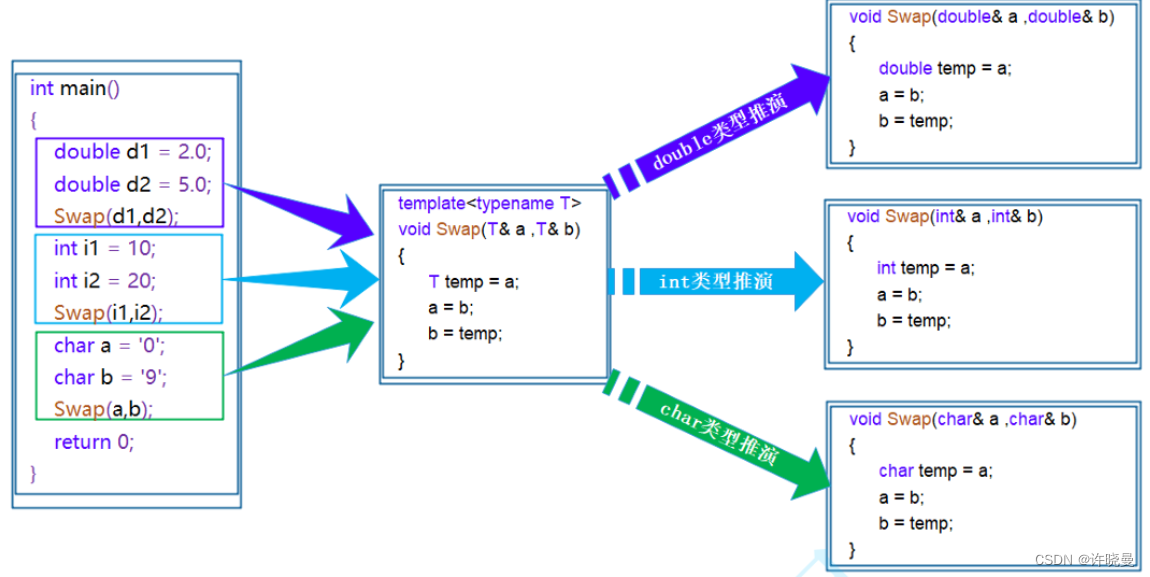
C++:模板初阶
文章目录 泛型编程函数模板概念函数模板格式函数模板的原理函数模板的实例化模板参数的匹配原则 模板类类模板的定义格式类模板实例化 泛型编程 如何实现一个通用的交换函数呢? 函数重载可以帮助我们完成 void Swap(int& left, int& right) {int temp l…...

为什么要学Python?学Python有什么用?
为什么要学Python?学Python有什么用? 在当今的数字化时代,编程已成为一项宝贵的技能。Python,作为一种流行的编程语言,因其易于学习和强大的功能而受到全球开发者的青睐。本文将探讨学习Python的原因和它的实际应用&am…...
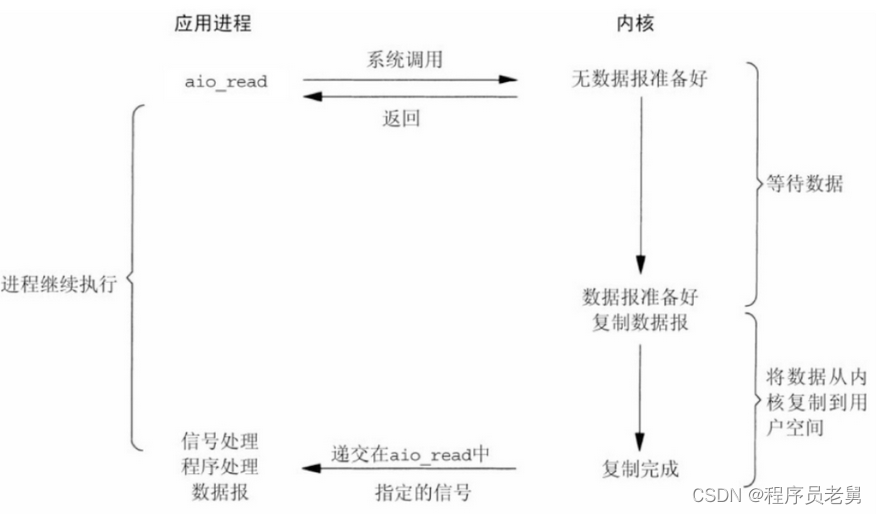
Linux磁盘IO、网络IO、零拷贝详解
一、什么是I/O? 在计算机操作系统中,所谓的I/O就是输入(input)和输出(output),也可以理解为读(read)和写(write),针对不同的对象,I/O模式可以划分…...

工业交换机外壳材质大比拼,看看哪种外壳适合你
在工业领域里,交换机就像我们的网络心脏,时刻跳动着确保信息畅通无阻。而它的外壳,就是保护这颗“心脏”的铠甲。今天,咱们就来聊聊这些铠甲——工业交换机外壳的材质和防护等级,看看它们如何守护我们的网络世界。 首…...

智慧公厕的技术基础、保障技术和应用价值
近年来,随着信息技术的快速发展,智慧公厕逐渐成为城市管理的热点项目。智慧公厕利用物联网技术与大数据、云计算、网络通信、自动化控制等先进技术相结合,公共厕所的管理变得更加快捷高效,实现了真正的智能化使用和智慧化管理。下…...

思腾合力受邀参加VALSE 2024视觉与学习青年学者研讨会
在充满学术氛围的五月,思腾合力荣幸受邀参加了于2024年5月5-7日在重庆举行的第十四届VALSE大会。作为视觉与学习领域的顶级交流平台,VALSE大会每年都吸引着全国专家与学者的目光。 本次大会不仅延续了往届的高水平学术研讨,还进一步拓宽了研究…...

geotrust dv通配符证书800
Geotrust是成立时间较久的正规CA认证机构,在过去的几十年间颁发了无数的SSL证书,这些SSL证书被各个开发者使用,受到大多数浏览器的信任。而Geotrust旗下的DV通配符证书因其广泛的应用范围受到了用户的青睐。今天就随SSL盾小编了解Geotrust旗下…...
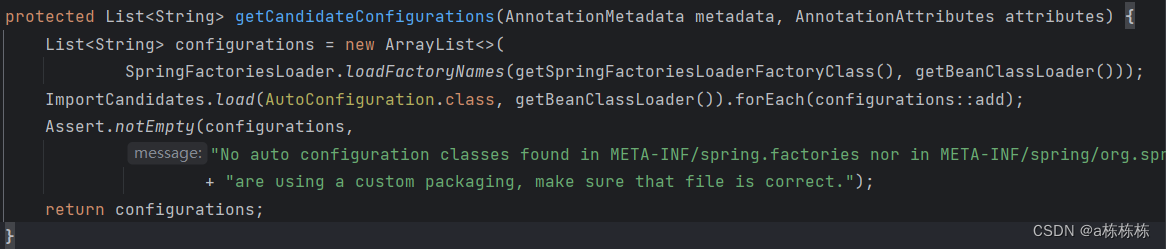
SpringBoot工作原理
优点:自动装配,起步依赖 起步依赖 原理就是maven的依赖传递 【A依赖B、B依赖C….,则我导入依赖A的时候,B,C都会被maven加载进来】 重点看看自动装配 概念: 当Spring容器启动后,一些配置类、…...
【Spring】Spring 整合 Junit、MyBatis
一、 Spring 整合 Junit <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache…...

【JVM基础篇】JVM入门介绍
JVM入门介绍 为什么学习JVM 岗位要求 解决工作中遇到的问题 性能调优 真实案例 导出超大文件,系统崩溃从数据库中查询超大量数据出错消费者消费来不及导致系统崩溃Mq消息队列接受消息导致的内存泄漏业务高峰期系统失去响应 初识JVM 什么是JVM? JV…...
理解函数对象)
《21天学通C++》(第二十一章)理解函数对象
什么是函数对象? 函数对象是一种特殊类型的类,它重载了函数调用操作符 operator(),使得类的实例可以像函数一样被调用。 什么是谓词? 谓词是指一个能够返回布尔值(true或false)的函数或函数对象 1.一元函数…...
2024.1.1 IntelliJ IDEA 使用记录
2024.1.1 IntelliJ IDEA 使用记录 下载设置文件编码maven 配置 插件可以中文语言包安装lombok 插件Smart Tomcat ( 根据需要安装)Smart Tomcat 配置 热部署(非必须的)解决Intellij IDEA运行报Command line is too long的问题 项目导入java 设置maven 配置…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
