Leetcode.剑指 Offer II 022 链表中环的入口节点
题目链接
Leetcode.剑指 Offer II 022 链表中环的入口节点 mid
题目描述
给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos来表示链表尾连接到链表中的位置(索引从 0开始)。 如果 pos是 -1,则在该链表中没有环。注意,pos仅仅是用于标识环的情况,并不会作为参数传递到函数中。
说明:不允许修改给定的链表。
示例 1:
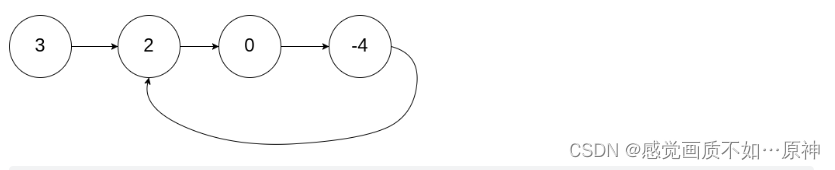
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:

输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
- 链表中节点的数目范围在范围 [0,1040, 10^40,104] 内
- −105<=Node.val<=105-10^5 <= Node.val <= 10^5−105<=Node.val<=105
pos的值为-1或者链表中的一个有效索引
分析:快慢指针
我们用两个指针 fast和slow,初始都指向 head,fast每次走两步,slow每次走一步。
如果链表存在环,那么 fast和 slow一定会在环中相遇。
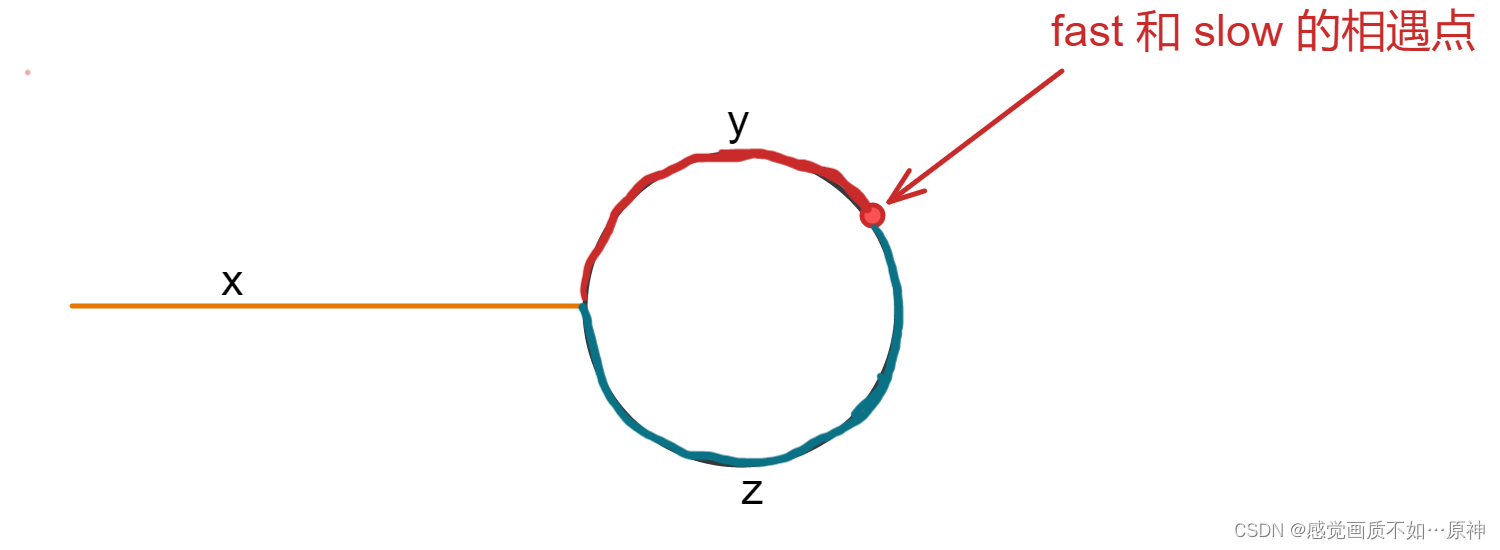
因为fast比slow要快1步,所以当 slow走过的距离为 x + y到达相遇点时,fast其实已经在环里转了若干圈了(这里假设是 n圈)。
所以 fast走过的路程为 ,x+n∗(y+z)+yx + n * (y + z) + yx+n∗(y+z)+y
又因为 fast走过的路程 应该是 两倍slow走过的路程,即 x+n∗(y+z)+y=2∗(x+y)x + n * (y + z) + y = 2 * (x + y)x+n∗(y+z)+y=2∗(x+y)
化简得 : x=(n−1)∗(y+z)+zx = (n - 1) * (y + z) + zx=(n−1)∗(y+z)+z,即从相遇点走 z的路程,再走若干圈,就是 x的路程。(我们只需要走 0 圈即可),即 x=zx = zx=z。
当 fast和 slow相遇时,让 fast重新指向头节点 head,fast和slow同时移动,当他们再次相遇时的点,就是环的起点。
时间复杂度: O(n)O(n)O(n)
C++代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {if(head == nullptr) return nullptr;ListNode *fast = head , *slow = head;while(fast && fast->next){slow = slow->next;fast = fast->next->next;//两者相遇if(slow == fast){fast = head;while(slow != fast){slow = slow->next;fast = fast->next;}return slow;}}return nullptr;}
};Java代码:
/*** Definition for singly-linked list.* class ListNode {* int val;* ListNode next;* ListNode(int x) {* val = x;* next = null;* }* }*/
public class Solution {public ListNode detectCycle(ListNode head) {if(head == null) return null;ListNode fast = head;ListNode slow = head;//fast 或 fast.next 为 null , 说明链表没有环while(fast != null && fast.next != null){slow = slow.next;fast = fast.next.next;//快慢指针相遇了,fast 重新回到头节点 head,快慢指针再同时移动if(slow == fast){fast = head;while(fast != slow){fast = fast.next;slow = slow.next;}return fast;}}return null;}
}相关文章:

Leetcode.剑指 Offer II 022 链表中环的入口节点
题目链接 Leetcode.剑指 Offer II 022 链表中环的入口节点 mid 题目描述 给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。 为了表示给定链表中的环&#…...

4种不同编程语言的打印方式
意义 打印方式是编程中不可或缺的一部分,它可以帮助开发人员有效地调试和测试代码,并提供有用的信息来监视程序的运行状态和性能。 编程语言中的打印方式是指将程序输出到终端或控制台上进行显示。这个功能在编程中非常重要,因为它可以帮助开…...

websocket介绍
我们聊聊轮询技术,什么是轮询?轮询就是在特定的时间间隔,由浏览器对服务器发出HTTP请求,然后由服务器返回最新的数据给客户端的浏览器。 轮询分为两种: 短轮询:通过不断的向服务端发送数据,客户端发送Request,服务端直接返回Response(不管服务端数据有没有改变)。长轮…...
,C,D)
Educational Codeforces Round 144 (Rated for Div. 2),C,D
C. Maximum Set 思路: 我们求最大数组,显然是L一直乘2,直到再乘2就越过区间位置。我们说过,再乘一个2就不行,那么我们除一个2,换句话说,就是再乘一个4就不行了。发现,我们可能有机会乘一个3&a…...
【redis学习篇】Redis三种持久化方式详解
官方文档 一、Redis持久性 Redis如何将数据写入磁盘 持久性是指将数据写入持久存储,如固态磁盘(SSD)。Redis提供了一系列持久性选项。其中包括: RDB(快照):RDB持久性以指定的时间间隔执行数据…...

垃圾回收中的分代年龄
为什么CMS里的分代年龄是6而不是15 CMS (Concurrent Mark Sweep) 是一种基于分代的垃圾收集器,其中分代年龄指的是一个对象在年轻代中经历了多少次垃圾收集。在 CMS 中,当一个对象的分代年龄达到阈值时,就会被晋升到老年代中。 在 CMS 中&a…...

蓝桥杯-左移右移(2022国赛)
蓝桥杯-左移右移1、问题描述2、解题思路与代码实现2.1 方法一:使用LinkedList双向链表实现(50%)2.2 方法二:使用HashMap左右临界值实现(100%)1、问题描述 小蓝有一个长度为 N 的数组, 初始时从左到右依次是 1,2,3,…N 。 之后小蓝对这个数组进行了 M 次操…...

你还在手撸SQL?ChatGPT笑晕在厕所
文章目录你还在手撸SQL?ChatGPT笑晕在厕所一、背景二、面向Chat编程1. 数据库设计2. 建表语句3. 加中文注释4. 数据模拟5. 查询成绩6. 修改课程任课老师7. 删除课程8. 删除一个有关联数据的课程总结你还在手撸SQL?ChatGPT笑晕在厕所 一、背景 经典3表设…...

【Redis】Redis慢查询
文章目录慢查询记录慢查询两个配置参数修改配置参数慢查询日志慢查询记录 我们都知道像mysql等持久化数据库会有慢查询日志,其实Redis中也有慢查询日志的功能。慢查询就是系统在执行命令的前后计算每条命令的执行时间,如果超过我们预设的时间,…...

【Kubernetes】第二十一篇 - k8s 项目部署流程和操作梳理
一,前言 上一篇,介绍了 k8s 污点和容忍度; 在了解前面 k8s 介绍之后,设计并完成一个前后端项目的部署和持续集成; 本篇,介绍基于 k8s 项目部署流程设计; 二,项目部署流程设计 本…...
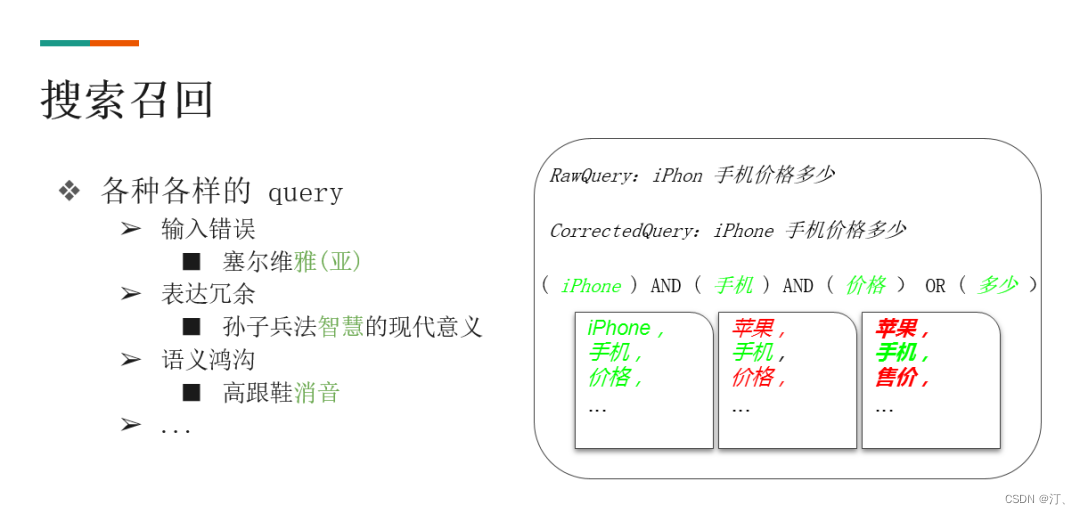
推荐系统[九]项目技术细节讲解z2:搜索Query理解[Term Weight、Query 改写、同义词扩写]和语义召回技术
搜索Query理解和语义召回技术 随着用户规模和产品的发展, 搜索面临着越来越大的 query 长尾化挑战,query 理解是提升搜索召回质量的关键。本次将介绍搜索在 query term weighting,同义词扩展,query 改写,以及语义召回等方向上的实践方法和落地情况。 1.面临问题:长尾 qu…...
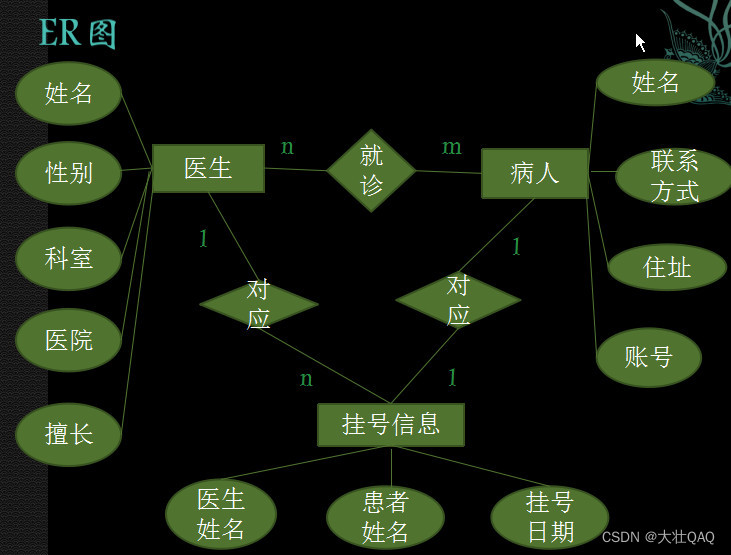
【项目精选】基于SSH的医院在线挂号系统(视频+论文+源码)
点击下载源码 医院挂号系统主要用于实现医院的挂号,前台基本功能包括:用户注册、用户登录、医院查询、挂号、取消挂号、修改个人信息、退出等。 后台基本功能包括:系统管理员登录、医院管理、科室管理、公告管理、退出系统等。 本系统结构如…...

Pandas库:从入门到应用(一)
一、Pandas简介 pandas是 Python 的核⼼数据分析⽀持库,提供了快速、灵活、明确的数据结构,旨在简单、直观地处理关系型、标记型数据。pandas是Python进⾏数据分析的必备⾼级⼯具。 pandas的主要数据结构是 **Series(**⼀维数据)与 DataFrame (⼆维数据…...
、concat_ws()、group_concat()函数使用)
MySQL中concat()、concat_ws()、group_concat()函数使用
在平时工作中,经常记不清或者记混他们的用法,正好有时间就记录一下~concat()函数语法:concat(str1, str2, int1...)例如执行sql:SELECT CONCAT(id,USERNAME,USER_PHONE) FROM tb_user输出查询结果为: 1test15216756754…...

【JavaEE初阶】第四节.文件操作 和 IO (上篇)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、文件 1.1 文件的概念 1.2 文件的路径二、 Java中文件系统操作 2.1 File类的属性 2.2 File类的构造方法 2.3 File类的方法 …...

开源免费堡垒机Teleport堡垒机的安装
准备:纯净centos7系统一个作为堡垒机,若干个linux系统或windows系统服务器作为受保护的服务器 堡垒机IP:192.168.1.15 服务器IP:192.168.1.10 1、teleport安装 下载地址: https://www.tp4a.com/static/download/teleport-server-linux-x64-3.6.4-b3.tar.gz xshell上传压缩…...

图形报表ECharts
图形报表ECharts1 图形报表ECharts1.1 ECharts简介-富客户端图表库ECharts缩写来自Enterprise Charts,商业级数据图表,是百度的一个开源的使用JavaScript实现的数据可视化工具,可以流畅的运行在PC和移动设备上,兼容当前绝大部分浏…...

便捷式储能电源核心技术--单相逆变器设计
便捷式储能电源核心技术–单相逆变器设计 1.逆变器的规格参数 输入电压直流400V输出电压交流rms220V开关频率10kHz滤波电容6.23uF控制方式单极性倍频2.视频学习链接 视频学习链接 3.主电路仿真设计...

Gamma矫正
Gamma 曲线Gamma校正被使用在8位RGB图中。用来解决在有限的存储空间中保存尽可能多的人类感受敏感的色彩内容。Gamma 矫正Gamma校正的方式就是采样时,和输出到显示器给人类看时,对亮度进行的调整.如采样时 Gamma1/2.2 调亮Gamma,如显示时 Gamma2.2 调暗Gamma实际亮度…...

速懂cookie,session,token
文章目录cookiesessiontoken区别cookie 是浏览器提供的一种能力,可以在每次发起请求前,带上cookie里面的内容(一些key,value值) 分类: 会话级cookie:默认情况,就是会话级cookie&…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
