Codeforces Round 855 (Div. 3) A-E2
比赛链接:Dashboard - Codeforces Round 855 (Div. 3) - Codeforces
A:模拟

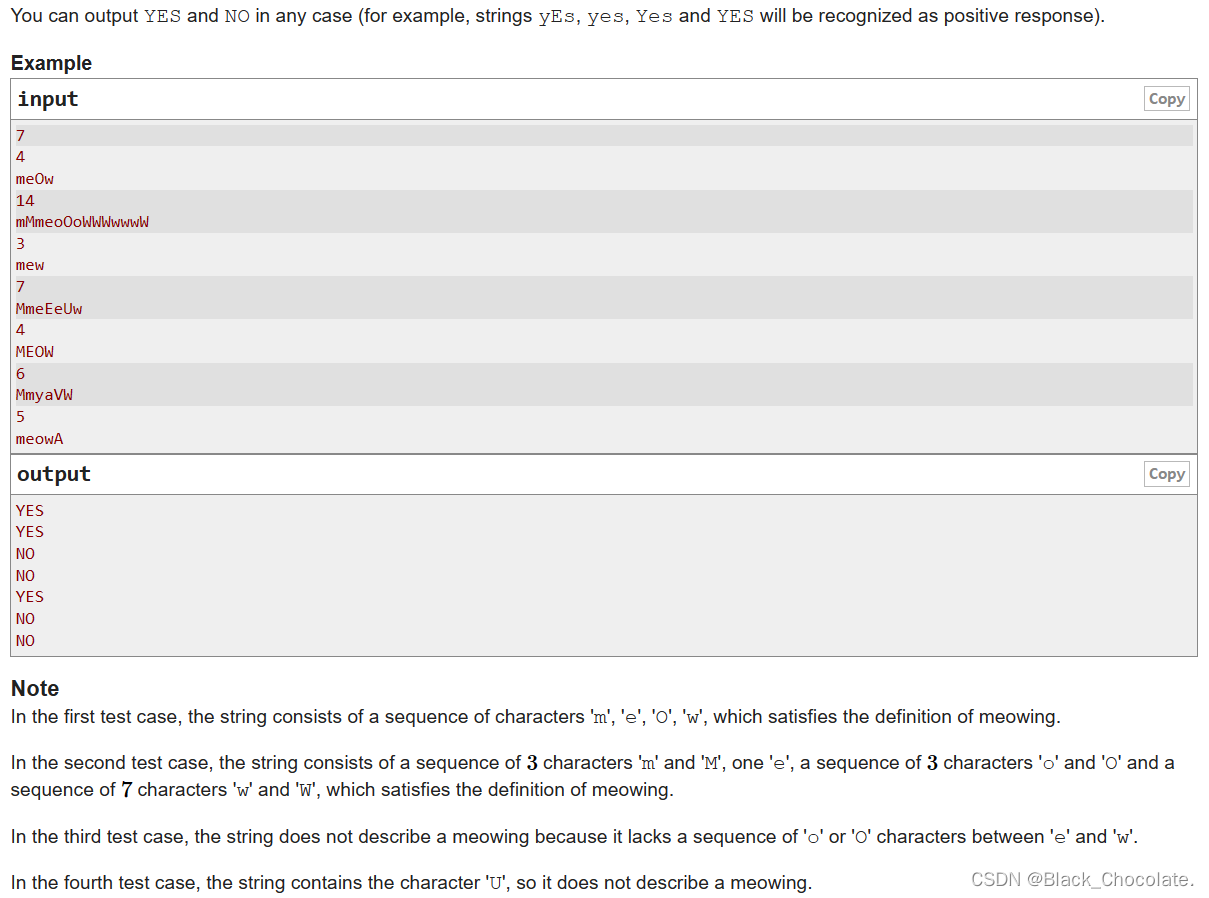 题意:给定一个字符串,问这个字符串是不是猫叫。定义是猫叫得字符串:
题意:给定一个字符串,问这个字符串是不是猫叫。定义是猫叫得字符串:
1:必须由大写或小写得'M(m)','E(e)','O(o)','W(w)'组成
2:字符串起始必须是M(大写或者小写都行)紧跟其后必须是E,接着是O,接着是W,然后结束。
分析:根据条件,将字符串扫一遍即可
代码:
#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}// a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%pinline void solve(){int n,i=0;string s;cin>>n>>s;if(n<4||(s[0]!='M'&&s[0]!='m')){cout<<"NO\n";return;}while(s[i]=='M'||s[i]=='m') i++;if(s[i]!='E'&&s[i]!='e'){cout<<"NO\n";return;}while(s[i]=='E'||s[i]=='e') i++;if(s[i]!='O'&&s[i]!='o'){cout<<"NO\n";return;}while(s[i]=='O'||s[i]=='o') i++;if(s[i]!='W'&&s[i]!='w'){cout<<"NO\n";return;}while(s[i]=='W'||s[i]=='w') i++;if(i==n) cout<<"YES\n";else cout<<"NO\n";
}signed main(){fast;int T;cin>>T;while(T--) solve();
} B:贪心


题意: 给定一个字符串,相同字符的大小写为一个匹配对(例如:Aa)。你可以使用任意次操作,使得将大写字母改为小写字母,或者小写字母改为大写字母。问最多有多少个匹配对
分析:我们发现,尽可能的使用完操作次数,我们才会得到最大匹配对数。我们只需要记录一下相同字母对应的大小写个数,然后可以先计算原始的匹配对,再计算操作后的匹配对数。具体看代码
#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}// a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int u[N],l[N];inline void solve(){int n,k;string s;cin>>n>>k>>s;memset(u,0,sizeof u);memset(l,0,sizeof l);for(int i=0;i<n;i++){if(isupper(s[i])) u[s[i]-'A']++;else l[s[i]-'a']++;}int ans=0;for(int i=0;i<26;i++){int minn=min(u[i],l[i]);ans+=minn;u[i]-=minn;l[i]-=minn;if(u[i]>=2){if(u[i]/2<=k) ans+=u[i]/2,k-=u[i]/2;else ans+=k,k=0;}else if(l[i]>=2){if(l[i]/2<=k) ans+=l[i]/2,k-=l[i]/2;else ans+=k,k=0;}}cout<<ans<<"\n";
}signed main(){fast;int T;cin>>T;while(T--) solve();
} C:模拟+贪心(大根堆)

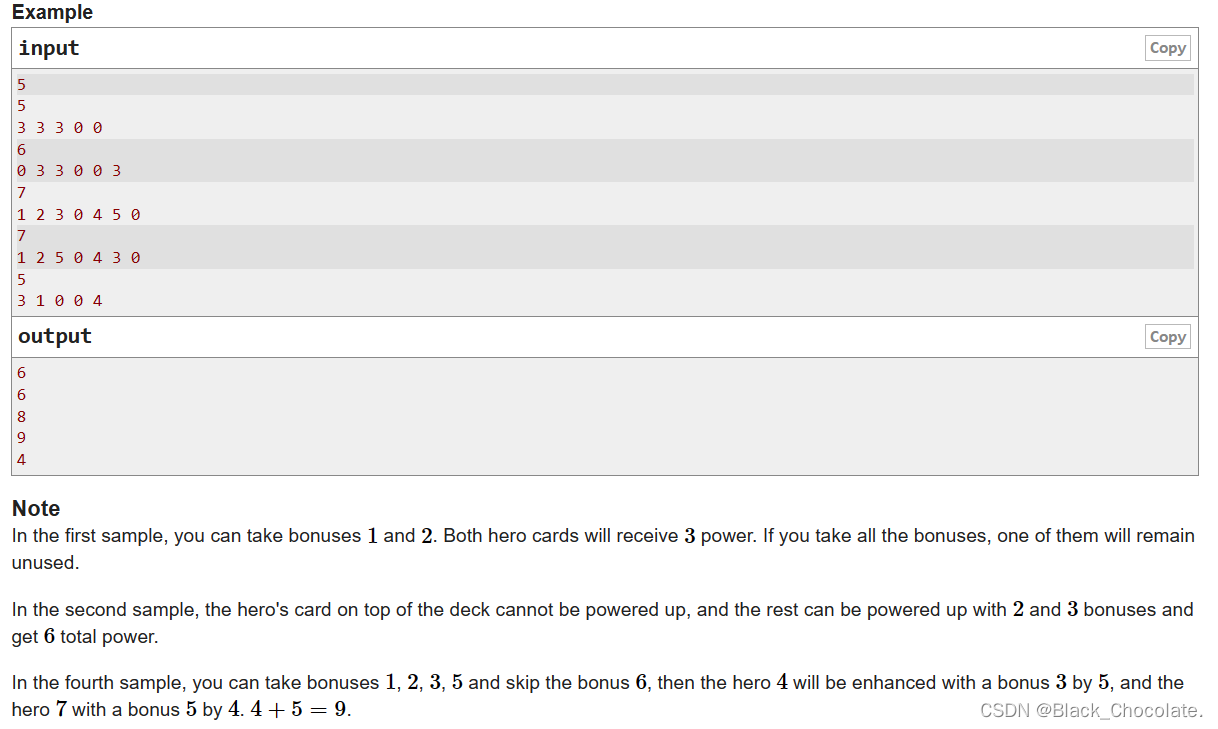 题意:你的初始分数为0。给定一堆牌,每个牌有一定的数字,给定顺序去摸取。如果摸到非0牌,则可以选择将此牌放在自己牌堆的堆顶,或者放弃这张牌。如果摸到数字为0的牌,则自己牌堆堆顶的数字会加到你的分数里面,并且标记这张牌已经使用过,问你能得到的最大分数。
题意:你的初始分数为0。给定一堆牌,每个牌有一定的数字,给定顺序去摸取。如果摸到非0牌,则可以选择将此牌放在自己牌堆的堆顶,或者放弃这张牌。如果摸到数字为0的牌,则自己牌堆堆顶的数字会加到你的分数里面,并且标记这张牌已经使用过,问你能得到的最大分数。
分析:根据题意,我们发现,在摸到非0牌之前,我们要将最大的数字放在堆顶,那么这是一个动态维护最大值的过程,因此我们可以使用大根堆。大根堆的pop()操作即为已经使用的牌。
代码:
#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}// a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int a[N];inline void solve(){int n;cin>>n;priority_queue<int>q;for(int i=1;i<=n;i++) cin>>a[i];int ans=0,cnt=1;while(1){if(cnt>n) break;while(cnt<=n&&a[cnt]!=0) q.push(a[cnt++]);while(cnt<=n&&a[cnt]==0){if(!q.size()){cnt++;continue;}else{ans+=q.top();q.pop();cnt++;}}}cout<<ans<<"\n";
}signed main(){fast;int T;cin>>T;while(T--) solve();
} D:思维

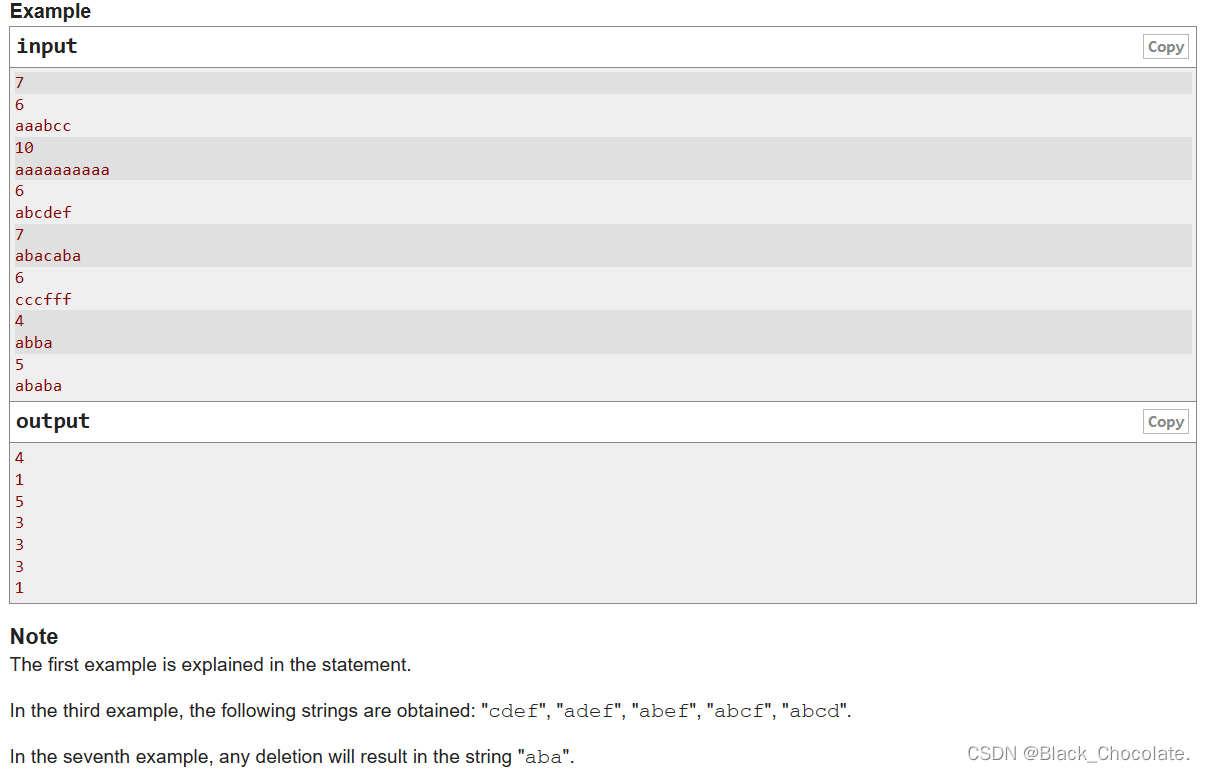
题意:给定字符串 s,你可以移除其中两个连续的字母。问操作之后你所能得到的不同字符串的数量是多少
分析:我们发现,如果这样一组字符串:aba,那么删掉两个相邻的元素,所得的结果串是一样的。那么我们可以得出一个结论:如果,那么就说明有一个重复串的出现。
此外还有一个结论可以从样例得出:如果一个长度为n的串所含的不同字符个数为n,那么可以得到n-1个不同的串。因此,我们只需要减掉重复串的个数即可。
代码:
#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}// a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int a[N];inline void solve(){int n;string s;cin>>n>>s;int ans=0;for(int i=0;i<n-2;i++){if(s[i]==s[i+2]) ans++;}cout<<n-ans-1<<"\n";
}signed main(){fast;int T;cin>>T;while(T--) solve();
} E:思维

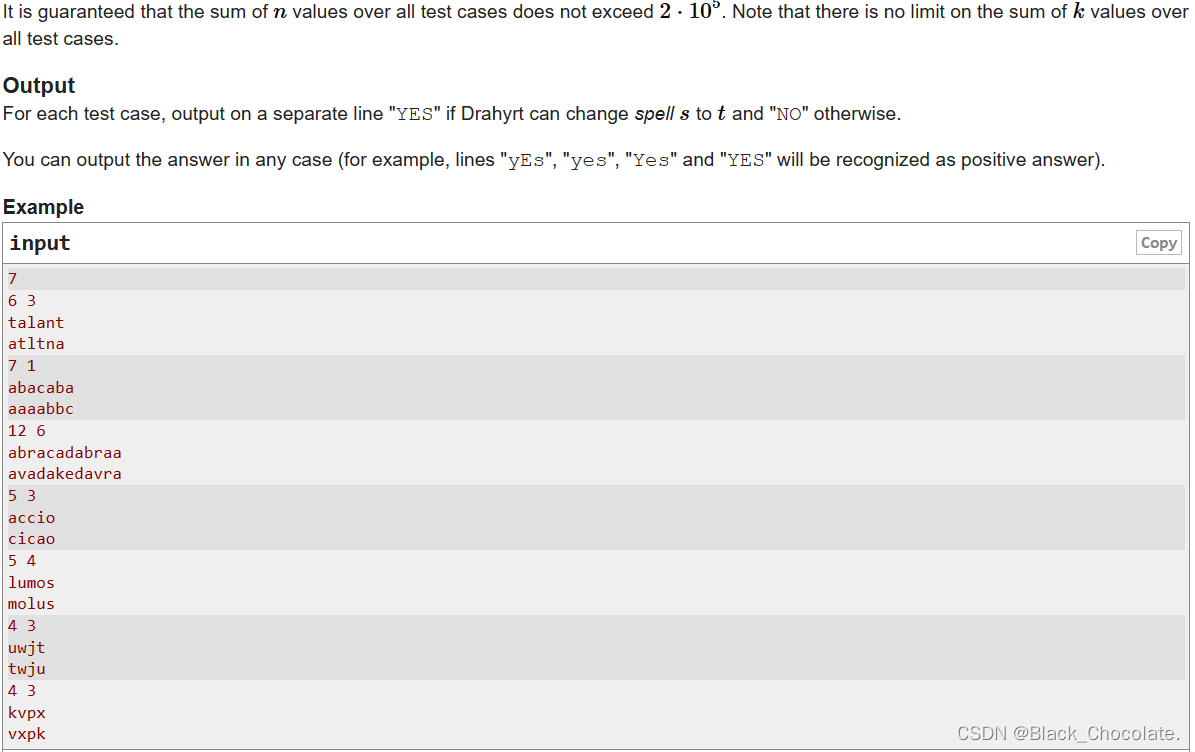
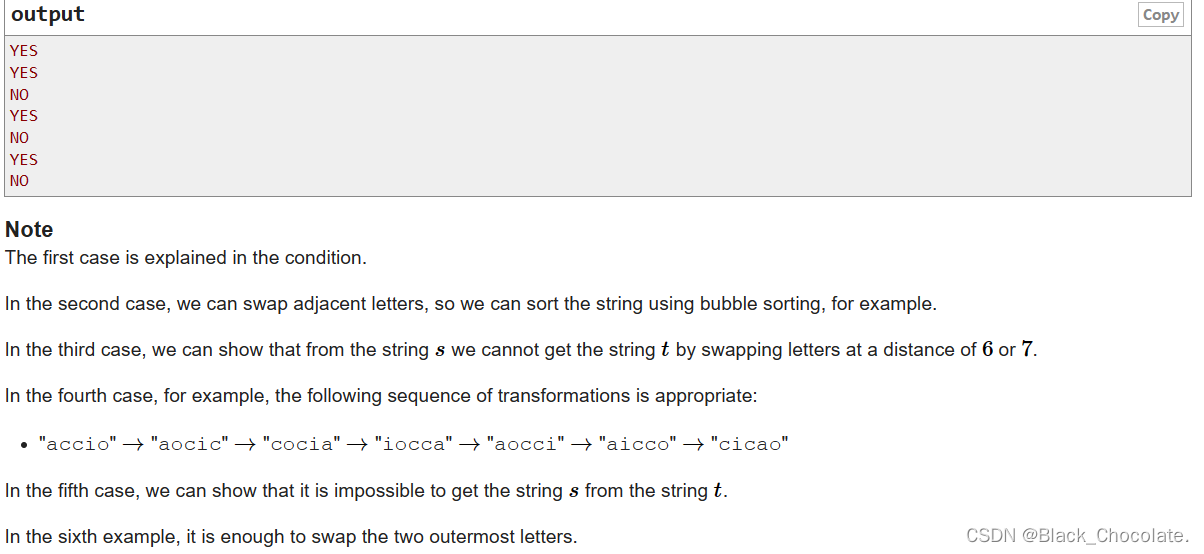
题意:给定两个字符串和k,字符串可以将下标 和|i−j|=k和|i−j|=k+1 得两个字符 ,ai,aj 发生交换
分析:通过手撸样例可以发现:如果当n=5,k=3的时候,满足条件的点为:[1,4],[1,5],[2,5]。然后你会发现:点1,2,4,5的位置可以任意交换。位置3则不能交换。所以思路很显然了。
首先判断两个字符串中包含的字符数是否相同,再判断不能交换位置的点上的字符是否相同。
代码:
#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}// a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%pinline bool pd(string a,string b){map<char,int>mp1,mp2;for(int i=0;i<a.size();i++) mp1[a[i]]++;for(int i=0;i<b.size();i++) mp2[b[i]]++;for(auto x:a){if(mp1[x]!=mp2[x]) return false;}return true;
}inline void solve(){int n,k;string s,t;cin>>n>>k>>s>>t;if(!pd(s,t)){cout<<"NO\n";return;}bool ok=true;for(int i=0;i<n;i++){if(i<k&&n-i-1<k&&s[i]!=t[i]){ok=false;break;}}if(ok) cout<<"YES\n";else cout<<"NO\n";
}signed main(){fast;int T;cin>>T;while(T--) solve();
} 相关文章:

Codeforces Round 855 (Div. 3) A-E2
比赛链接:Dashboard - Codeforces Round 855 (Div. 3) - Codeforces A:模拟 题意:给定一个字符串,问这个字符串是不是猫叫。定义是猫叫得字符串: 1:必须由大写或小写得M(m),E&…...

Spark Yarn 运行环境搭建
文章目录Spark Yarn 运行环境搭建1、解压缩文件2、修改配置环境文件3、配置历史服务器Spark Yarn 运行环境搭建 1、解压缩文件 将spark3.2.3的压缩包上传到 linux /opt/software 目录下 输入命令: tar -zxvf spark-3.2.3-bin-hadoop3.2-scala2.13.tgz -C /opt/ 解…...

SpringMVC 页面跳转指南:转发和重定向的实现与比较
SpringMVC 是一款非常流行的 Java Web 框架,它提供了丰富的特性和功能,使得开发者可以轻松地开发 Web 应用程序。其中,转发和重定向是 SpringMVC 中非常常见的两个操作,它们可以用于控制请求的流转和页面的跳转。本文将深入探讨 S…...
ModStartCMS v5.9.0 后台浅色模式,系统样式升级
ModStart 是一个基于 Laravel 模块化极速开发框架。模块市场拥有丰富的功能应用,支持后台一键快速安装,让开发者能快的实现业务功能开发。 系统完全开源,基于 Apache 2.0 开源协议,免费且不限制商业使用。 功能特性 丰富的模块市…...

2020蓝桥杯真题反倍数 C语言/C++
题目描述 给定三个整数 a,b,c,如果一个整数既不是 a 的整数倍也不是 b 的整数倍还不是 c 的整数倍,则这个数称为反倍数。 请问在 1 至 n 中有多少个反倍数。 输入描述 输入的第一行包含一个整数 n。 第二行包含三个整数a,b,c,相邻两个数之…...

PTA:L1-025 正整数A+B、L1-026 I Love GPLT、L1-027 出租(C++)
目录 L1-025 正整数AB 问题描述: 实现代码: L1-026 I Love GPLT 问题描述: 实现代码: L1-027 出租 问题描述: 实现代码: 原理思路: 出租那道题有点意思哈 L1-025 正整数AB 问题描述…...
状态机的Go语言实现版本
一、状态机 1. 定义 有限状态机(Finite-state machine, FSM),简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。 2. 组成要素 现态(src state):事务当前所处的状…...

第2章 线程安全与共享资源竞争
第2章 线程安全与共享资源竞争 2.1 synchronized同步介绍 synchronized要解决的是共享资源冲突的问题。当共享资源被任务使用时,要对资源提前加锁。所有任务都采用抢占模式,即某个任务会抢先对共享资源加上第一把锁。如果这是一个排他锁,…...

77. writerows写入多行
文章目录1. 目标任务2. 准备工作3. writerow单行写入4. writerows多行写入5. a以追加的模式写入值6. 总结1. 目标任务 新建【各班级成绩】文件夹; 在该文件夹下新建一个【1班成绩单.csv】文件; 在该文件中写入下面的内容: 成绩 姓名 刘一…...

STM32MP157-Linux输入设备应用编程-多点触摸屏编程
文章目录前言多点触摸屏tslib库简介tslib库移植tslib库函数使用打开触摸屏设备配置触摸屏设备打开并配置触摸屏设备读取触摸屏设备多点触摸屏程序编写触点数据结构体定义事件定义计算触点数量判断单击、双击判断长按、移动判断放大、缩小外部调用代码流程图(草图&am…...
)
mybatis-plus的一般实现过程(超详细)
MyBatis-Plus 是 MyBatis 的增强工具,在 MyBatis 的基础上提供了许多实用的功能,如分页查询、条件构造器、自动填充等。下面是 MyBatis-Plus 的完整代码实现流程: ①、引入 MyBatis-Plus 依赖 在 Maven 中,可以通过以下方式引入 …...
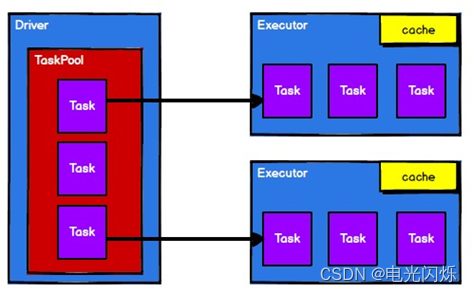
Spark(5):RDD概述
目录 0. 相关文章链接 1. 什么是RDD 2. RDD核心属性 3. 执行原理 0. 相关文章链接 Spark文章汇总 1. 什么是RDD RDD(Resilient Distributed Dataset)叫做弹性分布式数据集,是 Spark 中最基本的数据处理模型。代码中是一个抽象类&#x…...

面向对象 - 继承
Hello , 各位同学朋友大家好啊, 今天给大家分享的技术呢, 是面向对象三大特征之一的继承,我们今天主要按照以下几个点, 展开继承的讲解。目录 :* 继承的介绍* 继承的好处和弊端* 继承中成员访问特点 - 成员变量* 继承中成员访问特点 - 成员方法* 方法重写* 继承中成…...

计算机网络的166个概念你知道几个 第十二部分
计算机网络安全安全通信的四大要素:机密性、保温完整性、端点鉴别和运行安全性。机密性:报文需要在一定程度上进行加密,用来防止窃听者截取报文。报文完整性:在报文传输过程中,需要确保报文的内容不会发生改变。端点鉴…...

【RabbitMQ】RabbitMQ各版本的兼容性与技术支持时限
今天在研究RabbitMQ的监控时,发现这个消息队列软件的版本真的很令人崩溃,版本众多,且组件之间还存在版本的兼容性,此外各个组件还对操作系统存在兼容性关系。为了帮大家节省一些查阅官方文档的时间,我把官方文档里面涉…...
【Git】P5 Git 远程仓库(3)pull 发生冲突
pull 发生冲突冲突在什么场景下发生?为什么要先 pull 再 push构建一个冲突场景初始开始操作:程序员2:程序员1:程序员2:发生冲突:查看冲突:解决冲突:冲突在什么场景下发生?…...

关于世界坐标系,相机坐标系,图像坐标系,像素坐标系的一些理解
关于世界坐标系,相机坐标系,图像坐标系,像素坐标系的一些理解前言一、各坐标系的含义二、坐标系转换1.世界坐标系与相机坐标系(旋转与平移)2.相机坐标系与图像坐标系(透视)3.图像坐标系与像素坐…...

企业防护ddos的注意事项,你知道吗?
DDoS,分布式拒绝服务攻击,是指处于不同位置的多个攻击者同时向一个或数个目标发动攻击,或者一个攻击者控制了位于不同位置的多台机器并利用这些机器对受害者同时实施攻击。在当下,DDoS 攻击是非常常见的一种攻击方式,大…...
RocketMQ如何测试
RocketMQ如何测试MQ简介RocketMQRocketMQ测试点MQ简介 MQ:Message Queue,即消息队列,是一种应用程序之间的消息通信,简单理解就是A服务不断的往队列里发布信息,另一服务B从队列中读取消息并执行处理,消息发…...

SpringBoot中的bean注入方式和原理介绍
Spring Boot是一个非常流行的Java框架,它可以帮助开发者快速地构建高效、健壮的应用程序。其中一个重要的功能就是依赖注入,也就是将一个对象注入到另一个对象中,以便它们可以相互协作。在Spring Boot中,依赖注入是通过bean实现的…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
