python实现波士顿房价预测
波士顿房价预测
目标
这是一个经典的机器学习回归场景,我们利用Python和numpy来实现神经网络。该数据集统计了房价受到13个特征因素的影响,如图1所示。
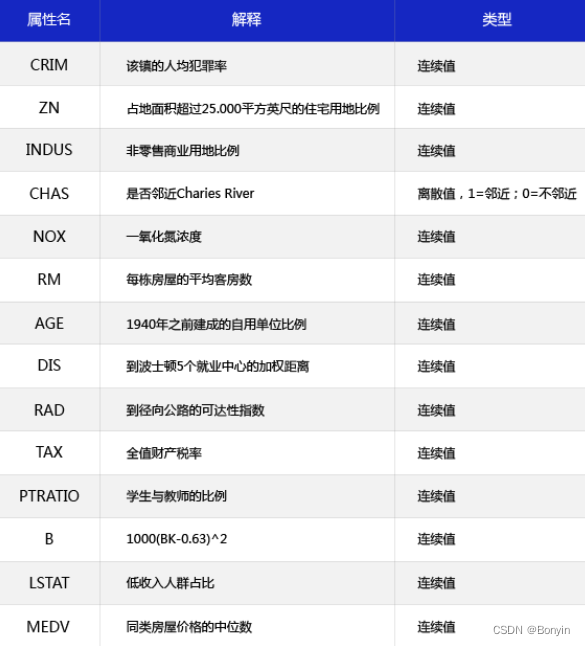 对于预测问题,可以根据预测输出的类型是连续的实数值,还是离散值,区分是回归还是分类问题。**因为房价是一个连续值,这是一个回归任务。**下面利用简单的线性回归来解决这个问题,并利用神经网络来实现这个模型。
对于预测问题,可以根据预测输出的类型是连续的实数值,还是离散值,区分是回归还是分类问题。**因为房价是一个连续值,这是一个回归任务。**下面利用简单的线性回归来解决这个问题,并利用神经网络来实现这个模型。
线性回归模型
假设房价和各个影像因素之间的函数关系是:
y=∑j=1Mxjwj+by= \sum_{j=1}^{M}x_jw_j + by=∑j=1Mxjwj+b
模型的目标就是通过拟合数据来求出wjw_jwj和bbb两个参数。线性回归模型采用均方误差MSE损失函数(LossLossLoss),用以衡量预测房价和真实值的差异,公式:
MSE=1N∑i=1N(Yi∧−Yi)2MSE=\frac{1}{N}\sum_{i=1}{N}(Y_i^{\wedge} - Y_i)^2MSE=N1∑i=1N(Yi∧−Yi)2
思考:为什么要以均方误差为损失函数?考虑到便于求解。
线性回归的神经网络结构
神经网络结构就是一个个神经元加层来组成。线性回归认为是神经网络模型的一种简单特例,是一个只有加权求和,没有非线性变换的神经元,如图2:。
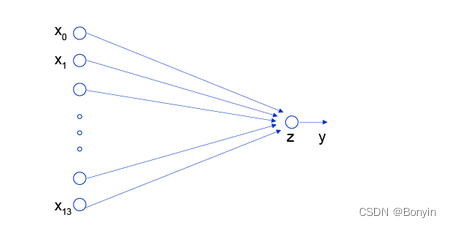
两层神经网络
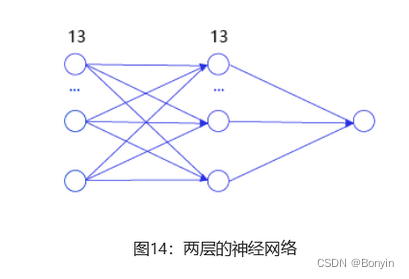
深度学习不仅实现了模型的端到端学习,还推动了人工智能进入工业大生产阶段,产生了标准化、自动化和模块化的通用框架。不同场景的深度学习模型具备一定的通用性,五个步骤即可完成模型的构建和训练。如图3所示。
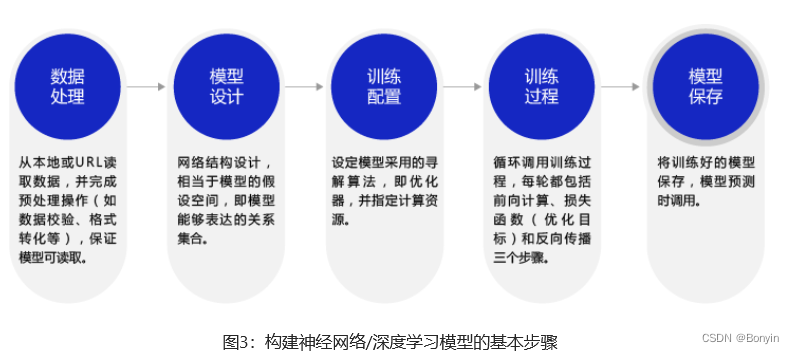 ### 数据处理
### 数据处理
数据探查
import numpy as np
import json
# 读入训练数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
- 数据变形
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
data = data.reshape([data.shape[0] // feature_num, feature_num])
print(data.shape) # 将数据做了转化样本总数是506个样本
- 划分数据集
将数据集划分训练集和测试集,训练集用于确定模型的参数,测试集用于评估模型的效果。图5:
 上学时总有一些自作聪明的同学,平时不认真学习,考试前临阵抱佛脚,将习题死记硬背下来,但是成绩往往并不好。因为学校期望学生掌握的是知识,而不仅仅是习题本身。另出新的考题,才能鼓励学生努力去掌握习题背后的原理。同样我们期望模型学习的是任务的本质规律,而不是训练数据本身,模型训练未使用的数据,才能更真实的评估模型的效果。
上学时总有一些自作聪明的同学,平时不认真学习,考试前临阵抱佛脚,将习题死记硬背下来,但是成绩往往并不好。因为学校期望学生掌握的是知识,而不仅仅是习题本身。另出新的考题,才能鼓励学生努力去掌握习题背后的原理。同样我们期望模型学习的是任务的本质规律,而不是训练数据本身,模型训练未使用的数据,才能更真实的评估模型的效果。
# 数据集划分操作
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
training_data.shape
# print(data.shape)
- 数据集归一化
利用最大值最小值归一方法,使得每个特征的值都是被缩放到[0,1]之间,这样做的好处有:1、模型训练更加高效,特征前的权重大小可以代表该变量对预测结果的贡献度。
maximums, minimums = \training_data.max(axis=0), \training_data.min(axis=0),
# 对数据进行归一化处理
for i in range(feature_num):data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
- 将上述过程封装为函数
def load_data():# 从文件导入数据datafile = './work/housing.data'data = np.fromfile(datafile, sep=' ')# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]feature_num = len(feature_names)# 将原始数据进行Reshape,变成[N, 14]这样的形状data = data.reshape([data.shape[0] // feature_num, feature_num])# 将原数据集拆分成训练集和测试集# 这里使用80%的数据做训练,20%的数据做测试# 测试集和训练集必须是没有交集的ratio = 0.8offset = int(data.shape[0] * ratio)training_data = data[:offset]# 计算训练集的最大值,最小值maximums, minimums = training_data.max(axis=0), \training_data.min(axis=0)# 对数据进行归一化处理for i in range(feature_num):data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])# 训练集和测试集的划分比例training_data = data[:offset]test_data = data[offset:]return training_data, test_data获取数据
# 获取数据
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:] # 实际值
模型设计
一层神经网络设计
模型的设计是深度学习模型关键要素之一,称为网络结构。相当于模型的假设空间,既是实现模型的“前向计算”(从输入到输出)过程。
如果将输入和输出都用向量表示,输入特征x有13个向量,y有1个向量。那么权重参数就是13*1。
w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0] #第一层的权重参数
w_t = np.array(w).reshape([13, 1]) # 相当于矩阵的转置
w_t.shape
# 一个特征列就是一个向量
假设第一个样本x[0]和一层神经网络进行运算。y=x.wTy=x.w^Ty=x.wT运算逻辑。其中x[0]=x1,x2,...x13x[0]={x_1,x_2,...x_{13}}x[0]=x1,x2,...x13,x [0]的shape是(1,13),wTw^TwT的维度是(13,1),刚好满足两个矩阵乘法的运算原则。
x1=x[0] #获取第一个样本
print(x1.shape)
t = np.dot(x1, w_t)
print(t.shape)
# 我们发现样本的特征向量与参数向量相乘的结果是scaler。
# 矩阵的乘法(1,13)(13,1) A*B其中A的列要和B的行相等才可进行矩阵的乘法运算。
b = -0.2
z = t + b
print(z)
完整的线性回归计算公式是:z=t+bz=t+bz=t+b,b是初始化偏移量,以上从特征[0]到计算输出值的过程就是“前向计算”。
定义一个类方便后面调用:
class MyNetwork(object):def __init__(self, num_of_weights):np.random.seed(0)self.w = np.random.randn(num_of_weights,1)self.b = 0.def forward_m(self,x):# 表示的是前向计算res = np.dot(x,self.w) +self.breturn res
二层神经网络
定义两层的神经网络,其中需要注意的地方:输入数据是直接和第一层进行x.wTx.w^Tx.wT运算,第一层每个神经元的输出则是做为第二层每个神经元的输入x。那么在第二层神经运算是w.xw.xw.x,就是对应位置元素相乘[x11.w11,x12.w12,x13.w13,...x113.w113][ x_1^1.w_1^1,x_1^2.w_1^2,x_1^3.w_1^3,...x_1^{13}.w_1^{13}][x11.w11,x12.w12,x13.w13,...x113.w113],在与第二层的权值参数w2w_2w2进行运算。
# 定义两层神经网络输出
class My2Network(object):def __init__(self, num_of_weights):np.random.seed(0)# 两层神经网络共享权值w self.w = np.random.randn(num_of_weights,1)self.ww = np.random.randn(num_of_weights,1)self.b = 0.def forword(self,x):# 前向计算有两层神经网络z_1 = np.dot(x,self.w)# 计算第一层输出做为第二层的输入out_1 = self.w.reshape([1,13]) * xz_2 = np.dot(out_1,self.ww)return z_1 + z_2 + self.b
训练配置
模型设计完成后,需要通过训练配置寻找模型的最优值,即通过损失函数来衡量模型的好坏。训练配置也是深度学习模型关键要素之一。
通过模型计算x1x_1x1表示的影响因素所对应的房价应该是z, 但实际数据告诉我们房价是y。这时我们需要有某种指标来衡量预测值z跟真实值y之间的差距。对于回归问题,最常采用的衡量方法是使用均方误差作为评价模型好坏的指标,公式为:
Loss=(y−z)2Loss = (y-z)^2Loss=(y−z)2
Loss就是损失函数,衡量模型好坏的指标。在回归问题中一般是均方误差作为损失函数,而在分类问题中采用交叉熵作为损失函数。
x1x_1x1样本的损失:
loss = (y_1 - res_1)*(y_1-res_1)
print(loss)
因为在计算损失函数需要把每个样本的损失函数得到,求和在平均。
Loss=1N∑i=1N(yi−zi)2Loss=\frac{1}{N}\sum_{i=1}^{N}(y_i - z_i)^2Loss=N1∑i=1N(yi−zi)2
在前Network类中增加loss函数。
class Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子np.random.seed(0)self.w = np.random.randn(num_of_weights, 1)self.b = 0.def forward(self, x):z = np.dot(x, self.w) + self.breturn zdef loss(self, z, y):error = z - ycost = error * errorcost = np.mean(cost)return cost
训练过程
在模型的前面两部完成,接下来就是求解参数w,bw,bw,b的数值,这就是模型训练的过程。求解w和b使得损失函数取得极小值。
eg.eg.eg. 下面给出一个微积分的案例:一个曲线在某点的导数。导数等于在该点处的切线的斜率。
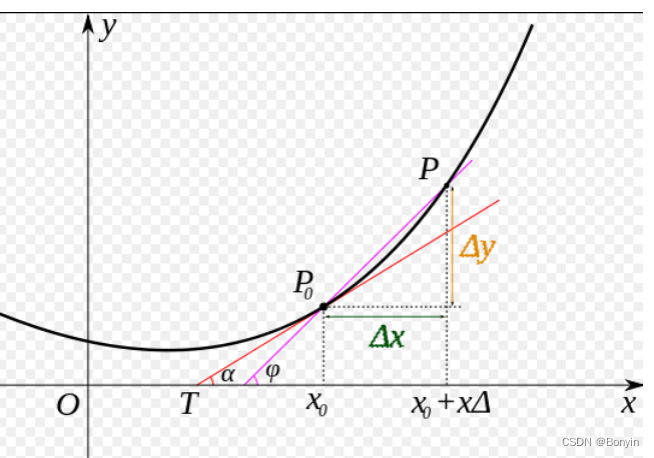
上图曲线在极值点处的斜率等于0,既是函数的极值点。那么损失函数的取值为下面方程组的解:
∂L∂w=0\frac{\partial L}{\partial w} = 0∂w∂L=0
∂L∂b=0\frac{\partial L}{\partial b} = 0∂b∂L=0
上述两个方程组的解就是最后模型训练获取到的参数。但是这种方法有个缺点:当模型中含有非线性变换,则不好计算。我们引入一种普世的方法——梯度下降法。
- 梯度下降算法
在现实中存在大量函数正向求解容易,但是反向求解不容易,被称为单向函数。神经网络的损失函数就是单向函数。
这种情况我们可以在现实生活中类比一个想从山峰走到山谷的盲人。他看不见山谷在哪儿(无法逆向求解损失函数为0时的参数值),但是可以伸出脚探索身边的坡度(当前点的导数,梯度)。所以求解Loss的最小值过程就是:在从当前参数取值,一步步按照梯度的反方向下降。直到到达最低点。
下面。我们随机从损失函数中去参数w5,w9w_5,w_9w5,w9看看他们的变化情况。
L=L(w5,w9)L=L(w_5,w_9)L=L(w5,w9)
我们将[w0,w1,...212][w_0,w_1,...2_{12}][w0,w1,...212]中除去w5,w9w_5,w_9w5,w9之前的参数和b全部固定下来。可以用图画出L(w5,w9)L(w_5,w_9)L(w5,w9)的形式。
net = Network(13)
losses = []
#只画出参数w5和w9在区间[-160, 160]的曲线部分,以及包含损失函数的极值
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros([len(w5), len(w9)])#计算设定区域内每个参数取值所对应的Loss
for i in range(len(w5)):for j in range(len(w9)):net.w[5] = w5[i]net.w[9] = w9[j]z = net.forward(x)loss = net.loss(z, y)losses[i, j] = loss#使用matplotlib将两个变量和对应的Loss作3D图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)w5, w9 = np.meshgrid(w5, w9)ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap='rainbow')
plt.show()
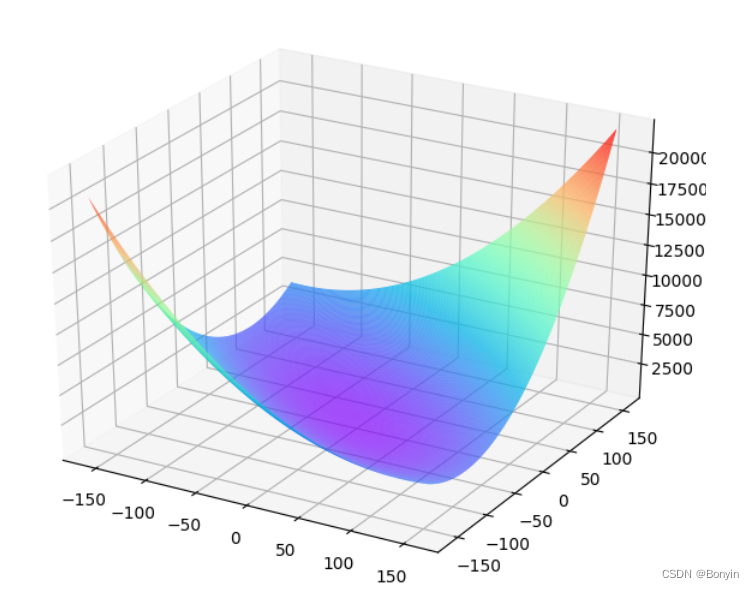 观察上述曲线呈现出“圆滑”的坡度,这正是我们选择以均方误差作为损失函数的原因之一。图6 呈现了只有一个参数维度时,均方误差和绝对值误差(只将每个样本的误差累加,不做平方处理)的损失函数曲线图。
观察上述曲线呈现出“圆滑”的坡度,这正是我们选择以均方误差作为损失函数的原因之一。图6 呈现了只有一个参数维度时,均方误差和绝对值误差(只将每个样本的误差累加,不做平方处理)的损失函数曲线图。
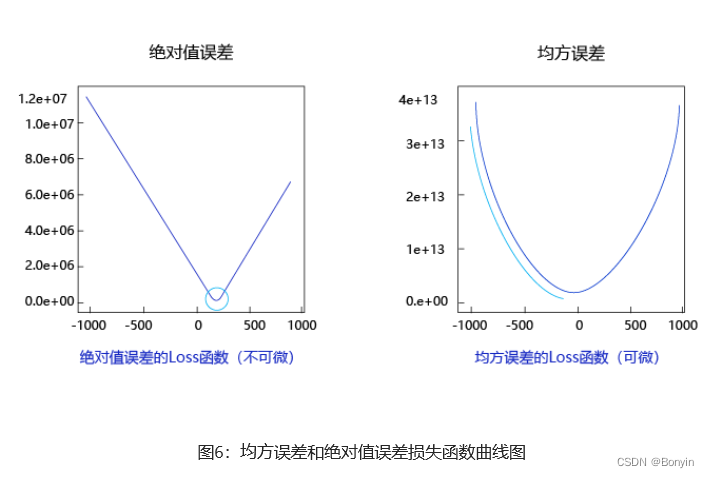 由此可见,均方误差表现的“圆滑”的坡度有两个好处:
由此可见,均方误差表现的“圆滑”的坡度有两个好处:
- 曲线在最低点出是可导的。
- 越接近最低点,曲线的坡度逐渐放缓,有助于通过当前的梯度来判断接近最低点的程度(是否逐渐减少步长,以免错过最佳点)。
然而绝对值误差事不具备的。这也是损失函数的设计不仅仅要考虑“合理性”,还要追求“易解性”的原因。
相关文章:

python实现波士顿房价预测
波士顿房价预测 目标 这是一个经典的机器学习回归场景,我们利用Python和numpy来实现神经网络。该数据集统计了房价受到13个特征因素的影响,如图1所示。 对于预测问题,可以根据预测输出的类型是连续的实数值,还是离散值ÿ…...

Pinia不酸,保甜
为什么是Pinia 怎么说呢,其实在过往的大部分项目里面,我并没有引入过状态管理相关的库来维护状态。因为大部分的业务项目相对来说比较独立,哪怕自身功能复杂的时候,可能也仅仅是通过技术栈自身的提供的状态管理能力来处理业务场景…...

uniapp生命周期
uniapp生命周期 uniapp生命周期不同于vue生命周期,uniapp生命周期分为: 应用生命周期 页面生命周期 组件生命周期 应用生命周期(官网) 注意 应用生命周期仅可在App.vue中监听,在其它页面监听无效。 onlaunch里进行页面跳转,如遇白…...
)
经典卷积模型回顾11—Xception实现图像分类(matlab)
Xception是一种深度卷积神经网络,它采用了分离卷积来实现深度神经网络的高准确性和高效率。Xception的名称来自“extreme inception”,意思是更加极致的Inception网络。 在传统的卷积神经网络中,每个卷积层都有若干个滤波器(即卷…...

移动App性能测试包含哪些内容?App性能测试工具有哪些?
随着互联网高科技的蓬勃发展,移动app的的需求量和供给量都较大。但一款好app的成功上线以及为用户带来高效体验,性能测试起着关键性的作用。性能测试是通过自动化的测试工具模拟多种正常、峰值以及异常负载条件来对系统的各项性能指标进行测试࿰…...

AI测试的迷思
近年来,我一直关注AI相关的测试,并积极参与多个全国性测试社区和社群。在这些社区中,我与不同公司和领域的测试专家交流探讨AI测试相关话题,包括业界顶尖公司的专家和国内知名测试学者。我也参加了多个大会,聆听了许多…...

[ 红队知识库 ] 一些常用bat文件集合
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...
Qt广告机服务器(上位机)
目录功能结构adSever.promain.cpptcp_MSG.h 共用Tcp传输信息adsever.h 服务器adsever.cpp 服务器addate.h 时间处理addate.cpp 时间处理adtcp.h 客户端Socket处理adtcp.cpp 客户端Socket处理client.h 客户端信息类client.cpp 客户端信息类admsglist.h 信息记录模块admsglist.cp…...

SOA架构的理解
1. SOA概述 SOA(Service-Oriented Architecture,面向服务的架构)是一种在计算机环境中设计、开发、部署和管理离散模型的方法。SOA不是一种新鲜事物,它是在企业内部IT系统重复构建以及效率低下的背景下提出的。在SOA模型中&#x…...
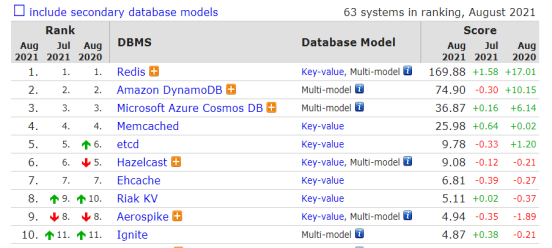
如何选择一款数据库?
1主流数据库技术介绍常见的数据库模型主要分为SQL关系型数据库和NoSQL非关系型数据库。其中关系型数据库分为传统关系数据库和大数据数据库,非关系型数据库分为键值存储数据库、列存储数据库、面向文档数据库、图形数据库、时序数据库、搜索引擎存储数据库及其他&am…...

week2
蓝桥2 递归*树的遍历约数之和分形之城并查集亲戚连通块中点的数量*食物链银河英雄传说哈希笨拙的手指模拟散列表单调队列剪裁序列滑动窗口最大子序和KMP周期递归 *树的遍历 中序遍历: 遍历左子树,根节点,右子树 后序遍历:遍历左子树,右子树,根节点 一个二叉树,树中每个…...

JavaScript的学习
一、引言 1.1 JavaScript简介 JavaScript一种解释性脚本语言,是一种动态类型、弱类型、基于原型继承的语言,内置支持类型。它的解释器被称为JavaScript引擎,作为浏览器的一部分,广泛用于客户端的脚本语言,用来给HTML网…...

用gin写简单的crud后端API接口
提要使用gin框架(go的web框架)来创建简单的几个crud接口)使用技术: gin sqlite3 sqlx创建初始工程新建文件夹,创建三个子文件夹分别初始化工程 go mod如果没有.go文件,执行go mod tidy可能报错(warning: "all" matched no packages), 可以先不弄,只初始化模块就行(…...
)
CF大陆斗C战士(三)
文章目录[C. Good Subarrays](https://codeforces.com/problemset/problem/1398/C)题目大意题目分析code[C. Boboniu and Bit Operations](https://codeforces.com/problemset/problem/1395/C)题目大意题目分析code[C. Rings](https://codeforces.com/problemset/problem/1562/…...

TTS | 语音合成论文概述
综述系列2021_A Survey on Neural Speech Synthesis论文:2106.15561.pdf (arxiv.org)论文从两个方面对神经语音合成领域的发展现状进行了梳理总结(逻辑框架如图1所示):核心模块:分别从文本分析(textanalysi…...

HTML第5天 HTML新标签与特性
新标签与特性文档类型设定前端复习帮手W3Schoool常用新标签datalist标签,与input元素配合,定义选项列表fieldset元素新增input表单文档类型设定 document – HTML: 开发环境输入html:4s – XHTML: 开发环境输入html:xt – HTML5: 开发环境输入html:5 前…...

java ee 之进程
目录 1.进程的概念 2.进程管理 3.进程属性(pcb) 3.1pid 3.2内存指针 3.3文件描述符 3.4进程调度 3.4.1进程状态 3.4.2 进程的优先级 3.4.3进程的上下文 3.4.4进程的记账信息 5.进程间通信 1.进程的概念 一个运行起来的程序,就是进程 .exe是一个可执行文件(程序),双…...

Linux学习记录——십사 进程控制(1)
文章目录1、进程创建1、fork函数2、进程终止1、情况分类2、如何理解进程终止3、进程终止的方式3、进程等待1、进程创建 1、fork函数 fork函数从已存在进程中创建一个新进程,新进程为子进程,原进程为父进程。 #include <unistd.h> pid_t fork(vo…...

使用 create-react-app 脚手架搭建React项目
❀官网 1、安装脚手架:npm install -g create-react-app 2、查看版本:create-react-app -V !!!注意 Node版本必须是14以上,不然会报以下错误。 3、创建react项目(项目名不能包含大写字母&…...
inquirerjs
inquirerjs inquirerjs是一个用来实现命令行交互界面的工具集合。它帮助我们实现与用户的交互交流,比如给用户一个提醒,用户给我们一个答案,我们根据用户的答案来做一些事情,典型应用如plop等生成器工具。 npm install inquirer…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
