数据结构3——线性表2:线性表的顺序结构
顺序结构的基本理解
定义:
把逻辑上相邻的数据元素存储在物理上相邻(占用一片连续的存储单元,中间不能空出来)的存储单元的存储结构

存储位置计算:
LOC(a(i+1))=LOC(a(i))+lLOC(a(i+1))=LOC(a(i))+l LOC(a(i+1))=LOC(a(i))+l
LOC(a(i))=LOC(a(j))+(i−j)lLOC(a(i))=LOC(a(j))+(i-j)l LOC(a(i))=LOC(a(j))+(i−j)l
其中lll为每个元素所需要占用的存储单元
顺序表的优点:
以物理位置相邻表示逻辑关系,任意元素均可随机存取
顺序表的顺序存储表示:
【地址连续、依次存放、随机存取、类型相同】==>数组(元素)
所以我们可以用一维数组来表示顺序表。但是顺序表长是可以变化的;而数组长度是不可变的,所以我们会额外使用一个变量来表示当前位置在顺序表中的长度
# define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
typedef struct{ ElemType elem[LIST_INIT_SIZE]; int lenth; //当前长度
}SqList
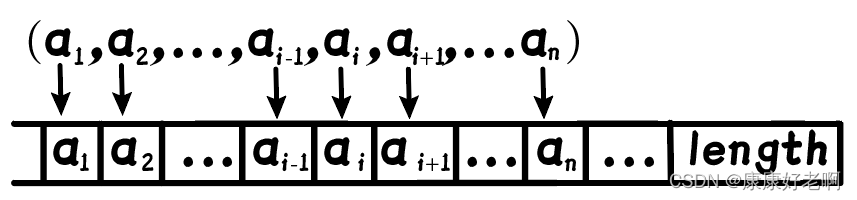
注意:逻辑位序和物理位序相差1(因为数组第一项是a[0])
例子:多项式的顺序存储结构类型定义
P(x)=Axa+Bxb+Cxc+⋅⋅⋅+Z(i)xzP(x)=Ax^a+Bx^b+Cx^c+···+Z(i)x^z P(x)=Axa+Bxb+Cxc+⋅⋅⋅+Z(i)xz
其线性表为
P=((A,a),(B,b),(C,c),...,(Z,z))P = ( ( A , a ) , ( B , b ) , ( C , c ) , . . . , ( Z , z ) ) P=((A,a),(B,b),(C,c),...,(Z,z))
# define MAXSIZE 1000
typedef struct{ //多项式非零项的意义 float p; //系数 int e; //指数
}Polynomial;
typedef struct{ Polynomial *elem; //存储空间的基地址 int length; //多项式中当前项的系数
}SqList; //多项式的顺序存储结构类型为SqList
补充
补充1:数组静态与动态的区别
| 数组静态分配 | 数组动态分配 |
|---|---|
| typedef struct{ | typedef struct{ |
| ElemType data[maxsize]; | **ElemType *data; ** |
| int length; | int length; |
| }SqList;//顺序表类型 | }SqList;//顺序表类型 |
在数组的静态分配中,data[maxsize]本质上存储的是data[0]的地址;而*data这个指针存储的也是地址,本质上相同。而数组动态分配是由申请储存空间完成的:
SqList L;
L.data = (ElemType*)malloc(sizeof(ElemType)×Maxsize)
补充2:常用函数
需要加载头文件:<stdlib.h>
malloc(m)函数:开辟m字节长度的地址空间,并返回这段空间的首地址
sizeof(x)运算:计算变量x的长度
free§函数:释放指针p所指变量的存储空间,即彻底删除一个变量
(ElemType*)malloc···:强制转换类型方法
补充3:a与b的交换问题
引用类型做参数(C++):
int i=5;
int &j=i;
j是一个引用类型,i的值改变的时候,j的值也会随之发生变化
比如交换a,b的函数,可以有如下两种方式:
| 利用指针类型 | 利用引用类型 |
| ----------------------------- | --------------------------- |
| #include <iostream.h> | #include <iostream.h> |
| void swap(float *m,float *n){ | void swap(float&m,float&n){ |
| float temp; | float temp; |
| temp = *m; | temp=m; |
| *m = *n; | m=n; |
| *n = temp; | n=temp; |
| } | } |
| void main(){ | void main(){ |
| float a,b, *p1, *p2; | float a,b; |
| cin>>a>>b; | cin>>a>>b; |
| p1=&a; p2=&b; | swap(a,b); |
| swap(p1,p2); | count<<a<<endl<<b<<endl; |
| count<<a<<endl<<b<<endl; | } |
| } | |
补充4:宏定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
补充5:内存相关
| 软件 | C | C++ |
|---|---|---|
| 获取内存 | malloc | new |
| 释放内存 | free | delete |
基本操作的实现
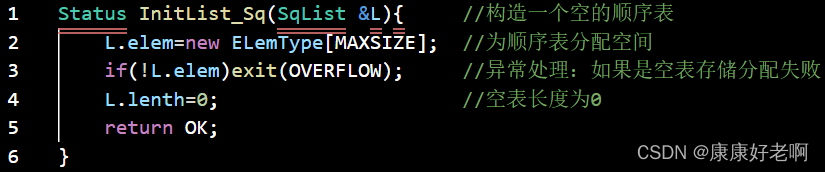
线性表初始化:InitList(&L)
操作结果:构造一个空的线性表L
C++:
C:
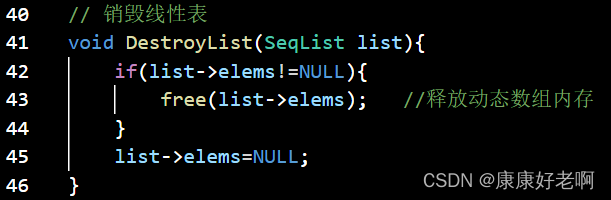
线性表销毁:DestoryList(&L)
初始条件:线性表L已经存在
操作结果:销毁线性表L
C++:

C:
C(1):

线性表清空:ClearList(&L)
初始条件:线性表L已经存在
操作结果:将线性表L重置为空表
C++:

C:

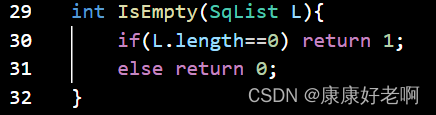
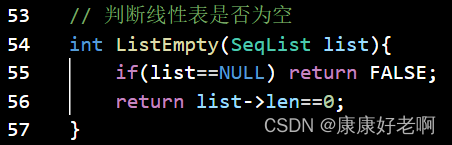
线性表清空判断:ListEmpty(L)
初始条件:线性表L已经存在
操作结果:若线性表L为空表,则返回TRUE;否则返回FALSE
C++:
C:
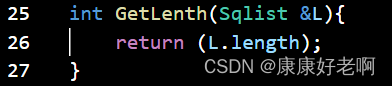
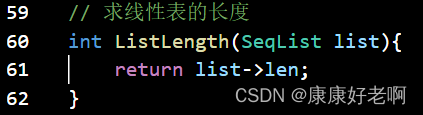
线性表长度:ListLength(L)
初始条件:线性表L已经存在
操作结果:返回线性表L中的数据元素个数
C++:
C:
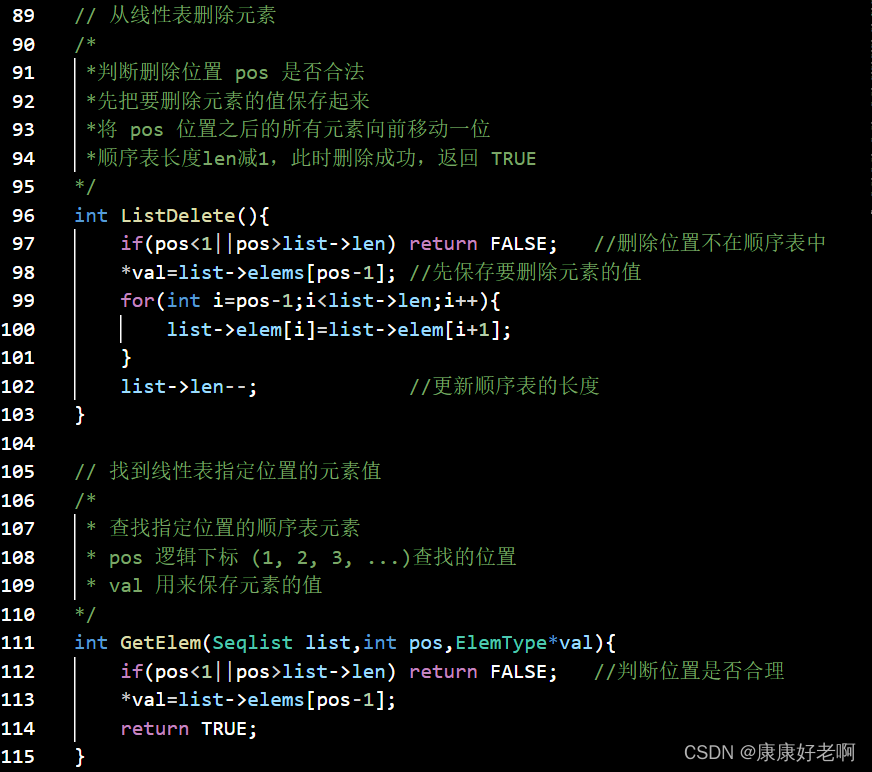
线性表查找:GetElem(L,i,&e)
初始条件:线性表L已经存在,1≤i≤ListLength(L)
操作结果:用e返回线性表L中第i个数据元素的值
C++:

C:

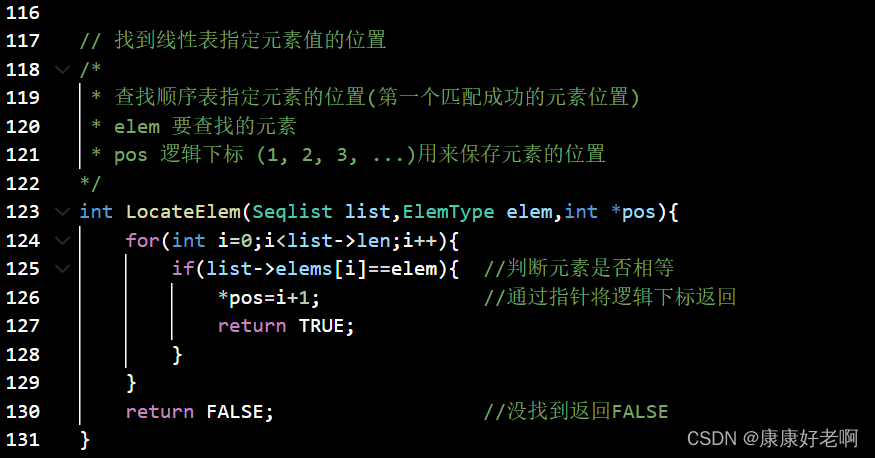
线性表定位:LocateElem(L,e,compare())
**初始条件:**线性表L已经存在,compare()是数据元素的判定函数
**操作结果:**返回L中第1个与e满足compare()的数据元素的位序。这样的元素不存在则返回值为0
C++:
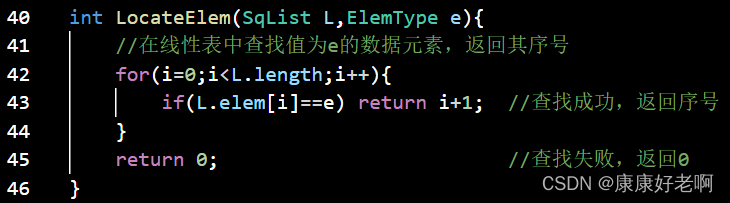
C:
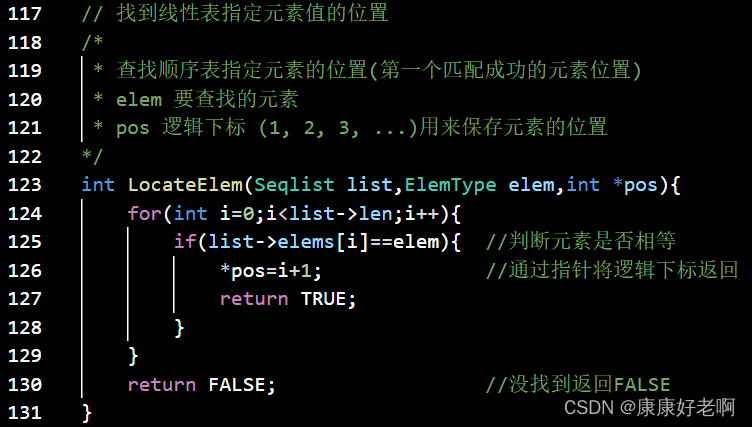
算法分析:
频度(平均查找长度为)期望值为
(1+2+3+4+5+6+⋅⋅⋅+n−1+n)/n=(n+1)/2(1+2+3+4+5+6+···+n-1+n)/n=(n+1)/2 (1+2+3+4+5+6+⋅⋅⋅+n−1+n)/n=(n+1)/2
拓展一下:
上图的情况就是当查找概率都相等时的结果。
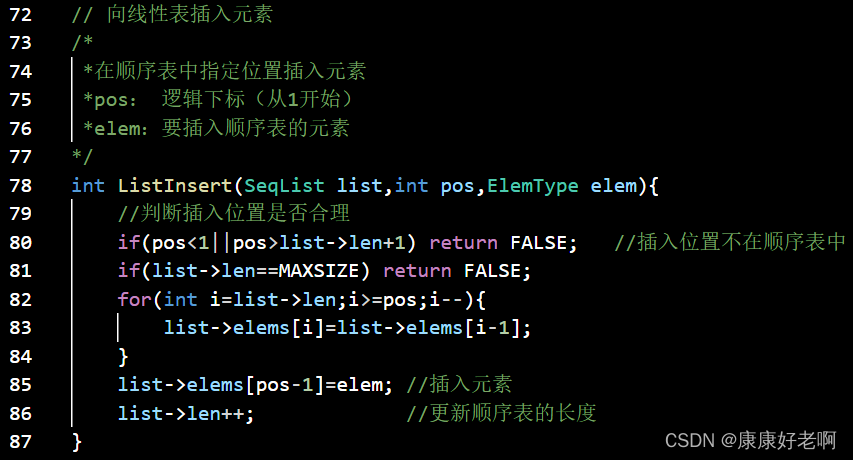
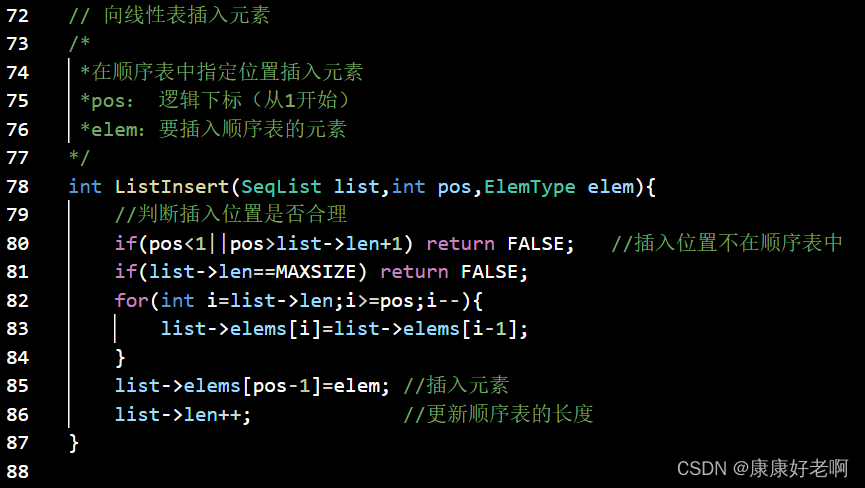
线性表元素插入:ListInsert(&L,i,e)
初始条件:线性表L已经存在,1≤i≤ListLength(L)+1
操作结果:在L的第i个位置插入新的数据元素e,L的长度加一
算法思想:
1)判断插入位置i是否合法。
2)判断顺序表的存储空间是否已满,若已经满了返回ERROR
C:
算法分析:
插入的位置有如下三种情况:
① 插在位置最后,则根本不需要移动,速度较快
② 插在位置中间,则需要移动一定数量的元素,速度适中
③ 插在位置最前,则需要将表中所有元素后移,速度很慢
那么平均的情况如何?
我们知道总共有n+1个插入位置,第i个插入位置需要移动n-i+1次,则
(1+2+3+4+5+6+⋅⋅⋅+n−1+n)/(n+1)=n/2(1+2+3+4+5+6+···+n-1+n)/(n+1)=n/2 (1+2+3+4+5+6+⋅⋅⋅+n−1+n)/(n+1)=n/2
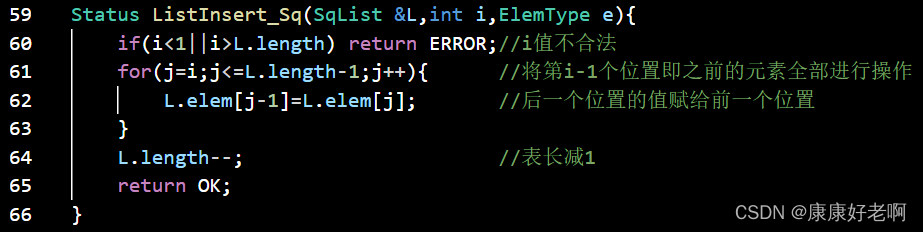
线性表元素删除:ListDelete(&L,i,&e)
初始条件:线性表L已经存在,1≤i≤ListLength(L)
操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减一
算法思想:
① 判断删除位置i是否合法(合法值1≤i≤n)
② 将欲删除的元素保留在e中
③ 将第i+1至第n位的元素依次向前移动一个位置
④ 表长减1,删除成功返回OK
C++:
C:
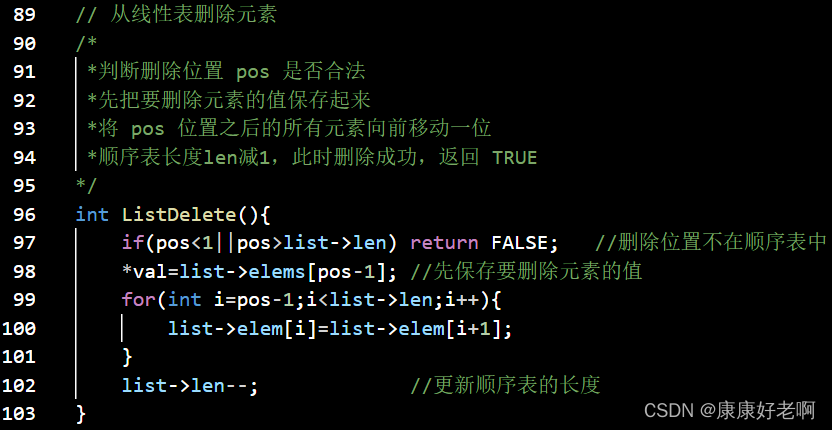
算法分析:此处的分析与线性表元素的插入十分类似,
(1+2+3+4+5+6+⋅⋅⋅+n−1)/n=(n−1)/2(1+2+3+4+5+6+···+n-1)/n=(n-1)/2 (1+2+3+4+5+6+⋅⋅⋅+n−1)/n=(n−1)/2
顺序表总结:
优点:
· 存储密度大(结点本身所占储存量/结点结构所占存储量)
· 可以随机存取表中任意元素
缺点:
· 插入删除某元素时需要移动大量元素
· 浪费存储空间
· 属于静态存储形式,数据元素不能自由扩充
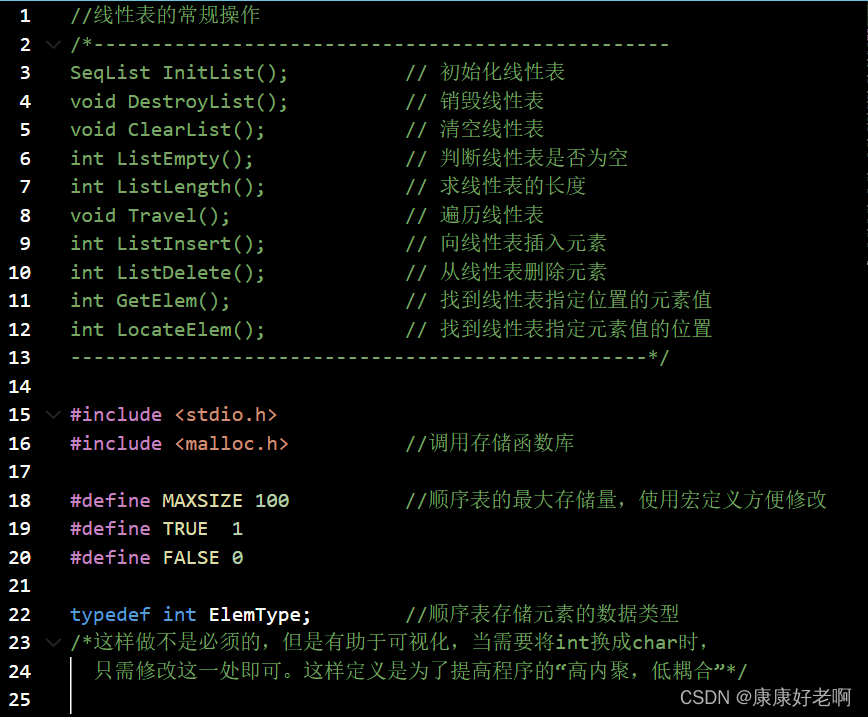
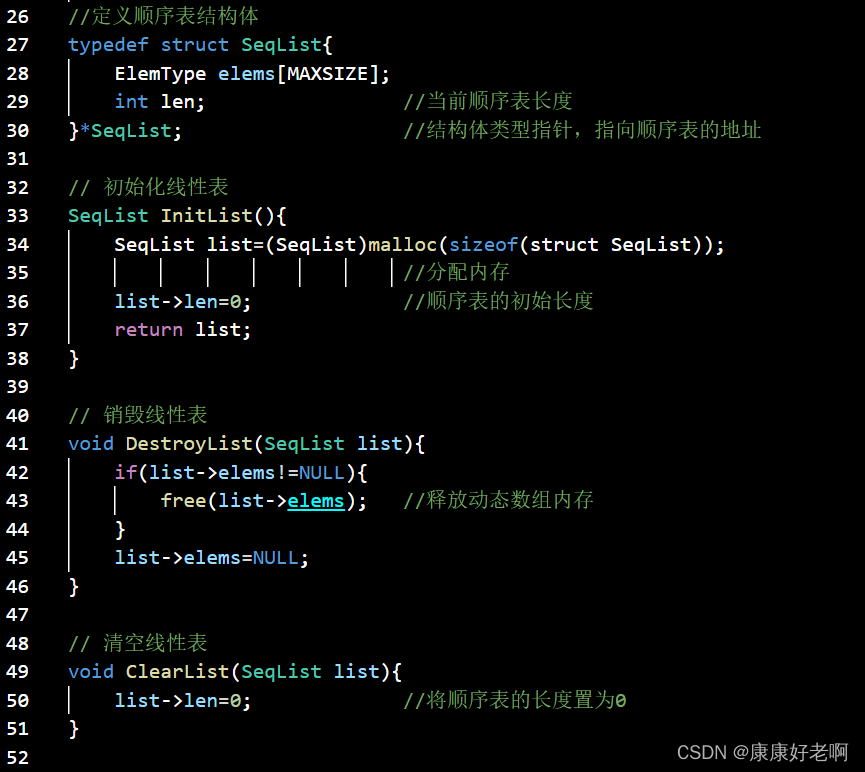
附录:顺序表完整C源码

相关文章:

数据结构3——线性表2:线性表的顺序结构
顺序结构的基本理解 定义: 把逻辑上相邻的数据元素存储在物理上相邻(占用一片连续的存储单元,中间不能空出来)的存储单元的存储结构 存储位置计算: LOC(a(i1))LOC(a(i))lLOC(a(i1))LOC(a(i))l LOC(a(i1))LOC(a(i))l L…...
VMware虚拟机搭建环境通用方法
目录一、前期准备1.下载并安装一个虚拟机软件二、开始创建虚拟机1.配置虚拟机硬件相关操作2.虚拟机网络相关操作三、开机配置相关内容0.开机遇到报错处理(选看--开机没有报错请忽略)1.开始配置2.开机之后配置3.使用xshell远程登录4.使用xshell配置虚拟机…...

2.Fully Convolutional Networks for Semantic Segmentation论文记录
欢迎访问个人网络日志🌹🌹知行空间🌹🌹 文章目录1.基础介绍2.分类网络转换成全卷积分割网络3.转置卷积进行上采样4.特征融合5.一个pytorch源码实现参考资料1.基础介绍 论文:Fully Convolutional Networks for Semantic Segmentati…...

深度解析Spring Boot自动装配原理
废话不多说了,直接来看源码。源码解析SpringBootApplication我们在使用idea创建好Spring Boot项目时,会发现在启动类上添加了SpringBootApplication注解,这个注解就是Spring Boot的核心所在。点击注解可以查看到到它的实现ementType.TYPE) Re…...

Linux:环境变量
目录一、环境变量的理解(1)什么是环境变量?(2)Linux中的环境变量二、环境变量的使用(1)PATH环境变量(2)和变量相关的指令三、环境变量与普通变量的区别在平时使用电脑的时…...

Codeforces Round 703 (Div. 2)(A~D)
A. Shifting Stacks给出一个数组,每次可以将一个位置-1,右侧相邻位置1,判断是否可以经过若干次操作后使得数列严格递增。思路:对于每个位置,前缀和必须都大于该位置应该有的最少数字,即第一个位置最少是0&a…...

Django项目5——基于tensorflow serving部署深度模型——windows版本
1:安装docker for windows 可能需要安装WLS2,用于支持Linux系统,参照上面的教程安装 2:在Powershell下使用docker docker pull tensorflow/serving3:在Powershell下启动tensorflow serving docker run -p 8500:8500 …...
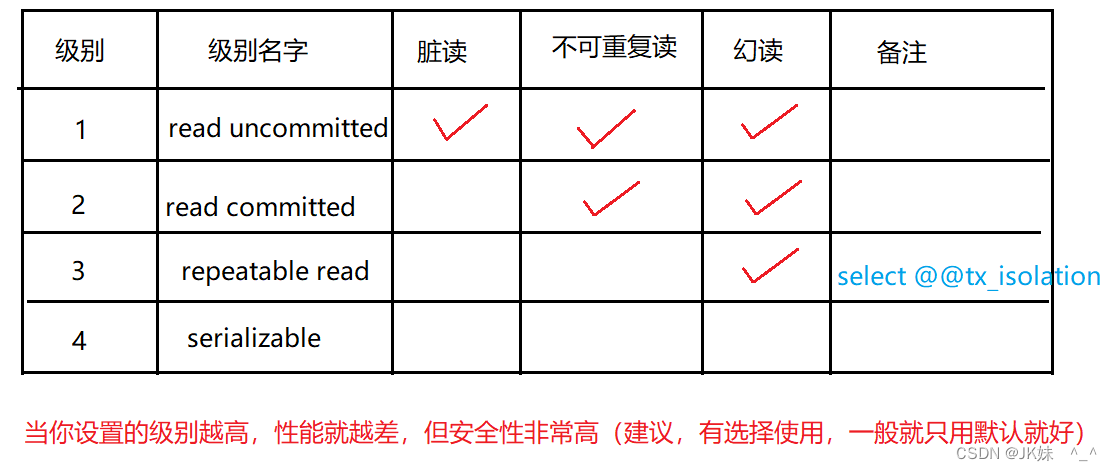
MySQL基础篇3
第一章 多表关系实战 1.1 实战1:省和市 方案1:多张表,一对多 方案2:一张表,自关联一对多 id1 name‘北京’ p_id null; id2 name‘昌平’ p_id1 id3 name‘大兴’ p_id1 id3 name‘上海’ p_idnull id4 name‘浦东’…...
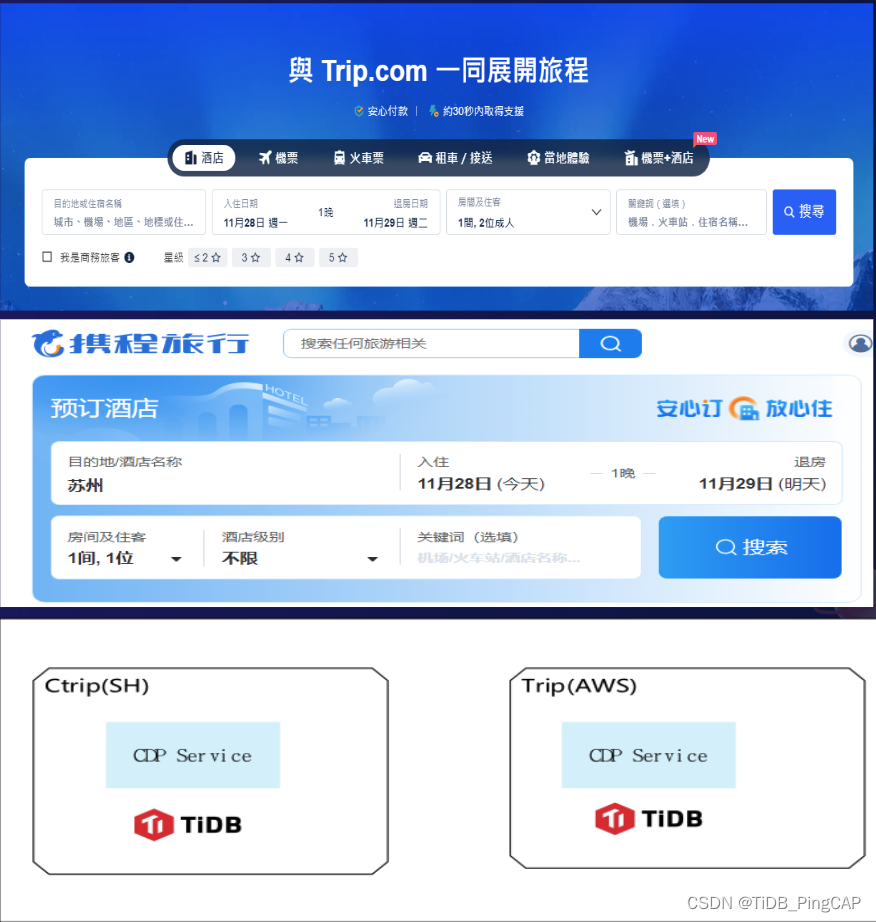
携程 x TiDB丨应对全球业务海量数据增长,一栈式 HTAP 实现架构革新
随着新冠病毒疫情的缓解和控制,全球旅游业逐渐开始重新复苏。尤其在一些度假胜地,游客数量已经恢复到疫情前的水平。 携程作为全球领先的一站式旅行平台,旗下拥有携程旅行网、去哪儿网、Skyscanner 等品牌。携程旅行网向超过 9000 万会员提供…...

记一次Kafka warning排查过程
1、前因 在配合测试某个需求的时候,正好看到控制台打印了个报错,如下: 2023-03-06 17:05:58,565[325651ms][pool-28-thread-1][org.apache.kafka.common.utils.AppInfoParser][WARN] - Error registering AppInfo mbean javax.management.I…...
)
MySQL学习笔记(6.视图)
1. 视图作用 (1). 简化业务,将多个复杂条件,改为视图 (2). mysql对用户授权,只能控制表权限,通过视图可以控制用户字段权限。 (3). 可以避免基本表变更,影响业务。只需更改视图即可。 2. 视图(创建&…...

java多线程与线程池-01多线程知识复习
多线程知识复习 文章目录 多线程知识复习第1章 多线程基础1.1.2 线程与进程的关系1.2 多线程启动1.2.1 线程标识1.2.2 Thread与Runnable1.2.3 run()与start()1.2.4 Thread源码分析1.3 线程状态1.3.1 NEW状态1.3.2 RUNNABLE状态1.3.3 BLOCKED状态1.3.4 WAITING状态1…...

Typescript - 将命名空间A导入另一个命名空间B作为B的子命名空间,并全局暴露命名空间B
前言 最近相统一管理 ts 中的类型声明,这就需要将各模块下的命名空间整合到全局的命名空间下,牵涉到从别的文件中引入命名空间并作为子命名空间在全局命名空间中统一暴露。 将命名空间A导入另一个命名空间B作为B的子命名空间 文件说明 assets.ts 文件中…...
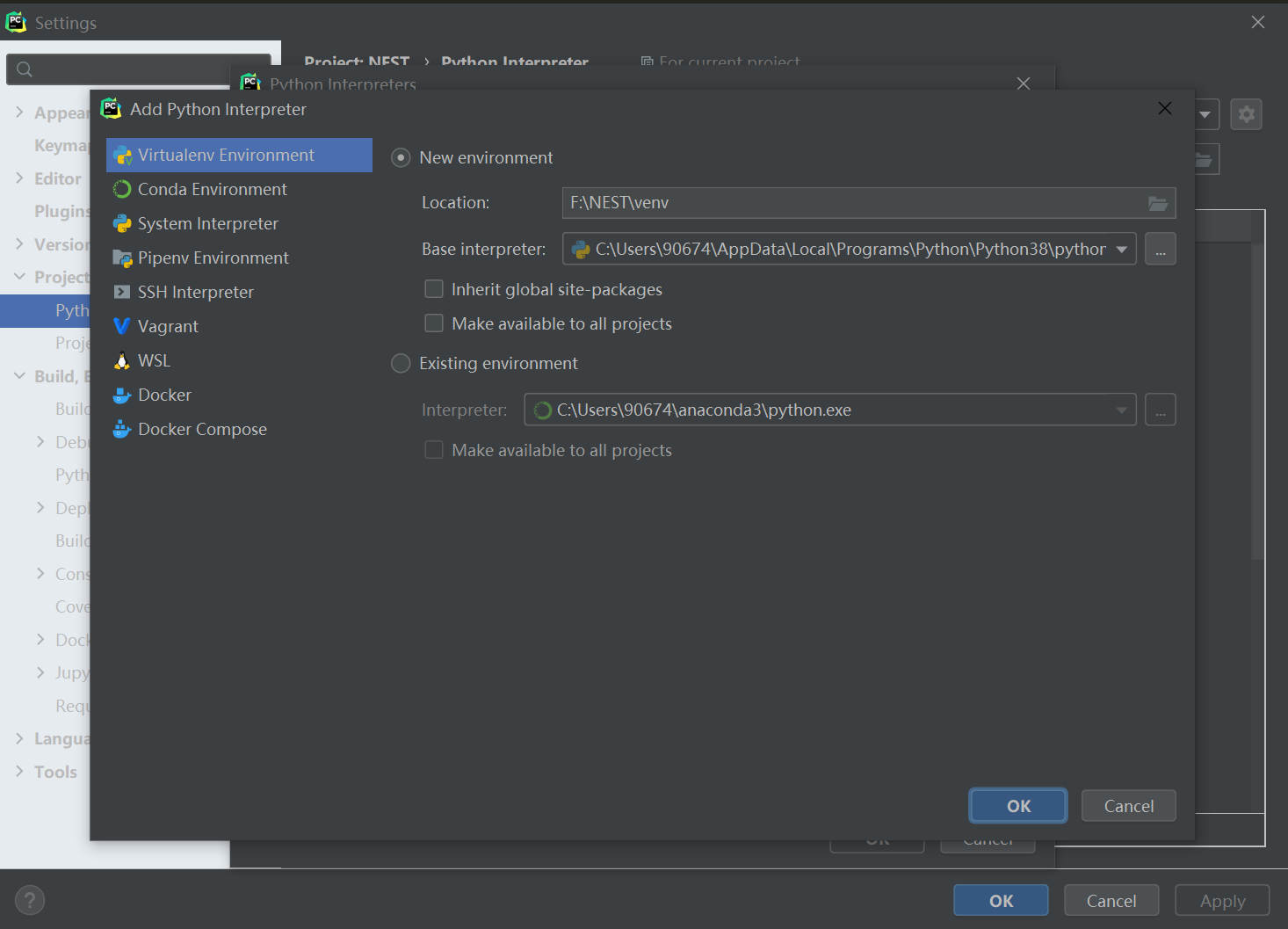
Windows下实现Linux内核的Python开发(WSL2+Conda+Pycharm)
许多软件可以通过Python交互,但没有开发Windows版本,这个时候装双系统或虚拟机都很不方便,可以采取WSL2CondaPycharm的策略来进行基于Linux内核的Python开发。启动WSL2,安装Linux内核教程:旧版 WSL 的手动安装步骤 | M…...

新闻发布网站分析及适用场景
在当今数字时代,发布新闻的渠道已经不再局限于传统媒体,越来越多的企业、组织和个人开始使用互联网平台发布新闻稿,以提升品牌知名度和影响力。本文将介绍一些可以发布新闻的网站,并分析其特点和适用场景。一、新闻稿发布平台1.新…...
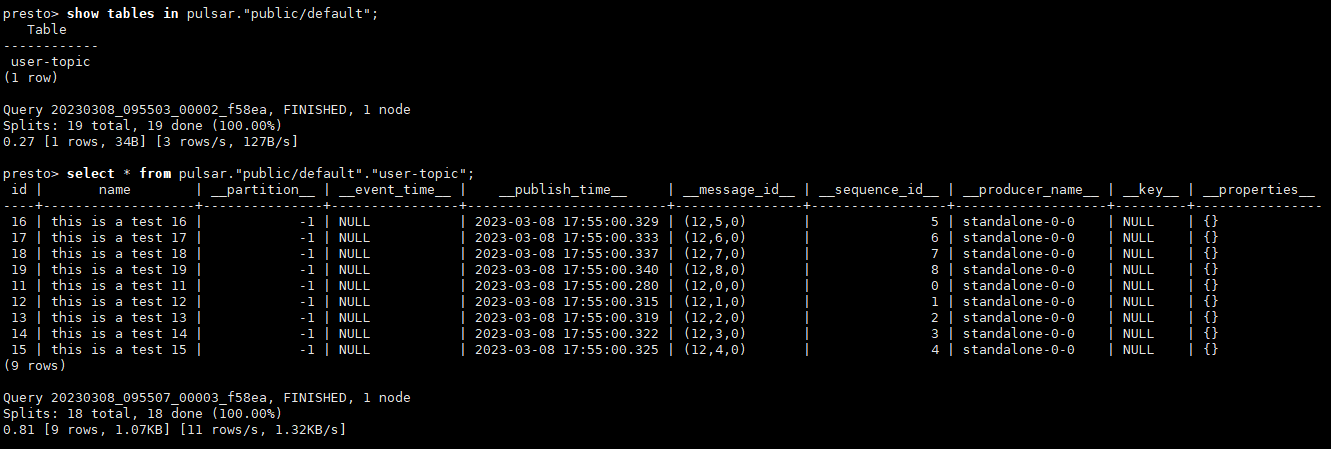
云原生时代顶流消息中间件Apache Pulsar部署实操之Pulsar IO与Pulsar SQL
文章目录Pulsar IO (Connector连接器)基础定义安装Pulsar和内置连接器连接Pulsar到Cassandra安装cassandra集群配置Cassandra接收器创建Cassandra Sink验证Cassandra Sink结果删除Cassandra Sink连接Pulsar到PostgreSQL安装PostgreSQL集群配置JDBC接收器创建JDBC Sink验证JDBC …...
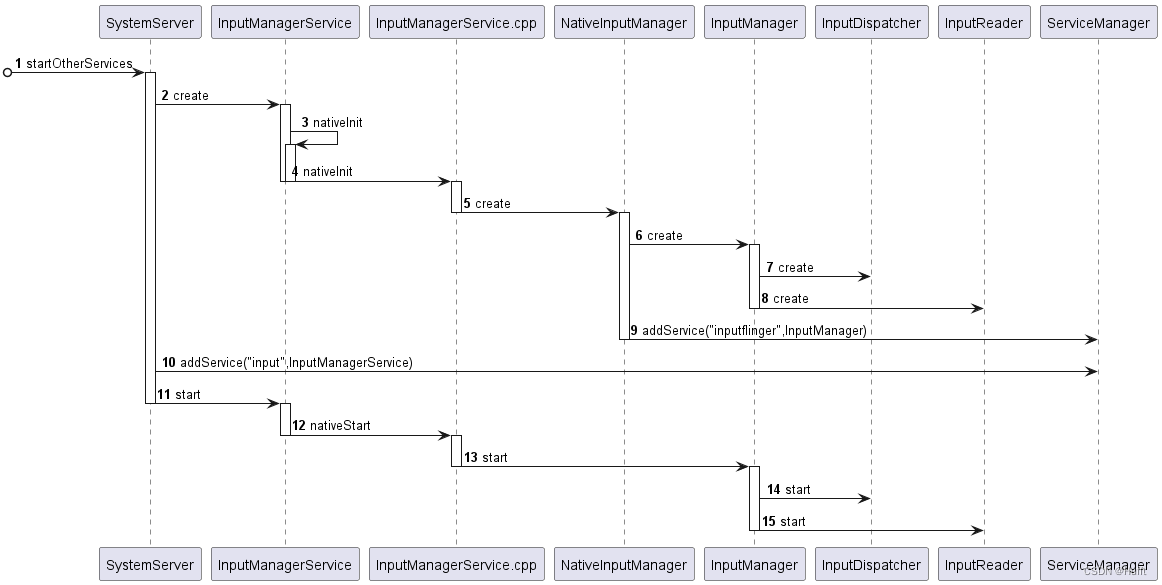
Input子系统(一)启动篇
代码路径 基于AndroidS(12.0)代码 system/core/libutils/Threads.cppframeworks/base/services- java/com/android/server/SystemServer.java- core- java/com/android/server/input/InputManagerService.java- jni/com_android_server_input_InputMan…...

WuThreat身份安全云-TVD每日漏洞情报-2023-03-08
漏洞名称:Agilebio Lab Collector 远程命令执行 漏洞级别:高危 漏洞编号:CVE-2023-24217,CNNVD-202303-375 相关涉及:Agilebio Lab Collector 4.234 漏洞状态:EXP 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-05536 漏洞名称:PrestaShop “Xen Forum”模…...

ABP IStringLocalizer部分场景不生效的问题
问题描述: 本地项目依赖注入本地化服务时候生效,第三方项目调用本地接口时候出现本地化失效的问题。 解决方案: 第三方服务封装的 GetHttp 请求的请求头中添加 语言相关信息 request.Headers.Add("accept-language", "zh-C…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

