1947抓住那头牛(队列 广度优先搜索)
目录
题目描述
解析
解题思路
代码部分
代码部分
运行结果
看看len数组中各个位置的标记值
为什么这样做一定是最短路径:
题目描述
农夫知道一头牛的位置,想要抓住它。农夫和牛都位于数轴上,农夫起始位于点N(0<=N<=100000),牛位于点K(0<=K<=100000)。农夫有两种移动方式:
1.从X移动到X-1或X+1,每次移动花费一分钟
2.从X移动到2*X,每次移动花费一分钟假设牛没有意识到农夫的行动,站在原地不动。
农夫最少要花多少时间才能抓住牛?
输入
两个整数,N和K。
输出
一个整数,农夫抓到牛所要花费的最小分钟数。
样例输入:
5 17样例输出:
4解析
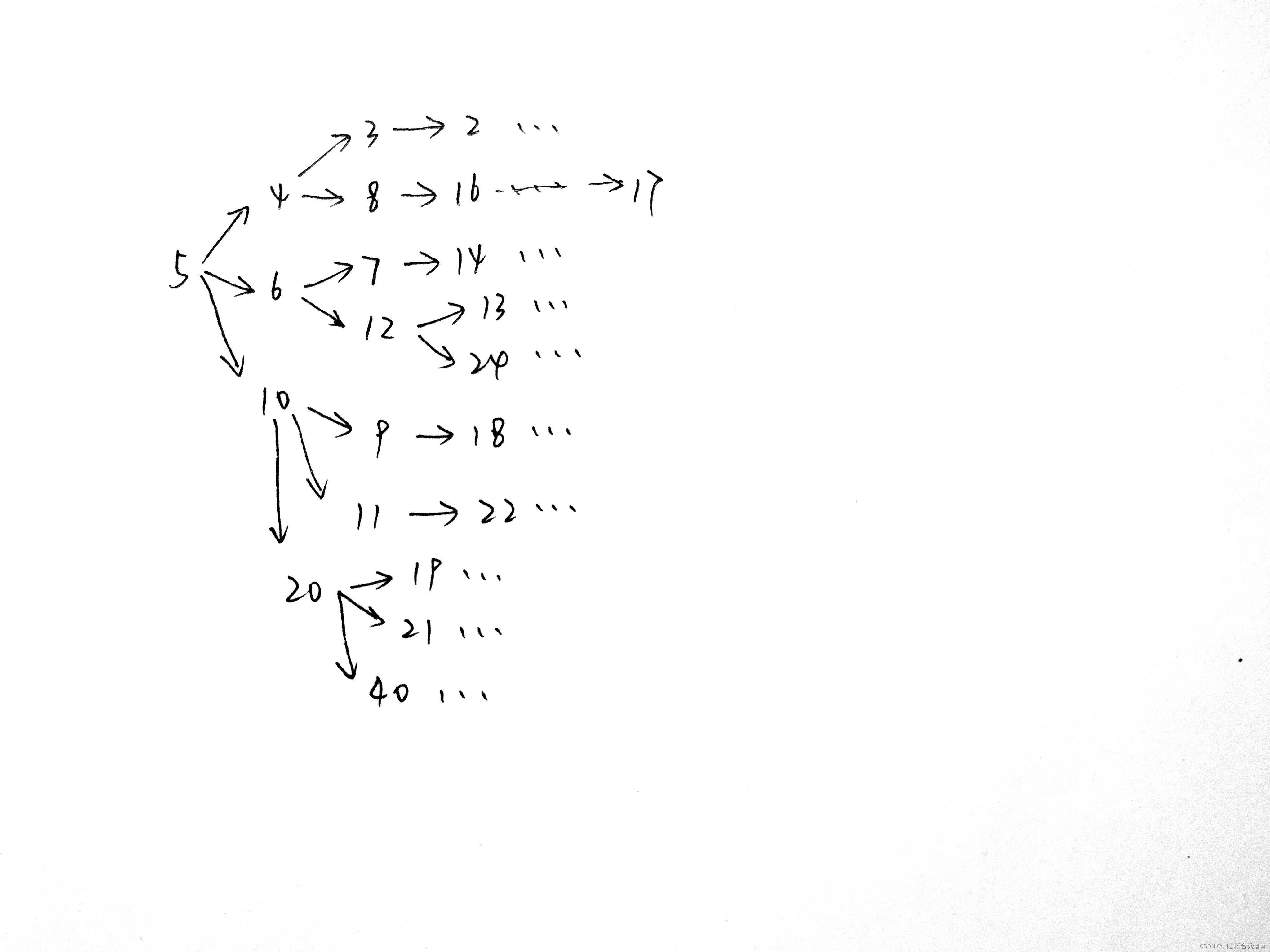
使用队列:
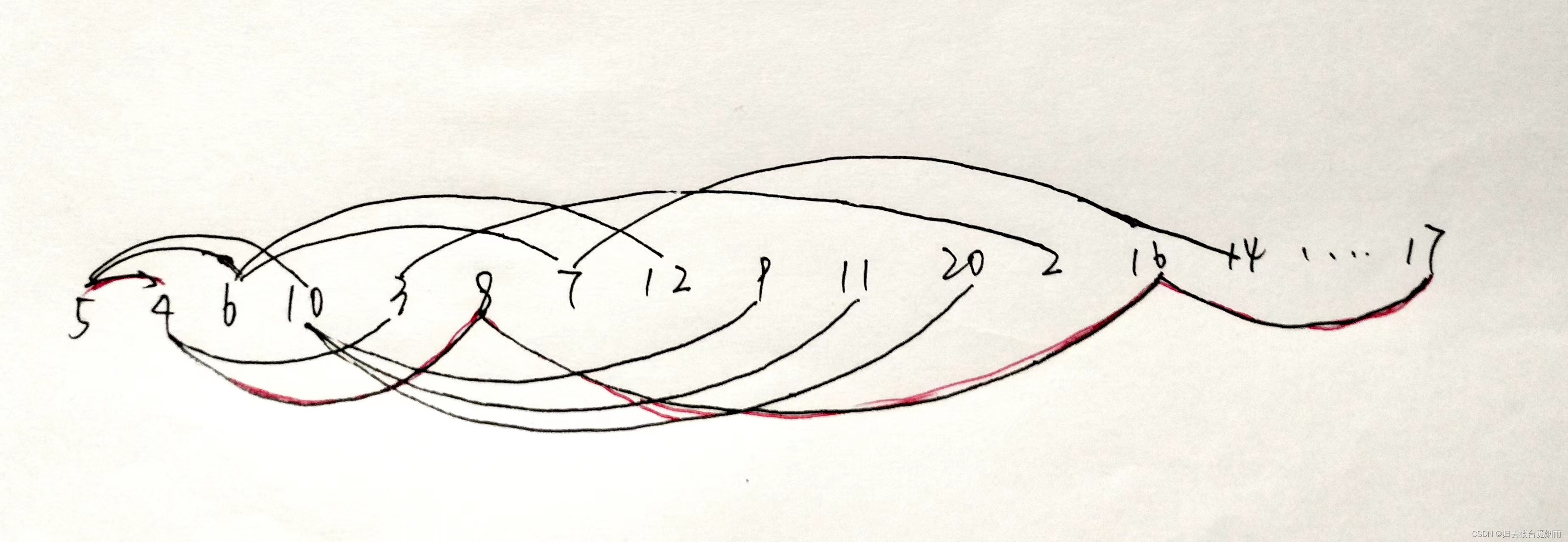
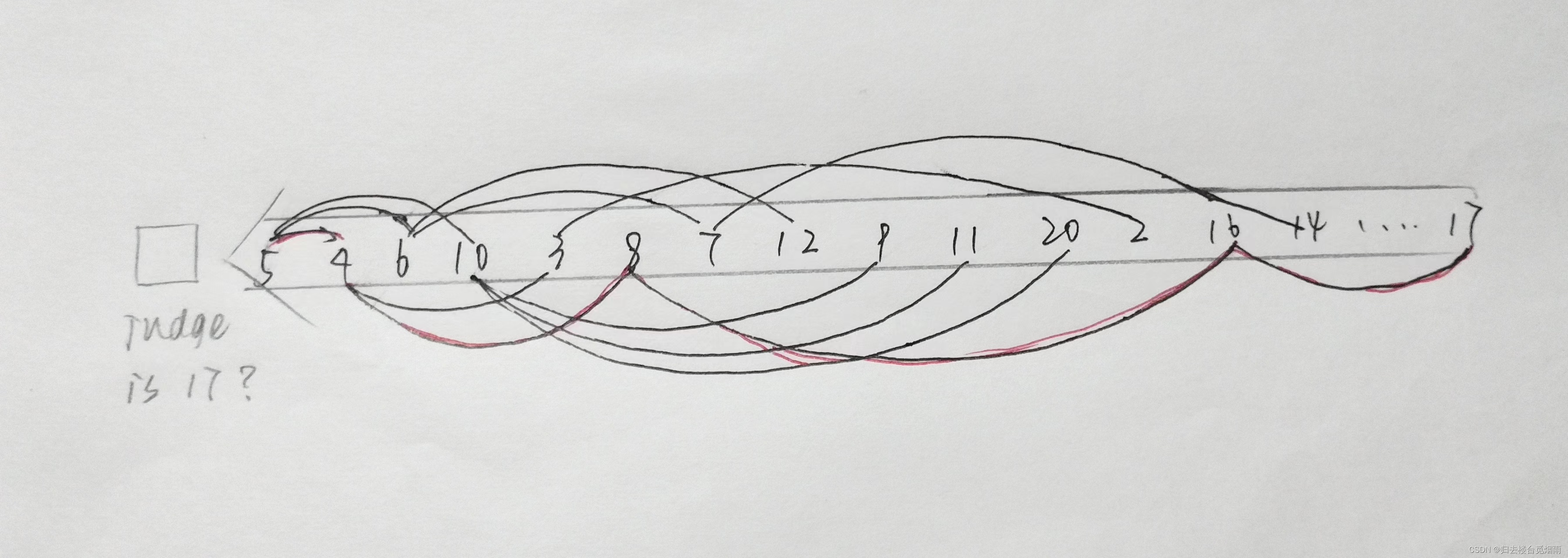
解题思路
使用队列从队尾依次传入值;判断队首值是否为所需值。
使用数组对每次将要传入的值做标记。从来没有传入过的值都标记为-1,传入且符合条件的,在上一次符合条件的标记值基础上加1。最终输出牛所在位置的标记值,即为运行了多少次。
代码部分
代码部分
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5;
int len[N];//用于标记的数组定义
int main()
{int n, k;cin >> n >> k;memset(len, -1, sizeof(len));//用于标记的数组初始化//-1:从未进入过队列; 非-1:既表示进入了队列,又表示最短路径中,已经走了第几步。queue<int>q;q.push(n);len[n] = 0;//农夫所在的第一个位置,标记为最短路径中的第0步int x;//记录队首值(为了书写方便)int y[3];//从一个位置可能延伸出的3个子位置while (!q.empty()){x = q.front();if (x == k)break;//如果检索到牛的位置,停止循环q.pop();//如果不是牛的位置,弹出队首元素y[0] = x - 1;y[1] = x + 1;y[2] = 2 * x;for(int i=0;i<3;i++)if (y[i] >= 0 && y[i] < N && len[y[i]] == -1)//判断条件:如果该位置在数组界线内且从来没有进入过队列{q.push(y[i]);//让它进入队列len[y[i]] = len[x] + 1;//又走了一步;}}cout << len[k] << endl;return 0;
}运行结果

看看len数组中各个位置的标记值
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e5;
int len[N];//用于标记的数组定义
int main()
{int n, k;cin >> n >> k;memset(len, -1, sizeof(len));//用于标记的数组初始化//-1:从未进入过队列; 非-1:既表示进入了队列,又表示最短路径中,已经走了第几步。queue<int>q;q.push(n);len[n] = 0;//农夫所在的第一个位置,标记为最短路径中的第0步int x;//记录队首值(为了书写方便)int y[3];//从一个位置可能延伸出的3个子位置while (!q.empty()){x = q.front();if (x == k)break;//如果检索到牛的位置,停止循环q.pop();//如果不是牛的位置,弹出队首元素y[0] = x - 1;y[1] = x + 1;y[2] = 2 * x;for(int i=0;i<3;i++)if (y[i] >= 0 && y[i] < N && len[y[i]] == -1)//判断条件:如果该位置在数组界线内且从来没有进入过队列{q.push(y[i]);//让它进入队列len[y[i]] = len[x] + 1;//又走了一步;}}cout << len[k] << endl;//查看:for (int i = 0; i <= k; i++)cout << i << ":" << len[i] << endl;return 0;
}运行结果:
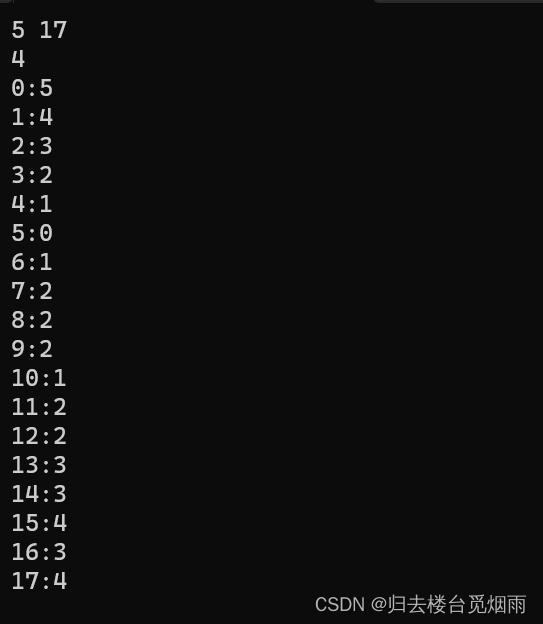
len数组中元素的实际含义:
踩到这个位置上时,这是某条路径的第len[ i ]步
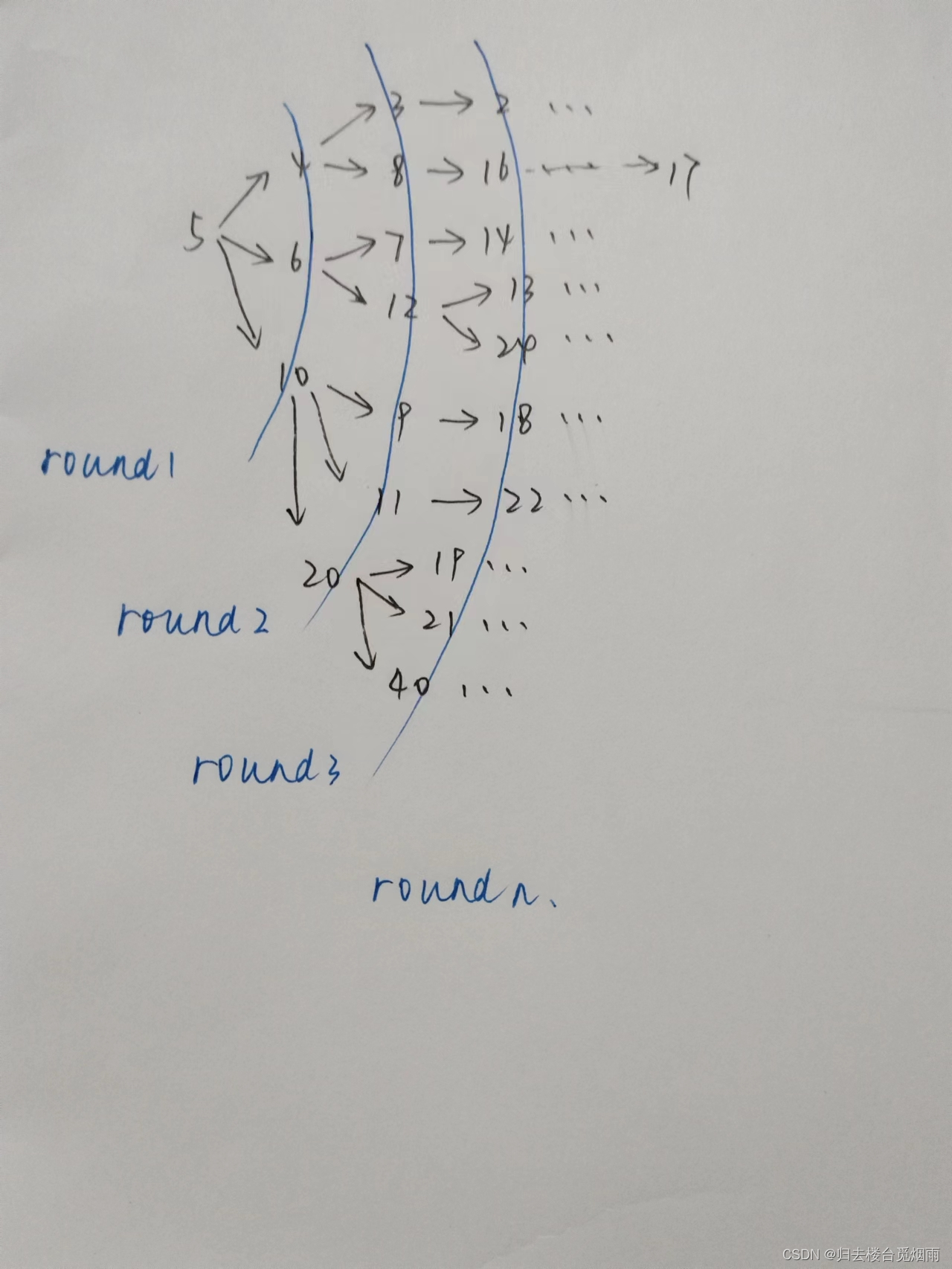
为什么这样做一定是最短路径:
关键词:广度搜索、优先输出。
将最短路径的问题转化为最先输出队列的问题。
相关文章:

1947抓住那头牛(队列 广度优先搜索)
目录 题目描述 解析 解题思路 代码部分 代码部分 运行结果 看看len数组中各个位置的标记值 为什么这样做一定是最短路径: 题目描述 农夫知道一头牛的位置,想要抓住它。农夫和牛都位于数轴上,农夫起始位于点N(0<N<100000)&…...

基于linux5.15.5的IMX 参考手册 ---21
基于linux5.15.5的IMX 参考手册 — 21 10.5.2高清多媒体接口(HDMI)和显示端口(DP)概述 10.5.2.1测试名称 •mxc_cec_test.out 10.5.2.1.1位置 /unit_tests/HDMI/ 10.5.2.1.2功能 验证HDMI CEC功能并向HDMI接收器发送断电命令。 1…...
Android Dalvik虚拟机 堆初始化流程
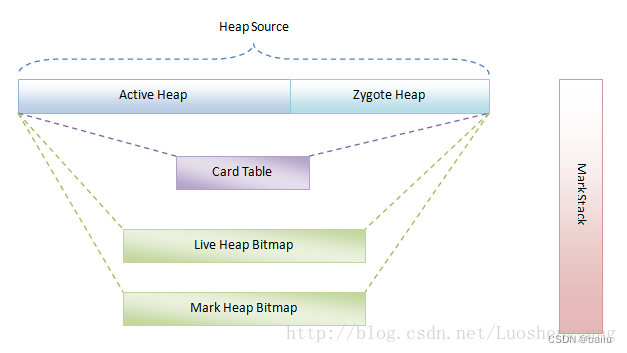
前言 上篇文章介绍了dalvik虚拟机启动流程,在dalvik虚拟机启动时调用了dvmGcStartup来启动堆。 本文介绍我们在日常开发使用Java时的堆创建流程。 Dalvik堆介绍 Dalvik虚拟机中,堆是由heap[0] Active堆和heap[1] Zygote堆两部分组成的。其中ÿ…...
——开发前必备基本常识)
0讲(补)——开发前必备基本常识
前言 专栏内容持续补充更新,目前正在进行优惠活动 目录 前言 一、函数的声明和定义 二、预编译 三、串口打印中的printf函数的使用...

JS学习笔记
1.WebAPIs简介导读Web APIs 和JS 基础关联性JS 基础阶段以及 Web APIs 阶段JS基础学习 ECMAScript 基础语法为后面作铺垫,Web APIs 是JS 的应用,大量使用JS基础语法做交互效果①JS 基础阶段我们学习的是ECMAScript 标准规定的基本语法要求同学们掌握JS 基…...

linux005之用户、组管理
linux用户管理简介: 任何使用linux系统的用户,都必须使用一个合法的账号和密码,账号和密码一般都是超级管理员创建,当然普通用户也可以创建用户,前提是必须拥有创建用户权限。 root是linux系统中默认创建的超级用户 创…...
列线图工具_Nomogram
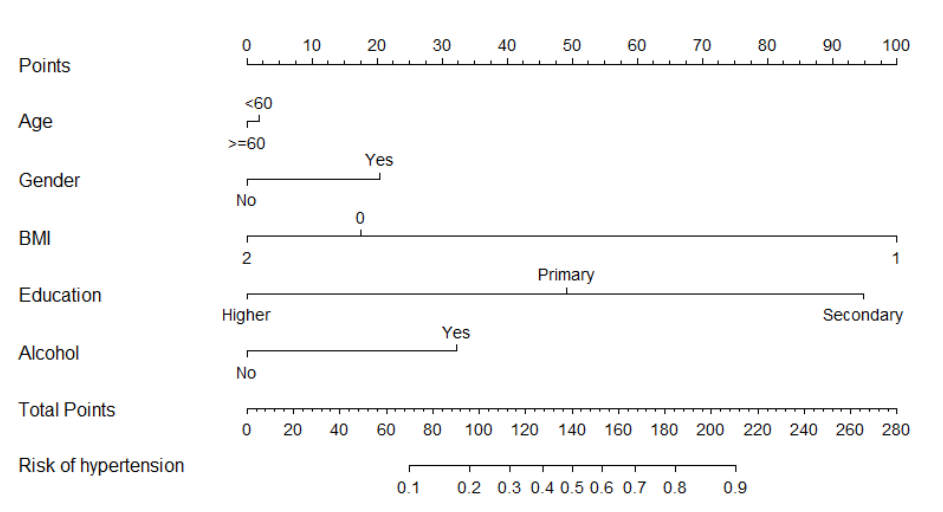
定义 列线图是一种相对传统的分析方法,用于展示自变量和因变量的线性关系,及其特征的重要程度。 现在用SHAP,和机器学习库中的 Feature importance 工具可以实现类似甚至更好效果。不过很多传统的研究领域比较认这种方法。 列线图工具建立在…...
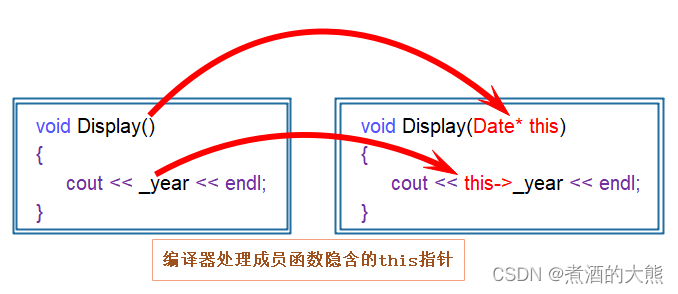
【C++】类和对象(一)
目录一、面向过程和面向对象初步认识二、类的引入三、类的定义四、类的访问限定符及封装4.1、访问限定符4.2、封装五、类的作用域六、类的实例化七、类对象的大小八、this指针8.1、this指针的引出8.2、this指针的特性8.3、C语言和C实现Stack的对比一、面向过程和面向对象初步认…...
Python获取搜索引擎结果
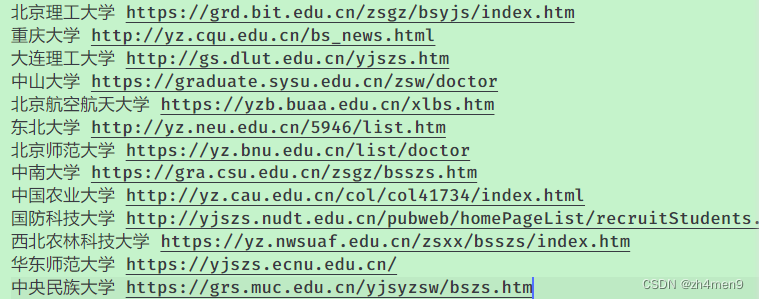
前言 想快速获取各个高校的博士招生网站,于是通过python先获取出有可能包含高校博士招生网站的URL,然后通过人为筛选得到了想要的招生网站(注意,并非直接爬取,是间接获取的)。 整理了一份网站名单&#x…...

2.4.8 PCIe——物理逻辑层——REFCLK
一、概述 pcie的参考时钟由板级输入,提供给IP内PHY层的PLL使用,由PLL产生core_clk和pipe_clk。 二、REFCLK产生方式 Serdes 所用时钟由 PHY 模块内的PLL生成,PLL的参考时钟可以由common clock(外部背板提供)、separ…...

树莓派4B arm64 搭建 docker+drone+gitea
树莓派4B arm64 搭建 dockerdronegitea 记录时间: 2023年02月10日 树莓派烧录 如何用树莓派搭建一台永久运行的个人服务器? https://mp.weixin.qq.com/s?__bizMzI5NjA0ODkwNA&mid2651847658&idx1&sn267a1257b43d4a76f2a081ed157b77f9&chksmf7b11…...

Java的JDBC编程
目录 1. 打开IDEA,新建Project 2. 引入依赖 (1)下载驱动包 (2)将驱动包导入Project 3. 编写代码 (1)创建数据源 (2)让代码和数据库服务器建立联系 (3&…...
)
CSS:块格式化上下文(BFC)
块格式化上下文是块级盒子的布局过程发生的区域,也是浮动元素与其他元素交互的区域。 块格式化上下文(BFC)的创建 满足以下条件将创建块格式化上下文: 根元素()浮动元素(float 值不为 none)绝对定位元素…...

paddle表情识别部署
表情识别模块1.环境部署1.1同样采用fastDeploy库1.2相关模型2.封装成静态库2.1参考[百度Paddle中PP-Mattingv2的部署并将之封装并调用一个C静态库](https://blog.csdn.net/weixin_43564060/article/details/128882099)2.2项目依赖添加2.3生成成功3.test3.1创建emotion_test项目…...

Python-第五天 Python函数
Python-第五天 Python函数一、函数介绍1. 什么事函数二、函数的定义1.函数的定义:2.案例三、函数的参数1.函数的传入参数2.案例升级四、函数的返回值1.什么是返回值2.返回值的语法3.None类型4.None类型的应用场景五、函数说明文档1.函数的说明文档2.在PyCharm中查看…...
【Python学习笔记】28.Python3 错误和异常
前言 作为 Python 初学者,在刚学习 Python 编程时,经常会看到一些报错信息,在前面我们没有提及,这章节我们会专门介绍。 Python3 错误和异常 Python 有两种错误很容易辨认:语法错误和异常。 Python assert…...

SQLServer 迁移到 MySQL 工具对比
我之所以会写这篇对比文章,是因为公司新产品研发真实经历过这个痛苦过程(传统基于 SQL Server开发的C/S 产品转为 MySQL云产品)。首次需要数据转换是测试环节,当时为了快速验证新研发云产品性能与结果准确性(算法类&am…...
)
分析finebi5.x仪表板组件获取数据过程(数据是数据集或者sql的)
首先仪表板的公共连接类似:http://localhost:37799/webroot/decision/link/Bo6B 当我们访问这个连接时,会来到FineLinkAction的getShareReport方法。 public String getShareReport(HttpServletRequest req, HttpServletResponse res, @FinePathVariable("linkId"…...

设计模式--适配器模式 Adapter Pattern
设计模式--适配器模式 Adapter Pattern适配器模式 Adapter Pattern1.1 基本介绍1.2 工作原理类适配器模式对象适配器模式接口适配器模式小结适配器模式 Adapter Pattern 1.1 基本介绍 (1)适配器模式将某个类的接口转换成为客户端期望的另一个接口表示&…...

PVE虚拟机篇-rest api
rest api官方介绍 Proxmox VE API rest api文档 rest api文档 rest api token 调用pve rest api ,有两种认证方式 Ticket Cookie Ticket Cookie的方式是最为推荐的,获取的方式为,通过post请求,发送用户名和密码到pve的server端获取tok…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
