2.3操作系统-进程管理:死锁、死锁的产生条件、死锁资源数计算
2.3操作系统-进程管理:死锁、死锁的产生条件、死锁资源数计算
- 死锁
- 死锁的产生条件
- 死锁资源数计算
死锁
进程管理是操作系统的核心,如果设计不当,就会出现死锁的问题。如果一个进程在等待意见不可能发生的事,进程就会死锁。而如果一个或多个进程产生死锁,就会造成系统死锁。
死锁的产生条件
死锁的产生有四大条件,互斥、保持和等待、不剥夺、环路等待。
打破其中一项即可。
假设资源是🍍🍍🍓,现在有两个进程A、B,进程A需要🍍🍍🍓,进程B需要🍍🍓,现在状态是A🍍🍍,B🍓。
B拿到了🍓,但是缺少🍍,A拿到了🍍🍍,但是没有🍓,二者都无法继续执行,此时都不释放资源,而是一直占有着。
打破死锁:破坏互斥条件
互斥表示同一时间资源只给一个线程用,线程之间资源不共享。
破坏互斥条件,资源不再是不可共享的,也就是说B的🍓可以给A用,这样A进程就可以拿到缺少的资源🍓,然后继续执行,A用完释放掉资源,再给B用。
打破死锁:破坏保持和等待
破坏保持和等待,B等待一会儿,没有资源,就释放调自己占用的资源🍓,这样A进程就可以拿到缺少的资源🍓,然后继续执行,A用完释放掉资源,再给B用。
打破死锁:不剥夺
破坏不剥夺,A去抢B的🍓,抢到后,这样A进程就可以拿到缺少的资源🍓,然后继续执行,A用完释放掉资源,再给B用。
打破死锁:环路等待
环路等待就是A等待B,B等待A,此时没有其它进程参与,AB循环等待。
进程C也参与进来了,C有🍍🍓,用完释放掉资源。
死锁资源数计算
系统有3个进程ABC,这三个进程都需要5个资源。如果系统至少有多少个资源,则不可能发生死锁。
资源数记作n,进程数记作m,每个进程需要的资源数记作W或者Wi
每个进程需要的资源数相同的情况下
n≥m×(w−1)+1n \geq m×(w-1)+1 n≥m×(w−1)+1
即最小资源数≥进程数×(单进程需要的资源数−1)+1即最小资源数 \geq 进程数×(单进程需要的资源数-1)+1 即最小资源数≥进程数×(单进程需要的资源数−1)+1
n=3×(5-1)+1=13,系统至少有13个资源,则不可能发生死锁。
每个进程需要的资源数不同的情况下,对(w-1)进行累加操作即可
系统有3个进程ABC,这三个进程依次需要3、4、5个资源。如果系统至少有多少个资源,则不可能发生死锁。
n≥(3−1)+(4−1)+(5−1)+1=10n \geq (3-1)+(4-1)+(5-1)+1=10 n≥(3−1)+(4−1)+(5−1)+1=10
相关文章:

2.3操作系统-进程管理:死锁、死锁的产生条件、死锁资源数计算
2.3操作系统-进程管理:死锁、死锁的产生条件、死锁资源数计算死锁死锁的产生条件死锁资源数计算死锁 进程管理是操作系统的核心,如果设计不当,就会出现死锁的问题。如果一个进程在等待意见不可能发生的事,进程就会死锁。而如果一…...

人物百科怎么建?个人百度百科创建的注意事项
百科词条根据百科类型可分为人物词条、品牌词条以及企业词条等等,对于不同类型的词条,在创建时有着不同的规则要求。 相对于品牌词条和企业词条,人物词条是相对有难度的一类,因为品牌有注册商标,企业有营业执照,都是比较容易佐证的…...
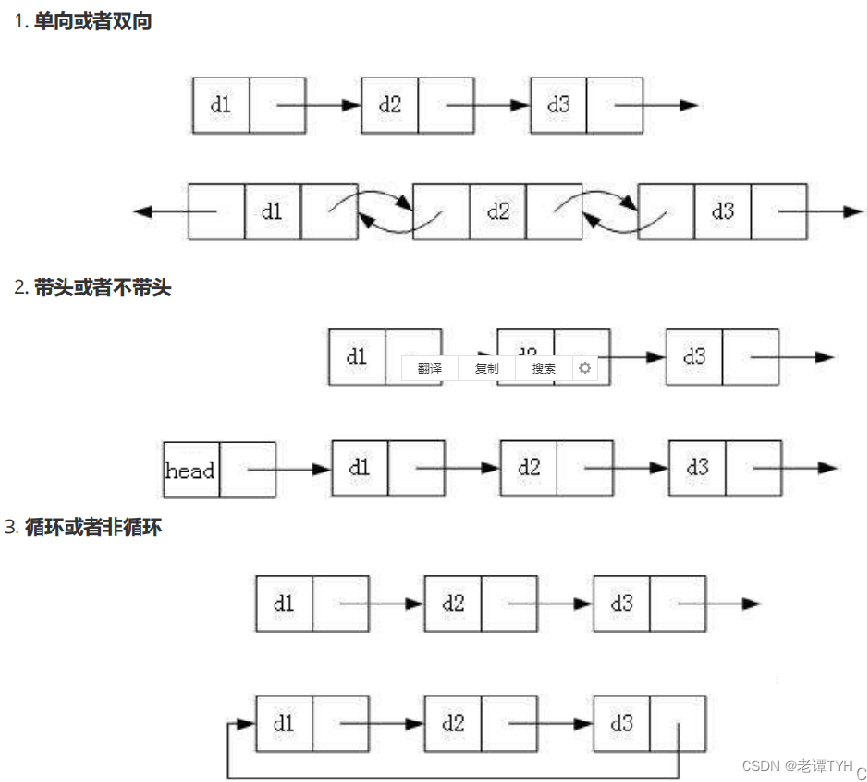
ArrayList与LinkedList的区别 以及 链表理解
list接口中ArrayList、LinkedList都不是线程安全,Vector是线程安全 1、数据结构不同 ArrayList是Array(动态数组)的数据结构,LinkedList是Link(链表)双向链表的数据结构。 2、空间灵活性 ArrayList最好指定初始容量 LinkedList是比ArrayList灵活的&a…...
电脑蓝屏怎么办?这5个技巧你必须学会
案例:电脑蓝屏是什么原因?怎么样可以解决? “救命!!!电脑是怎么了?开机直接蓝屏,是哪里坏了吗?前几天电脑还是好的,今早一打开就是蓝屏,可能是之…...
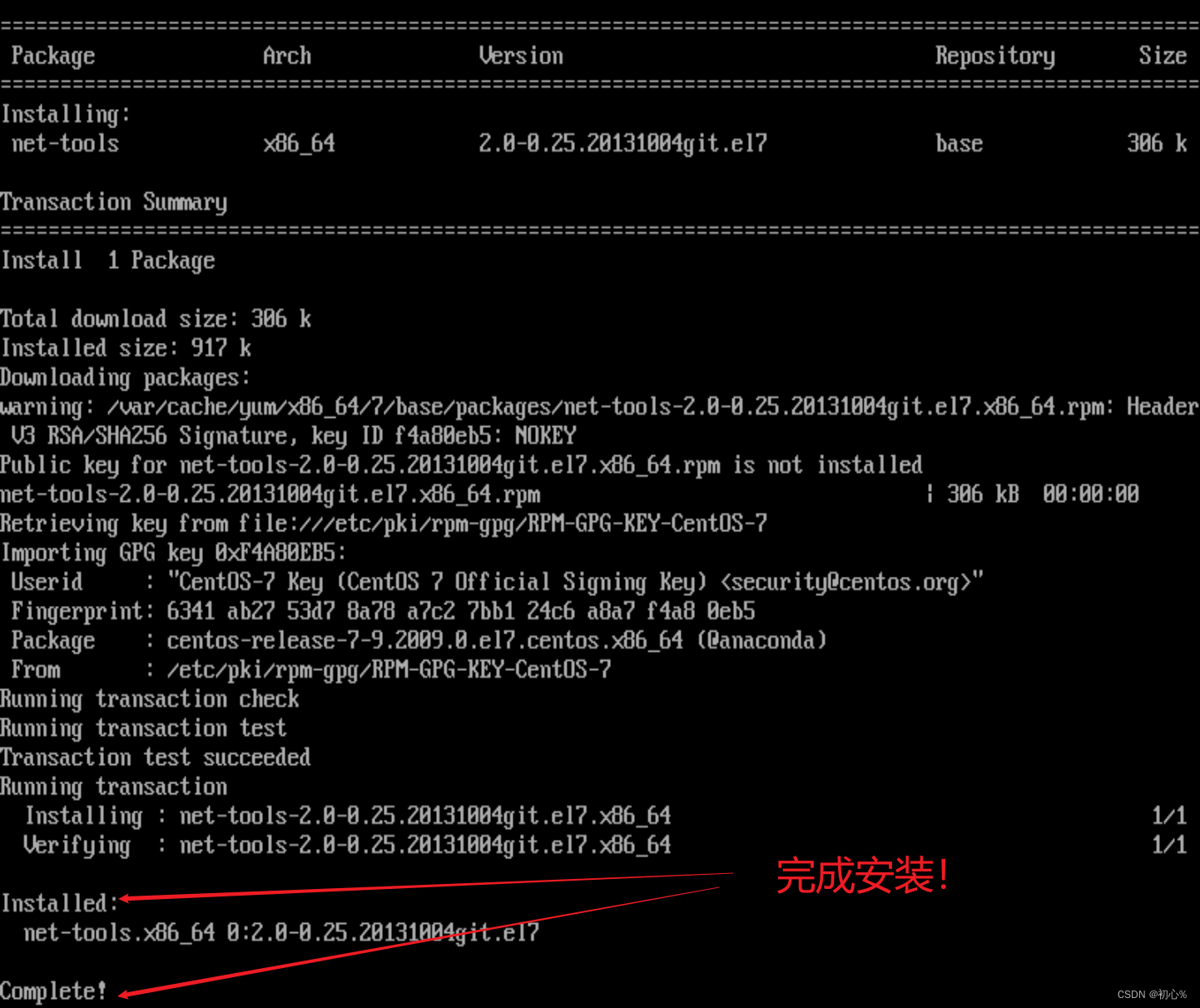
大数据 | (三)centos7图形界面无法执行yum命令
大家好,今天是三八女神节了! 你知道吗?世界上第一位电脑程序设计师是名女性,Ada Lovelace (1815-1852)。 她是一位英国数学家兼作家,第一位主张计算机不只可以用来算数的人,也发表了第一段分析机用的演算…...

历史上被发现的第一个真正的Bug - Grace Hopper
写在前面:博主是一只经过实战开发历练后投身培训事业的“小山猪”,昵称取自动画片《狮子王》中的“彭彭”,总是以乐观、积极的心态对待周边的事物。本人的技术路线从Java全栈工程师一路奔向大数据开发、数据挖掘领域,如今终有小成…...

KiCad 编译
KiCad 编译 因为最新项目需要,所以看了一下KiCad的编译,这里介绍的是64位电脑的编译,32位小伙伴请绕道官网看教程呦。 您可以在KiCad内查看基本的编译教程。 我这里也是参考的官网编译教程进行的编译,接下来让我们一起看看吧。…...

HTML 简介
文章目录HTML 简介实例解析什么是HTML?HTML 标签HTML 元素Web 浏览器HTML 网页结构HTML版本<!DOCTYPE> 声明通用声明HTML5HTML 4.01XHTML 1.0中文编码HTML 简介 HTML 实例 <!DOCTYPE html> <html><head><meta charset"utf-8"><ti…...
)
2023浙江省赛“信息安全管理与评估“--数字取证调查--网络数据包分析解析(高职组)
2022全国职业技能大赛“信息安全管理与评估”(高职组)任务书 2022全国职业技能大赛“信息安全管理与评估”任务书第一阶段竞赛项目试题第二阶段竞赛项目试题任务 2: 网络数据包分析第三阶段竞赛项目试题2022全国职业技能大赛“信息安全管理与评估”任务书 第一阶段竞赛项目…...
【Redis应用】查询缓存相关问题解决(二)
🚗Redis应用学习第二站~ 🚩起始站:【Redis应用】基于Redis实现共享session登录(一) 🚩本文已收录至专栏:Redis技术学习 👍希望您能有所收获,底部附有完整思维导图 一.概述 本篇我们会一起来学习…...
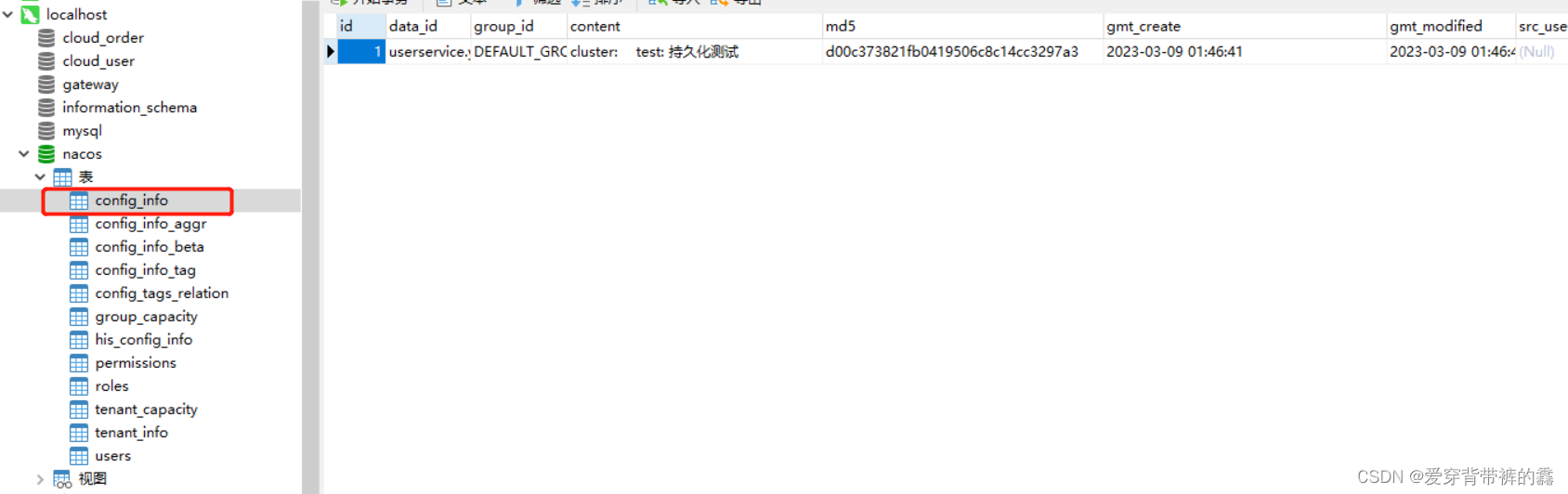
【SpringCloud】SpringCloud教程之Nacos实战(三集群配置)
目录前言一.Nacos集群逻辑图二.Nacos集群搭建1.搭建数据库,初始化数据库表结构2.下载Nacos3.配置Nacos3.启动Nacos4.配置启动nginx5.测试是否成功6.设置服务的nacos地址7.新增一个配置,查看数据看是否进行持久化了前言 在我前面两篇讲的都是单个nacos&a…...

什么是激励能力?HR人才测评
什么是激励能力?激励能力主要是针对管理型岗位而言的,尤其是团队型管理,既要督导团队成员,更需要掌握激励下属的方法和技巧。在HR人才测评系统中,对于管理型岗位的人才测评指标,通常也会包含激励能力&#…...

【刷题笔记】之滑动窗口(长度最小的子数组、水果成篮、最小的覆盖子串)
滑动窗口模板//滑动窗口模板:注意使用滑动窗口方法,使用一个 for(while) 循环中的变量是用来控制终止位置的//最小滑窗:给定数组 nums,定义滑动窗口的左右边界 i、j,求满足某个条件的滑窗的最小长度 for(j 0; j < …...

【JavaScript速成之路】JavaScript函数
📃个人主页:「小杨」的csdn博客 🔥系列专栏:【JavaScript速成之路】 🐳希望大家多多支持🥰一起进步呀! 文章目录前言1,函数基础1.1,函数概念1.2,函数使用1.3&…...

萤火虫算法优化SVM变压器故障分类预测,fa-svm分类预测,libsvm参数优化
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 SVM应用实例,基于fa-svm分类预测 代码 结果分析 展望 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是…...
JavaScript DOM API的使用
文章目录一. 什么是DOM二. 最常用的DOM API1. 选中页面元素2. 操作元素的属性2.1 事件概念2.2 获取/修改元素内容计数器2.4 获取/修改元素属性点击图片切换2.5 获取/修改表单元素属性表单计数器全选/取消全选按钮2.6 获取修改样式属性点击文字放大实现夜间/日间模式的切换3. 操…...
Vue组件库出现$listeners is readonly等错误的原因及预防方法
本文主要是面向写组件库的人士,而不是组件库的使用人士。 出现原因 根本原因是因为组件库的package.json中 dependencies包含了vue包,然后导致最后打包出来的组件库也包含vue包 然后和引用这个组件库的项目中的vue发生冲突。 举个例子,pro…...

lsusb
用法: lsusb -hUsage: lsusb [options]... List USB devices -v, --verbose Increase verbosity (show descriptors) -s [[bus]:][devnum] Show only devices with specified device and/or bus numbers (in decimal) -d vendor:[product] …...

Allegro如何在PCB中添加层面操作指导
Allegro如何在PCB中添加层面操作指导 在用Allegro做PCB设计的时候,根据需要,会在PCB中额外添加一些额外的层面,如下图 如何添加,具体操作如下 点击Setup点击Subclasses...

淘宝widget链路方案总结
目前widget生态已经做了大量的基建工作,同时在widget生态的演进过程中我们发现如何匹配用户的偏好一直以来是一个挑战工作,本文介绍了widget的整体链路。业务背景▐ widget介绍2020年底iOS推出了新版widget之后引起了一些声浪,但仍然很多苹果用户并不了…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
