【算法】六大排序 插入排序 希尔排序 选择排序 堆排序 冒泡排序 快速排序
本章的所有代码可以访问这里
排序 一
- 一、排序的概念及其运用
- 1.1排序的概念
- 1.2 常见的排序算法
- 二、常见排序算法的实现
- 1、直接插入排序
- 2、希尔排序
- 3、选择排序
- 4、堆排序
- 5、冒泡排序
- 6、快速排序
- 6.1霍尔法
- 6.2挖坑法
- 6.3前后指针法
- 7、快速排序非递归
一、排序的概念及其运用
1.1排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2 常见的排序算法

二、常见排序算法的实现
1、直接插入排序
- 基本思想
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
<实际中我们玩扑克牌时,就用了插入排序的思想>

- 步骤
假设我们进行升序排序

-
我们首先认为我们第一个数据是有序的。
-
取一个数据data,将已排序的元素序列从后往前遍历
-
如果遍历过程中发现已排序的元素序列中的某个数据largeData大于data那我们就将数据largeData向后移动一个单位,然后继续向前遍历。如果已排序的元素序列中的某个数据smallerData小于data,那我们就将数据data放到smallerData的后面,然后就不需要向前遍历了,因为已排序的元素序列经过上面的2-3步骤后新来的数据data也被放到了正确的位置。

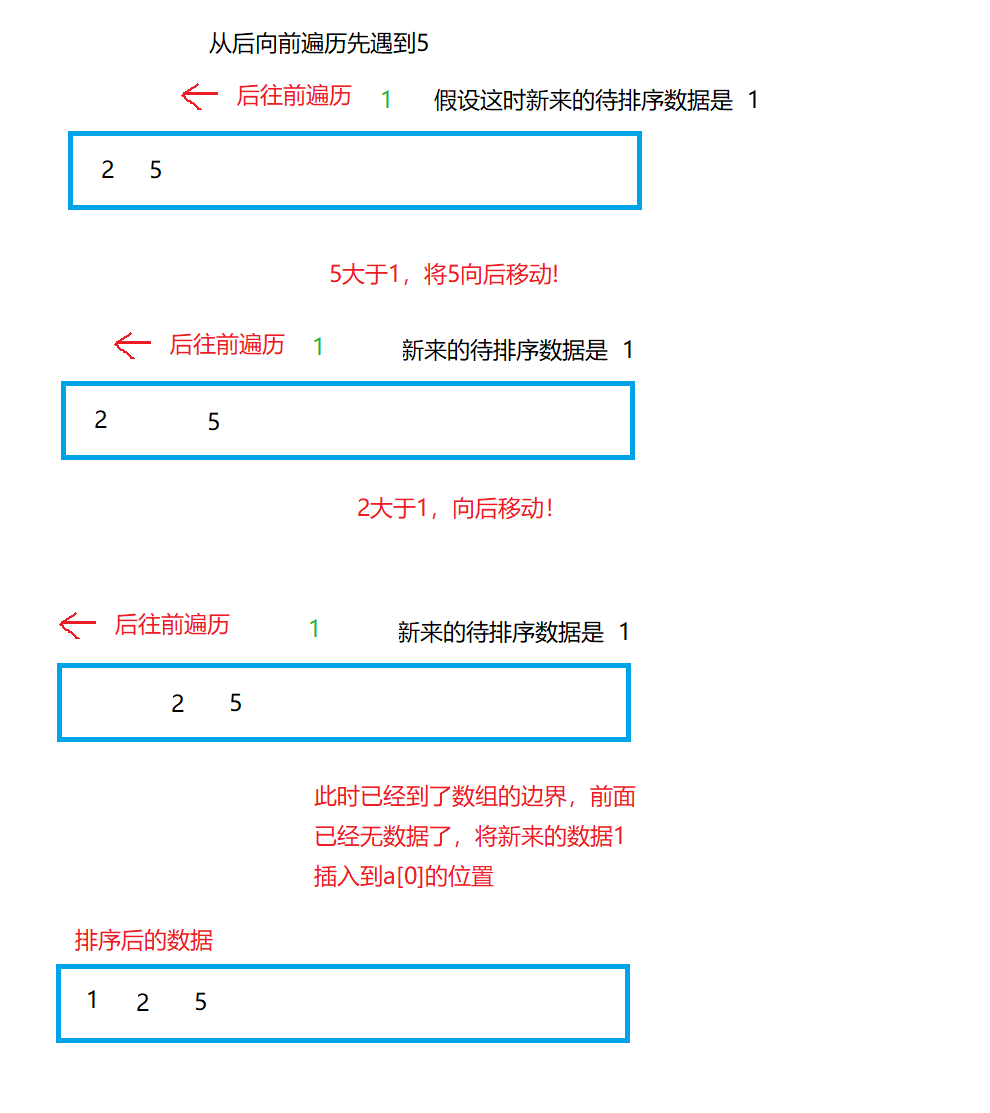
-
所以我们对许多数据进行排序就被转化为上面2-3步骤的循环了。
动图演示

- 代码实现
//直接插入排序
void InsertSort(int* a,int n)
{//排序 for (int i = 0; i + 1 < n; i++){//end是有序数列的最后一个位置的下标int end = i;int tmp = a[end + 1];//end >= 0 防止在--end时数组越界while (end >= 0 && tmp < a[end]){a[end +1] = a[end];--end;}a[end+1] = tmp;}
}- 直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高(因为数据越接近于有序,向后挪动的次数就越小)
- 最坏情况下为O(n2)O(n^2)O(n2),此时待排序列为逆序,或者说接近逆序
最好情况下为O(n)O(n)O(n),此时待排序列为升序,或者说接近升序 - 空间复杂度:O(1)O(1)O(1),它是一种稳定的排序算法
- 稳定性:稳定
2、希尔排序
希尔排序法的步骤是:
先选定一个小于N(N为数组的个数)的整数gap,把所有数据分成gap个组,所有距离为gap的数据分在同一组内,并对每一组的元素进行直接插入排序。然后取新的gap(新的gap要小于上一个gap),重复上述分组和排序的工作。当到达gap=1时,所有数据在同一组内排好顺序。
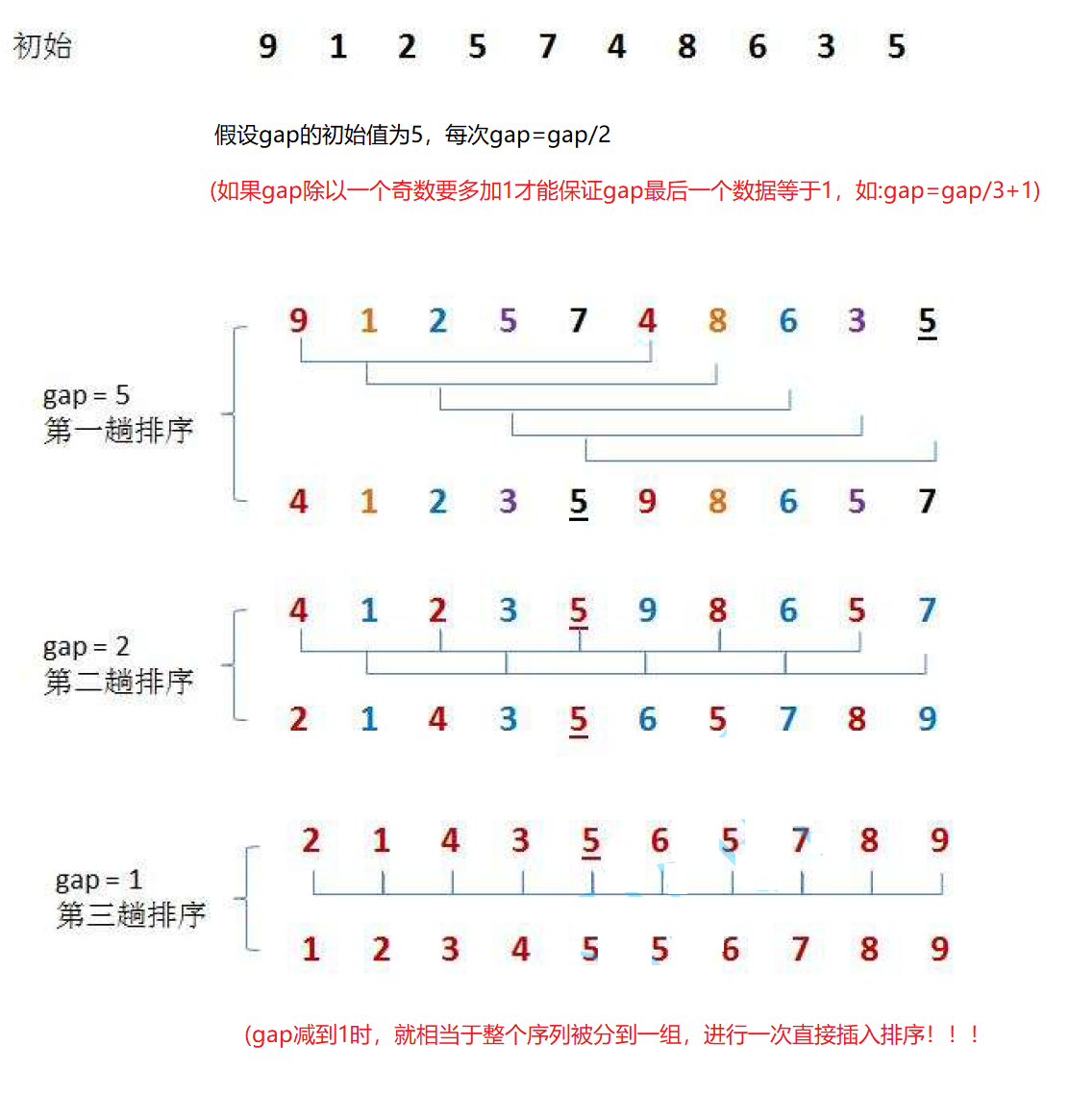
希尔排序法的思想是:
希尔排序先将待排序列通过gap分组进行预排序(gap>1时都是预排序),使待排序列接近有序,然后再对该序列进行一次插入排序(gap=1时其实就是插入排序),此时插入排序的时间复杂度接近于O(N)
代码实现
//希尔排序 正常一组一组排序
void ShellSort(int* a,int n)
{//定义第一次gap的值 int gap = n;//多次预排序,gap=1时是直接排序while (gap > 1){//减小gap的值直到1gap = gap / 3 + 1;//多趟排序for (int j = 0; j < gap; j++){//单趟排序 i是当前有序序列最后一个位置的下标for (int i = j; i + gap < n; i += gap){int end = i;//记录一下待插入的数据int tmp = a[end + gap];//end >= 0 防止在end -=gap 时数组越界while (end >= 0 && tmp < a[end]){a[end + gap] = a[end];end -= gap;}a[end + gap] = tmp;}}}
}
- 希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些书中给出的希尔排序的时间都不固定。
- 时间复杂度平均:O(N1.3)O(N^{1.3})O(N1.3)
- 空间复杂度:O(1)O(1)O(1)
- 稳定性:不稳定
3、选择排序
基本思想:
每一次从待排序的数据元素中选出最小和最大的一个元素,存放在序列的起始位置和末尾位置,然后起始位置向后移动一个单位,末尾位置向前移动一个单位,直到全部待排序的数据元素排完 。
步骤:
遍历一遍整个数组,选出最大值和最小值,第一次将最小值放到a[0]最大值a[n-1],第二次将最小值放到a[1]最大值a[n-2],直到下标m>=n−m−1m >= n-m-1m>=n−m−1结束程序。
动态演示
(下图演示的是一次只选一个最小值的算法,我们一次选出最大和最小,比图中的更高效一些)

代码实现
//选择排序
void SelectSort(int* a, int n)
{//多趟排序int begin = 0;int end = n - 1;while (begin < end){//先假设 a[0] 位置既是最小值又是最大值//mini是最小值的下标,maxi是最大位置的下标int mini = begin, maxi = begin;//单趟遍历,选出最大值于最小值for (int i = begin; i <=end; ++i){if (a[i] > a[maxi]){maxi = i;}else if (a[i] < a[mini]){mini = i;}}Swap(&a[begin], &a[mini]);if (begin == maxi){maxi = mini;}Swap(&a[end], &a[maxi]);++begin;--end;}
}
直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
4、堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
堆排序详情请看这里
堆排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
5、冒泡排序
基本思想:
两两进行比较,左边大于右边就进行交换,走完一趟就排序好一个数。

代码实现
//冒泡排序
int BubbleSort(int*a,int n)
{for (int j = 0; j < n; j++){//end是排序数组的最后一个需要排序元素的下标int end = n - 1 - j;//定义一个交换标志int exchange = 0;for (int i = 0; i < end; i++){if (a[i] > a[i + 1]){Swap(&a[i], &a[i + 1]);exchange = 1;}}// 一趟冒泡过程中,没有发生交换,说明已经有序了,不需要再处理if (exchange == 0){break;}}
}
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
6、快速排序
基本思路:
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
6.1霍尔法
步骤:
- 首先选出一个key值作为基准值,通常选择待排序列的最左边的值作为key值。
- 定义两个下标,left与right,其中left指向待排序列的最左边值的下标,right指向待排序列最右边的下标。
- 如果我们选择了最左边作为key值,我们就要让right位置判断a[right] < key如果成立,那就让right暂时停下来;如果不成立,就让right- -,直到找到一个位置a[right] < key ,找到后,right就暂时停下来。(需要注意的是:若选择最左边的数据作为key,则需要right先走;若选择最右边的数据作为key,则需要begin先走)。
- right停下来之后,我们就要让左边的left的位置判断 a[left] > key 如果成立,就将a[left]与a[right]进行交换 ,如果不成立我们就将left++,直到找到一个位置a[left] > key ,找到后就与a[right]进行交换。
- 然后重复3-4,直到 left=right 时,我们将key与a[ left ] ( 此时a[left]=a[right] )进行交换,此时key就到了正确的位置,key将数组分成了两部分,此时key的左边都比key小,key的右边都比key大,一次单趟排序完成,一次单趟排序搞定了一个数据。
- 我们再对上一次的key的左右边的数组再进行上面的步骤,直到每个被分割的小区间都有序了,整个数组的排序就完成了。(最后当左右序列只有一个数据,或是左右序列不存在时,其实小区间就已经有序了)
动态演示

代码实现
//快速排序 hoare法 void QuickSort(int* a, int begin, int end)
{//当区间只有一个值时,或区间不存在时退出递归if (begin >= end){return;}//left是闭区间最最左边的下标,right是最右边位置的下标int left = begin, right = end;//选择最左边作为key值int keyi = left;//一趟排序while (left < right){//右边先走,找到a[right]<key的位置while (left < right && a[right] >= a[keyi]){--right;}//左边后走,找到a[left]>key的位置while (left < right && a[left] <= a[keyi]){++left;}//交换左右两边的值,如果left == right了,也没有必要交换了。if (left != right){Swap(&a[left], &a[right]);}}//交换左右两边的值,如果keyi == left了,也没有必要交换了。if (keyi != left){Swap(&a[keyi], &a[left]);}keyi = left;//此时区间被分割为[begin,keyi-1] keyi [keyi+1,end]//注意传递的是begin,不是0,中间递归时不一定是从0开始的区间,0是一个常量,begin是一个变量。QuickSort(a, begin, keyi-1);QuickSort(a, keyi+1, end);
}
6.2挖坑法
步骤:
- 先将待排序列的最左边的值定为key,用一个临时变量保存key的值同时该位置的下标定为第一个坑位hole。
- 右边right寻找比key小的值,找到后放进坑位中,同时将坑位的位置更新为right。
- 左边left寻找比key大的值,找到后放进坑位中,同时将坑位的位置更新为left。
- 重复2-3步骤直到left==right,然后将key放到相遇位置,a[left]=key(或a[right]=key)
- 此时单趟排序就排序好了,key的左边的值比key小,key右边的值比key大,key到了正确的位置,区间被分为两份,一次单趟排序好一个数。
- 再对分割后的区间,进行多次上述的单趟排序,整个数组就有序了!

//快速排序 挖坑法
void QuickSort(int* a, int begin, int end)
{//当区间只有一个值时,或区间不存在时退出递归if (begin >= end){return;}int left = begin, right = end;int keyi = left;//刚开始时keyi的位置作为坑位int hole = keyi;int key = a[keyi];while (left < right){while (left < right && a[right] >= key){--right;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;keyi = hole;//此时区间被分割为[begin,keyi-1] keyi [keyi+1,end]//注意传递的是begin,不是0,中间递归时不一定是从0开始的区间,0是一个常量,begin是一个变量。QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}
6.3前后指针法
步骤:
- 初始时,我们选定待排序的数据最左边作为key,定义prev也在待排序的数据最左边,定义cur在待排序的数据最左边+1。
- cur向前找比key小的值,找到后停下来,然后++prev,交换prev位置和cur位置的值,当prev与cur拉开差距时,prev与cur之间夹的值都是大于等于key的值。
- 最后cur刚好越界时,数组遍历完毕,交换a[prev]与key,此时key到了正确的位置,区间被分为两份,一次单趟排序好一个数。
- 再对分割后的区间,进行多次上述的单趟排序,整个数组就有序了!

//快速排序 前后指针法
void QuickSort(int* a, int begin, int end)
{//当区间只有一个值时,或区间不存在时退出递归if (begin >= end){return;}int prev = begin , cur = begin + 1;int keyi = begin;while (prev <= cur && cur <= end){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;//此时区间被分割为[begin,keyi-1] keyi [keyi+1,end]//注意传递的是begin,不是0,中间递归时不一定是从0开始的区间,0是一个常量,begin是一个变量。QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}
快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
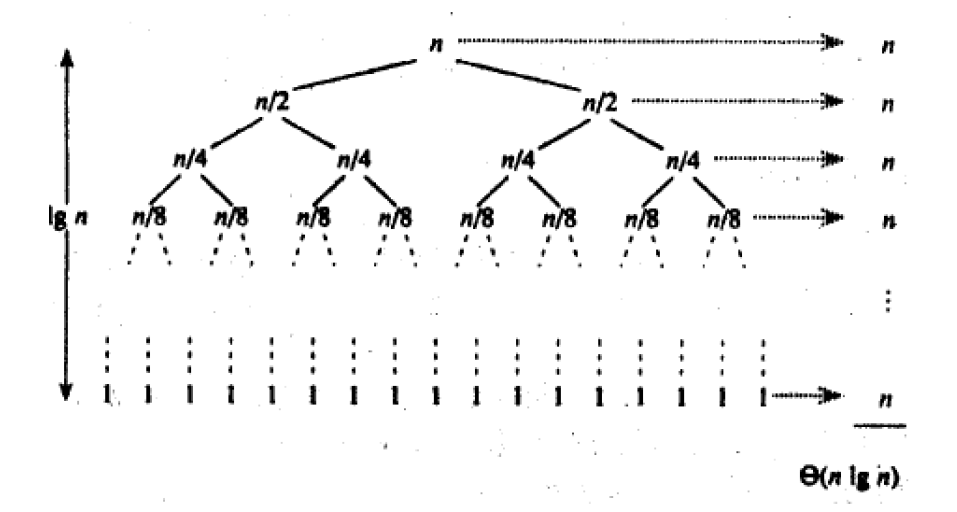
- 空间复杂度:O(logN)
- 稳定性:不稳定
7、快速排序非递归
快速排序的非递归实现要依赖栈,我们对快速排序进行递归时传递的关键数据是区间的下标,只有拿到了区间的下标我们才能进行正确的排序。
因此我们应该用利用栈的特性将区间的下标存放起来。
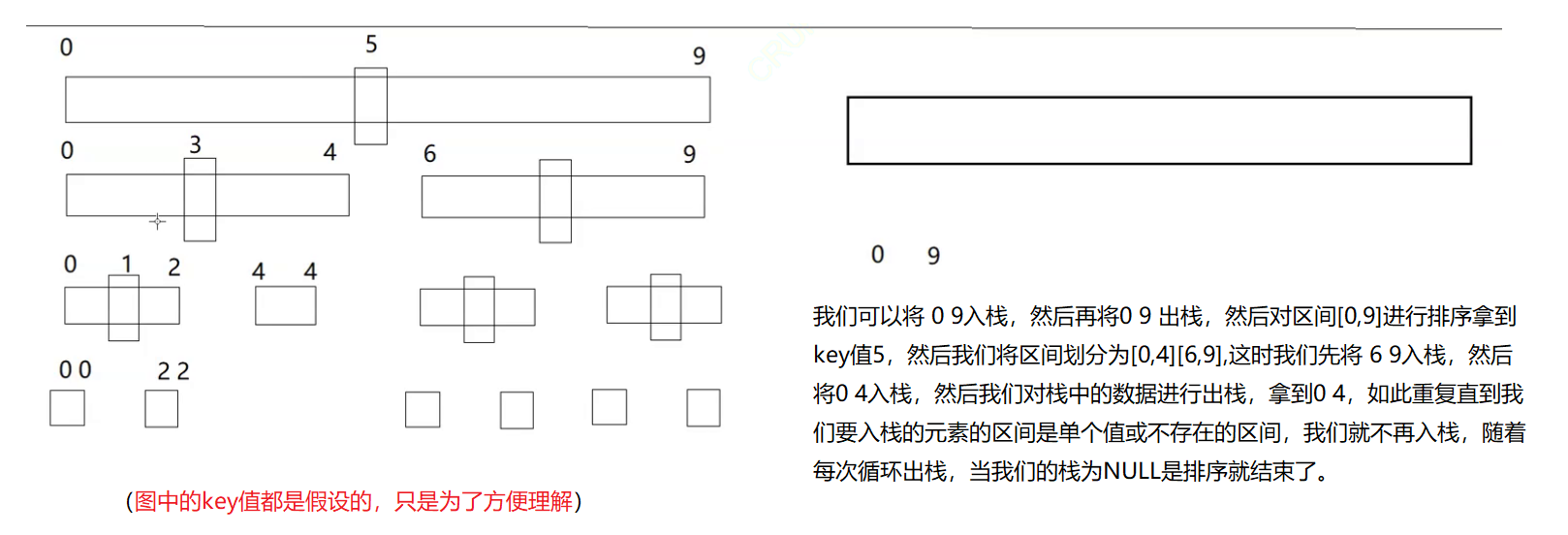
代码实现:
//单趟排序
int Partion3(int* a ,int begin ,int end)
{int prev = begin , cur = begin + 1;int keyi = begin;while (prev <= cur && cur <= end){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;return keyi;
}
//快速排序的非递归实现
void QuickSortNonR(int* a ,int begin ,int end)
{Stack st;StackInit(&st);StackPush(&st, begin);StackPush(&st, end);while (!StackEmpty(&st)){int right = StackTop(&st);StackPop(&st);int left = StackTop(&st);StackPop(&st);//一趟排序int keyi = Partion3(a, left, right);//此时区间被划分为[left,keyi-1]keyi[keyi+1,right]if (keyi + 1 < right){StackPush(&st, keyi + 1);StackPush(&st, right);}if (left < keyi - 1){StackPush(&st, left);StackPush(&st, keyi - 1);}}StackDestroy(&st);
}相关文章:

【算法】六大排序 插入排序 希尔排序 选择排序 堆排序 冒泡排序 快速排序
本章的所有代码可以访问这里 排序 一 一、排序的概念及其运用1.1排序的概念1.2 常见的排序算法二、常见排序算法的实现1、直接插入排序2、希尔排序3、选择排序4、堆排序5、冒泡排序6、快速排序6.1霍尔法6.2挖坑法6.3前后指针法7、快速排序非递归一、排序的概念及其运用 1.1排序…...

类和对象万字详解
目录 一、面向对象与面向过程的区别 面向过程: 面向对象: 二、类的引入 class与struct爱恨情仇 class的语法 类的定义: 类的限定访问符 类的实例化 类对象模型 this指针的应用 三、封装 四、类的六个默认成员函数 构造函数 再谈…...
如何使用码匠连接 CouchDB
目录 在码匠中集成 CouchDB 在码匠中使用 CouchDB 关于码匠 CouchDB 是一种开源的 NoSQL 数据库服务,它使用基于文档的数据模型来存储数据。CouchDB 的数据源提供了高度可扩展性、高可用性和分布式性质。它支持跨多个节点的数据同步和复制,可以在多个…...
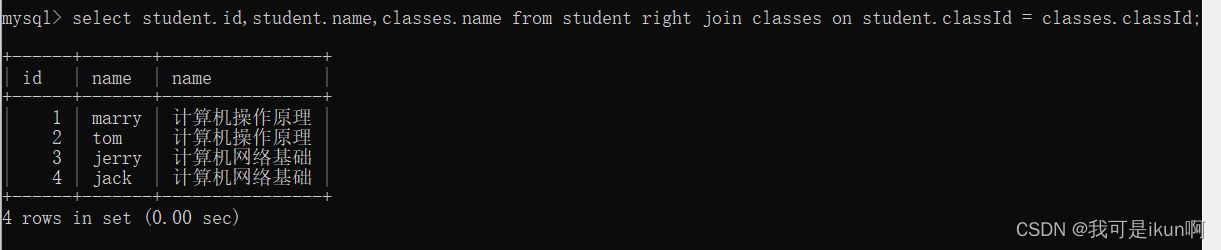
MySQL对表操作
结束了上一章内容,我们对数据库的操作有一定的了解,本章内容就是针对表中的数据进行操作的。 针对表中数据的操作绝大部分都是增删改查(CRUD),CRUD也就是四个单词的缩写: 增加(Create)、查询(Retrieve)、…...
springboot3整合mybatis遇到的坑
本人不经常写java,本文仅作问题记录,如有问题请把不吝赐教。 坑1、Property sqlSessionFactory or sqlSessionTemplate are required Caused by: java.lang.IllegalArgumentException: Property sqlSessionFactory or sqlSessionTemplate are required…...
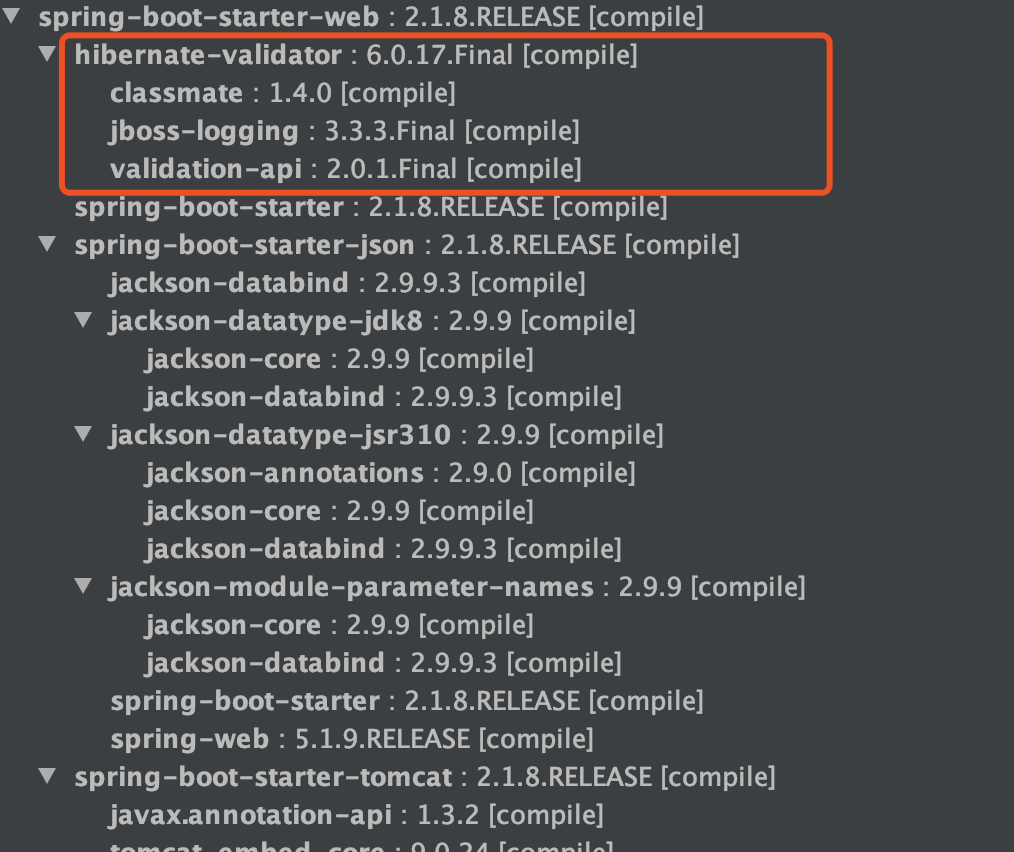
SpringBoot+Spring常用注解总结
1. SpringBootApplication 这里先单独拎出SpringBootApplication 注解说一下,虽然我们一般不会主动去使用它。 SpringBootApplication public class SpringSecurityJwtGuideApplication {public static void main(java.lang.String[] args) {SpringApplication.ru…...
优化UnRaid容器的WebUI端口设置实现应用快捷访问的方法
文章目录前言详细流程前言 自从入了UnRaid的坑,发现Docker真是个好东西,各种各样的应用工具层出不穷,可以大大提高生产效率。然而在安装Docker应用后,对于如何方便的访问该应用,各个应用服务提供者给出的解决方案不是…...

Android Framework-管理Activity和组件运行状态的系统进程—— ActivityManagerService(AMS)
ActivityManagerService(AMS)是Android提供的一个用于管理Activity(和其他组件)运行状态的系统进程 AMS功能概述 和WMS一样,AMS也是寄存于systemServer中的。它会在系统启动时,创建一个线程来循环处理客户…...
【C语言】结构体和共用体
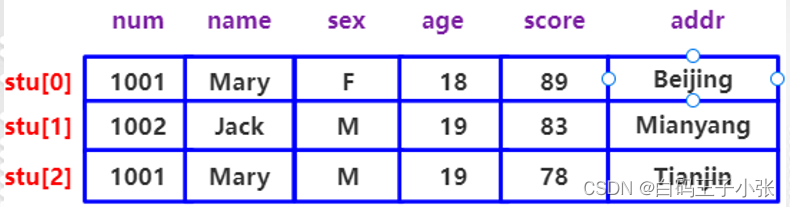
目录一、结构体(一)结构体声明(二)结构体变量定义(三)结构体变量的初始化(四)结构体的引用(五)结构体数组二、共用体(一)共用体定义&a…...

微搭低代码从入门到实战
低代码从21年起开始成为热点,至今已经发展了两年多的时间。微搭作为腾讯云旗下的低码产品也历经多轮优化。 不同人选择低代码有不同的理由,有的是初创企业希望低代码来提升运营效率的。有的是传统企业,希望借助低代码来改造现有系统提供移动…...
AM5728(AM5708)开发实战之安装Debian 10桌面操作系统
一 环境搭建 准备一个SD卡启动卡,能够正常引导板卡启动,后续会把Debian 10镜像安装到SD卡ext4分区 准备两个U盘,一个格式化成fat32文件系统,另一个格式化成ext4文件系统 下载Debian 10镜像,镜像名字为debian-10.4.0-a…...
ip-guardip-guard如何通过准入网关对指定的服务器进行通讯加密保护?
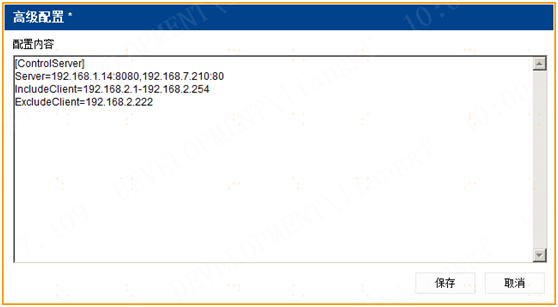
1、准入网关在高级配置设置受保护服务器; WEB管理界面【系统工具】,点击【配置管理】,点击参数设置,进入高级配置界面,输入配置内容即可。 [ControlServer]...
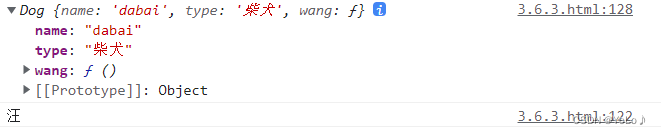
JavaScript基础语法
目录 1.初识JavaScript 1.1背景知识 1.2JS的三种书写方式 行内式 内嵌式 外部式 2.语法简介 2.1变量的使用 变量创建方法 动态类型 2.2基本数据类型 2.3数组 js数组创建方式 遍历方式 添加元素:尾插 编辑删除元素:splice 2.4函数 格式 函数表达式 作用域…...
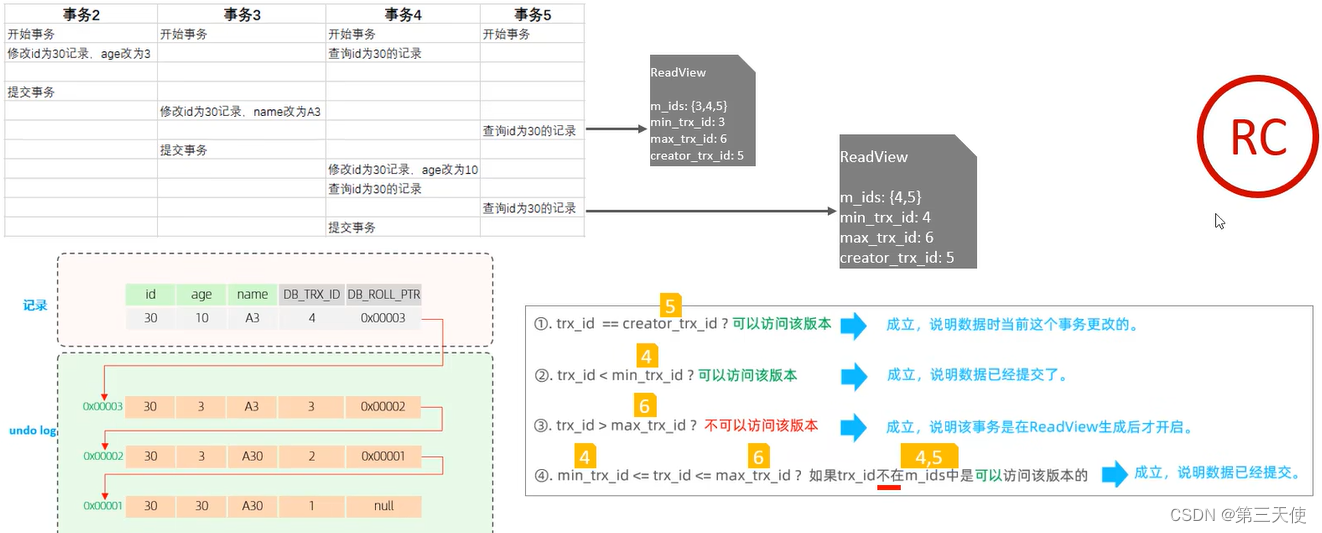
《SQL基础》17. InnoDB引擎
InnoDB引擎InnoDB引擎逻辑存储结构架构内存结构磁盘结构后台线程事务原理事务基础redo logundo logMVCC基本概念隐式字段undo log版本链readView原理分析InnoDB引擎 逻辑存储结构 InnoDB的逻辑存储结构如下图所示: 表空间 表空间是InnoDB存储引擎逻辑结构的最高层…...
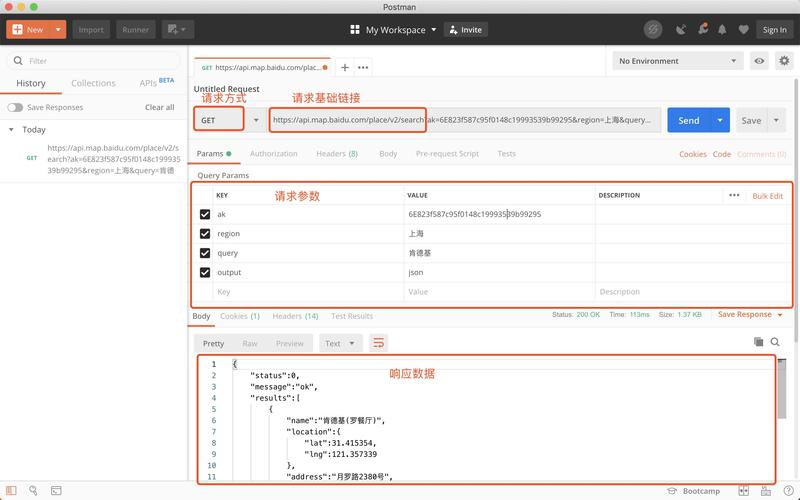
api接口详解大全
api接口详解大全?优秀的设计是产品变得卓越的原因设计API意味着提供有效的接口,可以帮助API使用者更好地了解、使用和集成,同时帮助人们有效地维护它每个产品都需要使用手册,API也不例外在API领域,可以将设计视为服务器和客户端之…...

为什么要用VR全景?5个答案告诉你
看中了刚上市的一款新车,再也不用等车展、去4s店才能仔细观赏,点开手机就能“置身”车内近距离观看每一处细节,点击关灯开灯、关门关门,除了摸不到,和在现场几乎没有区别; 准备买房的时候,没人愿…...

常用的深度学习优化方式
全连接层 PyTorch中的全连接层(Fully Connected Layer)也被称为线性层(Linear Layer),是神经网络中最常用的一种层。全连接层将输入数据的每个元素与该层中的每个神经元相连接,输出结果是输入数据与该层的…...

全面吃透Java Stream流操作,让代码更加的优雅
文章目录1 认识Stream流1.1 什么是流1.2 流与集合1.2.1 流只能遍历一次1.2.2 外部迭代和内部迭代1.3 流操作1.3.1 中间操作1.3.2 终端操作1.3.3 使用流2 学会使用Stream流2.1 筛选和切片2.1.1 用谓词筛选2.1.2 筛选各异的元素2.1.3 截短流2.1.4 跳过元素2.2 映射2.2.1 map方法2…...
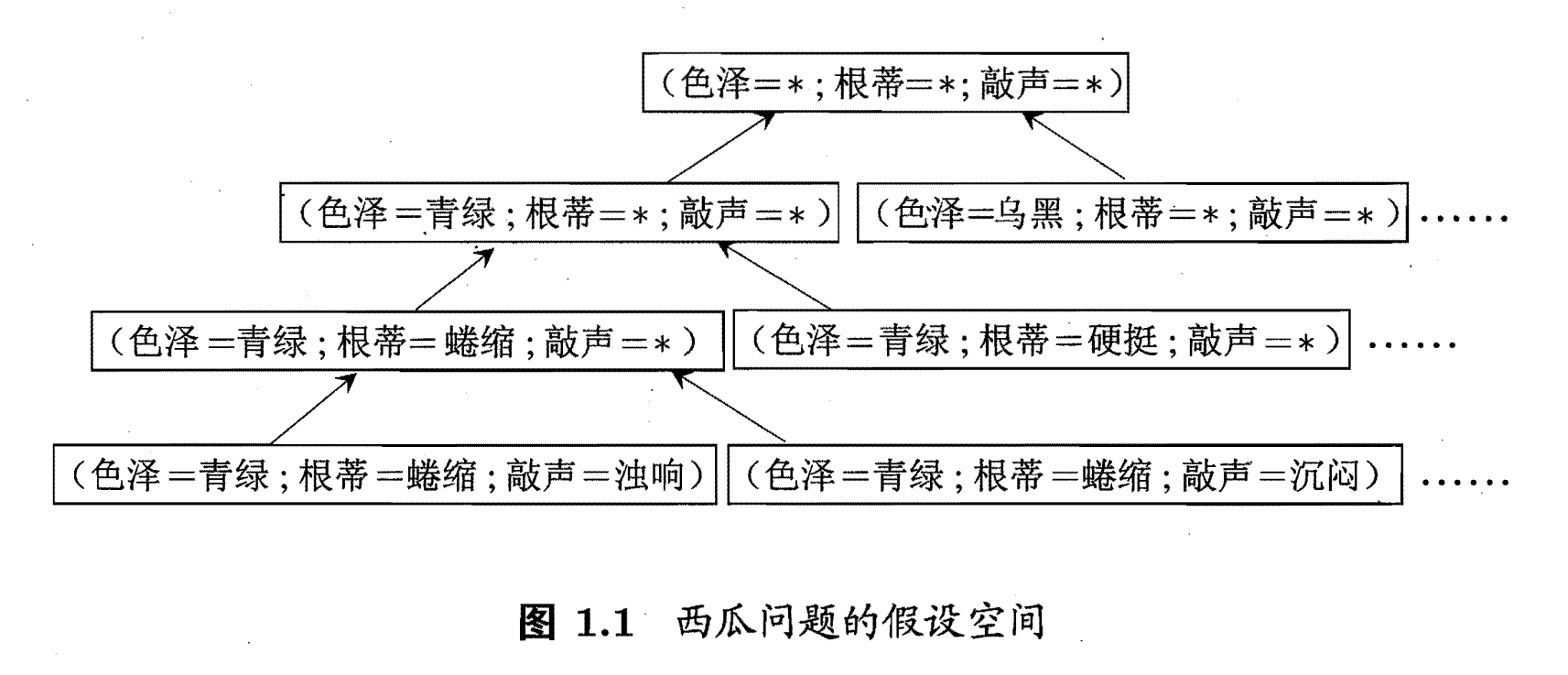
机器学习学习记录1:假设空间
我们可以把学习过程看作一个在所有假设组成的空间中进行搜索的过程,搜索目标是找到与训练集"匹配" 的假设,即能够将训练集中的瓜判断正确的假设.假设的表示一旦确定,假设空间及其规模大小就确定了.对于西瓜问题,这里我们…...
开源工具系列5:DependencyCheck
Dependency-Check 是 OWASP(Open Web Application Security Project)的一个实用开源程序,用于识别项目依赖项并检查是否存在任何已知的,公开披露的漏洞。 DependencyCheck 是什么 Dependency-Check 是 OWASP(Open Web …...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
