深入浅出单调栈与单调队列
目录
- 一、单调栈
- 情形一:寻找一个数左边第一个小于它的数
- 情形二:寻找一个数左边第一个小于它的数的下标
- 情形三:寻找一个数右边第一个大于它的数
- 情形四:寻找一个数右边第一个大于它的数的下标
- 二、单调栈的应用
- 2.1 单调栈模板题I
- 2.2 单调栈模板题II
- 2.3 Bad Hair Day
- 三、单调队列
- 四、单调队列的应用
- 4.1 滑动窗口
一、单调栈
所谓单调栈,就是指满足单调性的栈结构:
- 单调递增栈: 栈中元素从栈底到栈顶是递增的;
- 单调递减栈: 栈中元素从栈底到栈顶是递减的。
例如对于单调递增栈,向其中插入元素的时候,为了维护栈的单调性,需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出最少的元素:
stack<int> stk;void insert(int x) {while (!stk.empty() && stk.top() > x) // 当stk.top() <= x时满足单调性stk.pop();stk.push(x);
}
单调栈可以用来在一个数组中寻找某一个元素左边(或右边)第一个大于(或小于或大于等于或小于等于)它的元素(或元素的下标)。
这句话看起来有些绕,接下来我们只考虑以下四种「基本情形」。
情形一:寻找一个数左边第一个小于它的数
给定一个长度为 n(≤105)n\,(\leq 10^5)n(≤105) 的数组 aaa,输出每个数左边第一个比它小的数,如果不存在则输出 −1-1−1。
传统的暴力做法是双重循环:
#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 10;int a[N];int main() {int n;cin >> n;for (int i = 0; i < n; i++) cin >> a[i];for (int i = 0; i < n; i++) {bool flag = false;for (int j = i - 1; ~j; j--) {if (a[j] < a[i]) {flag = true;cout << a[j] << ' ';break;}}if (!flag) cout << -1 << ' ';}return 0;
}
然而这种做法的复杂度是 O(n2)O(n^2)O(n2),利用单调栈,我们可以将复杂度降低至 O(n)O(n)O(n)。
在指针 iii 从左往右遍历的过程中,我们可以用一个栈来保存 iii 左边的所有元素(不包括 iii 指向的元素),下标越大的元素越接近栈顶,下标越小的元素越接近栈底。
每次我们访问栈顶,只要栈顶元素大于等于 a[i]a[i]a[i],我们就将栈顶元素弹出,直至栈顶元素小于 a[i]a[i]a[i],此时输出栈顶元素并将 a[i]a[i]a[i] 压入栈中。 由于栈中保存了 iii 左边的所有元素,所以只要有答案,则答案一定在栈中。
📃 对证明不感兴趣的读者可以跳过这部分
讲到这里,可能会有读者好奇,栈不是一直在弹出元素吗,万一先前就把答案弹出去了怎么办?这里我们可以从数学的角度进行证明。假设对于 a[i]a[i]a[i],答案一定存在,即∃0≤p<i,s.t.{a[p]<a[i],a[t]>a[p],t=p+1,⋯,i−1\exists\, 0\leq p<i,\quad \text{s.t.}\; \begin{cases} a[p]<a[i], \\ a[t]>a[p], \quad t= p+1,\cdots,i-1 \end{cases} ∃0≤p<i,s.t.{a[p]<a[i],a[t]>a[p],t=p+1,⋯,i−1
对于第二个约束,假设有某个 a[t]≤a[p]a[t]\leq a[p]a[t]≤a[p],那么可知 a[t]<a[i]a[t]<a[i]a[t]<a[i] 并且 a[t]a[t]a[t] 在 a[p]a[p]a[p] 的右边,从而 a[t]a[t]a[t] 才应该是答案,矛盾!
下面证明,当指针指向 a[i]a[i]a[i] 时,a[p]a[p]a[p] 一定存在于栈中。
当指针指向 a[p]a[p]a[p] 时,这一轮循环结束后,a[p]a[p]a[p] 会被压入栈中,所以我们从 p+1p+1p+1 开始考虑。事实上,∀t∈[p+1,i−1]\forall t\in[p+1,i-1]∀t∈[p+1,i−1],当指针指向 a[t]a[t]a[t] 时,无论栈怎么弹出元素,都不会弹出 a[p]a[p]a[p],这是因为栈弹出元素的前提是栈顶元素 ≥a[t]\geq a[t]≥a[t],而 a[p]<a[t]a[p]<a[t]a[p]<a[t] 所以不会被弹出,自然地,当指针指向 a[i]a[i]a[i] 时,a[p]a[p]a[p] 仍在栈中。
由于每个元素一定会被压入一次且至多弹出一次,因此操作次数至多是 2n2n2n,故总时间复杂度为 O(n)O(n)O(n)。
#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 10;int a[N], ans[N];stack<int> stk;int main() {int n;cin >> n;for (int i = 0; i < n; i++) cin >> a[i];for (int i = 0; i < n; i++) {while (!stk.empty() && stk.top() >= a[i]) stk.pop();if (!stk.empty()) ans[i] = stk.top();else ans[i] = -1;stk.push(a[i]);}for (int i = 0; i < n; i++) cout << ans[i] << ' ';return 0;
}
📝 代码完全可以简化,之所以这么写是为了方便统一格式。
情形二:寻找一个数左边第一个小于它的数的下标
和情形一类似,只不过这里我们寻找的是下标,如果不存在则输出 −1-1−1。
只需对栈做一点小小的修改就能应对情形二。注意到之前我们寻找的是元素所以让栈去保存元素,现在我们寻找下标,所以让栈去保存元素的下标就可以了。
#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 10;int a[N], ans[N];stack<int> stk;int main() {int n;cin >> n;for (int i = 0; i < n; i++) cin >> a[i];for (int i = 0; i < n; i++) {while (!stk.empty() && a[stk.top()] >= a[i]) stk.pop(); // 仅有两处修改if (!stk.empty()) ans[i] = stk.top();else ans[i] = -1;stk.push(i); // 仅有两处修改}for (int i = 0; i < n; i++) cout << ans[i] << ' ';return 0;
}
情形三:寻找一个数右边第一个大于它的数
之前我们是在一个数的左边去寻找,所以让栈去保存这个数左边的所有数,类似地,现在需要让栈去保存这个数右边的所有数。
考虑将数组翻转(实际上不可能翻转,而是倒序遍历),因此情形三变成了「寻找一个数左边第一个大于它的数」,于是归结为情形一。
#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 10;int a[N], ans[N];stack<int> stk;int main() {int n;cin >> n;for (int i = 0; i < n; i++) cin >> a[i];for (int i = n - 1; ~i; i--) {while (!stk.empty() && stk.top() <= a[i]) stk.pop();if (!stk.empty()) ans[i] = stk.top();else ans[i] = -1;stk.push(a[i]);}for (int i = 0; i < n; i++) cout << ans[i] << ' ';return 0;
}
情形四:寻找一个数右边第一个大于它的数的下标
结合情形二和情形三即可得出。
#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 10;int a[N], ans[N];stack<int> stk;int main() {int n;cin >> n;for (int i = 0; i < n; i++) cin >> a[i];for (int i = n - 1; ~i; i--) {while (!stk.empty() && a[stk.top()] <= a[i]) stk.pop();if (!stk.empty()) ans[i] = stk.top();else ans[i] = -1;stk.push(i);}for (int i = 0; i < n; i++) cout << ans[i] << ' ';return 0;
}
不难发现,这四种情形只在第 16,17,2016,17,2016,17,20 行不同,其余部分的代码均相同,据此可以总结出以下三点区别:
- 遍历顺序(以怎样的顺序遍历数组 aaa);
- 比较方式(如何比较当前元素和栈顶元素);
- 栈中存储的是什么(是元素本身还是元素的下标还是其他)。
二、单调栈的应用
2.1 单调栈模板题I
原题链接:AcWing 830. 单调栈
此题对应情形一,不再赘述,直接给出AC代码。
#include <bits/stdc++.h>using namespace std;stack<int> stk;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;while (n--) {int x;cin >> x;while (!stk.empty() && stk.top() >= x) stk.pop();if (!stk.empty()) cout << stk.top() << ' ';else cout << -1 << ' ';stk.push(x);}return 0;
}
2.2 单调栈模板题II
原题链接:洛谷 P5788 【模板】单调栈
此题对应情形四,不再赘述,直接给出AC代码。
#include <bits/stdc++.h>using namespace std;const int N = 3e6 + 10;int a[N], ans[N];
stack<int> stk;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = n; i; i--) {while (!stk.empty() && a[stk.top()] <= a[i]) stk.pop();if (!stk.empty()) ans[i] = stk.top();stk.push(i);}for (int i = 1; i <= n; i++) cout << ans[i] << ' ';return 0;
}
2.3 Bad Hair Day
原题链接:POJ 3250 Bad Hair Day
本题类似于情形四,但还是有些区别。
首先应当注意到以下几点:
- 每头牛只向右看;
- 每头牛只能看见比自己低的牛的头顶;
- 若两头牛一样高,则它们互相看不到对方的头顶。
这相当于对数组中的某个数,我们要在它的右边寻找第一个大于等于它的数的下标,知道下标后,我们就可以算出这头牛能够看到多少头牛的头顶了。当然,如果找不到这样的数,说明这头牛的右边全是比它低的牛,此时用牛的数量减去该牛的下标(从 111 开始)就是该牛能够看到的头顶的数量。
还需注意一个问题,假设给定的序列是单调递减的,那么所求答案为 N(N−1)/2≈3×109N(N-1)/2\approx 3\times 10^9N(N−1)/2≈3×109,会爆 int。
#include <stack>using namespace std;typedef long long LL;LL h[80010], ans;
stack<LL> stk;int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; i++) scanf("%lld", &h[i]);for (int i = n; i; i--) {while (!stk.empty() && h[stk.top()] < h[i]) stk.pop();if (!stk.empty()) ans += stk.top() - i - 1;else ans += n - i;stk.push(i);}printf("%lld", ans);return 0;
}
三、单调队列
单调队列的定义类似于单调栈:
- 单调递增队列: 从队尾到队头单调递增;
- 单调递减队列: 从队尾到队头单调递减。
例如对于单调递增队列,向其中插入元素的时候,为了维护队列的单调性,需要在保证将该元素插入到队尾后整个队列满足单调性的前提下弹出最少的元素(从队尾弹出):
deque<int> q; // 因为涉及到从队尾弹出,所以只能用双端队列来实现单调队列void insert(int x) {while (!q.empty() && q.back() < x)q.pop_back();q.push_back(x);
}
⚠️ 严格意义上讲单调队列并不是队列,因为它不满足FIFO。
四、单调队列的应用
4.1 滑动窗口
原题链接:AcWing 154. 滑动窗口
单调队列常用于求滑动窗口中的最大(小)值。我们先来看一下这道题的暴力解法是什么样的:
#include <bits/stdc++.h>using namespace std;typedef long long LL;const LL INF = 3e9;LL a[1000010];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, k;cin >> n >> k;for (int i = 0; i < n; i++) cin >> a[i];for (int i = 0; i <= n - k; i++) {LL mini = INF;for (int j = i; j < i + k; j++) mini = min(mini, a[j]);cout << mini << ' ';}cout << "\n";for (int i = 0; i <= n - k; i++) {LL maxi = -INF;for (int j = i; j < i + k; j++) maxi = max(maxi, a[j]);cout << maxi << ' ';}return 0;
}
显然时间复杂度为 O(nk)O(nk)O(nk),基本会TLE。使用单调队列,我们可以将时间复杂度降低至 O(n)O(n)O(n)。
以求最小值为例,我们使用单调递减队列来保存滑动窗口中的元素,下标越大的元素越接近队尾,下标越小的元素越接近队头,于是求滑动窗口中的最小值相当于访问队头元素。
不妨设下标从 111 开始,初始时 iii 指向 111,并且 iii 从 111 遍历至 nnn,每次遍历都将 a[i]a[i]a[i] 插入到队列中。可以发现,只要有 i<ki< ki<k 就说明滑动窗口还未形成,此时无需输出最小值,当 i≥ki\geq ki≥k 时才需要输出最小值。
那何时弹出队头元素呢?不妨让单调队列保存的是元素的下标而非元素本身,设当前窗口为 a[i−k..i−1]a[i-k..i-1]a[i−k..i−1],向单调队列插入 iii 后,新窗口变成 a[i−k+1..i]a[i-k+1..i]a[i−k+1..i],如果队头元素小于等于 i−ki-ki−k,说明最小值不在新窗口中,此时应当弹出队头元素。
到目前为止,可以总结出两点:
- 只要 i≥ki\geq ki≥k 就应当输出队头元素;
- 当队头元素小于等于 i−ki-ki−k 时,弹出队头元素。
#include <bits/stdc++.h>using namespace std;const int N = 1e6 + 10;int a[N];
deque<int> q;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, k;cin >> n >> k;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = 1; i <= n; i++) {while (!q.empty() && a[q.back()] > a[i]) q.pop_back();q.push_back(i);if (!q.empty() && q.front() <= i - k) q.pop_front(); // 既可以用if也可以用whileif (i >= k) cout << a[q.front()] << ' ';}cout << "\n";q.clear();for (int i = 1; i <= n; i++) {while (!q.empty() && a[q.back()] < a[i]) q.pop_back();q.push_back(i);if (!q.empty() && q.front() <= i - k) q.pop_front(); // 既可以用if也可以用whileif (i >= k) cout << a[q.front()] << ' ';}return 0;
}
此题还可以用优先队列来做,为避免不必要的判断,我们可以在一开始就向队列中插入前 kkk 个元素:
#include <bits/stdc++.h>using namespace std;typedef pair<int, int> PII;
const int N = 1e6 + 10;int a[N];
priority_queue<PII> p; // 大根堆
priority_queue<PII, vector<PII>, greater<>> q; // 小根堆int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, k;cin >> n >> k;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = 1; i <= k; i++) q.emplace(a[i], i);cout << q.top().first << ' ';for (int i = k + 1; i <= n; i++) {q.emplace(a[i], i);while (!q.empty() && q.top().second <= i - k) q.pop(); // 只能用whilecout << q.top().first << ' ';}cout << "\n";for (int i = 1; i <= k; i++) p.emplace(a[i], i);cout << p.top().first << ' ';for (int i = k + 1; i <= n; i++) {p.emplace(a[i], i);while (!p.empty() && p.top().second <= i - k) p.pop(); // 只能用whilecout << p.top().first << ' ';}return 0;
}
观察上面两段代码,可以发现思路是大致相同的,但区别在于(请看注释行),单调队列在弹出队头元素的时候既可以用 if 也可以用 while,而优先队列弹出队头元素的时候只能用 while,这是为什么呢?
考虑数组 [4,6,2,3,5,1,8,7,9][4,6,2,3,5,1,8,7,9][4,6,2,3,5,1,8,7,9],窗口大小为 333,以求最小值为例,每次循环结束后单调队列和优先队列的状态列在下表中:
⚠️ 列表的左端是队头,右端是队尾。
⚠️ 对于优先队列,只需看列表的第一个元素,其后元素的次序无关紧要。
| 滑动窗口 | 单调队列 | 优先队列 |
|---|---|---|
| [4,6,2][4,6,2][4,6,2] | [2][2][2] | [2,4,6][2,4,6][2,4,6] |
| [6,2,3][6,2,3][6,2,3] | [2,3][2,3][2,3] | [2,4,6,3][2,4,6,3][2,4,6,3] |
| [2,3,5][2,3,5][2,3,5] | [2,3,5][2,3,5][2,3,5] | [2,4,6,3,5][2,4,6,3,5][2,4,6,3,5] |
| [3,5,1][3,5,1][3,5,1] | [1][1][1] | [1,2,4,6,3,5][1,2,4,6,3,5][1,2,4,6,3,5] |
| [5,1,8][5,1,8][5,1,8] | [1,8][1,8][1,8] | [1,2,4,6,3,5,8][1,2,4,6,3,5,8][1,2,4,6,3,5,8] |
| [1,8,7][1,8,7][1,8,7] | [1,7][1,7][1,7] | [1,2,4,6,3,5,8,7][1,2,4,6,3,5,8,7][1,2,4,6,3,5,8,7] |
| [8,7,9][8,7,9][8,7,9] | [7,9][7,9][7,9] | [7,8,9][7,8,9][7,8,9] |
因为优先队列在插入元素的过程中不会弹出元素,所以只要队头位于窗口内,那么优先队列的大小只增不减,这就导致优先队列中存在许多冗余元素(不属于窗口内的元素)。而单调队列为了保持单调性,插入元素的时候会从队尾弹出一些元素,这就保证了单调队列中的元素始终是滑动窗口中的元素的子集,因此单调队列的 while 循环至多执行一次,自然可以改成 if。
相关文章:

深入浅出单调栈与单调队列
目录一、单调栈情形一:寻找一个数左边第一个小于它的数情形二:寻找一个数左边第一个小于它的数的下标情形三:寻找一个数右边第一个大于它的数情形四:寻找一个数右边第一个大于它的数的下标二、单调栈的应用2.1 单调栈模板题I2.2 单…...

深入C语言——实现可变参数函数
文章目录初步示例函数解析最大值函数初步示例 stdarg.h提供了C语言对可变参数的支持,先举一个简短的例子 //testStdArg.c #include <stdarg.h> #include <stdio.h>void printIntList(int N, ...){va_list args; //存放...所代表的参数va_start(…...

41-Dockerfile-Dockerfile简介
Dockerfile简介前言Dockerfile 简介基础知识使用Dockerfile 构建镜像步骤Dockerfile 构建过程Dockerfile基本结构Dockerfile示例总结前言 本篇开始来学习下Dockerfile相关的用法 Dockerfile 简介 Dockerfile : 是用来构建 Docker 镜像的文本文件,是有一条条构建镜…...
【408】操作系统 - 刻骨铭心自测题1(上)
文章目录OS练习题第一部分:1:2:3:4:5:6:7:8:9:10:11:12:13:14:15:16:17&am…...

【老卫拆书】009期:Vue+Node肩挑全栈!《Node.js+Express+MongoDB+Vue.js全栈开发实战》开箱
今天刚拿到一本新书,叫做《Node.jsExpressMongoDBVue.js全栈开发实战》,做个开箱。 外观 先从外观上讲,这本是全新的未开封的,膜还在。 这本书介绍从技术原理到整合开发实战,以丰富的项目展现全栈开发的一个技巧。 …...
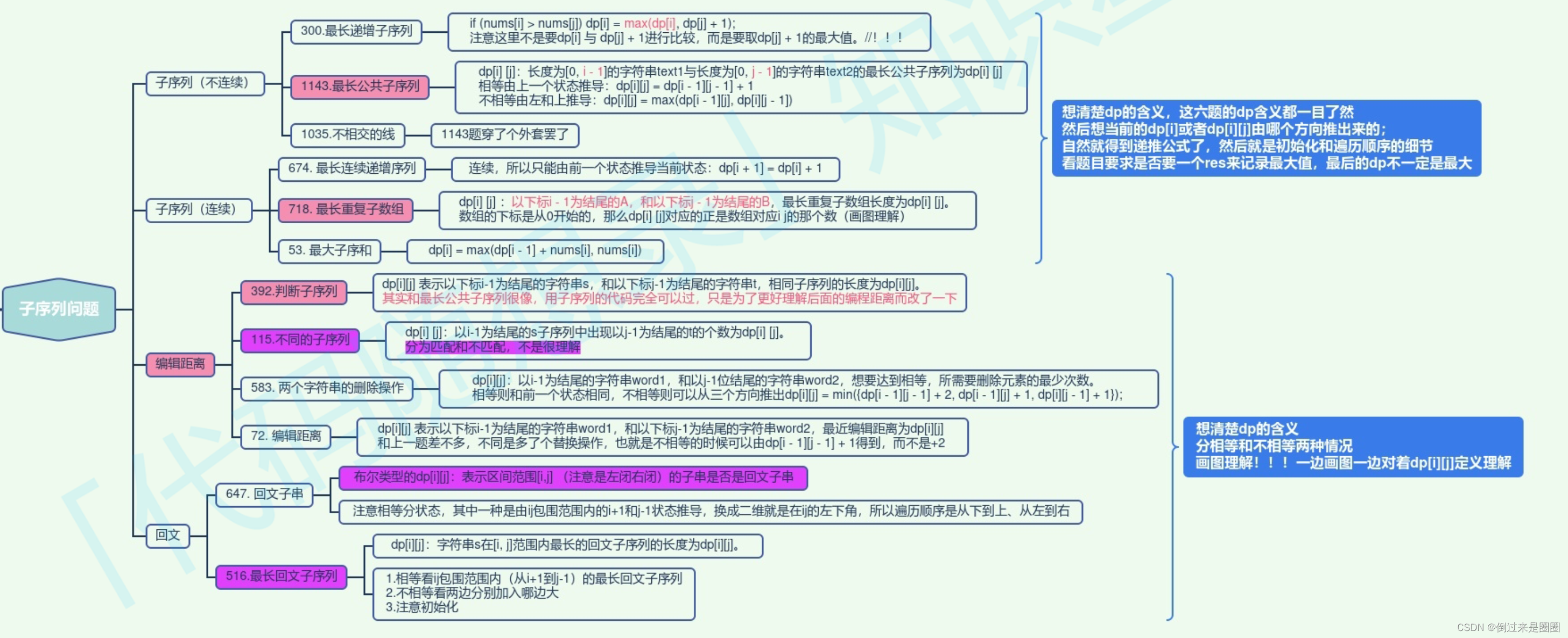
【LeetCode】动态规划总结
动态规划解决的问题 动态规划和贪心的区别: 动态规划是由前一个状态推导出来的; 贪心是局部直接选最优的。 动态规划解题步骤 状态定义:确定dp数组以及下标的含义状态转移方程:确定递推公式初始条件:dp如何初始化遍历…...

CAS详解.
CAS这个机制就给实现线程安全版本的代码,提供了一个新的思路,之前通过加锁,把多个指令打包成整体,来实现线程安全。现在就可以考虑直接基与CAS来实现一些修改操作,也能保证线程安全(不需要加锁)…...
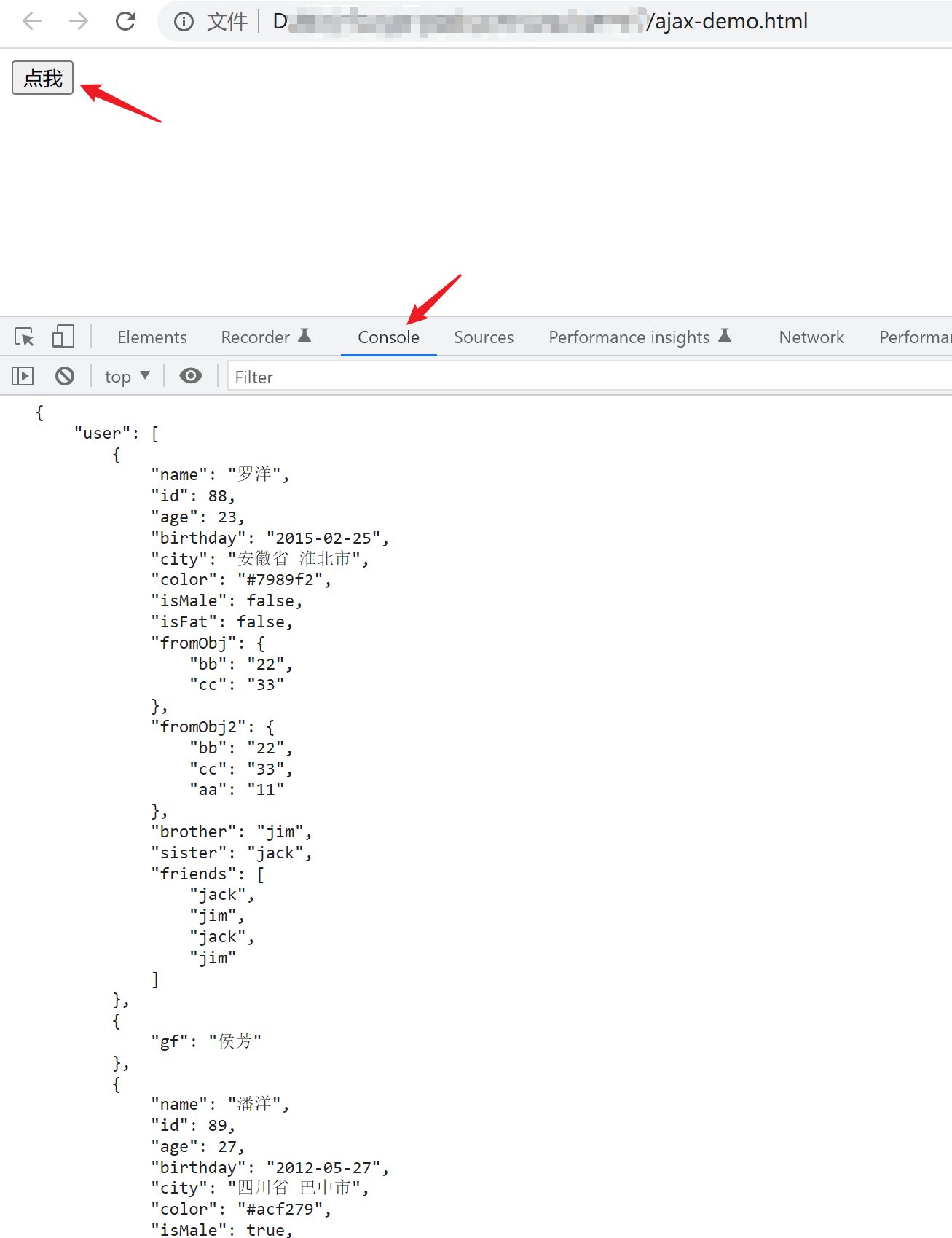
Mock.js初步使用(浏览器端)
Mock.js:生成随机数据,拦截 Ajax 请求。官方地址:http://mockjs.com/第一个demodemo.html<!DOCTYPE html> <html> <head><meta charset"utf-8"><title>mockjs demo</title> </head> <…...

opencv保存图片
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...
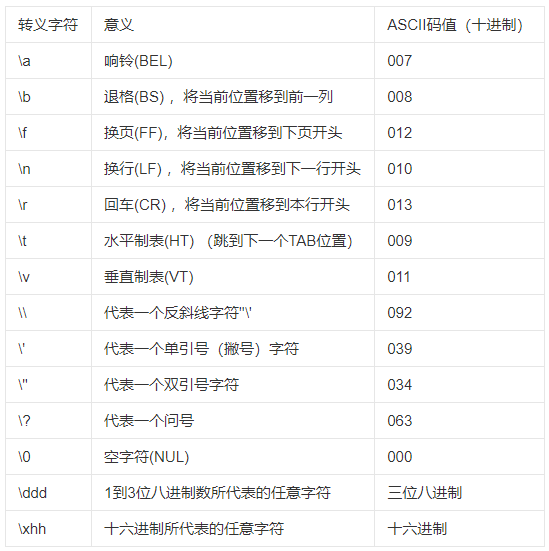
【c++】数据类型
文章目录整型实型科学计数法sizeof关键字字符型字符串类型转义字符bool布尔类型c规定在创建一个变量或者常量时,必须要指定出相应的数据类型,否则无法给变量分配内存。 整型 作用:整型变量表示的是整数类型的数据。 实型 float f3.14; //默…...

Elasticsearch的写的底层原理
前面有一篇文章讲解了Elasticsearch的读写搜索过程,有的人感觉不太理解,今天我们再来看看这些过程的原理 写数据底层原理 首先是将数据写入到内存buffer中,在这里的时候,数据是搜索不到。他同时会将数据写入到translog日志文件中…...

【网络编程】Java中的Socket
文章目录前言socket是什么?Java中的SocketJava实现网络上传文件前言 所谓Socket(套接字),就是对网络中不同主机上的应用进程之间进行双向通信的端点的抽象。一个套接字就是网络上进程通信的一端,提供了应用层进程利用…...
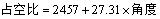
有趣的Hack-A-Sat黑掉卫星挑战赛——跟踪卫星
国家太空安全是国家安全在空间领域的表现。随着太空技术在政治、经济、军事、文化等各个领域的应用不断增加,太空已经成为国家赖以生存与发展的命脉之一,凝聚着巨大的国家利益,太空安全的重要性日益凸显[1]。而在信息化时代,太空安…...
Ubuntu安装配置Cuda和Pytorch gpu
前言 在Ubuntu中操作系统中,通过Anconda安装对应的虚拟环境以及软件包,一般都需要适配Cuda、Pytorch版本等 以下安装配置都是在Ubuntu操作系统下 1. 安装Cuda 通过Ubuntu操作系统查看cuda适配的版本:nvidia-smi 截图如下: 查看Ubuntu版本可如下方式 (1)cat /proc/ver…...

三、Java面向对象
1 . 方法 方法(method)是程序中最小的执行单元方法就是一些代码的打包 需要的时候可以直接调用方法之间是平级的关系 不能在方法里面定义方法方法不调用就不执行 方法的定义 // 方法的定义 /* [修饰符] 返回值类型 方法名称([参数 1],[参数 2]){语句A;return 返回值; } *///…...

pygame7 弹球游戏2
上节课我们做到当球静止下来后在第0号球上画一个球杆 本节课我们将会让这个球杆将球打出来 1、鼠标事件 pygame.mouse.get_pressed():返回鼠标左键,中间,右键的情况 2、键盘事件: pygame.key.get_pressed(): 返回所有键盘的情况 3、pyg…...
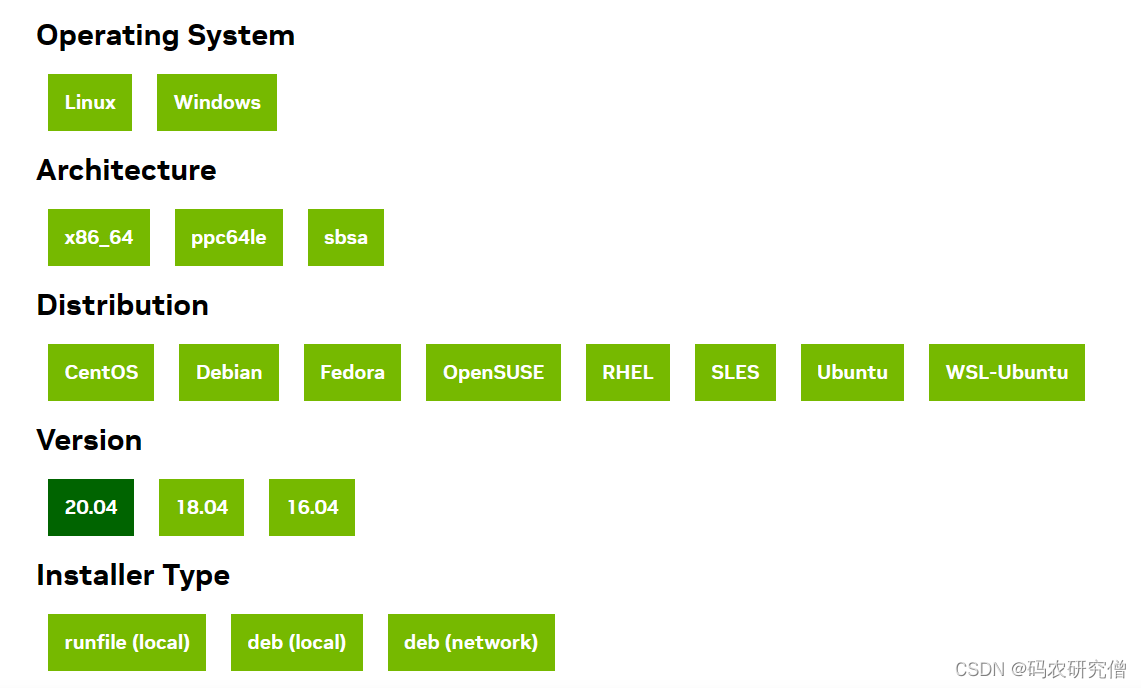
计算机网络4:计算机网络体系结构
目录计算机网络体系结构1.网络模型2.每一层的代表含义2.1 OSI7层模型2.2 五层协议2.3 TCP/IP 四层协议3.数据在各层之间的传输过程4.为什么要进行分层计算机网络体系结构 1.网络模型 2.每一层的代表含义 2.1 OSI7层模型 (1)物理层:比特流–…...

1630_GNU的二进制分析工具nm简单使用探索
全部学习汇总: GreyZhang/toolbox: 常用的工具使用查询,非教程,仅作为自我参考! (github.com) GNU有一套二进制的分析工具,之前是用过objdump的,但是也没有系统掌握。如果做底层软件的设计,这些…...
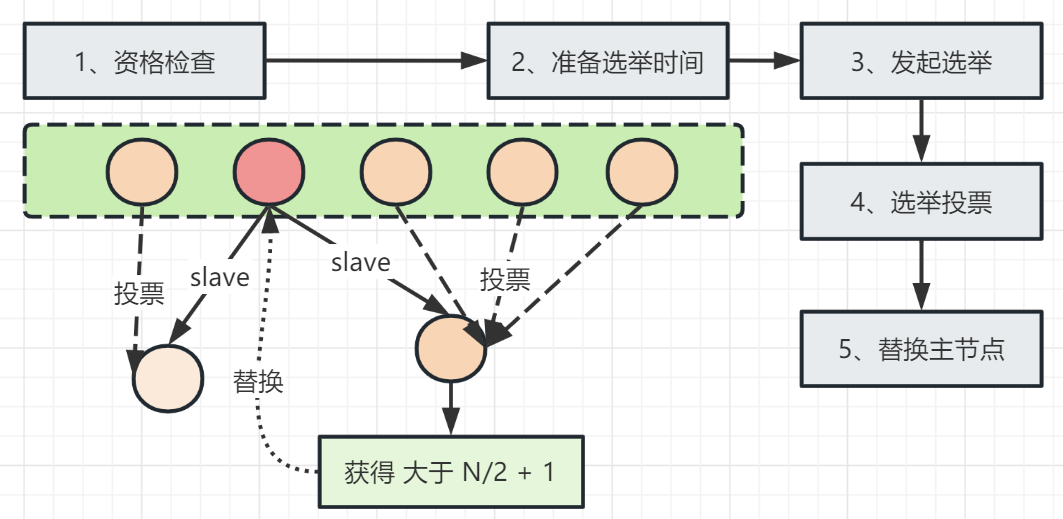
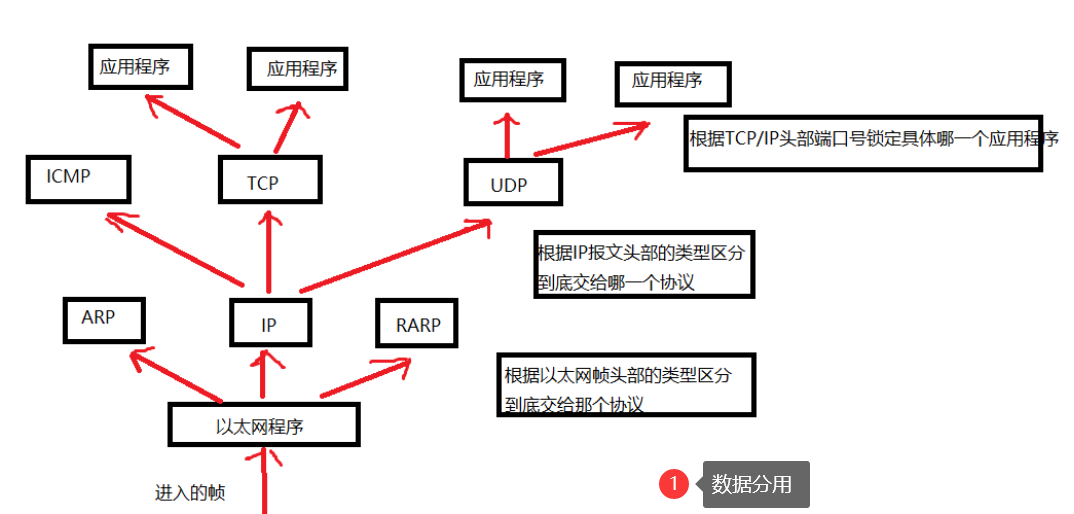
【Redis】Redis高可用之Redis Cluster集群模式详解(Redis专栏启动)
📫作者简介:小明java问道之路,2022年度博客之星全国TOP3,专注于后端、中间件、计算机底层、架构设计演进与稳定性建工设优化。文章内容兼具广度深度、大厂技术方案,对待技术喜欢推理加验证,就职于知名金融公…...
1.8 正则表达式
正则表示式是用来匹配与查找字符串的,从网上爬取数据不可避免的会用到正则表达式。 Python 的表达式要先引入 re 模块,正则表达式以 r 引导。Re库主要功能函数函数说明re.search()在一个字符串中搜索匹配正则表达式的第一个位置,返回match对象…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
