图----无向图
1.定义
图的定义:图是由一组顶点和一组能够将两个顶点相连的边组成
边:edge
顶点:vertex
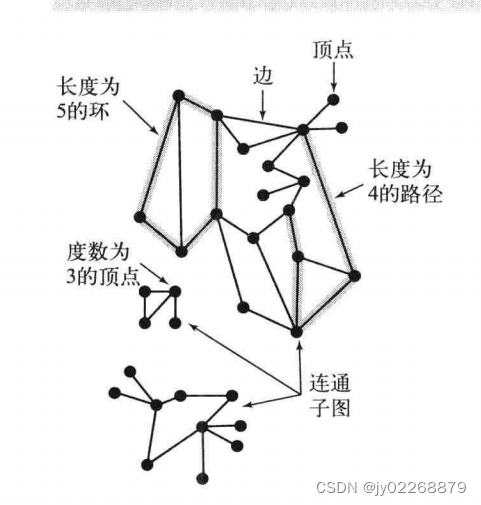
连通图:如果从任意一个顶点都存在一条路径到达另外一个任意顶点,我们称这幅图是连通图。
非连通图:由若干连通的部分组成,他们都是其极大连通子图。
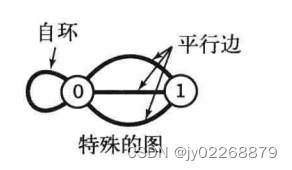
自环:即一条连接一个顶点和其自身的边
平行边:连接同一顶点的两条边称为平行边
图的密度:是指已经连接的顶点对占所有可能被连接的顶点对的比例。在稀疏图中,被连接的顶点对很少;而在稠密图中,只有少部分顶点对之间没有边连接。

二分图:是一种能够将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。
2.图的不同表示方法
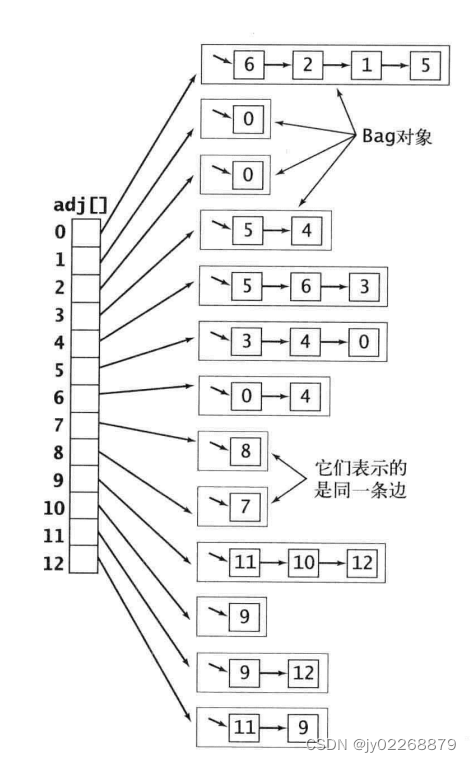
2.1邻接表数组表示
用一个以顶点为索引的列表数组,其中的每个元素都是和该顶点相邻的定点列表
2.2邻接矩阵 表示
用一个V乘以V的布尔矩阵。当顶点V和顶点W之间有相连的边时,定义V行W列的元素值为true,否则为false。如果含有上百万个顶点,V的平方个布尔值所需要的空间会非常大。
3.相关API及代码


package com.sid.graph;public class Vertex {String value;//顶点的值Edge firstEdge;//第一条边int index;//在外层数组的下标public Vertex(String value, Edge firstEdge,int index) {super();this.value = value;this.firstEdge = firstEdge;this.index = index;}
}
package com.sid.graph;public class Edge {Vertex vertex;//该边对应的顶点int weight;//权重,无向图,有向图权重为0Edge next;//下一个边/*** 构建一条边 weight未0表示无向图或者有向图 不为0表示网* @param vertex* @param weight* @param next*/public Edge(Vertex vertex, int weight, Edge next) {super();this.vertex = vertex;this.weight = weight;this.next = next;}
}
package com.sid.graph;import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;public class Graph {/*** 顶点数*/private final int V;/*** 边数*/private int E;/*** 邻接表*/private List<Vertex> adj;public Graph(int V) {this.V = V;this.E = 0;adj = new ArrayList<Vertex>(V); /** 创建邻接表 */}public int V() {return V;}public int E() {return E;}/*** 插入顶点*/public Vertex addVertex(String value) {int size = adj.size();Vertex vertex = new Vertex(value, null,size);adj.add(vertex);return vertex;}/*** 获取顶点*/public Vertex getVertexByValue(String value) {for (int i = 0; i < V; i++) {if (adj.get(i).value.equals(value)) {return adj.get(i);}}return null;}/*** 获取顶点*/public Vertex getVertexByIndex(int index) {return adj.get(index);}/*** 添加无向图的边* @param vertex1 第一个顶点* @param vertex2 第二个顶点*/public void addUndigraphEdge(Vertex vertex1,Vertex vertex2) {//因为是无向图,所以就直接加入addEdgeByVertex(vertex1,vertex2,0);addEdgeByVertex(vertex2,vertex1,0);}/*** 添加有向图的边* @param start 开始节点* @param end 结束节点*/public void addDigraphEdge(Vertex start,Vertex end) {//因为是有向图,所以只有一条边addEdgeByVertex(start,end,0);}/*** 添加一条由start-->end的边** @param start* @param end* @param weight 权重未0表示无向图或者有向图,部位0表示网*/private void addEdgeByVertex(Vertex start, Vertex end, int weight) {//1、找到第一个顶点Vertex v1 = this.getVertexByValue(start.value);if(v1 == null){v1 = addVertex(start.value);}//2、检查这条边是否已经存在,已经存在就直接报错for (Vertex w : adj(v1)) {if (end.value.equals(w.value)) {System.out.println("边" + start.value + "-->" + end.value + "已经加入,不可以再加入");return;}}//3.添加Edge firstEdge = v1.firstEdge;if (firstEdge == null) {firstEdge = new Edge(end, weight, null);v1.firstEdge = firstEdge;} else {//当前节点变为第一个节点Edge nowEdge = new Edge(end, weight, null);v1.firstEdge = nowEdge;nowEdge.next = firstEdge;}E++;}/*** 计算V节点的度数*/public static int degree(Graph g, int v) {int degree = 0;Edge firstEdge = g.getVertexByIndex(v).firstEdge;while (firstEdge != null) {degree++;firstEdge = firstEdge.next;}return degree;}/*** 计算所有顶点的最大度数*/public static int maxDegree(Graph G) {int max = 0;for (int v = 0; v < G.V(); v++) {if (degree(G, v) > max) {max = degree(G, v);}}return max;}/*** 计算所有顶点的平均度数*/public static int avgDegree(Graph G) {return 2 * G.E() / G.V();}/*** 计算自环的的个数*/public static int numberOfSelfLoops(Graph g) {int count = 0;for (int v = 0; v < g.V(); v++) {for(int w : g.adj(v)){if(v == w){count++;}}}return count / 2; //每条边都被记过两次}/*** 得到跟V节点相邻的所有节点*/public static List<Vertex> adj(Vertex vertex) {List result = new LinkedList();Edge firstEdge = vertex.firstEdge;while (firstEdge != null) {result.add(firstEdge.vertex);firstEdge = firstEdge.next;}return result;}/*** 得到跟V节点相邻的所有节点下标 入参是节点的数组下标*/public List<Integer> adj(int index) {List result = new ArrayList();Edge firstEdge = this.getVertexByIndex(index).firstEdge;while (firstEdge != null) {result.add(firstEdge.vertex.index);firstEdge = firstEdge.next;}return result;}/*** 图的邻接表的字符串表示*/public String toString() {String s = V + " vertices, " + E + " edges\n";for (int v = 0; v < V; v++) {Vertex vertex = this.getVertexByIndex(v);s += vertex.value + ": ";for (Vertex w : adj(vertex)) {s += w.value + "";}s += "\n";}return s;}
}
4.深度优先搜索
4.1 找到以起点s连通的所有顶点,和个数
实现:
用一个递归方法来遍历所有顶点,在访问一个顶点时:
将它标记为已访问
递归地访问它的所有没有被标记过的邻居顶点

package com.sid.graph;public class DepthFirstSearch {private boolean[] marked;private int count;public DepthFirstSearch(Graph G,int s){marked = new boolean[G.V()];dfs(G,s);}private void dfs(Graph G, int index) {marked[index] = true;count++;for(int w : G.adj(index)){if(!marked[w]){dfs(G,w);}}}public boolean marked(int w ){return marked[w];}public int count(){return count;}
}
4.2深度优先搜索查找图中路径

注意这不一定是最短路径,比如说下面这个例子,查出来的0到1的路径,不是0----1,而是0----2----1

package com.sid.graph;import java.util.Stack;public class DepthFirstPaths {private boolean[] marked; //这个顶点上调用过dfs()了吗private int[] edgeTo; //从起点到一个顶点的已知路径上的最后一个顶点 比如S---A---C 则 edgeTo[C]=A edgeTo[C]其实表示的是谁直接指向C点private final int s; //起点public DepthFirstPaths(Graph G, int s) {marked = new boolean[G.V()];edgeTo = new int[G.V()];this.s = s;dfs(G, s);}private void dfs(Graph G, int index) {marked[index] = true;for (int w : G.adj(index)) {if (!marked[w]) {edgeTo[w] = index;dfs(G, w);}}}public boolean hasPathTo(int v){ //起点S是否有路径到Vreturn marked[v];}public Iterable<Integer> pathTo(int v){if(!hasPathTo(v)){return null;}Stack<Integer> path = new Stack<Integer>();for(int x = v ; x != s ; x = edgeTo[x]){path.push(x);}path.push(s);return path;}
}
5.广度优先搜索
深度优先搜索得到的路径不仅取决于图的结构,还取决于图的表示和递归调用的性质。
“从S到给定目标的顶点V是否存在一条路径?如果有,找出其中最短的那条”,则需要用广度优先搜索。
实现:
1.使用一个队列来保存所有已经被标记过,但其邻接表还未被检查过的顶点
2.先将起点加入队列,然后重复以下步骤直到队列为空
取队列中的下一个顶点v并标记它
将与v相邻的所有未被标记过的顶点加入队列

package com.sid.graph;import java.util.*;public class BreadthFirstPaths {private boolean[] marked; //这个顶点上调用过dfs()了吗private int[] edgeTo; //从起点到一个顶点的已知路径上的最后一个顶点 比如S---A---C 则 edgeTo[C]=A edgeTo[C]其实表示的是谁直接指向C点private final int s; //起点public BreadthFirstPaths(Graph G, int s) {marked = new boolean[G.V()];edgeTo = new int[G.V()];this.s = s;bfs(G, s);}private void bfs(Graph G, int s) {Queue<Integer> queue = new PriorityQueue<>();marked[s] = true;queue.add(s);while (!queue.isEmpty()){int v = queue.poll();for(int w : G.adj(v)){if(!marked[w]){edgeTo[w] = v;marked[w] = true;queue.add(w);}}}}public boolean hasPathTo(int v){return marked[v];}public Iterable<Integer> pathTo(int v){if(!hasPathTo(v)){return null;}Stack<Integer> path = new Stack<Integer>();for(int x = v ; x != s ; x = edgeTo[x]){path.push(x);}path.push(s);return path;}
}
6.连通分量
无向图G的极大连通子图称为G的连通分量( Connected Component)。
任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。

实现
使用marked[]数组来寻找一个顶点作为每个连通分量中深度优先搜索的起点。
递归的深度优先搜索第一次调用的参数是顶点0,它会标记所有与0连通的顶点。
然后构造函数中for循环会查找每个没有被标记的顶点,并且递归调用dfs()来标记和它相邻的所有顶点。
使用一个以顶点作为索引的数组id[],将同一个连通分量的顶点和连通分量的标识符关联起来(int 值)。这个数组是的connected()方法的实现变得十分简单。
标识符0会被赋予第一个连通分量中的所有顶点,1会被赋予第二个连通分量中的所有顶点,以此类推。这样所有的标识符都会如API中指定的那样在0到count()-1之间。这个约定使得以子图作为索引的数组成为可能。
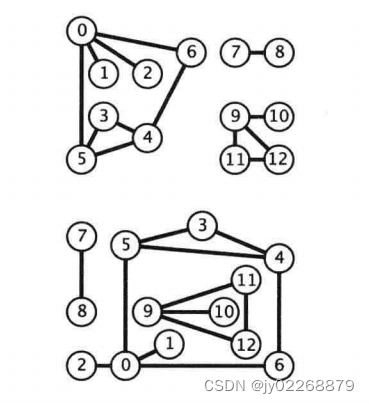
例子

最后
id[0]= 0
id[1]= 0
id[2]= 0
id[3]= 0
id[4]= 0
id[5]= 0
id[6]= 0
id[7]= 1
id[8]= 1
id[9]= 2
id[10]= 2
id[11]= 2
id[12]= 2
也就是说count[]的值相同的是一个连通分量,count[]的值不同的节点之间是走不通的。
代码
package com.sid.graph;public class CC {private boolean[] marked;private int[] id;private int count;public CC(Graph G){marked = new boolean[G.V()];id = new int[G.V()];for(int s = 0 ; s < G.V(); s++){if(!marked[s]){dfs(G,s);count++;}}}private void dfs(Graph G,int v){marked[v] = true;id[v] = count;for(int w : G.adj(v)){if(!marked[w]){dfs(G,w);}}}public boolean connected(int v, int w){return id[v] == id[w];}public int id(int v){return id[v];}public int count(){return count;}
}
7.G是无环图吗
使用深度优先处理
如果不存在自环和平行边,就是无环图
package com.sid.graph;public class Cycle {private boolean[] marked;private boolean hasCycle;public Cycle(Graph G){marked = new boolean[G.V()];for(int s = 0 ; s < G.V(); s++){if(!marked[s]){dfs(G,s,s);}}}private void dfs(Graph G, int v , int u){marked[v] = true;for(int w : G.adj(v)){if(!marked[w]){dfs(G,w,v);}else if(w != u){ //A---B 与B相邻的节点肯定有A,我理解的是无向图中他们属于同一条边,不是环。hasCycle = true;}}}public boolean hasCycle(){return hasCycle;}
}
8.G是二分图吗(双色问题)
package com.sid.graph;public class TwoColor {private boolean[] marked;private boolean[] color;private boolean isTowColorable = true;public TwoColor(Graph G){marked = new boolean[G.V()];color = new boolean[G.V()];for(int s = 0 ; s < G.V(); s++){if(!marked[s]){dfs(G,s);}}}private void dfs(Graph G, int v) {marked[v] = true;for (int w : G.adj(v)){if(!marked[w]){color[w] = !color[v];}else if(color[w] == color[v]){isTowColorable = false;return;}}}public boolean isBipartite(){return isTowColorable;}
}
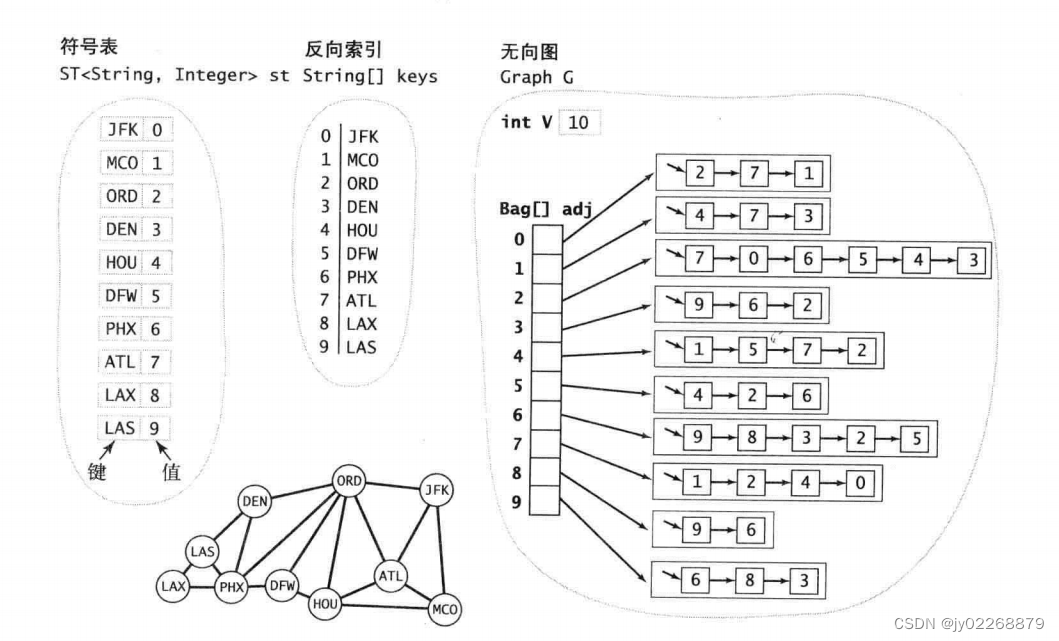
9.符号图
节点里面装的不是数字,而是其他的,比如字符串

相关文章:

图----无向图
1.定义 图的定义:图是由一组顶点和一组能够将两个顶点相连的边组成 边:edge 顶点:vertex 连通图:如果从任意一个顶点都存在一条路径到达另外一个任意顶点,我们称这幅图是连通图。 非连通图:由若干连通的…...
【C++1】函数重载,类和对象,引用,/string类,vector容器,类继承和多态,/socket,进程信号
文章目录1.函数重载:writetofile(),Ctrue和false,C0和非02.类和对象:vprintf构造函数:对成员变量初始化析构函数:一个类只有一个,不允许被重载3.引用:C中&取地址,C中…...
JetpackCompose从入门到实战学习笔记8—ConstraintLayout的简单使用
JetpackCompose从入门到实战学习笔记8—ConstraintLayout的简单使用 1.简介: Compose 中的 ConstraintLayout ConstraintLayout 是一种布局,让您可以相对于屏幕上的其他可组合项来放置可组合项。它是一种实用的替代方案,可代替使用多个已嵌…...

Spring Boot 快速入门(绝对经典)
目录 1、理论概述 1.1、什么是Spring Boot? 1.2、Spring Boot的特点 1.3、开发环境 2、实战——创建和配置项目 2.1、Spring Boot项目创建的两种方式 2.1.1、方法一:通过网站构建项目 2.1.2、使用Spring Initializr创建(推荐) 2.2、…...

golang context上下文
文章目录一、为什么需要context二、context 接口三、Background 方法四、 with 系列函数1、WithCancel 方法2、WithDeadline 方法3、WithTimeout 方法4、WithValue 方法五、使用注意事项一、为什么需要context 在 Go http包的Server中,每一个请求在都有一个对应的 …...
Linux---Linux是什么
Linux 便成立的核心网站: http://www.kernel.org Linux是什么 Linux 就是一套操作系统 Linux 就是核心与系统呼叫接口那两层 软件移植:如果能够参考硬件的功能函数并据以修改你的操作系统程序代码, 那经过改版后的操作系统就能够在另一个硬…...

C语言(Tgmath.h库(C99),exit和atexit)
一.Tgmath.h库(C99) C99标准提供得tgmath.h头文件定义了泛型类型宏。比如在math.h中为一个函数定义了3中类型(float,double和long double)的版本,那么tgmath.h文件就创建一个泛型类型宏,与原来的float,double和long double版本的…...

LeetCode 刷题系列 -- 739. 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。示例 1:输入:temperatures …...
如何生成毕业论文的目录和创建模板
有粉丝同学最近在写毕业论文,其中比较让人恼火的是毕业论文的目录,折腾了几遍没弄好,想让我写个简单地教程,那就来吧。主要分为三步:第一步是从模板里面提取标题的样式,第二步是对自己的论文使用设置好的标…...

新来的23岁软件测试员上来秀了波操作,把几个老员工看傻了
春招了,公司来了个小伙子,一看简历,嘿?22岁,这不刚毕业的小毛孩子嘛,结果没想到人家上来就把现有项目的性能优化了一遍,给公司节省了一半的成本,这种“王炸”打法,直接给…...
Window10开放某个端口
需求:由于防火墙原因,开放某个端口:如9999 在开始那里搜索防火墙-进入防火墙 第一步:核实是否启动了防火墙,之后进行 第二步:点击“高级设置”,→“入站规则”→“新建规则”→“端口”→ “下一步” …...

进阶7 分页查询
进阶7 分页查询!!! 目录概述练习题概述 应用场景:当要显示的数据一页显示不全,需要分页提交SQL请求 语法: select 查询列表 from 表名 【join type join 表2 on 连接条件 where 筛选条件 group by 分组字段…...

利用升序定时器链表处理非活动连接
参考自游双《Linux高性能服务器编程》 背景 服务器同常需要定期处理非活动连接:给客户发一个重连请求,或关闭该连接,或者其他。我们可以通过使用升序定时器链表处理非活动连接,下面的代码利用alarm函数周期性的触发SIGALRM信号&a…...

MySQL 开发规范
一、数据库命名规范所有数据对象名称必须小写 :db_user禁止使用MySQL 保留关键字,若是则引用 临时表以tmp_ 开头,备份表以bak_ 开头并以时间戳结尾所有存储相同数据的列名和列类型必须一致二、数据库基本设计规范1、MySQL…...
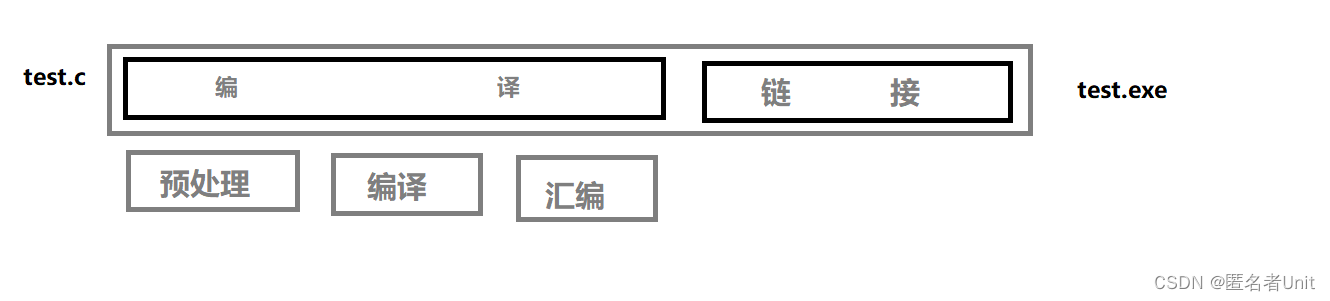
【C语言进阶】预处理与程序环境
目录一.详解编译与链接1.前言2.翻译环境3.剖析编译过程4.运行环境二.预处理详解1.预定义符号2.剖析#define(1).定义标识符(2).定义宏(3).替换规则(4).#和##(5).宏与函数的对比(6).#undef3.条件编译4.文件包含(1).头文件包含的方式(2).嵌套文件包含一.详解编译与链接 1.前言 在…...

【Docker知识】将环境变量传递到容器
一、说明 程序通常通过与软件捆绑在一起的配置来控制操作,环境变量允许用户在运行时设置它们。但是,在 Docker 容器中运行进程会使事情变得复杂,那么如何将环境变量传递给容器呢?下面介绍若干个传递办法。 二、环境变量有何用途 环…...

Allegro如何更改铜皮显示密度操作指导
Allegro如何更改铜皮显示密度操作指导 用Allegro做PCB设计的时候,铜皮正常显示模式如下图 铜皮的密度是基本填充满的,Allegro支持更改铜皮的显示密度 如下图 如何更改密度,具体操作如下 点击setup...
ThinkPHP5酒店预订管理系统
有需要请私信或看评论链接哦 可远程调试 ThinkPHP5酒店预订管理系统一 介绍 此酒店预订管理系统基于ThinkPHP5框架开发,数据库mysql,采用了ueditor富文本编辑器。系统角色分为用户,员工和管理员。用户可注册登录并预订酒店和评论等ÿ…...

【MySQL】MyCat分库分表分片规则配置详解与实战(MySQL专栏启动)
📫作者简介:小明java问道之路,2022年度博客之星全国TOP3,专注于后端、中间件、计算机底层、架构设计演进与稳定性建工设优化。文章内容兼具广度深度、大厂技术方案,对待技术喜欢推理加验证,就职于知名金融公…...

OpenWrt路由器设置域名动态解析手把手教程
文章目录0、前言1、准备工作2、详细步骤2.1、OpenWrt路由器软件包安装2.2、防火墙放行入站数据(修改为“接受”并保存应用)2.3、域名解析服务商对域名的解析设置2.4、路由器中动态域名插件的设置0、前言 因为一直用着内网穿透(zerotier或者是…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...
