动手学深度学习(Pytorch版)代码实践-深度学习基础-01基础函数的使用
01基础函数的使用
主要内容
- 张量操作:创建和操作张量,包括重塑、填充、逐元素操作等。
- 数据处理:使用pandas加载和处理数据,包括处理缺失值和进行one-hot编码。
- 线性代数:包括矩阵运算、求和、均值、点积和各种范数计算。
- 自动求导:使用
PyTorch的自动求导功能计算梯度,并演示梯度清除和分离计算图的操作。
import torch
import pandas as pd
import os# 创建和操作张量
# 张量表示一个数值组成的数组,这个数组可能有多个维度
x = torch.arange(12) # 创建一个包含从0到11的向量
print("x:", x) # 打印张量xprint("x的形状:", x.shape) # 打印张量的形状print("x中的元素总数:", x.numel()) # 打印张量中元素的总数# 改变一个张量的形状而不改变元素数量和元素值,采用reshape
X = x.reshape(3, 4) # 将x重塑为一个3行4列的矩阵
print("重塑后的X:", X) # 打印重塑后的X# 创建全0,全1张量
print("全零张量:", torch.zeros((2, 3, 4))) # 创建一个形状为(2,3,4)的全0张量
print("全一张量:", torch.ones((2, 3, 4))) # 创建一个形状为(2,3,4)的全1张量# 使用包含数值的Python列表创建张量
t = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]]) # 创建张量t
print("从列表创建的张量:", t) # 打印张量t
print("张量t的形状:", t.shape) # 打印张量t的形状# 张量操作
X = torch.arange(12, dtype=torch.float32).reshape((3, 4)) # 创建并重塑张量X
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]]) # 创建张量YZ = torch.zeros_like(X) # 创建一个形状和X相同的全零张量
Z[:] = X + Y # 计算X和Y的逐元素加法
print("Z (X + Y):", Z) # 打印Z
print("Z的转置:", Z.T) # 打印Z的转置# 使用pandas创建和处理数据集
# 创建一个人工数据集,并存储在CSV(逗号分隔值)文件中
os.makedirs(os.path.join('..', 'data'), exist_ok=True) # 创建数据目录
data_file = os.path.join('..', 'data', 'house_tiny.csv') # 定义文件路径
with open(data_file, 'w') as f:f.write('NumRooms,Alley,Price\n') # 列名f.write('NA,Pave,127500\n') # 每行表示一个数据样本f.write('2,NA,106000\n')f.write('4,NA,178100\n')f.write('NA,NA,140000\n')data = pd.read_csv(data_file) # 读取CSV文件
print("从CSV加载的数据:", data) # 打印加载的数据inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2] # 分离输入和输出
inputs['NumRooms'] = inputs['NumRooms'].fillna(inputs['NumRooms'].mean()) # 用均值填充缺失值
print("处理后的输入数据:", inputs) # 打印处理后的输入数据inputs = pd.get_dummies(inputs, dummy_na=True).astype('float') # 转换类别变量并将其转换为浮点型
print("独热编码后的输入数据:", inputs) # 打印独热编码后的输入数据X = torch.tensor(inputs.values) # 将输入数据转换为张量
Y = torch.tensor(outputs.values) # 将输出数据转换为张量
print("输入数据的张量X:", X) # 打印输入数据的张量X
print("输出数据的张量Y:", Y) # 打印输出数据的张量Y# 线性代数操作
A = torch.arange(20, dtype=torch.float32).reshape(5, 4) # 创建并重塑张量A
B = A.clone() # 通过分配新内存,将A的副本分配给B
print("矩阵A:", A) # 打印矩阵A
print("矩阵A + B:", A + B) # 矩阵加法
print("矩阵A * B:", A * B) # 矩阵逐元素乘法a = 2
X = torch.arange(24).reshape(2, 3, 4) # 创建并重塑张量X
print("张量X:", X) # 打印张量X
print("a + X:", a + X) # 标量和张量相加
print("a * X的形状:", (a * X).shape) # 打印标量和张量相乘后的形状# 求和与均值
A_sum_axis0 = A.sum(axis=0) # 沿着第0维度求和
print("沿第0维度求和:", A_sum_axis0, "形状:", A_sum_axis0.shape) # 打印求和结果及其形状print("A中的元素总数:", A.numel()) # 打印A中的元素总数
print("A的均值:", A.mean()) # 打印A的均值
print("A的和除以元素总数:", A.sum() / A.numel()) # 打印A的和除以元素总数sum_A = A.sum(axis=1, keepdims=True) # 沿第1维度求和,并保持维度
print("沿第1维度求均值,保持维度:", A.mean(axis=1, keepdim=True)) # 打印沿第1维度的均值,并保持维度
print("沿第1维度求和,保持维度:", sum_A) # 打印沿第1维度的求和,并保持维度print("A的归一化 (A / sum_A):", A / sum_A) # 打印归一化的Aprint("沿第0维度的累积和:", A.cumsum(axis=0)) # 打印沿第0维度的累积和# 点积
x = torch.arange(4, dtype=torch.float32) # 创建张量x
y = torch.ones(4, dtype=torch.float32) # 创建全1张量y
print("x和y的点积:", torch.dot(x, y)) # 打印x和y的点积
print("逐元素乘积的和:", torch.sum(x * y)) # 打印逐元素乘积的和print("矩阵A和向量x的乘积:", torch.mv(A, x)) # 打印矩阵和向量的乘积# 矩阵乘法
B = torch.ones(4, 3) # 创建全1矩阵B
print("矩阵A:", A) # 打印矩阵A
print("矩阵B:", B) # 打印矩阵B
print("矩阵A和B的矩阵乘法:", torch.mm(A, B)) # 打印矩阵A和B的矩阵乘法# 各种范数
u = torch.tensor([3.0, -4.0]) # 创建张量u
print("u的L2范数:", torch.norm(u)) # 打印u的L2范数
print("u的L1范数:", torch.abs(u).sum()) # 打印u的L1范数
print("一个全1矩阵(4x9)的弗罗贝尼乌斯范数:", torch.norm(torch.ones((4, 9)))) # 打印全1矩阵的弗罗贝尼乌斯范数print("张量元素的和:", sum(torch.arange(20, dtype=torch.float32))) # 打印张量元素的和A = torch.arange(40, dtype=torch.float32).reshape(2, 5, 4) # 创建并重塑张量A
print("3D张量A:", A) # 打印3D张量A
print("沿轴[1,2]求和:", A.sum(axis=[1, 2])) # 打印沿轴[1,2]求和结果
print("沿轴[1,2]求和,保持维度:", A.sum(axis=[1, 2], keepdims=True)) # 打印沿轴[1,2]求和结果,并保持维度A = torch.ones(2, 5, 4) # 创建全1张量A
print("3D张量A,全为1:", A) # 打印全1张量A
print("沿轴[0,1]求和,保持维度:", A.sum(axis=[0, 1], keepdim=True)) # 打印沿轴[0,1]求和结果,并保持维度# 自动求导
x = torch.arange(4.0) # 创建张量x
print("张量x:", x) # 打印张量xx.requires_grad_(True) # 开启自动求导
print("x的梯度 (初始为None):", x.grad) # 打印x的梯度 (初始为None)y = 2 * torch.dot(x, x) # 2 * (x · x) 求导为 4x
print("y = 2 * (x · x):", y) # 打印yy.backward() # 计算导数
print("backward之后x的梯度:", x.grad) # 打印x的梯度
print("x的梯度是否等于4 * x:", x.grad == 4 * x) # 打印x的梯度是否等于4 * x# 清除梯度
x.grad.zero_() # 清除x的梯度
y = x.sum()
y.backward()
print("求和y并backward之后的x梯度:", x.grad) # 打印求和y并backward之后的x梯度# 对非标量调用backward需要传入一个gradient参数
x.grad.zero_() # 清除x的梯度
y = x * x
y.sum().backward() # 等价于 y.backward(torch.ones(len(x)))
print("平方并求和y之后的x梯度:", x.grad) # 打印平方并求和y之后的x梯度# 分离计算图
x.grad.zero_() # 清除x的梯度
y = x * x
u = y.detach() # 从计算图中分离y
print("张量y:", y) # 打印张量y
print("从y分离的张量u:", u) # 打印从y分离的张量uz = u * x
z.sum().backward()
print("分离u乘以x的梯度:", x.grad == u) # 打印分离u乘以x的梯度x.grad.zero_() # 清除x的梯度
y.sum().backward()
print("再次求和y之后的x梯度:", x.grad == 2 * x) # 打印再次求和y之后的x梯度
相关文章:
代码实践-深度学习基础-01基础函数的使用)
动手学深度学习(Pytorch版)代码实践-深度学习基础-01基础函数的使用
01基础函数的使用 主要内容 张量操作:创建和操作张量,包括重塑、填充、逐元素操作等。数据处理:使用pandas加载和处理数据,包括处理缺失值和进行one-hot编码。线性代数:包括矩阵运算、求和、均值、点积和各种范数计算…...

vm-bhyve:bhyve虚拟机的管理系统@FreeBSD
先说情况,当前创建虚拟机后网络没有调通....不明白是最近自己点背,还是确实有难度... 缘起: 前段时间学习bhyve虚拟机,发现bvm这个虚拟机管理系统,但是实践下来发现网络方面好像有问题,至少我花了两天时间…...
【Java】刚刚!突然!紧急通知!垃圾回收!
【Java】刚刚!突然!紧急通知!垃圾回收! 文章目录 【Java】刚刚!突然!紧急通知!垃圾回收!从C语言的内存管理引入:手动回收Java的垃圾回收机制引用计数器循环引用问题 可达…...
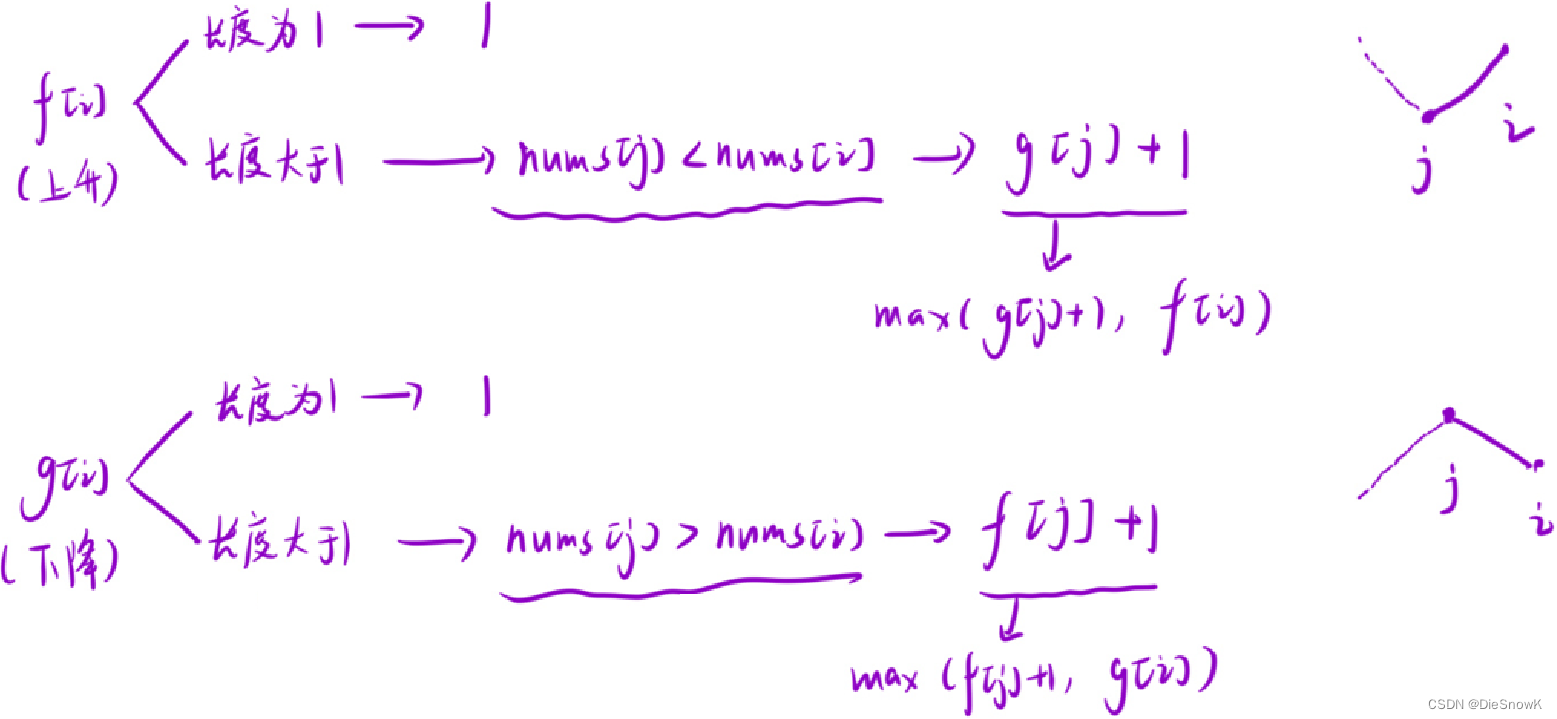
[Algorithm][动态规划][子序列问题][最长递增子序列][摆动序列]详细讲解
目录 0.子序列 vs 子数组1.最长递增子序列1.题目链接2.算法原理详解3.代码实现 2.摆动序列1.题目链接2.题目链接3.代码实现 0.子序列 vs 子数组 子序列: 相对顺序是跟源字符串/数组是一致的但是元素和元素之间,在源字符串/数组中可以是不连续的一般时间…...

【稳定检索】2024年心理学与现代化教育、媒体国际会议(PMEM 2024)
2024年心理学与现代化教育、媒体国际会议 2024 International Conference on Psychology and Modern Education and Media 【1】会议简介 2024年心理学与现代化教育、媒体国际会议即将召开,这是一场汇聚全球心理学、教育及媒体领域精英的学术盛宴。 本次会议将深入探…...
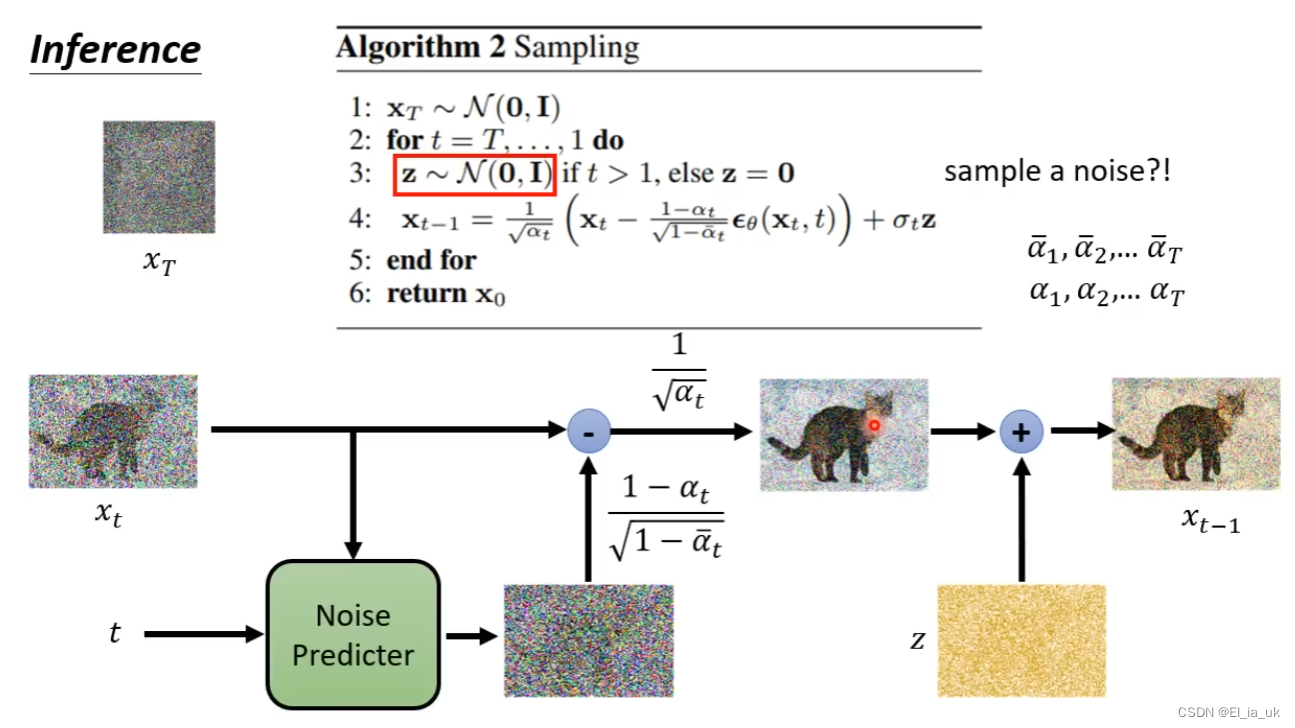
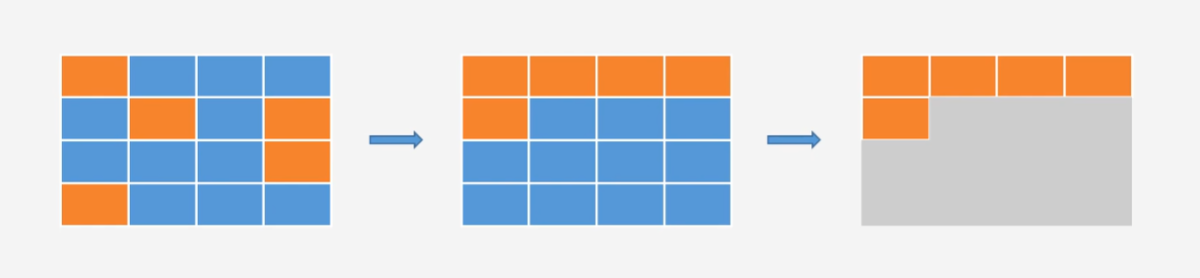
深入了解diffusion model
diffusion model是如何运作的 会输入当时noise的严重程度,根据我们的输入来确定在第几个step,并做出不同的回应。 Denoise模组内部实际做的事情 产生一张图片和产生noise难度是不一样的,若denoise 模块产生一只带噪声的猫说明这个模块已经会…...
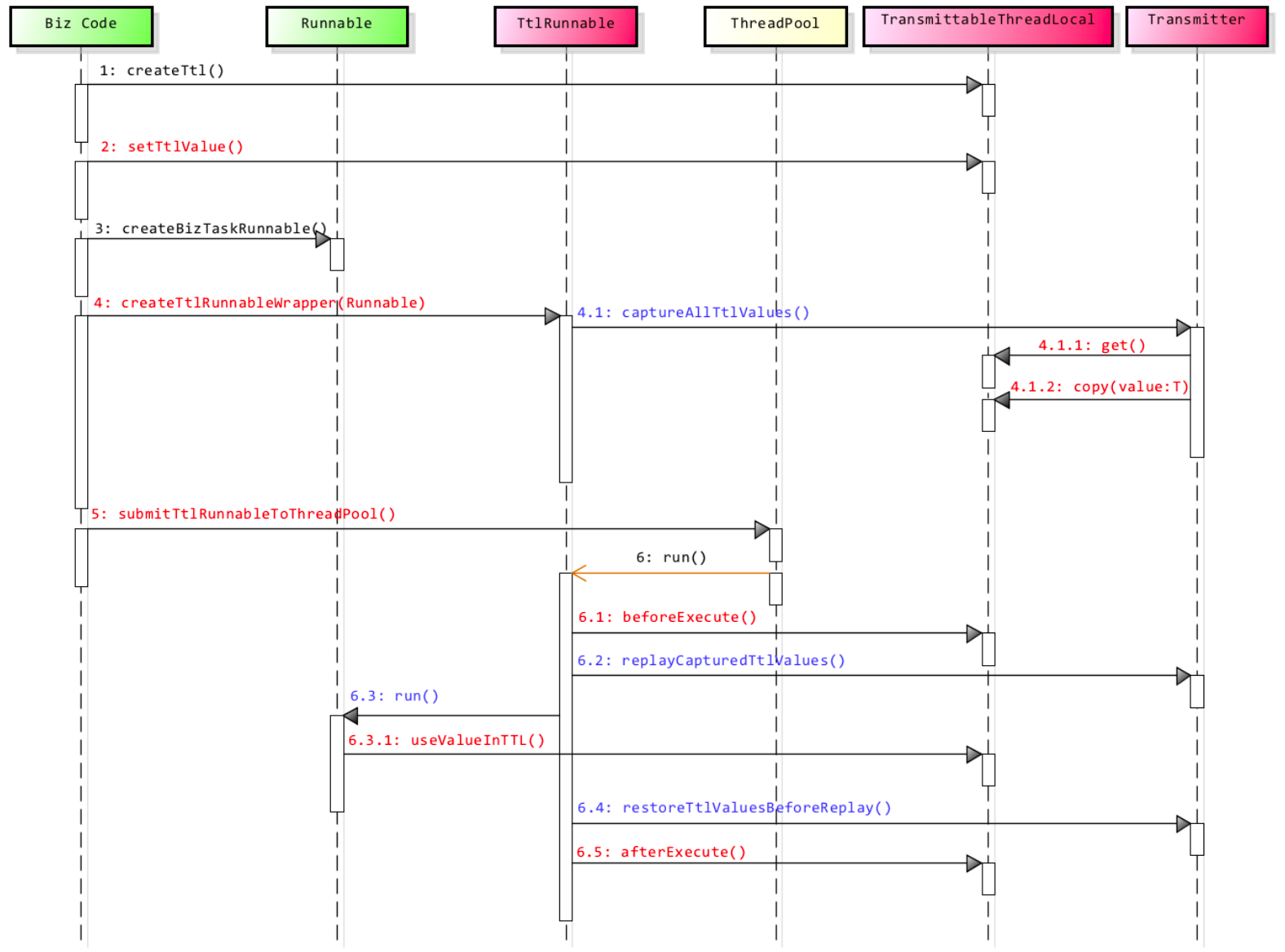
TransmittableThreadLocal原理
1、原理 TransmittableThreadLocal(简称TTL)是阿里巴巴开源的一个Java库,用于解决线程池中线程本地变量传递的问题。其底层原理主要是基于Java的ThreadLocal机制并对其进行扩展,以支持在父子线程间以及线程池中任务切换时&#x…...

华为昇腾310B初体验,OrangePi AIpro开发板使用测评
0、写在前面 很高兴收到官方的OrangePi AIpro开发板测试邀请,在过去的几年中,我在自己的博客写了一系列有关搭载嵌入式Linux系统的SBC(单板计算机)的博文,包括树莓派4系列、2K1000龙芯教育派、Radxa Rock5B、BeagleBo…...

GPTQ 量化大模型
GPTQ 量化大模型 GPTQ 算法 GPTQ 算法由 Frantar 等人 (2023) 提出,它从 OBQ 方法中汲取灵感,但进行了重大改进,可以将其扩展到(非常)大型的语言模型。 步骤 1:任意顺序量化 OBQ 方法选择权重按特定顺序…...

【GD32】05 - PWM 脉冲宽度调制
PWM PWM (Pulse Width Modulation) 是一种模拟信号电平的方法,它通过使用数字信号(通常是方波)来近似地表示模拟信号。在PWM中,信号的占空比(即高电平时间占整个周期的比例)被用来控制平均输出电压或电流。…...

JVM思维导图
帮助我们快速整理和总结JVM相关知识,有结构化认识和整体的思维模型 JVM相关详细知识和面试题...

Ollama+OpenWebUI+Phi3本地大模型入门
文章目录 Ollama+OpenWebUI+Phi3本地大模型入门一、基础环境二、Ollama三、OpenWebUI + Phi3Ollama+OpenWebUI+Phi3本地大模型入门 完全不懂大模型的请绕道,相信我李一舟的课程比较适合 Ollama提供大模型运行环境,OpenWebUI提供UI,Phi3就是那个大模型。 当然,Ollama支持超级…...
实战15:bert 命名实体识别、地址解析、人名电话地址抽取系统-完整代码数据
直接看项目视频演示: bert 命名实体识别、关系抽取、人物抽取、地址解析、人名电话地址提取系统-完整代码数据_哔哩哔哩_bilibili 项目演示: 代码: import re from transformers import BertTokenizer, BertForTokenClassification, pipeline import os import torch im…...

js 表格添加|删除一行交互
一、需求 二、实现 <div style"margin-bottom: 55px"><form action"" method"post" enctype"multipart/form-data" id"reportForm" name"sjf" style"margin-left: 25px;margin-bottom: 50px;&quo…...

如何选择合适的服务器硬件和配置?
业务需求 了解您的业务需求和负载。这将帮助您确定需要哪种类型的服务器(如文件服务器、数据库服务器、Web服务器等)以及所需的处理能力、内存、存储和网络性能。...
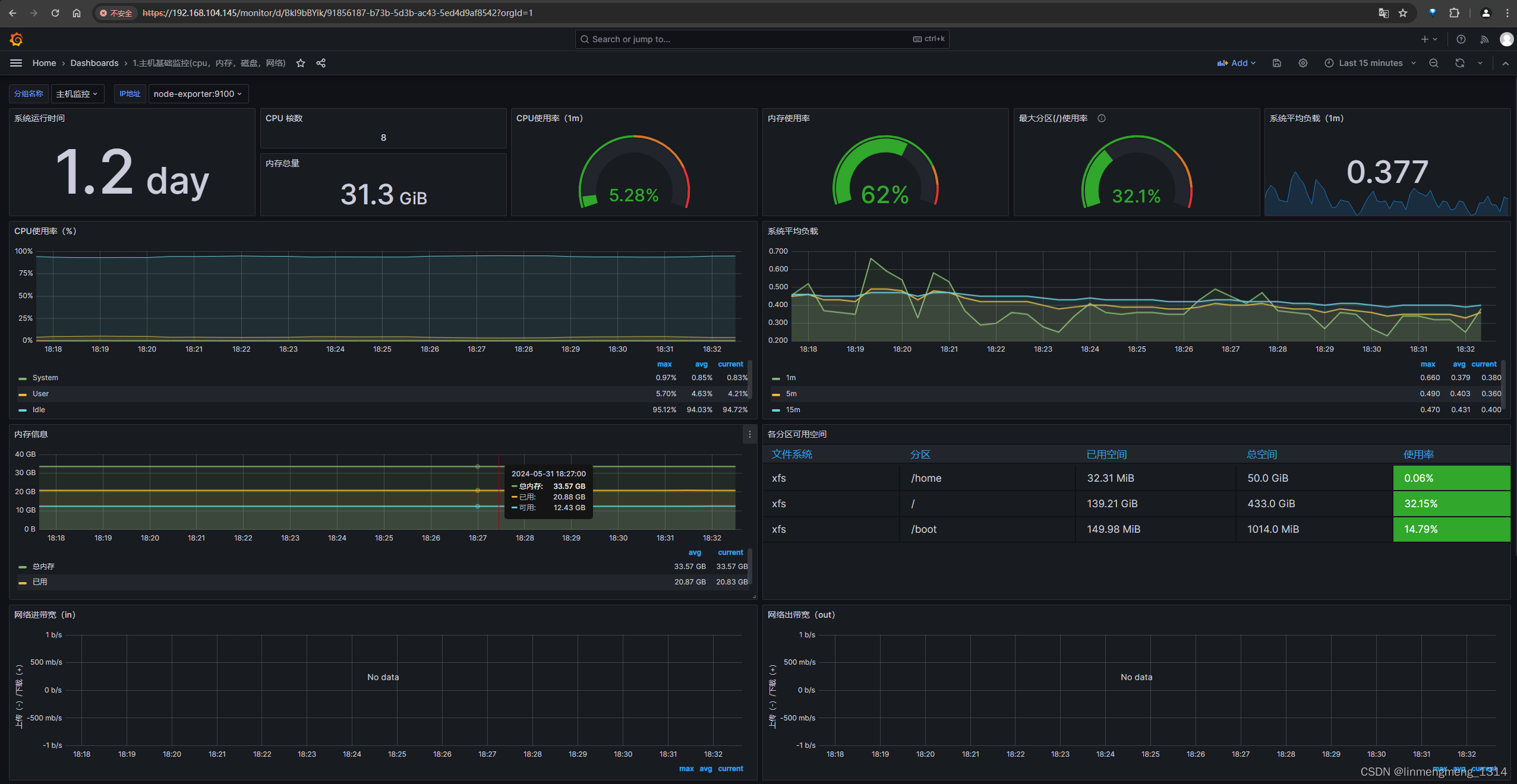
Prometheus + Grafana + Alertmanager 系统监控
PrometheusGrafana 系统监控 1. 简介1.1 Prometheus 普罗 米修斯1.2 Grafana 2. 快速试用2.1 Prometheus 普罗 米修斯2.2 Prometheus 配置文件2.3 Grafana 2. 使用 Docker-Compose脚本部署监控服务3. Grafana 配置3.1 配置数据源 Prometheus3.2 使用模板ID 配置监控模板3.3 使用…...

5.23R语言-参数假设检验
理论 方差分析(ANOVA, Analysis of Variance)是统计学中用来比较多个样本均值之间差异的一种方法。它通过将总变异分解为不同来源的变异来检测因子对响应变量的影响。方差分析广泛应用于实验设计、质量控制、医学研究等领域。 方差分析的基本模型 方差…...

rnn 和lstm源码学习笔记
目录 rnn学习笔记 lstm学习笔记 rnn学习笔记 import torchdef rnn(inputs, state, params):# inputs的形状: (时间步数量, 批次大小, 词表大小)W_xh, W_hh, b_h, W_hq, b_q paramsH stateoutputs []# 遍历每个时间步for X in inputs:# 计算隐藏状态 HH torch.tanh(torch.…...

解析Java中1000个常用类:CharSequence类,你学会了吗?
在 Java 编程中,字符串操作是最常见的任务之一。为了提供一种灵活且统一的方式来处理不同类型的字符序列,Java 引入了 CharSequence 接口。 通过实现 CharSequence 接口,各种字符序列类可以提供一致的 API,增强了代码的灵活性和可扩展性。 本文将深入探讨 CharSequence 接…...

微服务远程调用之拦截器实战
微服务远程调用之拦截器实战 前言: 在我们开发过程中,很可能是项目是从0到1开发,或者在原有基础上做二次开发,这次是根据已有代码做二次开发,需要在我们微服务一【这里方便举例,我们后面叫模版微服务】调用…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
