【强化学习】马尔可夫决策过程MDP
1.马尔可夫决策过程MDP
1.1 MDP五元组
MDP=<S,A,P,R,γ>MDP=<\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\mathcal{\gamma}>MDP=<S,A,P,R,γ>,其中:
- S\mathcal{S}S:状态空间
- A\mathcal{A}A:动作空间
- P\mathcal{P}P:P(s′∣s,a)\mathcal{P(s'|s,a)}P(s′∣s,a)为状态转移函数,表示采取动作aaa从状态sss转移到状态s′s's′的概率
- R\mathcal{R}R:奖励函数R(s,a)\mathcal{R(s,a)}R(s,a),表示在状态sss下采取动作aaa后的奖励。
- γ\mathcal{\gamma}γ:折扣因子γ∈[0,1)\gamma \in [0,1)γ∈[0,1),取值越大越注重长期积累的奖励。
- MDP与MRP的区分
MDP与马尔可夫奖励过程MRP=<S,P,r,γ>MRP=<\mathcal{S},\mathcal{P},\mathcal{r},\mathcal{\gamma}>MRP=<S,P,r,γ>的区别在于状态转移和奖励函数不依赖于动作aaa。举例:船在海上自由飘荡是一个MRP,船由水手掌舵在海上航行是一个MDP。
1.2 Agent与MDP环境的交互
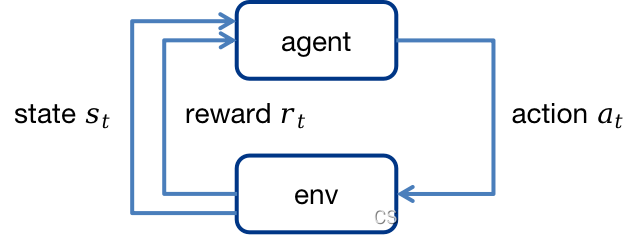
Agent通过rtr_trt学习策略,agent通过学习到的策略针对当前环境状态sts_tst采取相应动作ata_tat,该动作与环境交互后,环境中的状态将转移到新的状态st+1s_{t+1}st+1,同时获得奖励rt+1r_{t+1}rt+1。Agent的目标是最大化累积奖励的期望。
1.2.1 策略policy
策略用π\piπ表示,策略是一个函数,是agent学习的目标。策略会输出在状态sss下采取各个action的概率,即π(a∣s)=P(At=a∣St=s)\pi(a|s)=P(A_t=a|S_t=s)π(a∣s)=P(At=a∣St=s).
1.2.2 状态价值函数V(s)V(s)V(s)
Vπ(s)V^\pi(s)Vπ(s)表示从状态sss出发,采取策略π\piπ获得回报的期望,即
Vπ(s)=Eπ[Gt∣St=s]V^\pi(s) = E_\pi[G_t|S_t=s] Vπ(s)=Eπ[Gt∣St=s]
1.2.3 动作价值函数Q(a|s)
Qπ(a∣s)Q^\pi(a|s)Qπ(a∣s)表示MDP遵循策略π\piπ,在状态sss下采取动作aaa后得到回报的期望,即:
Qπ(a∣s)=Eπ[Gt∣St=s,At=a]Q^\pi(a|s)= E_\pi[G_t|S_t=s,A_t=a] Qπ(a∣s)=Eπ[Gt∣St=s,At=a]
- Vπ(s)V^\pi(s)Vπ(s) 与Qπ(a∣s)Q^\pi(a|s)Qπ(a∣s)的关系?
使用策略π\piπ,Vπ(s)V^\pi(s)Vπ(s) 为采取动作aaa的概率乘在状态sss下采取动作aaa的动作价值的累加和,即:
Vπ(s)=∑a∈Aπ(a∣s)Qπ(a∣s)V^\pi(s)=\sum_{a\in \mathcal{A}}\pi(a|s)Q^\pi(a|s)Vπ(s)=a∈A∑π(a∣s)Qπ(a∣s)
1.2.4 贝尔曼期望方程
Vπ(s)=Eπ[Gt∣St=s]=Eπ[Rt+γVπ(s′)∣St=s]=r(s,a)+γ\begin{aligned} V^\pi(s) &= E_\pi[G_t|S_t=s]\\ &=E_\pi[R_t+\gamma V^\pi(s')|S_t=s]\\ & =r(s,a)+\gamma \end{aligned} Vπ(s)=Eπ[Gt∣St=s]=Eπ[Rt+γVπ(s′)∣St=s]=r(s,a)+γ
Qπ(a∣s)=Eπ[Gt∣St=s,At=a]=Eπ[Rt+γQπ(s′∣s,a)∣St=s,At=a]\begin{aligned} Q^\pi(a|s) &= E_\pi[G_t|S_t=s,A_t=a]\\ &=E_\pi[R_t+\gamma Q^\pi(s'|s,a)|S_t=s,A_t=a] \end{aligned} Qπ(a∣s)=Eπ[Gt∣St=s,At=a]=Eπ[Rt+γQπ(s′∣s,a)∣St=s,At=a]
相关文章:

【强化学习】马尔可夫决策过程MDP
1.马尔可夫决策过程MDP 1.1 MDP五元组 MDP<S,A,P,R,γ>MDP<\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\mathcal{\gamma}>MDP<S,A,P,R,γ>,其中: S\mathcal{S}S:状态空间A\mathcal{A}A:动作空间P\mathc…...

刘润:五维思考,让你站得更高、看得更远
原标题:刘润:五维思考,让你站得更高、看得更远 前言:遇到问题时,有的人很快就能想明白,有的人需要很久才能想明白,还有的人始终都想不明白。 而且,那些很快就能想明白的人࿰…...
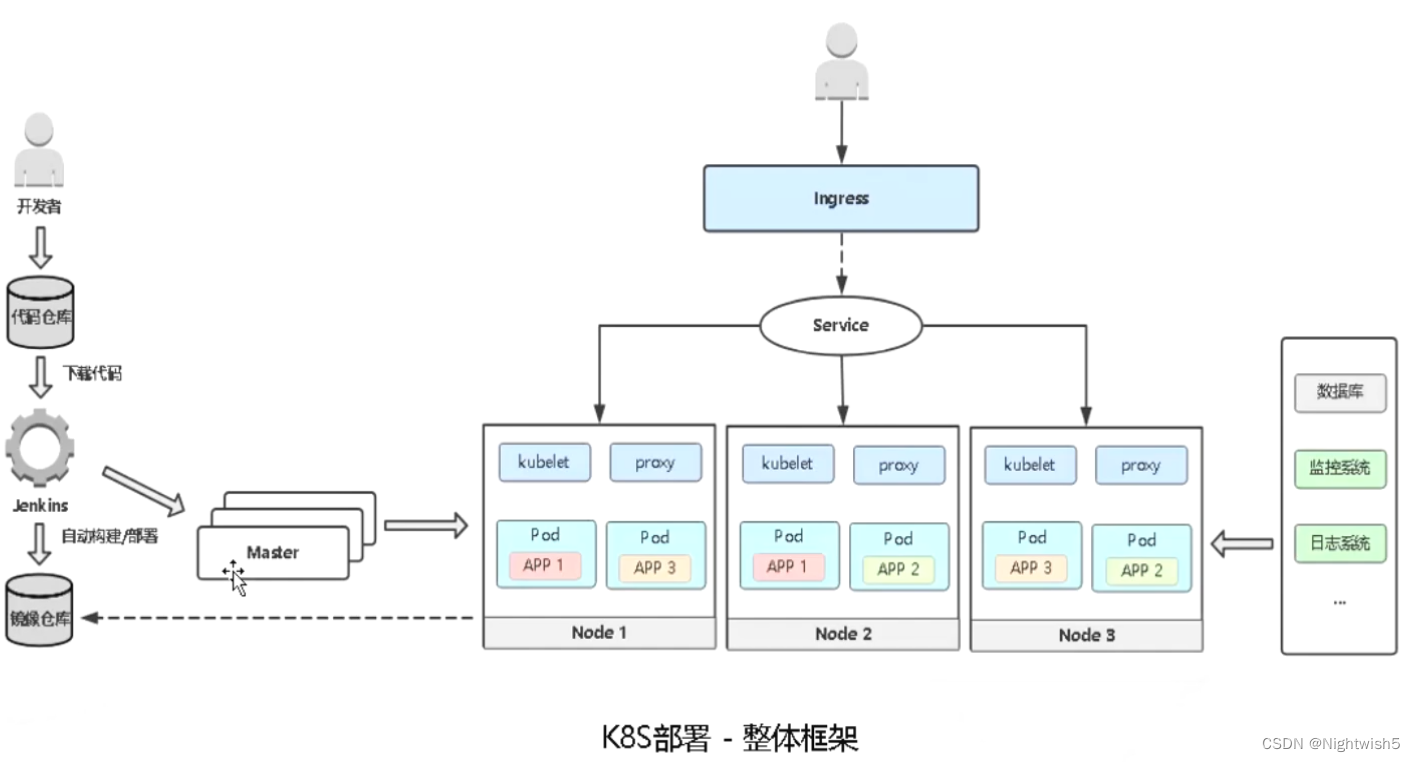
从运维角度看微服务 k8s部署微服务【偏理论】【AL】
从运维角度看微服务 & 部署微服务【偏理论】 1、微服务的特点 服务组件化: 每个服务独立开发、部署,有效避免一个服务的修改引起整个系统重新部署。 技术栈灵活: 约定通信方式,使得服务本身功能实现对技术要求不再那么敏感。…...
专题 | 防抖和节流
一 防抖:单位时间内,频繁触发事件,只执行最后一次 场景:搜索框搜索输入(利用定时器,每次触发先清掉以前的定时器,从新开始) 节流:单位时间内,频繁触发事件&…...

C++入门:重载运算符和重载函数
C 允许在同一作用域中的某个函数和运算符指定多个定义,分别称为函数重载和运算符重载。重载声明是指一个与之前已经在该作用域内声明过的函数或方法具有相同名称的声明,但是它们的参数列表和定义(实现)不相同。当您调用一个重载函…...

conda 新建虚拟环境 等等
1:conda create -n env_name package_name #创建名为env_name的新环境,并在该环境下安装名为package_name 的包,例如:conda create -n Arg python3.8 # 创建名字为Arg python为3.8版本的虚拟环境2: conda activate env…...
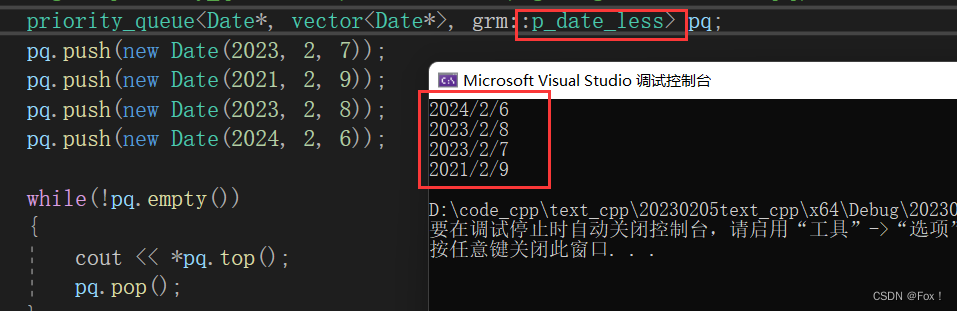
【C++:STL之栈和队列 | 模拟实现 | 优先级队列 】
目录 1. stack的介绍和使用 1.1 stack的介绍 1.2 stack的使用 2 栈的模拟实现 3 queue的介绍和使用 3.1 queue的介绍 3.2 queue的使用 4 queue的模拟实现 5 deque的介绍 5.1deque的原理介绍 5.2 deque的缺陷 5.3 为什么选择deque作为stack和queue的底层默认容器 6 p…...
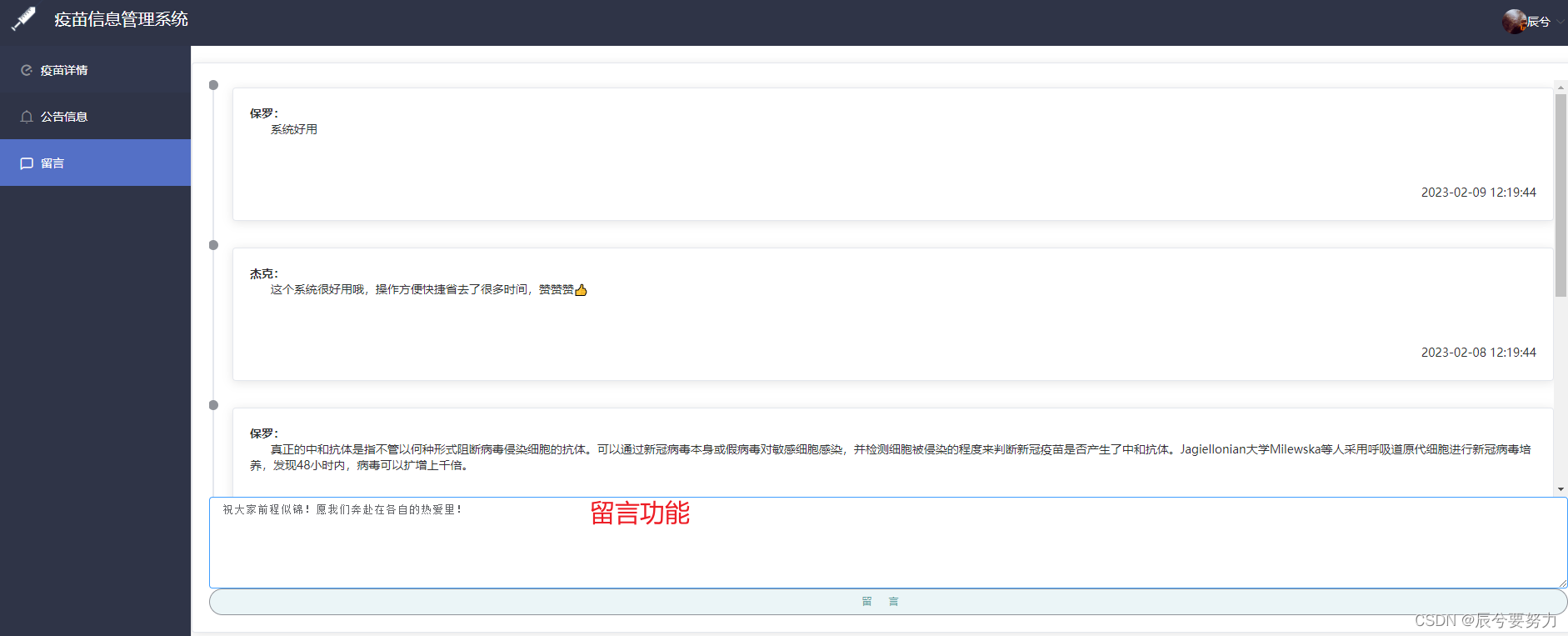
基于SpringBoot+Vue的疫苗预约管理系统(Java项目)
【辰兮要努力】:hello你好我是辰兮,很高兴你能来阅读,昵称是希望自己能不断精进,向着优秀程序员前行! 博客来源于项目以及编程中遇到的问题总结,偶尔会有读书分享,我会陆续更新Java前端、后台、…...
,真题含思路)
华为OD机试 - 计算网络信号(Python),真题含思路
计算网络信号 题目 网络信号经过传递会逐层衰减,且遇到阻隔物无法直接穿透,在此情况下需要计算某个位置的网络信号值。 注意:网络信号可以绕过阻隔物 array[m][n] 的二维数组代表网格地图,array[i][j] = 0 代表 i 行 j 列是空旷位置;array[i][j] = x ( x 为正整数)代表 i …...

【Spring】注解实现IOC操作,你理解了吗?
作者:狮子也疯狂 专栏:《spring开发》 坚持做好每一步,幸运之神自然会驾凌在你的身上 专栏推荐:写文章刚刚起步,各个专栏的知识点后续会补充完善,不断更新好文,希望大 家支持一下。 专栏名字El…...

微搭低代码从入门到精通01-总体介绍
在过去我们开发小程序,要学习各类知识。比如前端知识、后端知识、服务器知识及各种中间件及数据库的知识。 要想学会这些知识,既需要投入大量的学习时间,而且要经过相当的实践才可以掌握。 如果立志从事开发行业,投入精力去学习…...

类的继承
类的继承:一个类继承另一个类,自动拥有这个类的属性和方法,类似于包含与被包含的关系。被继承的类称为父类--子类则是继承父类的类。一个父类可以有多个子类;一个子类可以有多个父类(多继承)问题创建子类时…...

应用场景一:西门子PLC通过桥接器连接MQTT服务器
应用场景描述: 云平台、MES等数据采集、设备管理系统,需要通过MQTT的方式,上传和下发数据,MQTT服务器可以获取PLC的实时状态数据,也可以下发控制指令。桥接器提供4G、WIFI和有线三种连接方式。 网络拓扑:…...
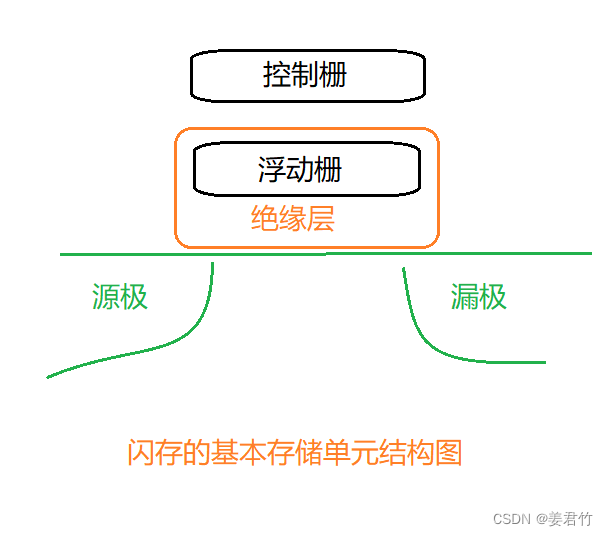
计算机组成原理(四)
1.理解存储器的分类方法;理解存储器的层次结构;熟悉存储器的几个技术指标(主要是存储容量、存取时间、存取周期、存储器带宽等); 存储器分类方法: 按与CPU的连接和功能分类: 主存储…...
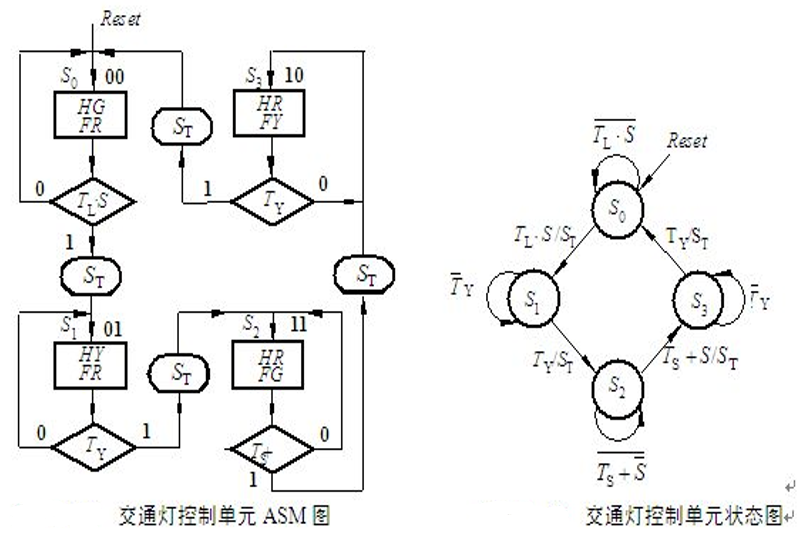
状态机设计举例
⭐本专栏针对FPGA进行入门学习,从数电中常见的逻辑代数讲起,结合Verilog HDL语言学习与仿真,主要对组合逻辑电路与时序逻辑电路进行分析与设计,对状态机FSM进行剖析与建模。 🔥文章和代码已归档至【Github仓库…...

Kubernetes1.25中Redis单机和集群部署实例二
1、概述我们知道在 Kubernetes 容器编排平台中, 我们可以非常方便的进行应用的扩容缩, 同时也能非常方便的进行业务的迭代,本章主要讲解在Kubernetes1.25搭建Redis单实例和Redis集群主从同步的环境流程步骤, 如果是高频访问重要的线上业务我们最好是部署在物理机器上…...
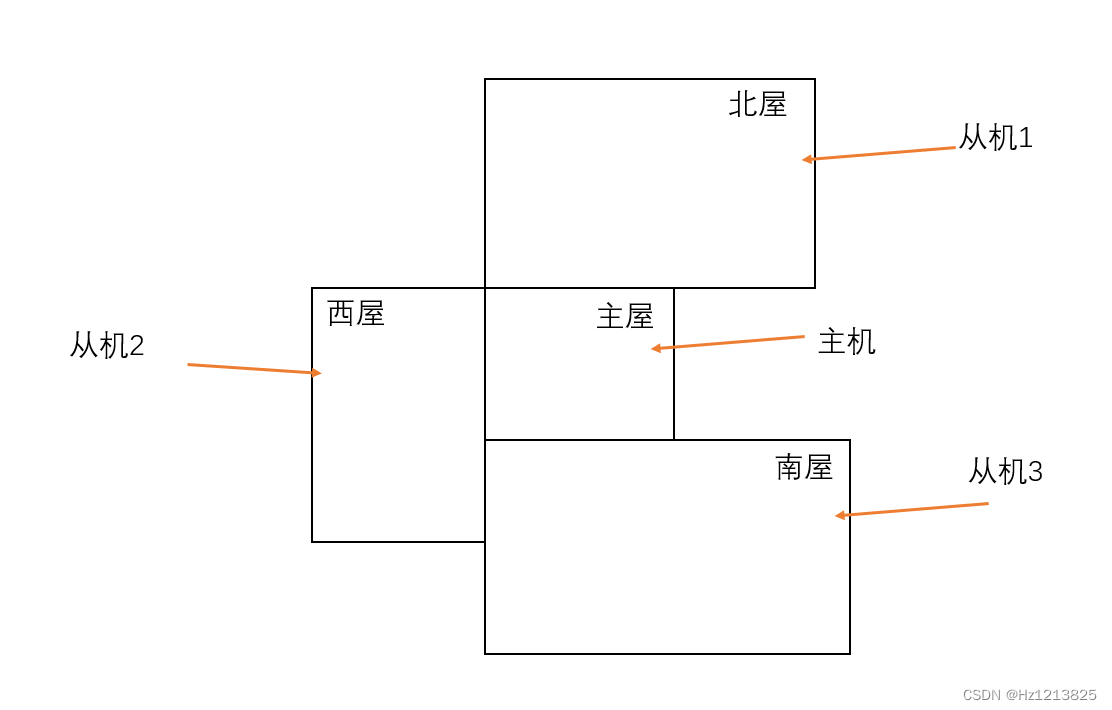
【STM32】【HAL库】遥控关灯0 概述
相关连接 【STM32】【HAL库】遥控关灯0 概述 【STM32】【HAL库】遥控关灯1主机 【STM32】【HAL库】遥控关灯2 分机 【STM32】【HAL库】遥控关灯3 遥控器 需求 家里有几个房间,开关距离床都挺远的 睡觉想要关灯的时候需要下床 因此设计了本次项目 需要满足以下要求: 可以控…...

C语言学习笔记(三): 选择结构程序设计
if语句 if(){} if (a1){printf("hehe");} //单独一个ifif(){}else{} int a 1, b 2;if (a b) {printf("haha"); //if else}else{printf("hehe");}if(){}else if(){} int a 1, b 2;if (a b) {printf("haha");}else if (a …...

图----无向图
1.定义 图的定义:图是由一组顶点和一组能够将两个顶点相连的边组成 边:edge 顶点:vertex 连通图:如果从任意一个顶点都存在一条路径到达另外一个任意顶点,我们称这幅图是连通图。 非连通图:由若干连通的…...
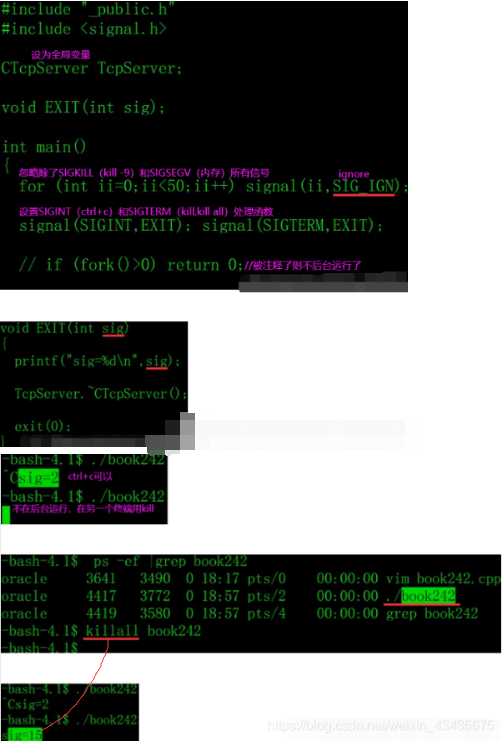
【C++1】函数重载,类和对象,引用,/string类,vector容器,类继承和多态,/socket,进程信号
文章目录1.函数重载:writetofile(),Ctrue和false,C0和非02.类和对象:vprintf构造函数:对成员变量初始化析构函数:一个类只有一个,不允许被重载3.引用:C中&取地址,C中…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
