《庆余年算法番外篇》:范闲通过最短路径算法在阻止黑骑截杀林相
剧情背景
在《庆余年 2》22集中,林相跟大宝交代完为人处世的人生哲理之后,就要跟大宝告别了
在《庆余年 2》23集中,林相在告老还乡的路上与婉儿和大宝告别后
范闲也在与婉儿的对话中知道黑骑调动是绝密,并把最近一次告老还乡梅执礼被马匪截杀与黑骑调动日期关联在一起,范闲知道了老皇帝要杀林相消息,所以范闲必须尽快找到一条最短路径在黑骑到之前去营救林相。这时候范闲在另外一个世界带来的记忆突然奔袭而来,马上想到用于地图导航GPS的Dijkstra算法,得找到路程最短的路径赶在黑骑到达前才能拯救林相,而在此之前他早就把庆国地形和路径都让人探究清楚了。知道黑骑所在位置到林相的位置大概需要75分钟。
现状输入描述
- 起点A:范闲目前所在的位置。
- 中点B:林相目前所在的位置。
- 节点集:A和B之间的多个节点路口CDEGF(例如路上的交叉点、村庄等)。
- 路程:连接这些节点的道路,每条道路有对应的行驶时间。
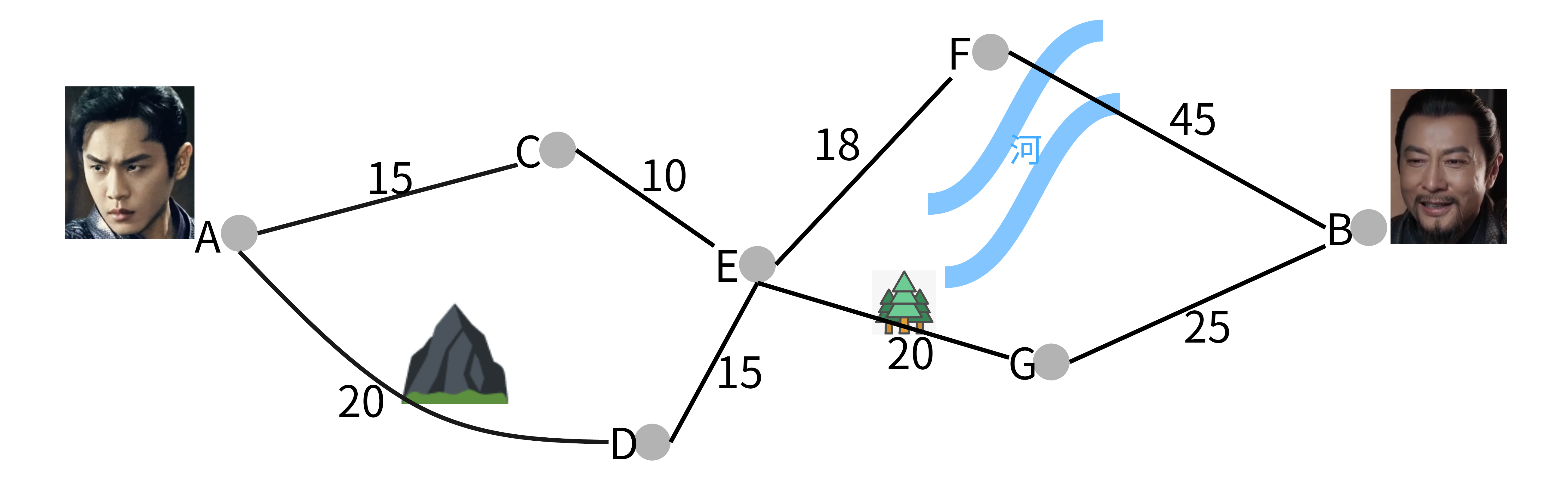
使用Dijkstra算法求解最短路径
实现原理
- Dijkstra 算法从指定的节点(源节点)出发,寻找它与图中所有其它节点之间的最短路径。
- Dijkstra 算法会记录当前已知的最短路径,并在寻找到更短的路径时更新。
- 一旦找到源节点与其他节点之间的最短路径,那个节点会被标记为“已访问”并添加到路径中。
- 重复寻找过程,直到图中所有节点都已经添加到路径中。这样,就可以得到从源节点出发访问所有其他节点的最短路径方案。
以下是详细的步骤和计算过程:
步骤 1: 初始化
- 起点A到所有其他节点的初始距离设为无穷大,除了起点本身,其距离为0。
- 使用优先队列初始化,从起点A开始。
距离:
A: 0
C: ∞
D: ∞
E: ∞
F: ∞
G: ∞
B: ∞优先队列:
[(0, 'A')]
步骤 2: 处理节点A
- 从A出发,可以到C和D,更新距离。
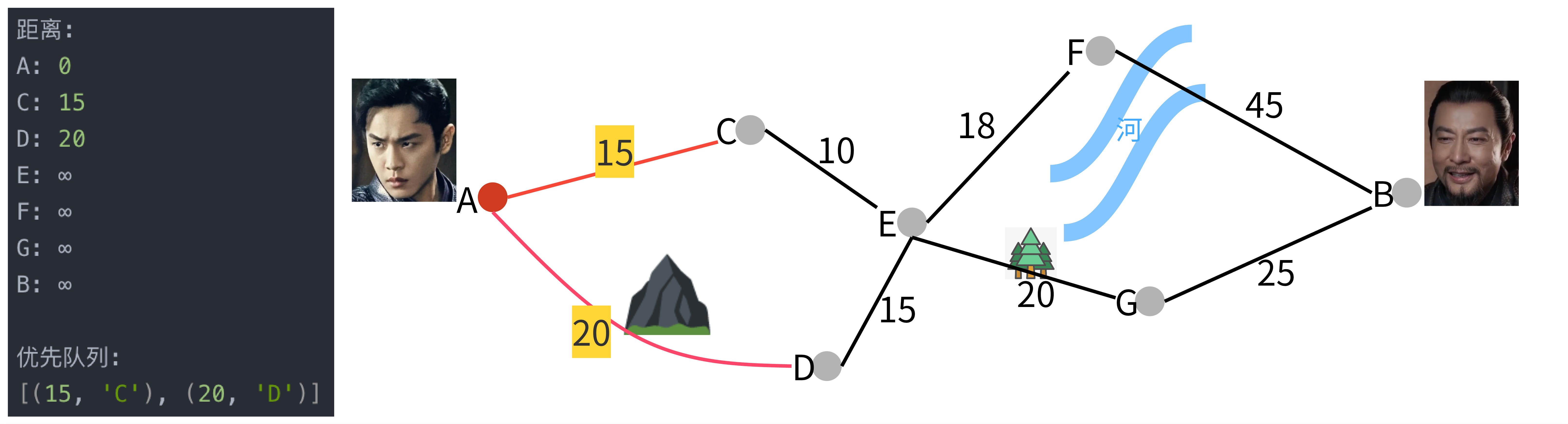
步骤 3: 处理节点C
- 从C出发,可以到E,更新距离。
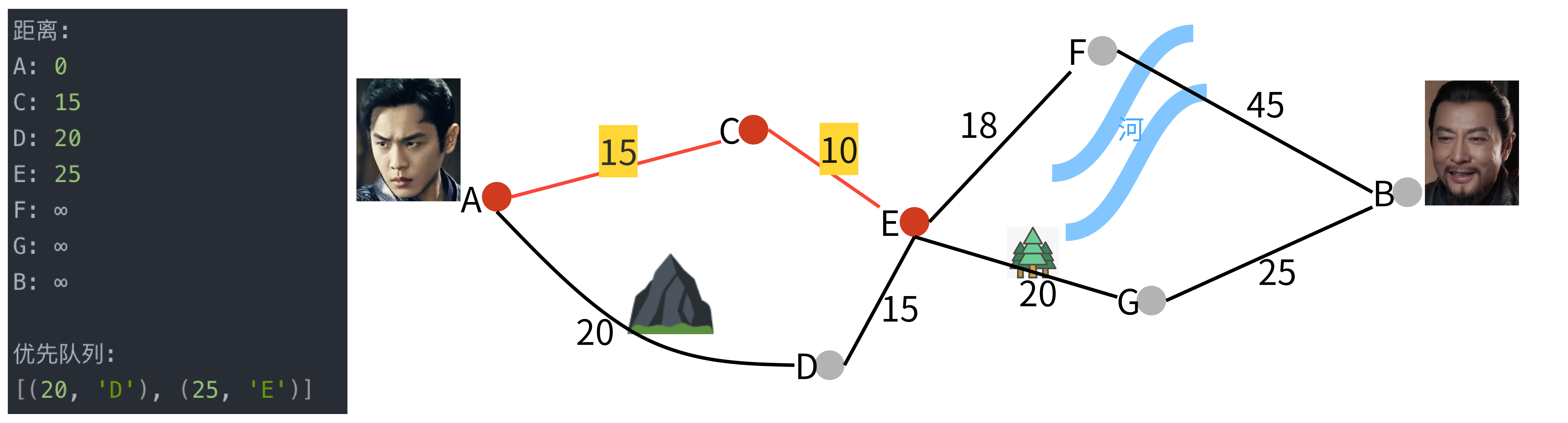
步骤 4: 处理节点D
- 从D出发,可以到E,但已有更短路径 C -> E,不更新。
距离:
A: 0
C: 15
D: 20
E: 25
F: ∞
G: ∞
B: ∞优先队列:
[(25, 'E')]
步骤 5: 处理节点E
- 从E出发,可以到F和G,更新距离。
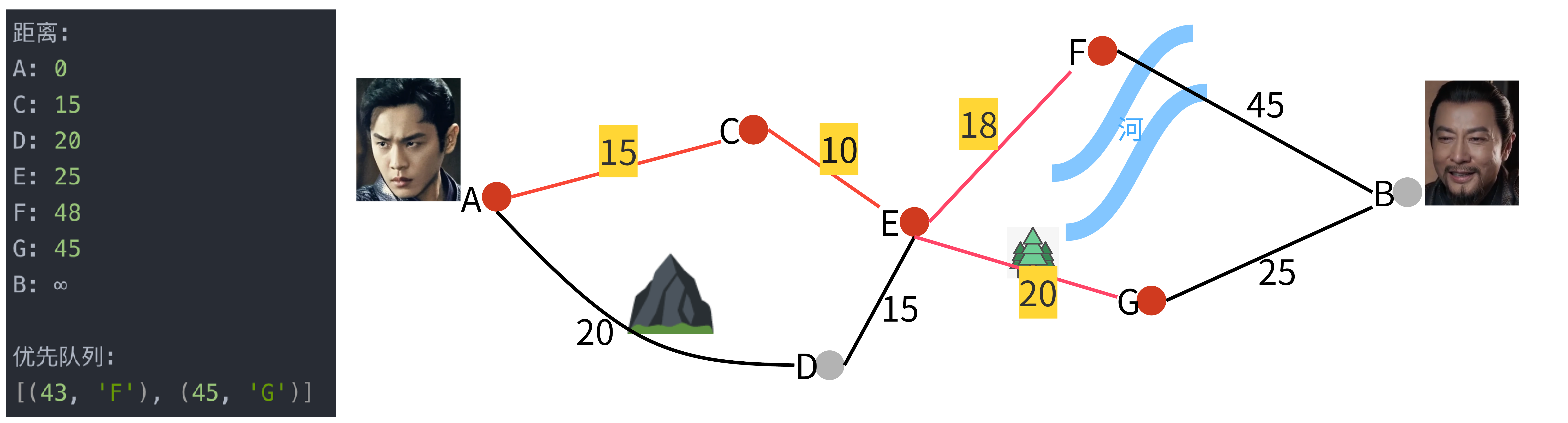
步骤 6: 处理节点F
- 从F出发,可以到B,更新距离。
距离:
A: 0
C: 15
D: 20
E: 25
F: 43
G: 45
B: 88优先队列:
[(45, 'G'), (88, 'B')]
步骤 7: 处理节点G
- 从G出发,可以到B,更新距离。
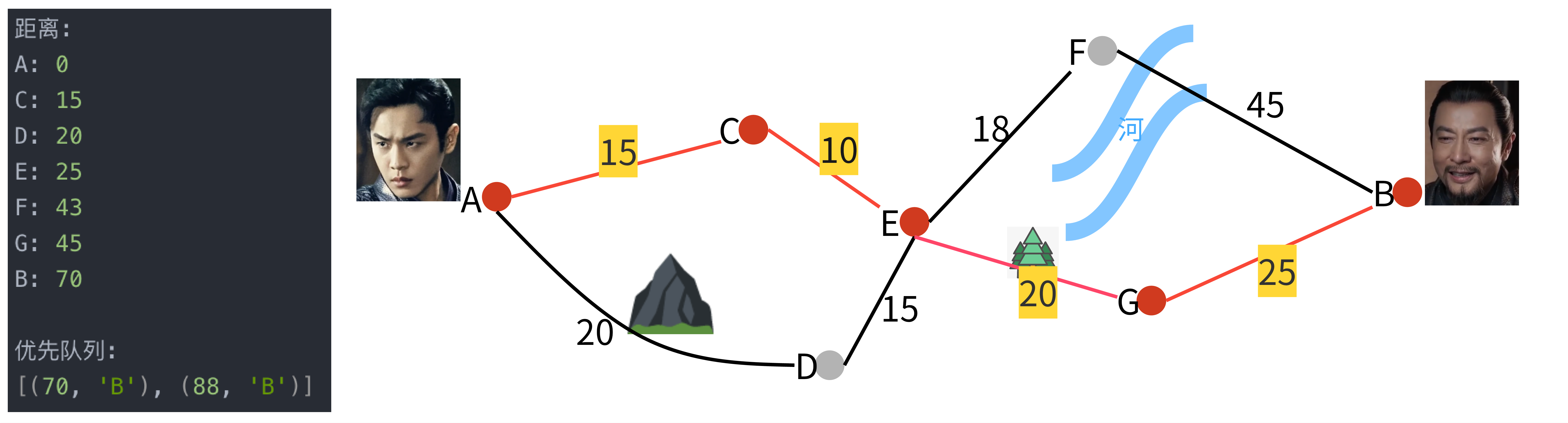
结果
通过Dijkstra算法计算,范闲从A到B的最短路径是A -> C -> E -> G -> B,总时间为:
- A -> C:15分钟
- C -> E:10分钟
- E -> G:20分钟
- G -> B:25分钟
- 总时间:15 + 10 + 20 + 25 = 70分钟 (黑骑到林相需要75分钟)
这时候选择A -> C -> E -> G -> B 因为没有导航刚刚手动计算已经花了两分钟了,情况紧急叫来王启年,马上赶路
王启年说范闲我们两个打不过黑骑,但是范闲说情况紧急没法给你找兵马,要去拼一把,跟打工人不给资源不给权利但是还要让你做出业绩一样、跟研究生不给钱不给署名还要写出论文一样

这里可以看出王启年作为一个优秀员工,肯定每年拿E,这表情比老板还急

从这里可以看出来,王启年业务能力也是一流,跑的比骑马快

按预期时间总算到了,开始正面刚黑骑

王启年虽然辛苦,但是范闲作为老板还是能抗事,马上承担责任,确保拿到结果,取得业绩有超强的领导力,是一个好老板

参考代码
import heapqdef dijkstra(graph, start):queue = [(0, start)]distances = {node: float('inf') for node in graph}distances[start] = 0while queue:current_distance, current_node = heapq.heappop(queue)if current_distance > distances[current_node]:continuefor neighbor, weight in graph[current_node].items():distance = current_distance + weightif distance < distances[neighbor]:distances[neighbor] = distanceheapq.heappush(queue, (distance, neighbor))return distances# 图的邻接表表示
graph = {'A': {'C': 15, 'D': 20},'C': {'A': 15, 'E': 10},'D': {'A': 20, 'E': 15},'E': {'C': 10, 'D': 15, 'F': 18, 'G': 20},'F': {'E': 18, 'B': 45},'G': {'E': 20, 'B': 25},'B': {'F': 45, 'G': 25}
}# 计算从起点A到各节点的最短路径
start = 'A'
distances = dijkstra(graph, start)
print(f"从{start}到各节点的最短路径: {distances}")
写到最后
希望文章能让大家放松的同时有知识进入到脑子里
这里作者祝大家:
- 高考\期末考的同学们:笔尖跃动光辉梦,心中理想定成真
- 毕业生们:才华扬帆乘风起,壮志凌云展未来
- 正在工作:不畏艰难勇向前,努力奋斗创佳绩
- 老板领导们:睿智领导拓新路,胸怀广阔业绩殊
相关文章:

《庆余年算法番外篇》:范闲通过最短路径算法在阻止黑骑截杀林相
剧情背景 在《庆余年 2》22集中,林相跟大宝交代完为人处世的人生哲理之后,就要跟大宝告别了 在《庆余年 2》23集中,林相在告老还乡的路上与婉儿和大宝告别后 范闲也在与婉儿的对话中知道黑骑调动是绝密,并把最近一次告老还乡梅…...

大一C语言课设 服装销售系统 代码实现与项目总结
问题分析 服装信息管理及销售管理系统。方便对库存服装的信息管理和添加新服装数据,同时兼具库存数量管理功能。 功能实现 1、建立服装信息库,包括:服装代码、型号、规格、面料、颜色、单价、数量; 2、建立销售信息库ÿ…...
从新手到专家:深入探索JVM垃圾回收--开端篇
引言: 在Java的世界里,垃圾回收(Garbage Collection, GC)机制扮演着至关重要的角色,它决定了Java应用的性能、稳定性和扩展性。本系列文章旨在深入探讨JVM中的垃圾回收技术,从基础的概念讲起,直…...
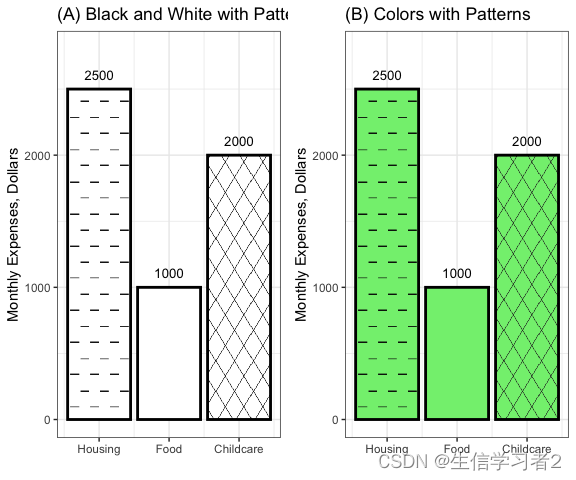
R可视化:另类的柱状图
介绍 方格状态的柱状图 加载R包 knitr::opts_chunk$set(echo TRUE, message FALSE, warning FALSE) library(patternplot) library(png) library(ggplot2) library(gridExtra)rm(list ls()) options(stringsAsFactors F)导入数据 data <- read.csv(system.file(&qu…...
Docker的数据管理(数据卷+数据卷容器)
文章目录 一、Docker的数据管理1、概述2、主要的技术(三种数据挂载方式)2.1、数据卷(Volumes)2.2、绑定挂载(Bind mounts)2.3、tmpfs挂载(Tmpfs mounts)2.4、之间的关系(…...
字符串-至多包含K种字符的子串中最长子串(mid)
一、题目描述 二、解题思路 借鉴以下题目思想,使用双指针,外层循环右侧指针移动,内存循环左侧指针移动 字符串-最长不含重复字符的子字符串(mid)-CSDN博客文章浏览阅读622次,点赞17次,收藏4次。java刷题:…...

Docker从安装开始精通
从虚拟机到容器 1.环境配置的难题 软件开发最大的麻烦事之一,就是环境配置。用户计算机的环境都不相同,你怎么知道自家的软件,能在那些机器跑起来? 用户必须保证两件事:操作系统的设置,各种库和组件的安装…...
)
MFC:初步理解序列化与反序列化(含代码实现)
序列化与反序列化是MFC将对象数据以二进制数据流的形式进行存储和读取的机制,读、写的效率很高。通过序列化与反序列化,可以将程序中对象在内存中数据保存到文件 (磁盘) 或者从文件 (磁盘) 中读取到内存以恢复对象数据,从而实现程序对数据的持…...

python程序控制结构
文章目录 一、python程序控制结构介绍二、顺序结构2.1、print()函数2.2、end参数2.3、input()函数 三、选择结构3.1选择结构的用途 四、循环结构4.1循环结构的构造4.1.1、循环结构的三个要素4.1.2、循环结构的一个要求4.1.3、循环结构的一个关系 4.2、循环语句4.2.1、while语句…...

【GD32】04 - Timer定时器
GD32中的定时器 GD32E230中有七个定时器,六种类型,其中通用的L4版本有两个,其他类型的各一个。 那我们就以通用L4这个类型来敲代码,其他流程是通用的。 通用L4 虽然每种类型的定时器都有自己的结构框图,但是其实大差…...

Golang | Leetcode Golang题解之第123题买卖股票的最佳时机III
题目: 题解: func maxProfit(prices []int) int {buy1, sell1 : -prices[0], 0buy2, sell2 : -prices[0], 0for i : 1; i < len(prices); i {buy1 max(buy1, -prices[i])sell1 max(sell1, buy1prices[i])buy2 max(buy2, sell1-prices[i])sell2 m…...
Leetcode2028. 找出缺失的观测数据
Every day a Leetcode 题目来源:2028. 找出缺失的观测数据 解法1:模拟 统计当前 m 个元素的总和 curSum sum(rolls),总共 mn 个元素和为 total (m n) * mean。 排除 2 种情况: total - curSum > 6 * n:n 个…...

如何在CentOS中合理划分磁盘空间以优化系统性能
目录 前言 理想的分区方案 为什么需要单独分区 安全性 性能 管理和维护 稳定性和可靠性 升级和兼容性 结论 前言 在进行CentOS系统的安装和配置时,合理划分磁盘空间是确保系统性能、安全性和易于管理的关键步骤。本文将探讨如何根据系统的硬件配置和预期用途…...
算法(十一)贪婪算法
文章目录 算法简介算法概念算法举例 经典问题 -背包问题 算法简介 算法概念 贪婪算法(Greedy)是一种在每一步都采取当前状态下最好的或者最优的选择,从而希望导致结果也是全局最好或者最优的算法。贪婪算法是当下局部的最优判断,…...
Rust之函数式语言特性:迭代器和闭包(一):概述
开发环境 Windows 11Rust 1.78.0 VS Code 1.89.1 项目工程 这次创建了新的工程minigrep. 函数式语言特性:迭代器和闭包 Rust的设计从许多现有语言和技术中获得了灵感,其中一个重要影响是函数式编程。函数式编程通常包括通过在参数中传递函数、从其他函数返回函数、…...

配置资源管理
一 Secret Secret 是用来保存密码、token、密钥等敏感数据的 k8s 资源,这类数据虽然也可以存放在 Pod 或者镜像中,但是放在 Secret 中是为了更方便的控制如何使用数据,并减少暴露的风险。 1 有三种类型: kubernetes.io/service…...
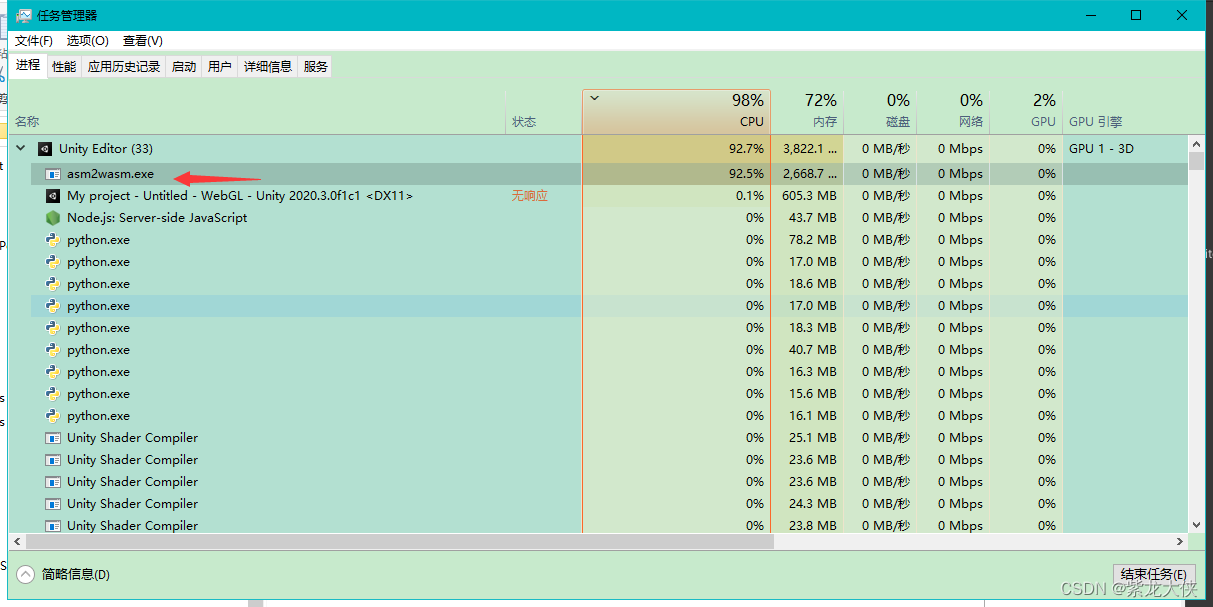
unity2020打包webGL时卡进程问题
我使用的2020.3.0f1c1,打包发布WEB版的时候会一直卡到asm2wasm.exe这个进程里,而且CPU占用率90%以上。 即使是打包一个新建项目的空场景也是同样的问题,我尝试过一直卡在这里会如何,结果还真打包成功了。只是打包一个空场景需要20…...

云原生架构相关技术_3.无服务器技术
1.技术特点 1.1面向特定领域的后端云服务(BaaS) 随着以Kubernetes为代表的云原生技术成为云计算的容器界面,Kubernetes成为云计算的新一代操作系统。面向特定领域的后端云服务(BaaS)则是这个操作系统上的服务API&…...
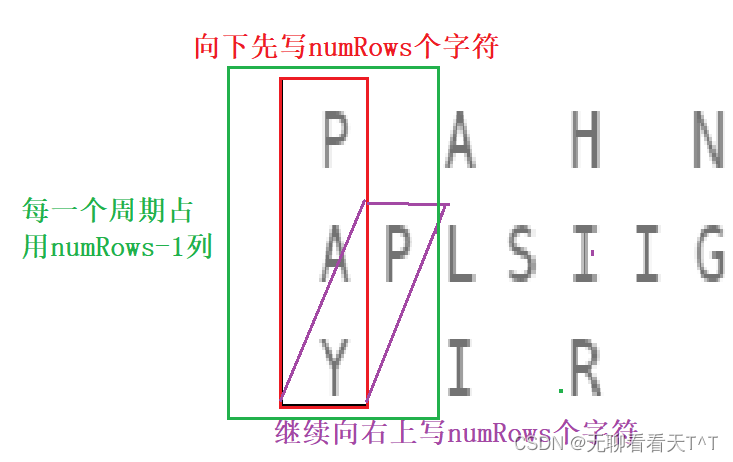
Leetcode:Z 字形变换
题目链接:6. Z 字形变换 - 力扣(LeetCode) 普通版本(二维矩阵的直接读写) 解决办法:直接依据题目要求新建并填写一个二维数组,最后再将该二维数组中的有效字符按从左到右、从上到下的顺序读取并…...

Python 3 判断文件是否存在
1 使用os.path模块 import osfile_path hello.txtif os.path.exists(file_path):print(f"文件 {file_path} 存在。") else:print(f"文件 {file_path} 不存在。") 2 使用pathlib模块 from pathlib import Pathfile_path Path(word.txt)if file_path.ex…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
