假设检验学习笔记
1. 假设检验的基本概念
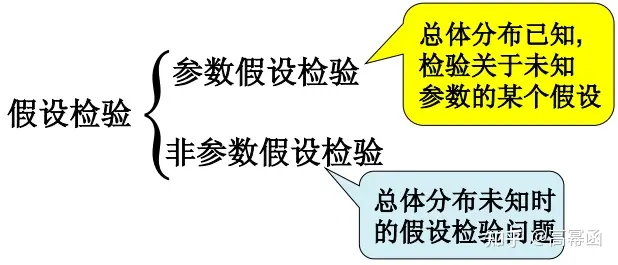
1.1. 原假设(零假设)
对总体的分布所作的假设用
表示,并称为原假设或零假设
在总体分布类型已知的情况下,仅仅涉及总体分布中未知参数的统计假设,称为参数假设
在总体分布类型未知的情况下,对总体分布类型或者总体分布的某些特性提出的统计假设,称为非参数假设
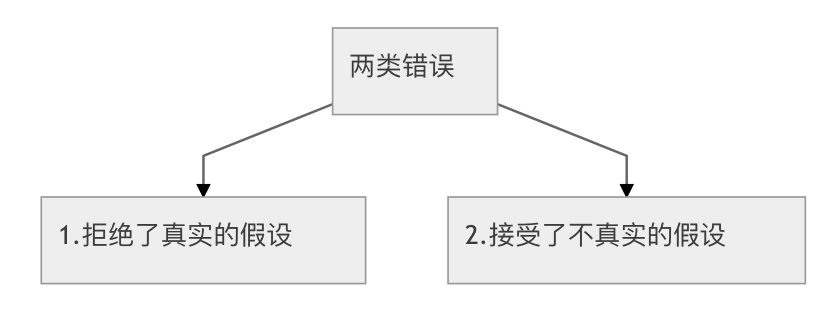
1.2. 假设检验中的两类错误
2. 单个正态总体参数的显著性检验
对假设
的一个检验法完全决定于小概率事件A的选择。
2.1. μ检验
- 已知
,检验
选择统计量
在成立的假定下,它服从N(0,1)分布。对给定的显著性水平
查表可得临界值,使得
这说明
为小概率事件
将样本值代人(1)式算出统计量的值u。如果,则表明在一次试验中小概率事件A出现了,因而拒绝
。这种检验法称为u检验。
已知方差时对正态总体均值的显著性检验归纳为以下几个步骤:
(1) 提出统计假设;
(2) 选择统计量,并从样本值计算出统计量的值u;
(3) 对给定的显著性水平,从附表 2 查出在
成立的条件下,满足等式
的临界值
;
(4) 作结论:如果,则拒绝
;反之,可接受
。
- 已知
,检验
选取统计量
并令
则,若
成立,还有
对给定的,由附表 2 可查得临界值
,使得
由式(2.2.5)可得
这说明事件“”是小概率事件。因此
的拒绝域为
,将样本值代人式(2)算出统计量的值u,若
,则拒绝
;否则可接受
。
2.2. t检验

 2.3. 卡方检验
2.3. 卡方检验

 3. 两个正态总体参数的显著性检验
3. 两个正态总体参数的显著性检验
3.1. F检验
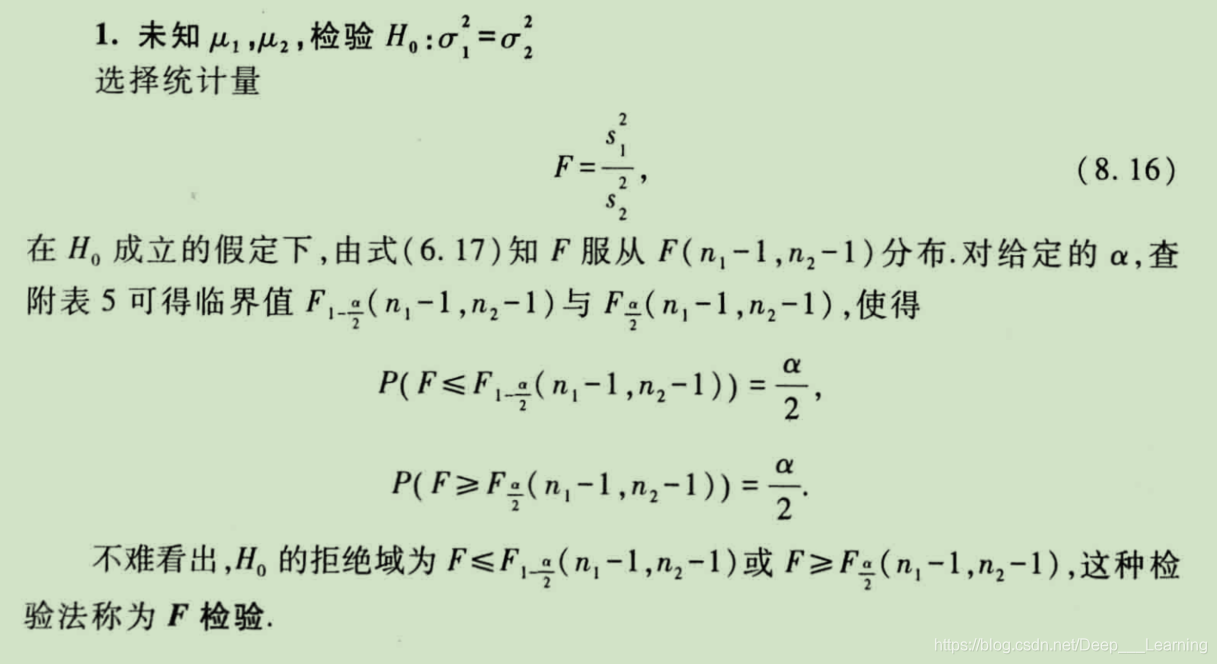
正态总体参数显著性检验表
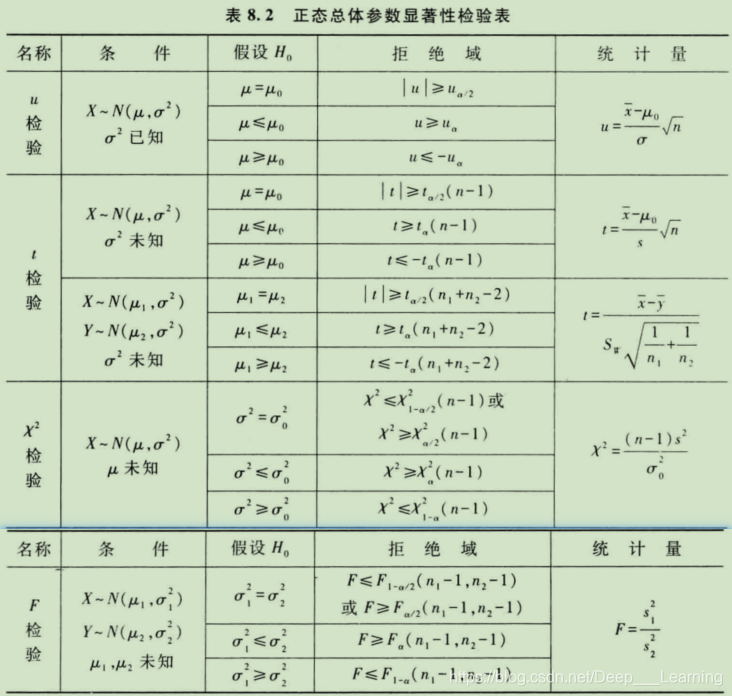
3.2. t检验


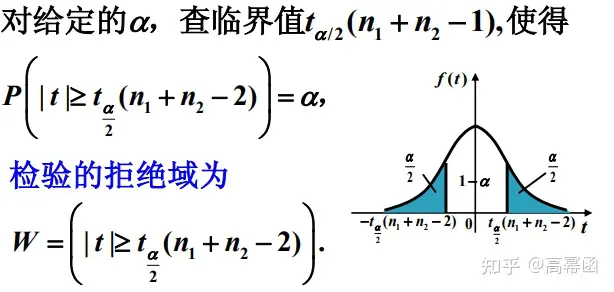


在假设检验中:
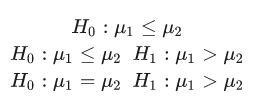
以上3种检验的检验法则与检验效果是一致的。

在假设检验中:

以上3种检验的检验法则与检验效果是一致的。
4. 非参数假设性检验
拟合优度检验
皮尔逊统计量
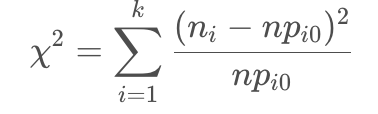

总结一下利用拟合优度检验来检验关于总体分布的假设,步骤如下:

参考文献
假设检验-CSDN博客
https://zhuanlan.zhihu.com/p/545859256
相关文章:

假设检验学习笔记
1. 假设检验的基本概念 1.1. 原假设(零假设) 对总体的分布所作的假设用表示,并称为原假设或零假设 在总体分布类型已知的情况下,仅仅涉及总体分布中未知参数的统计假设,称为参数假设 在总体分布类型未知的情况下&#…...

vue3 watch学习
watch的侦听数据源类型 watch的第一个参数为侦听数据源,有4种"数据源": ref(包括计算属性) reactive(响应式对象) getter函数 多个数据源组成的数组。 //ref const xref(0)//单个ref watch(x,(newX)>{console.…...

推荐的Pytest插件
推荐的Pytest插件 Pytest的插件生态系统非常丰富,以下是一些特别推荐的Pytest插件: pytest-sugar 这个插件改进了Pytest的默认输出,添加了进度条,并立即显示失败的测试。它不需要额外配置,只需安装即可享受更漂亮、更…...
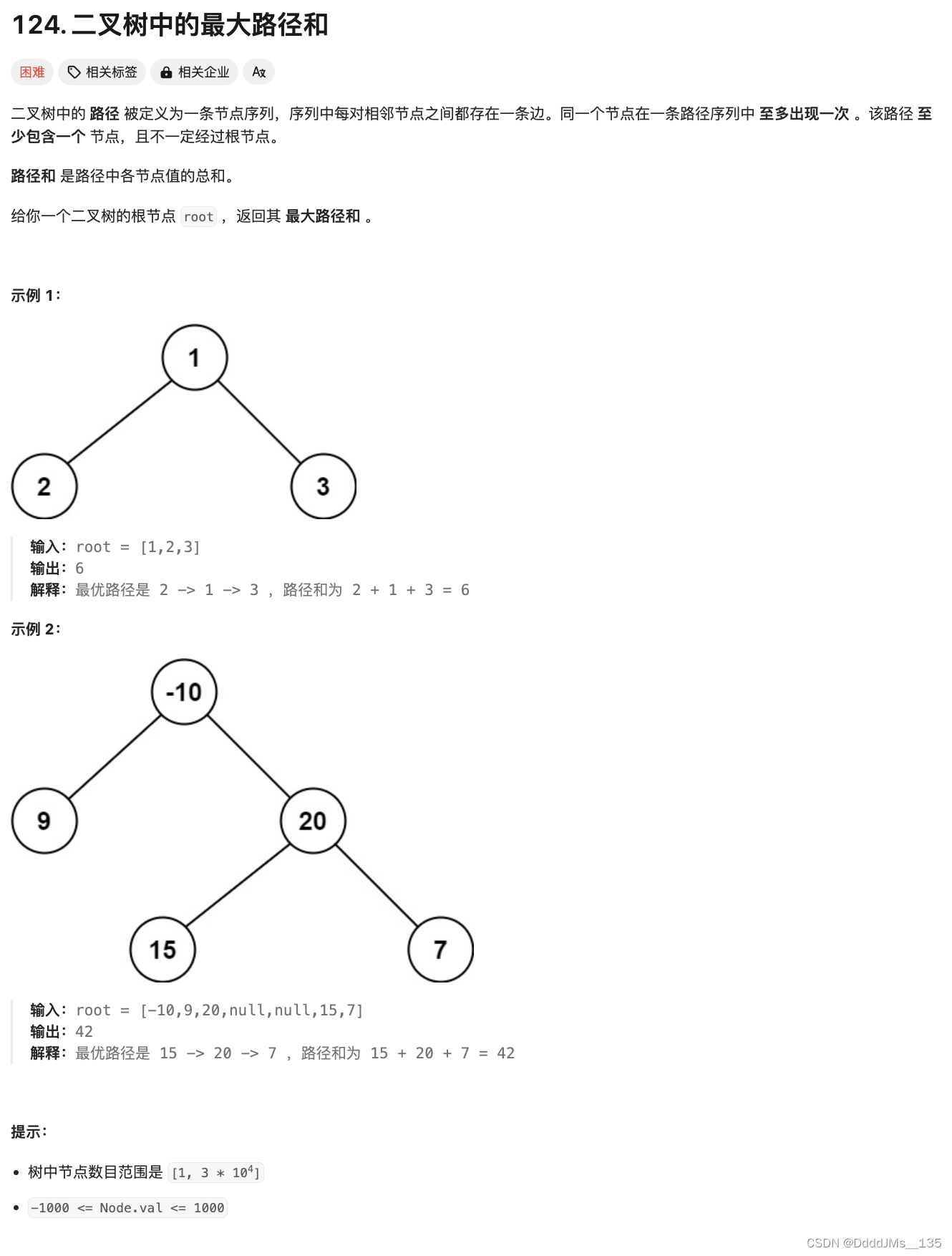
C语言 | Leetcode C语言题解之第124题二叉树中的最大路径和
题目: 题解: /*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ int max; int dfs(struct TreeNode* root){if(!root) return 0;int left dfs(root->left…...

Linux综合实践(Ubuntu)
目录 一、配置任务 1.1 配置该服务器的软件源为中科大软件源 1.2 安装相关软件openssh-server和vim 1.3 设置双网卡,网卡1为NAT模式,网卡2为桥接模式(桥接模式下,使用静态ip,该网卡数据跟实验室主机网络设置相似,除…...

C++面试题其二
19. STL中unordered_map和map的区别 unordered_map 和 map 都是C标准库中的关联容器,但它们在实现和性能方面有显著区别: 底层实现:map 是基于红黑树实现的有序关联容器,而 unordered_map 是基于哈希表实现的无序关联容器。元素…...
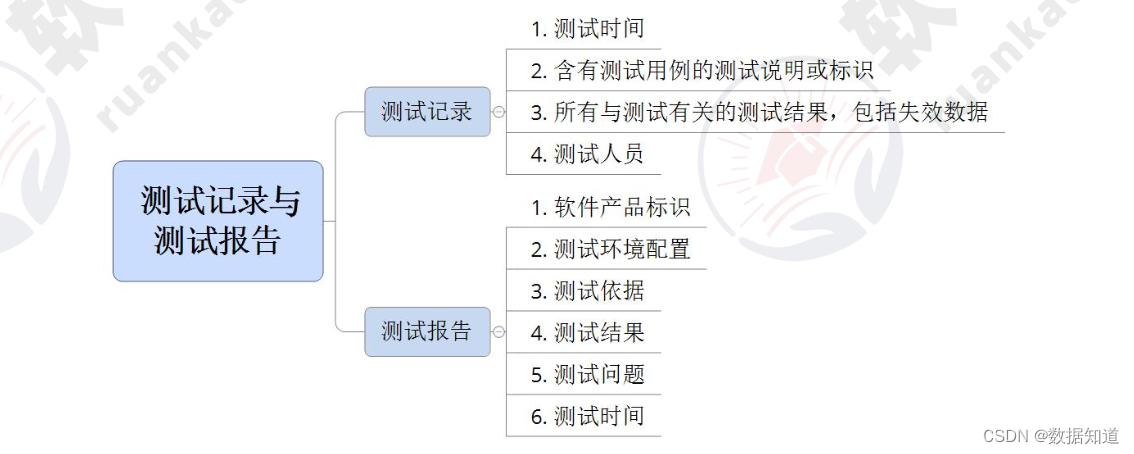
系统架构设计师【第9章】: 软件可靠性基础知识 (核心总结)
文章目录 9.1 软件可靠性基本概念9.1.1 软件可靠性定义9.1.2 软件可靠性的定量描述9.1.3 可靠性目标9.1.4 可靠性测试的意义9.1.5 广义的可靠性测试与狭义的可靠性测试 9.2 软件可靠性建模9.2.1 影响软件可靠性的因素9.2.2 软件可靠性的建模方法9.2.3 软件的可靠性模…...

x264 参考帧管理原理:i_poc_type 变量
x264 参考帧管理 x264 是一个开源的 H.264 视频编码软件,它提供了许多高级特性,包括对参考帧的高效管理。参考帧管理是视频编码中的一个重要部分,它涉及到如何存储、更新和使用已经编码的帧以提高编码效率。 x264 参考帧管理的一些关键点总结如下: 参考帧的初始化和重排序:…...

高级Web Lab2
高级Web Lab2 12 1 按照“Lab 2 基础学习文档”文档完成实验步骤 实验截图: 2 添加了Web3D场景选择按钮,可以选择目标课程或者学习房间。...
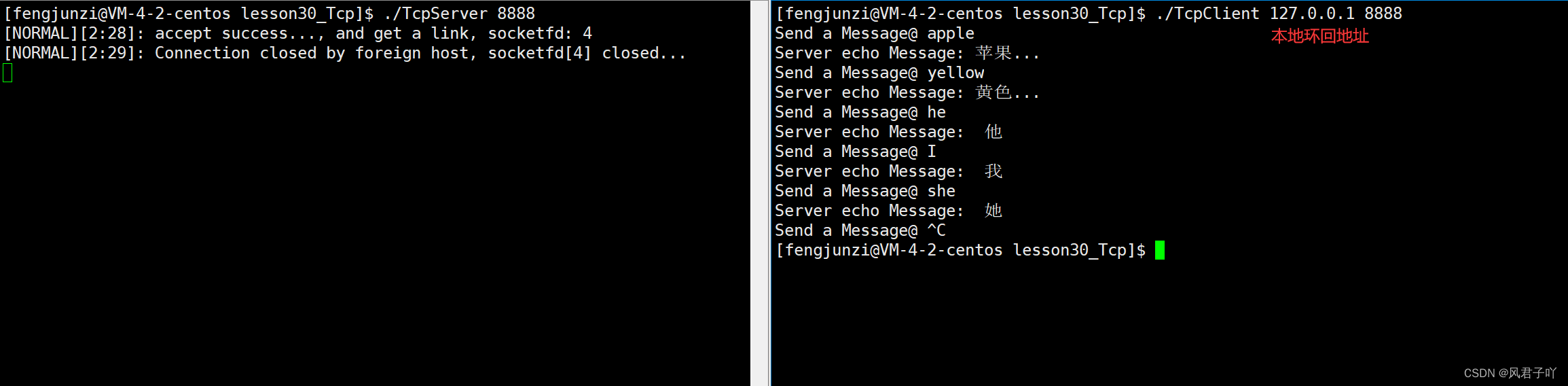
Linux网络-使用Tcp协议进行网络通信并通过网络接口实现远端翻译
文章目录 Tcp协议Tcp协议常见API接口1. int socket(int domain, int type, int protocol);2. int bind(int socket, const struct sockaddr *address, socklen_t address_len);struct sockaddr 3. int listen(int socket, int backlog);4. int accept(int socket, struct socka…...

实时数据传输:Django 与 MQTT 的完美结合
文章目录 准备工作创建 Django 项目与应用设置 MQTT 服务器编写 Django 视图编写前端模板发布 MQTT 消息运行 Django 项目 在当今互联网应用中,实时数据传输已经成为许多项目的核心需求。无论是社交媒体平台、在线游戏、金融交易还是物联网设备,都需要及…...

创建Django项目及应用
1 创建Project 1个Project可以对应多个app django-admin startproject myproject 2 创建App python manage.py startapp app01 INSTALLED_APPS [# ...app01,app02,# ... ] 如果要让这个应用在项目中起作用,需要在项目的 settings.py 文件的 INSTALLED_APPS 配置…...
)
Flutter课程分享 -(系统课程 基础 -> 进阶 -> 实战 仿京东商城)
前言 在移动应用开发的世界中,Flutter 作为一款由 Google 推出的开源 UI 软件开发工具包,正迅速赢得开发者们的青睐。其跨平台、高性能、丰富的组件库以及易于学习的特性,使得 Flutter 成为许多开发者的不二选择。然而,对于初学者…...

IDEA 中导入脚手架后该如何处理?
MySQL数据库创建啥的,没啥要说的!自行配置即可! 1.pom.xml文件,右键,add Maven Project …………(将其添加为Maven)【下述截图没有add Maven Project 是因为目前已经是Maven了!&…...

thinkphp6 queue队列的maxTries自定义
前景需求:在我们用队列的时候发现maxtries的个数时255次,这个太影响其他队列任务 我目前使用的thinkphp版本是6.1 第一部定义一个新的类 CustomDataBase(我用的mysql数据库存放的队列) 重写__make 和createPlainPayload方法 …...

【PHP项目实战训练】——laravel框架的实战项目中可以做模板的增删查改功能(2)
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...

Kotlin 对象
文章目录 对象表达式(匿名对象)对象的声明 对象表达式(匿名对象) 在 Kotlin 中可以使用object {}声明一个匿名的对象,我们无需声明这个对象的类: fun main() {val any object {fun greet() print("…...

力扣 142题 环形链表Ⅱ 记录
题目描述 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内…...

乐观锁 or 悲观锁 你怎么选?
你有没有听过这样一句话:悲观者正确,乐观者成功。那么今天我来分享下什么是乐观锁和悲观锁。 乐观锁和悲观锁有什么区别,它们什么场景会用 乐观锁 乐观锁基于这样的假设:多个事务在同一时间对同一数据对象进行操作的可能性很…...

《庆余年算法番外篇》:范闲通过最短路径算法在阻止黑骑截杀林相
剧情背景 在《庆余年 2》22集中,林相跟大宝交代完为人处世的人生哲理之后,就要跟大宝告别了 在《庆余年 2》23集中,林相在告老还乡的路上与婉儿和大宝告别后 范闲也在与婉儿的对话中知道黑骑调动是绝密,并把最近一次告老还乡梅…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
