LeetCode 2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法×3)
【LetMeFly】2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法×3)
力扣题目链接:https://leetcode.cn/problems/find-missing-and-repeated-values/
给你一个下标从 0 开始的二维整数矩阵 grid,大小为 n * n ,其中的值在 [1, n2] 范围内。除了 a 出现 两次,b 缺失 之外,每个整数都 恰好出现一次 。
任务是找出重复的数字a 和缺失的数字 b 。
返回一个下标从 0 开始、长度为 2 的整数数组 ans ,其中 ans[0] 等于 a ,ans[1] 等于 b 。
示例 1:
输入:grid = [[1,3],[2,2]] 输出:[2,4] 解释:数字 2 重复,数字 4 缺失,所以答案是 [2,4] 。
示例 2:
输入:grid = [[9,1,7],[8,9,2],[3,4,6]] 输出:[9,5] 解释:数字 9 重复,数字 5 缺失,所以答案是 [9,5] 。
提示:
2 <= n == grid.length == grid[i].length <= 501 <= grid[i][j] <= n * n- 对于所有满足
1 <= x <= n * n的x,恰好存在一个x与矩阵中的任何成员都不相等。 - 对于所有满足
1 <= x <= n * n的x,恰好存在一个x与矩阵中的两个成员相等。 - 除上述的两个之外,对于所有满足
1 <= x <= n * n的x,都恰好存在一对i, j满足0 <= i, j <= n - 1且grid[i][j] == x。
解题方法:计数(模拟)
开辟一个 n 2 + 1 n^2+1 n2+1的数组,用来记录每个数分别出现了多少次。
遍历原始数组即可完成计数数组,遍历计数数组即可得到答案。
- 时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 空间复杂度 O ( n 2 ) O(n^2) O(n2)
AC代码
C++
class Solution {
public:vector<int> findMissingAndRepeatedValues(vector<vector<int>>& grid) {vector<int> times(grid.size() * grid.size() + 1);for (vector<int>& line : grid) {for (int t : line) {times[t]++;}}vector<int> ans(2);for (int i = 1; i < times.size(); i++) {if (times[i] == 2) {ans[0] = i;}else if (times[i] == 0) {ans[1] = i;}}return ans;}
};
时间击败92.71%的提交,空间击败90.28%的提交。
其他方法
本题时间复杂度不可优化,说啥也得至少遍历一遍原始数组。如何优化空间复杂度呢?大致分为三种:
优化方法一:空间的原地使用:
例如 t t t出现过就将数组中第 t t t个元素置为负数,若某次将某元素置为负数时发现已经是负数了,则说明这个数出现了两次。到最后也没被置为负数的位置说明对应的数没有出现。
优化方法二:数学方法:
∑ i = 1 n 2 i − ∑ g r i d = b − a \sum_{i=1}^{n^2}i-\sum grid=b-a ∑i=1n2i−∑grid=b−a,一个方程不足以解出两个变量,因此可以再加一个方程。
例如 ∑ i = 1 n 2 i 2 − ∑ i ∈ g r i d i 2 = b 2 − a 2 \sum_{i=1}^{n^2}i^2-\sum_{i\in grid} i^2=b^2-a^2 ∑i=1n2i2−∑i∈gridi2=b2−a2,联立两方程即可得到 a a a和 b b b的值。
优化方法三:位运算:
根据异或的性质,异或一个数偶数次相当于没有异或。因此假设异或grid中的每个元素再异或从1到 n 2 n^2 n2得到结果 t t t,则 t = a ⊕ b t=a\oplus b t=a⊕b(相当于 a a a一共异或了3次而 b b b一共异或了1次)。
到这里很多同学都看出了这题本质和260. 只出现一次的数字 III相同。
如何拆分 a a a和 b b b?依据两个原则分别异或即可。假设 t t t二进制下第一个 1 1 1是第 2 2 2位,则所有数依据第 2 2 2位是否为 1 1 1分为两种。每组中所有元素相互异或,最终的两个结果就是 a a a和 b b b。
这里“所有数”是指 1 1 1到 n 2 n^2 n2的所有数以及原始数组中的所有数。
为什么这样能将 a a a和 b b b分开?因为根据异或结果 t t t可得, a a a和 b b b二进制下第 2 2 2位绝对不同,因此 a a a和 b b b会被分到两个不同的组中。每个组中除了 a a a或 b b b都出现偶数次,因此两组的异或结果就是 a a a和 b b b。
End
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/139357662
相关文章:
空间方法×3))
LeetCode 2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法×3)
【LetMeFly】2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法3) 力扣题目链接:https://leetcode.cn/problems/find-missing-and-repeated-values/ 给你一个下标从 0 开始的二维…...
)
【运维】VMware Workstation 虚拟机内无网络的解决办法(或许可行)
【使用桥接模式】 【重置网络】 这个过程涉及管理Linux系统中的网络驱动程序和网络管理工具。以下是每个步骤的详细解释: 卸载网络驱动模块: sudo rmmod e1000 sudo rmmod e1000e sudo rmmod igb这些命令使用 rmmod(remove moduleÿ…...
如何使用Dora SDK完成Fragment流式切换和非流式切换
我想大家对Fragment都不陌生,它作为界面碎片被使用在Activity中,如果只是更换Activity中的一小部分界面,是没有必要再重新打开一个新的Activity的。有时,即使要更换完整的UI布局,也可以使用Fragment来切换界面。 何…...
低代码开发平台(Low-code Development Platform)的模块组成部分
低代码开发平台(Low-code Development Platform)的模块组成部分主要包括以下几个方面: 低代码开发平台的模块组成部分可以按照包含系统、模块、菜单组织操作行为等维度进行详细阐述。以下是从这些方面对平台模块组成部分的说明: …...

Java网络编程(上)
White graces:个人主页 🙉专栏推荐:Java入门知识🙉 🙉 内容推荐:Java文件IO🙉 🐹今日诗词:来如春梦几多时?去似朝云无觅处🐹 ⛳️点赞 ☀️收藏⭐️关注💬卑微小博主&a…...

Spring Kafka 之 @KafkaListener 注解详解
我们在开发的过程中当使用到kafka监听消费的时候会使用到KafkaListener注解,下面我们就介绍下它的常见属性和使用。 一、介绍 KafkaListener 是 Spring Kafka 提供的一个注解,用于声明一个方法作为 Kafka 消息的监听器 二、主要参数 1、topic 描述&…...
【量算分析工具-贴地距离】GeoServer改造Springboot番外系列九
【量算分析工具-概述】GeoServer改造Springboot番外系列三-CSDN博客 【量算分析工具-水平距离】GeoServer改造Springboot番外系列四-CSDN博客 【量算分析工具-水平面积】GeoServer改造Springboot番外系列五-CSDN博客 【量算分析工具-方位角】GeoServer改造Springboot番外系列…...
文件操作及vi)
【linux】(1)文件操作及vi
文件和目录的创建 创建文件 touch 命令:创建一个新的空文件。 touch filename.txtecho 命令:创建一个文件并写入内容。 echo "Hello, World!" > filename.txtcat 命令:将内容写入文件。 cat > filename.txt然后输入内容&…...
【5】MySQL数据库备份-XtraBackup - 全量备份
MySQL数据库备份-XtraBackup-全量备份 前言环境版本 安装部署下载RPM 包二进制包 安装卸载 场景分析全量备份 | 恢复备份恢复综合 增量备份 | 恢复部分备份 | 恢复 前言 关于数据库备份的一些常见术语、工具等,可见《MySQL数据库-备份》章节,当前不再重…...

数据治理-数据标准演示
数据字典 数据标准-数据字典 词根 数据标准-词根 业务字典映射 数据标准-业务字典映射 标准文档 数据标准-标准文档...
基于Chisel的FPGA流水灯设计
Chisel流水灯 一、Chisel(一)什么是Chisel(二)Chisel能做什么(三)Chisel的使用(四)Chisel的优缺点1.优点2.缺点 二、流水灯设计 一、Chisel (一)什么是Chise…...

LabVIEW齿轮调制故障检测系统
LabVIEW齿轮调制故障检测系统 概述 开发了一种基于LabVIEW平台的齿轮调制故障检测系统,实现齿轮在恶劣工作条件下的故障振动信号的实时在线检测。系统利用LabVIEW的强大图形编程能力,结合Hilbert包络解调技术,对齿轮的振动信号进行精确分析…...

AI帮写:探索国内AI写作工具的创新与实用性
随着AI技术的快速发展,AI写作正成为创作的新风口。但是面对GPT-4这样的国际巨头,国内很多小伙伴往往望而却步,究其原因,就是它的使用门槛高,还有成本的考量。 不过,随着GPT技术的火热,国内也涌…...

n后问题 回溯笔记
问题描述 在nn格的棋盘上放置彼此不受攻击的n个皇后。 按照国际象棋的规则,皇后可以攻击与之处在同 一行或同一列或同一斜线上的棋子。n后问题等价于在nn格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。 代码 import java.uti…...

简述Java中实现Socket通信的步骤
在Java中,实现Socket通信通常涉及客户端和服务器端两个角色。以下是它们各自的基本步骤: 服务器端(Server) 创建ServerSocket对象: 在服务器端,首先需要创建一个ServerSocket对象。这个对象会监听来自客户…...
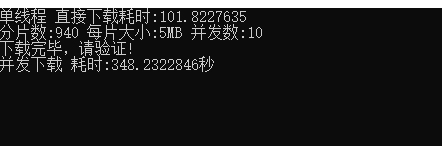
Asp.Net Core 实现分片下载的最简单方式
技术群里的朋友遇到了这个问题,起初的原因是他对文件增加了一个属性配置 fileResult.EnableRangeProcessing true;这个属性我从未遇到过,然后,去F1查看这个属性的描述信息也依然少的可怜,只有简单的描述为(获取或设置为 启用范围…...

[Mac软件]Leech for Mac v3.2 - 轻量级mac下载工具
黑果魏叔推荐Leech是由Many Tricks开发的适用于Mac OS X的轻量级且功能强大的下载管理器。 Leech让您完全控制下载,并与浏览器完全集成。您可以将下载排队,暂停和恢复,从受密码保护的服务器下载,并将密码存储在系统范围的安全钥匙…...
留给“端侧大模型”的时间不多了
端侧大模型(Edge AI models),也就是只在设备本地(如智能手机、IoT设备、嵌入式系统等)运行的大模型,过去一两年来非常流行。 具体表现在,终端设备厂商,如苹果、荣耀、小米、OV等&…...
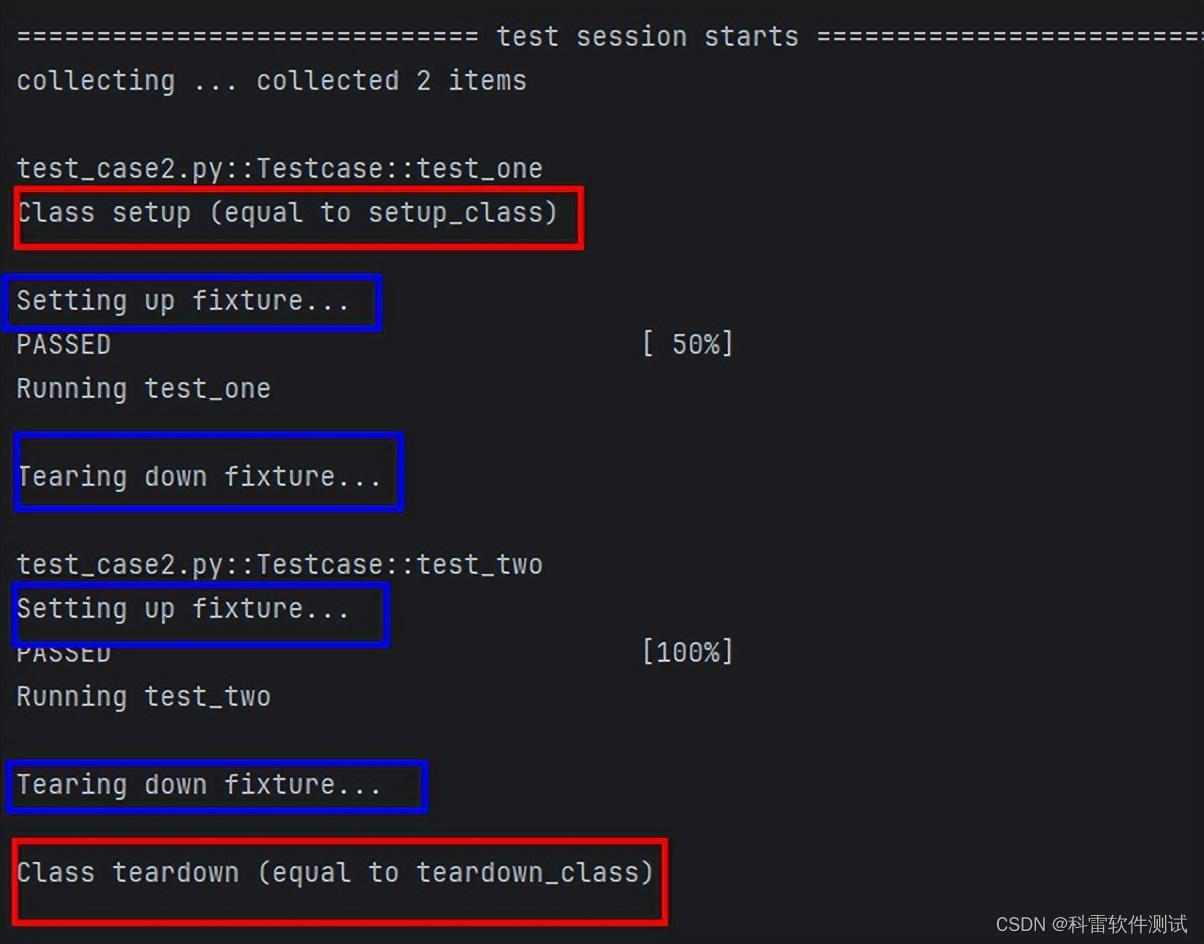
Pytest框架中的Setup和Teardown功能
在 pytest 测试框架中,setup 和 teardown是用于在每个测试函数之前和之后执行设置和清理的动作,而pytest 实际上并没有内置的 setup 和 teardown 函数,而是使用了一些装饰器或钩子函数来实现类似的功能。 学习目录 钩子函数(Hook…...

yolov10/v8 loss详解
v10出了就想看看它的loss设计有什么不同,看下来由于v8和v10的loss部分基本一致就放一起了。 v10的论文笔记,还没看的可以看看,初步尝试耗时确实有提升 好记性不如烂笔头,还是得记录一下,以免忘了,废话结束…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
