Spring boot实现基于注解的aop面向切面编程
Spring boot实现基于注解的aop面向切面编程
背景
从最开始使用Spring,AOP和IOC的理念就深入我心。正好,我需要写一个基于注解的AOP,被这个注解修饰的参数和属性,就会被拿到参数并校验参数。
一,引入依赖
当前spring boot版本为2.7.18,我引入的aspectjweaver版本为1.9.5。
<dependency><groupId>org.aspectj</groupId><artifactId>aspectjweaver</artifactId><version>1.9.5</version></dependency>
二,写注解
这个注解用来修饰方法,相当于一个切点,加上这个注解,这个方法就被被aop执行。
@Target({ElementType.METHOD})
@Retention(RetentionPolicy.RUNTIME)
public @interface ParamInterceptor {boolean checkParam() default true;
}
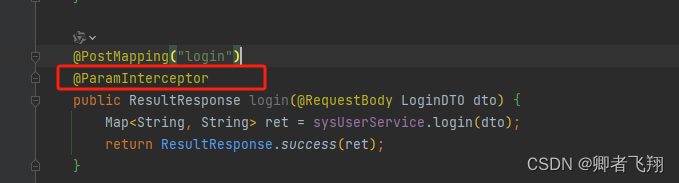
这个注解是用来修饰参数和属性的。被修饰的参数和属性在aop中会通过反射取出数据并判断
@Target({ElementType.PARAMETER, ElementType.FIELD})
@Retention(RetentionPolicy.RUNTIME)
public @interface VerifyParam {int min() default -1;int max() default -1;boolean required() default false;VerifyRegexEnum regex() default VerifyRegexEnum.NO;
}
这个是用到的VerifyRegexEnum 枚举类
@AllArgsConstructor
@Getter
public enum VerifyRegexEnum {NO("", "不校验"),IP("^((25[0-5]|2[0-4]\\d|1\\d\\d|[1-9]?\\d)(\\.(25[0-5]|2[0-4]\\d|1\\d\\d|[1-9]?\\d)){3})$", "ip地址"),POSITIVE_INTEGER("^\\d+$", "正整数"),NUMBER_LETTER_UNDER_LINE("\\w+$", "数字字母下划线"),PHONE("^1[3-9]\\d{9}$", "手机号"),EMAIL("^\\w+([-+.]\\w+)*@\\w+([-.]\\w+)*\\.\\w+([-.]\\w+)*$", "邮箱"),ID_CARD("^\\d{17}(\\d|x|X)$", "身份证"),PASSWORD("^[a-zA-Z0-9]{6,20}$", "密码"),MONEY("^\\d+(\\.\\d+)?$", "金额"),;private String regex;private String desc;public static boolean isMatch(String regex, String str) {return str.matches(regex);}}
三,编写切面aspect
该切面类就实现了,对参数和属性的校验。
@Aspect
@Component
@Slf4j
public class CdesAspect {@Before("@annotation(com.cdes.annotation.ParamInterceptor)")public void before(JoinPoint point) {Object[] args = point.getArgs();Method method = ((MethodSignature) point.getSignature()).getMethod();log.info("参数校验,方法名:{}",method.getName());ParamInterceptor paramInterceptor = method.getAnnotation(ParamInterceptor.class);if (paramInterceptor == null ) {return;}if(!paramInterceptor.checkParam()){return;}try{checkParam(method,args);}catch (Exception e){throw new BizException("400",e.getMessage());}}private void checkParam(Method method, Object[] args) throws IllegalAccessException {Parameter[] parameters = method.getParameters();for (int i = 0; i < parameters.length; i++) {Parameter parameter = parameters[i];Object paramValue = args[i];VerifyParam paramAnnotation = parameter.getAnnotation(VerifyParam.class);//取方法参数上的注解,如果有,则校验参数,如果没有,取该参数的属性,看是否有该注解if (paramAnnotation != null) {if(paramAnnotation.required() && paramValue == null){throw new BizException( "400",parameter.getName()+":参数不能为空");}if(paramAnnotation.max() != -1){if (paramValue.toString().length() > paramAnnotation.max()) {throw new BizException( "400",parameter.getName()+":参数长度不能超过"+paramAnnotation.max());}}if(paramAnnotation.min() != -1){if (paramValue.toString().length() < paramAnnotation.min()) {throw new BizException( "400",parameter.getName()+":参数长度不能小于"+paramAnnotation.min());}}if(paramAnnotation.regex() != null){if(!VerifyRegexEnum.isMatch(paramAnnotation.regex().getRegex(),paramValue.toString())){throw new BizException( "400",parameter.getName()+":参数不符合正则表达式");}}}else{//取属性上的注解,看是否需要校验Field[] fields = parameter.getClass().getDeclaredFields();if(fields == null || fields.length == 0){continue;}for (Field field : fields) {field.setAccessible(true);VerifyParam ann = field.getAnnotation(VerifyParam.class);if(ann == null){continue;}Object filedValue = field.get(paramValue);if(ann.required() && filedValue == null){throw new BizException( "400",field.getName()+":参数不能为空");}if(ann.max() != -1){if (filedValue.toString().length() > ann.max()) {throw new BizException( "400",field.getName()+":参数长度不能超过"+ann.max());}}if(ann.min() != -1){if (filedValue.toString().length() < ann.min()) {throw new BizException( "400",field.getName()+":参数长度不能小于"+ann.min());}}if(ann.regex() != null){if(!VerifyRegexEnum.isMatch(ann.regex().getRegex(),filedValue.toString())){throw new BizException( "400",field.getName()+":参数不符合正则表达式");}}}}}}
}
四,使用
controller中的login方法加上了ParamInterceptor注解,然后这个方法的入参LoginDTO中的属性加上了VerifyParam注解
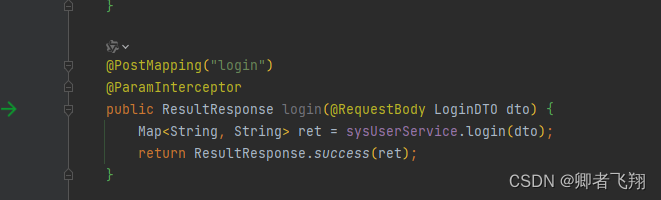
@Data
@AllArgsConstructor
@NoArgsConstructor
public class LoginDTO {@VerifyParam(regex = VerifyRegexEnum.PHONE)private String phone;@VerifyParam(regex = VerifyRegexEnum.PASSWORD)private String password;@VerifyParam(required = true)private String verifyCode;@VerifyParam(required = true)private String codeId;
}
总结
经过测试,校验参数功能正常。可以看到,spring boot的aop功能使用起来还是相当简单的。
相关文章:

Spring boot实现基于注解的aop面向切面编程
Spring boot实现基于注解的aop面向切面编程 背景 从最开始使用Spring,AOP和IOC的理念就深入我心。正好,我需要写一个基于注解的AOP,被这个注解修饰的参数和属性,就会被拿到参数并校验参数。 一,引入依赖 当前sprin…...

MySQL之查询性能优化(四)
查询性能优化 MySQL客户端/服务器通信协议 一般来说,不需要去理解MySQL通信协议的内部实现细节,只需要大致理解通信协议是如何工作的。MySQL客户端和服务器之间的通信协议是"半双工"的,这意味着,在任何一个时刻&#…...

定时任务详解
文章目录 定时任务详解JDK自带第三方任务调度框架java有哪些定时任务的框架为什么需要定时任务定时任务扫表的方案有什么缺点Quartzxxl-jobxxl-job详解 elastic-job 定时任务详解 在定时任务中,操作系统或应用程序会利用计时器或定时器来定期检查当前时间是否达到了…...
)
OnlyOffice DocumentServer 8.0.1编译破解版本(¥100)
OnlyOffice DocumentServer 8.0.1编译破解版本(¥100) 破解20人数限制 更换中文字体 修改源码,根据业务自定义服务 根据源码在本机启动项目,便于开发 将编译好的服务打包docker镜像运行 提供各种docker镜像包&…...

Android 应用权限
文章目录 权限声明uses-permissionpermissionpermission-grouppermission-tree其他uses-feature 权限配置 权限声明 Android权限在AndroidManifest.xml中声明,<permission>、 <permission-group> 、<permission-tree> 和<uses-permission>…...

MATLAB 匿名函数
定义匿名函数定义匿名函数的基本语法如下:示例示例 1:简单数学运算示例 2:字符串操作示例 3:作为参数传递 匿名函数的高级用法使用函数句柄定义多输出函数使用局部变量使用嵌套匿名函数 注意事项 匿名函数( Anonymous…...

Java 新手入门:基础知识点一览
Java 新手入门:基础知识点一览 想要踏入 Java 的编程世界?别担心,这篇文章将用简单易懂的表格形式,带你快速了解 Java 的基础知识点。 一、Java 是什么? 概念解释Java一种面向对象的编程语言,拥有跨平台、…...
三维模型轻量化工具:手工模型、BIM、倾斜摄影等皆可用!
老子云是全球领先的数字孪生引擎技术及服务提供商,它专注于让一切3D模型在全网多端轻量化处理与展示,为行业数字化转型升级与数字孪生应用提供成套的3D可视化技术、产品与服务。 老子云是全球领先的数字孪生引擎技术及服务提供商,它专注于让…...
小程序CI/CD之自动化打包预览并钉钉通知发布进程
小程序打包方式分为两种:手动打包、自动打包 那如何实现 自动打包 呐?我们今天就来聊一聊! 首先,很重要,看 官方文档 这里提到今天我们要聊的“主角” miniprogram-ci miniprogram-ci 是从微信开发者工具中抽离的关于…...

C++使用QtHttpServer开发服务端Server的Http POST接口和客户端Client示例
Client HTTP POST 假设http://127.0.0.1:8888/post/是一个能够接受POST请求的路径,我们想要向它提交一段json数据,用Qt可以这样实现: Suppose we want to make an HTTP POST with json body to http://127.0.0.1:8888/post/. QCoreApplica…...
计算机基础(8)——音频数字化(模电与数电)
💗计算机基础系列文章💗 👉🍀计算机基础(1)——计算机的发展史🍀👉🍀计算机基础(2)——冯诺依曼体系结构🍀👉ἴ…...
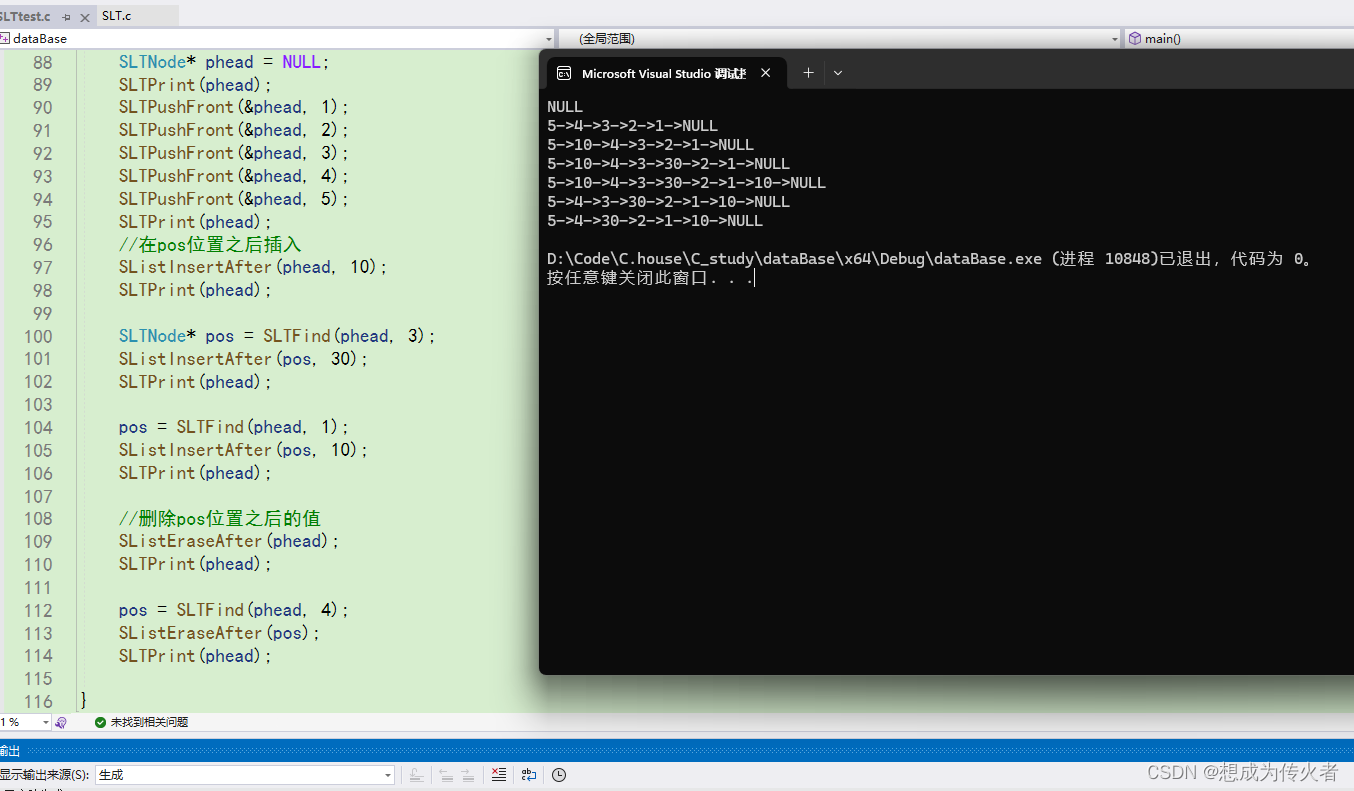
手搓单链表(无哨兵位)(C语言)
目录 SLT.h SLT.c SLTtest.c 测试示例 单链表优劣分析 SLT.h #pragma once#include <stdio.h> #include <assert.h> #include <stdlib.h>typedef int SLTDataType;typedef struct SListNode {SLTDataType data;struct SListNode* next; }SLTNode;//打印…...

代码随想录算法训练营第18天|二叉树
513. 找树左下角的值 最左边的结点的特性 1.只能是叶子结点, 2.必须考虑是最底层,所以要考虑树的深度 3.同样的深度考虑左子树 考虑迭代法,层序遍历 递归优点难搞的 /*** Definition for a binary tree node.* function TreeNode(val, left, righ…...

使用tftpd更新开发板内核
我们升级内核可以通过原厂提供的升级软件来进行,比如瑞芯微的RKDevTool.exe,只不过这种方式必须通过指定的OTG升级口,还得借助按键进入loader模式后才可以。 其实还可以利用一些通用的工具来进行升级,比如tftpd工具。 下载地址p…...

MySQL数据库整体知识点简述
目录 第一章:数据库系统概述 第二章:信息与数据模型 第3章 关系模型与关系规范化理论 第四章——数据库设计方法 第六-七章——MySQL存储引擎与数据库操作管理 第九章——索引 第10章——视图 第11章——MySQL存储过程与函数 第12章——MySQL 触…...
深入理解MySQL索引下推优化
在MySQL中,索引的使用对于查询性能至关重要。然而,即使有合适的索引,有时查询性能仍然不尽如人意。索引下推(Index Condition Pushdown,ICP)是一项能够进一步优化查询性能的技术。本文将详细讲解索引下推的…...
论文降重技巧:AI工具如何助力论文原创性提升?
论文降重一直是困扰各界毕业生的“拦路虎”,还不容易熬过修改的苦,又要迎来降重的痛。 其实想要给论文降重达标,我有一些独家秘诀。话不多说直接上干货! 1、同义词改写(针对整段整句重复) 这是最靠谱也是…...
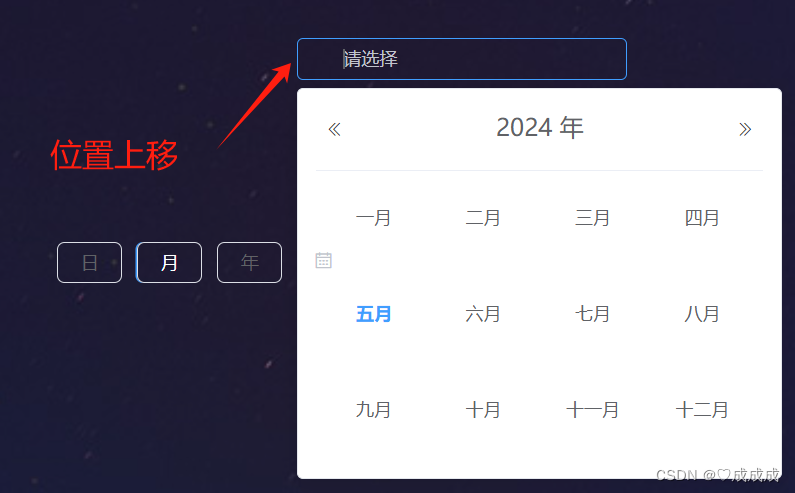
el-date-picker的使用,及解决切换type时面板样式错乱问题
这里选择器的类型可以选择日月年和时间范围,根据类型不同,el-date-picker的面板也展示不同,但是会出现el-date-picker错位,或者面板位置和层级等问题。 源代码: <el-selectv-model"dateType"placeholder&…...

Flutter 中的 ToggleButtonsTheme 小部件:全面指南
Flutter 中的 ToggleButtonsTheme 小部件:全面指南 Flutter,作为由 Google 开发的跨平台 UI 框架,为开发者提供了丰富的组件来构建现代化的应用程序。ToggleButtons 是 Material Design 组件库中的一个组件,它允许用户从一组选项…...
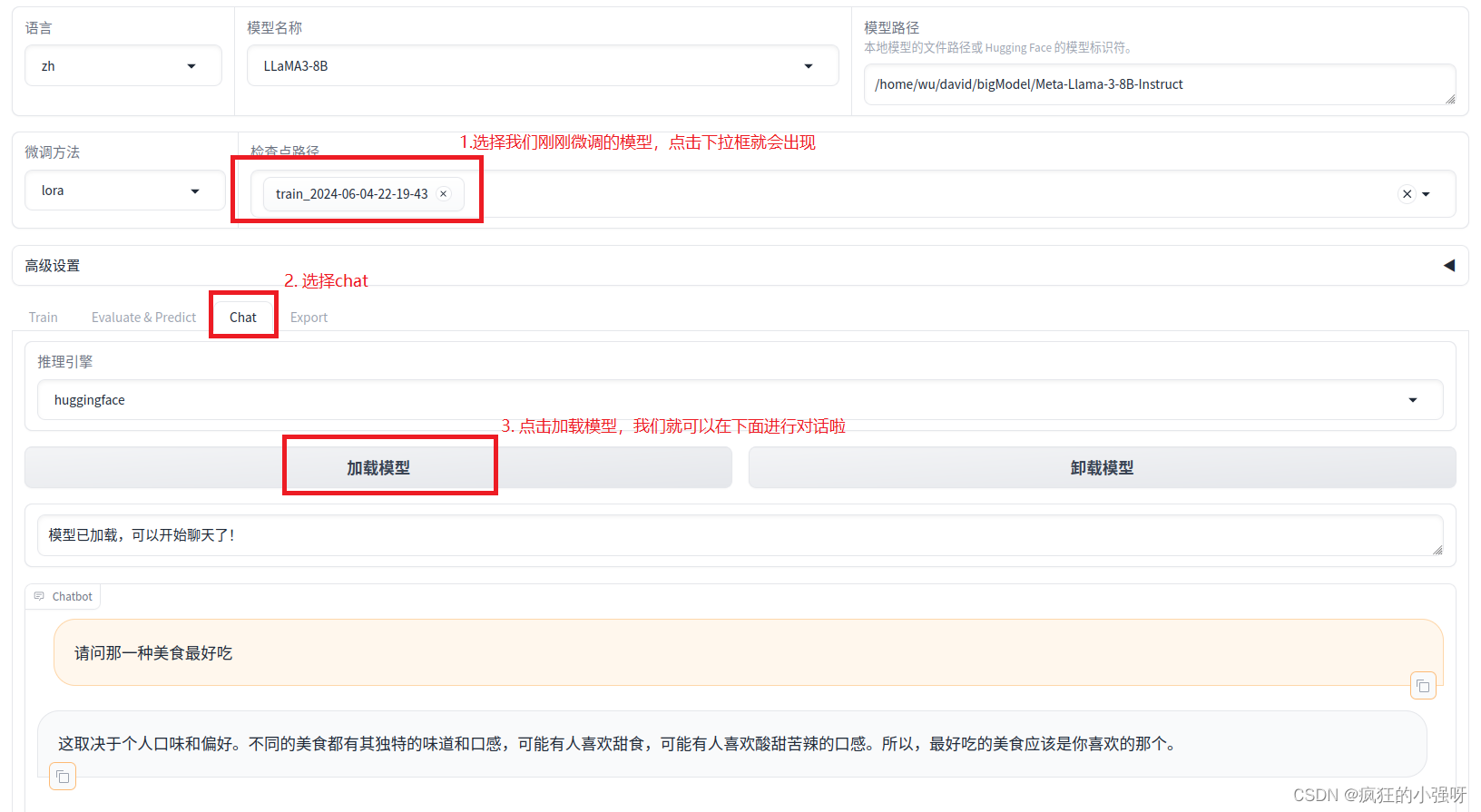
新手教程之使用LLaMa-Factory微调LLaMa3
文章目录 为什么要用LLaMa-Factory什么是LLaMa-FactoryLLaMa-Factory环境搭建微调LLaMA3参考博文 为什么要用LLaMa-Factory 如果你尝试过微调大模型,你就会知道,大模型的环境配置是非常繁琐的,需要安装大量的第三方库和依赖,甚至…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
