当前位置： 首页 > news >正文

pidstat -d 1分析磁盘吞吐量

news 2026/2/8 7:33:04

iostat -dx 1 查看磁盘IO吞吐量

pidstat -d 1看是哪个进程写的

相关文章：

pidstat -d 1分析磁盘吞吐量

iostat -dx 1 查看磁盘IO吞吐量 pidstat -d 1看是哪个进程写的...

编程日记 2024/6/5 11:04:48

期望20K，2年golang深圳某互联网小公司一面

后续约了二面（CTO面），需要到现场，基本没问啥具体的技术知识，都是聊规划和个人职业目标 一面 1、假设访问百度网站，从在浏览器输入网址，到最终页面展示出来，中间会发生哪些事情&…...

编程日记 2024/6/5 11:03:46

#02 安装指南：如何配置Stable Diffusion环境

文章目录 前言前置条件第1步：安装Python和PIP第2步：创建虚拟环境第3步：安装PyTorch和CUDA第4步：安装Stable Diffusion相关库第5步：测试环境结论 前言 在之前的文章中，我们介绍了Stable Diffusion基础入门和…...

编程日记 2024/6/5 11:02:45

拼多多笔试

拼多多2022数据分析笔试（0822） 一、选择题 1.已知样本量n，样本均值及方差求置信区间 2.决策树 3.峰度系数 4.协方差 5.第一、第二熵变 6.充分统计量 7.xgboost 8.方差分析中的多重比较 二、编程题 1. 一张用户点击路径的表&#x…...

编程日记 2024/6/5 11:01:42

Golang | Leetcode Golang题解之第119题杨辉三角II

题目&#xff1a; 题解&#xff1a; func getRow(rowIndex int) []int {row : make([]int, rowIndex1)row[0] 1for i : 1; i < rowIndex; i {row[i] row[i-1] * (rowIndex - i 1) / i}return row }...

编程日记 2024/6/5 10:59:39

Flutter 中的 SliverIgnorePointer 小部件：全面指南

Flutter 中的 SliverIgnorePointer 小部件&#xff1a;全面指南 Flutter 是一个由 Google 开发的跨平台 UI 框架&#xff0c;它提供了一系列的组件来帮助开发者构建高性能、美观的移动、Web 和桌面应用。在 Flutter 的滚动组件中&#xff0c;SliverIgnorePointer 是一个用来包…...

编程日记 2024/6/5 10:58:37

比较两台计算机上的LabVIEW、工具包及驱动程序的一致性

比较两台计算机上的LabVIEW、工具包及驱动程序是否相同&#xff0c;可以通过以下步骤实现&#xff1a; 1. 检查LabVIEW版本 方法一&#xff1a;在LabVIEW中查看版本信息 步骤&#xff1a; 打开LabVIEW。点击菜单栏的 Help > About LabVIEW。记录显示的LabVIEW版本号和许可…...

编程日记 2024/6/5 10:54:31

参考——温湿度传感器DHT11驱动_STM32

设备&#xff1a;stm32f407ZGT6 环境&#xff1a;FreeRTOS HAL 到网上找DHT11的驱动&#xff0c;但是都无法使用。原因是RTOS环境中&#xff0c;由于多线程&#xff0c;使用循环计数阻塞式的delay_us延时函数就没那么准&#xff0c;且不同设备中delay_us的计数值不一样…...

编程日记 2024/6/5 10:50:25

架构每日一学 14：架构师如何进行可行性探索？

架构活动中&#xff0c;如果不进行可行性探索可能会导致重大失误&#xff0c;为企业发展带来风险。 可行性探索是架构活动的最后一个节点&#xff0c;在这之后的架构活动就像是离弦之箭&#xff0c;即便发现重大风险也很难再回头了。 互联网公司之间的竞争非常激烈&#xff0…...

编程日记 2024/6/5 10:48:22

多线程知识-13

为什么应该在循环中检查等待条件 为了实现多线程的同步和协调&#xff0c;通常使用等待和唤醒机制。在等待和唤醒机制中&#xff0c;等待条件是指一个线程等待某个条件的满足&#xff0c;当条件满足时&#xff0c;线程被唤醒继续执行。 在循环中检查等待条件的目的是为了避免虚…...

编程日记 2024/6/5 10:46:20

vue3+cli-service配置代理，跨域请求

一、配置代理端口和代理转发 在vue.config.js文件中 const {defineConfig} require(vue/cli-service)module.exports defineConfig({devServer: {host: 0.0.0.0,port: 8088, // 启动端口号proxy: {/api: { // 请求接口中要替换的标识target: , // 代理地址&#xff0c;后…...

编程日记 2024/6/5 10:44:18

git介绍、安装、配置

文章目录 1. GIT介绍2. 使用GIT的好处3. GIT 安装4. GIT 配置4.1 GIT 初始化设置、命令别名设置4.2 如果终端安装了oh-my-zsh&#xff0c;会带一堆git命令别名4.3 GIT配置文件介绍4.3.1 Linux、Mac OS系统4.3.2 windows系统 5. git设置远程仓库账号密码(拉取、上传代码不用输入…...

编程日记 2024/6/5 10:42:14

打开flutter调试

debugPaintSizeEnabled true; debugPaintBaselinesEnabled true;...

编程日记 2024/6/5 10:41:12

【前端 - Vue】Vuex基础入门，创建仓库的详细步骤

&#x1f680; 个人简介&#xff1a;6年开发经验&#xff0c;现任职某国企前端负责人&#xff0c;分享前端相关技术与工作常见问题~ &#x1f49f; 作 者&#xff1a;前端菜鸟的自我修养❣️ &#x1f4dd; 专 栏&#xff1a;vue从基础到起飞 &#x1f308; 若有帮助&…...

编程日记 2024/6/5 10:39:10

#01 Stable Diffusion基础入门：了解AI图像生成

文章目录 前言什么是Stable Diffusion?Stable Diffusion的工作原理如何使用Stable Diffusion?Stable Diffusion的应用场景结论 前言 在当今迅速发展的人工智能领域&#xff0c;AI图像生成技术以其独特的魅力吸引了广泛的关注。Stable Diffusion作为其中的一项前沿技术&#…...

编程日记 2024/6/5 10:38:08

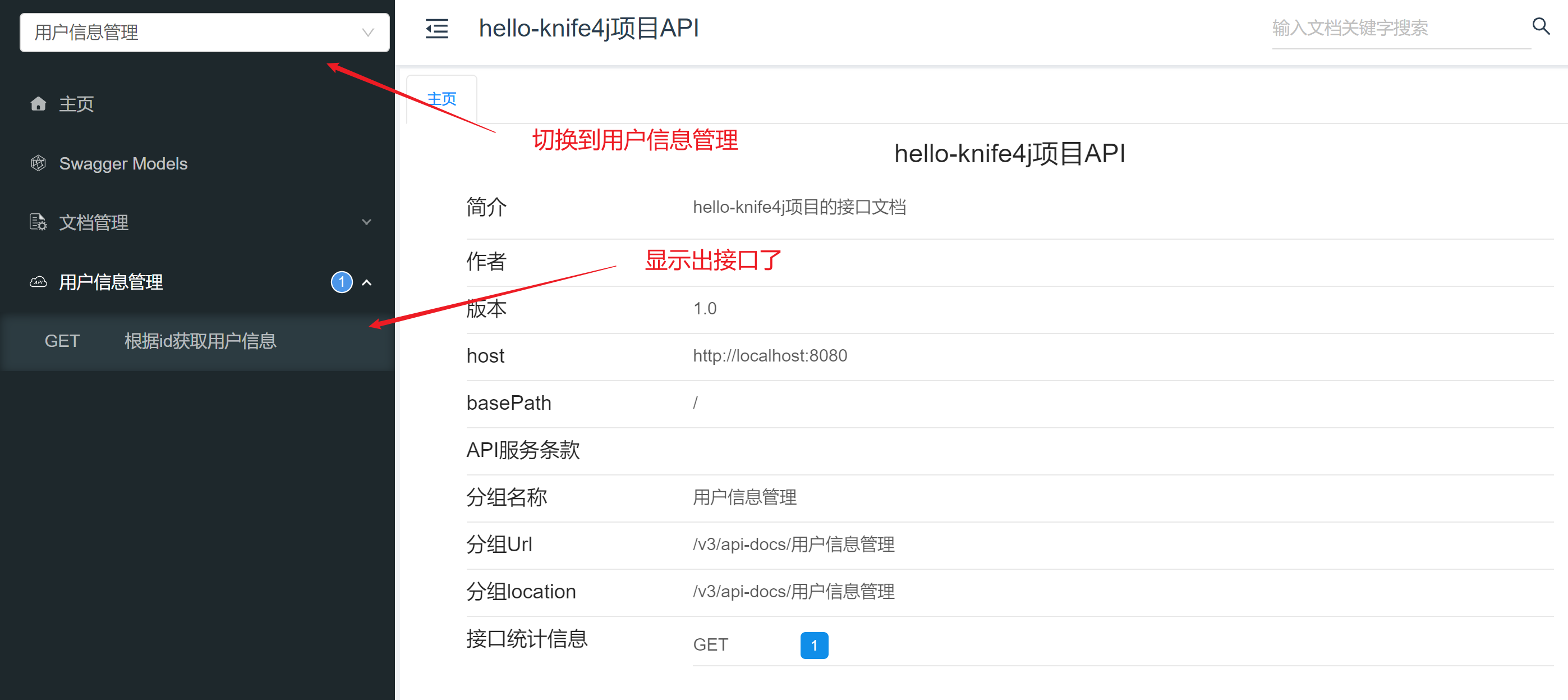
Knife4j使用

Knife4j使用 文章目录 Knife4j使用1、Knife4j介绍2、SpringBoot集成Knife4j3、基本使用 1、Knife4j介绍 Knife4j是一个用于生成和展示API文档的工具&#xff0c;同时它还提供了在线调试的功能&#xff0c;可以看作是Swagger的升级版&#xff0c;界面也比Swagger更好看&#xf…...

编程日记 2024/6/5 10:35:04

一文读懂银行承兑汇票：从申请到使用全攻略

银行承兑汇票&#xff08;Banks Acceptance Bill&#xff0c;BA&#xff09;是商业汇票的一种。它是由在承兑银行开立存款账户的存款人出票&#xff0c;向开户银行申请并经银行审查同意承兑的&#xff0c;保证在指定日期无条件支付确定的金额给收款人或持票人的票据。银行承兑汇…...

编程日记 2024/6/5 10:31:55

唯众智联网（AIoT）应用开发教学实训解决方案

一、引言 随着信息技术的飞速发展&#xff0c;物联网&#xff08;IoT&#xff09;和人工智能&#xff08;AI&#xff09;技术逐渐融合&#xff0c;形成了智联网&#xff08;AIoT&#xff09;这一新兴领域。智联网通过智能化设备、传感器、云计算等技术手段&#xff0c;实现了数…...

编程日记 2024/6/5 10:30:54

归纳跨域几种解决方案

什么是跨域&#xff1f; **说起跨域&#xff0c;就要知道什么是浏览器同源策略 **浏览器同源策略&#xff1a;必须是协议、域名、端口完全一致的才符合同源策略 **如果以上三项&#xff0c;有一项不同都涉及到跨域问题 为什么浏览器要设置同源策略呢&#xff1f; 没有同源策…...

编程日记 2024/6/5 10:29:53

LeetCode刷题第3题（C#）

给定一个字符串 s &#xff0c;请你找出其中不含有重复字符的 最长子串的长度。 法一&#xff1a; 这道题用到的其实是滑动窗口。 滑动窗口算法是在特定窗口大小的数组或字符串上执行要求的操作。它可以将一部分问题中的嵌套循环转变为一个单循环&#xff0c;以此减少时间复…...

编程日记 2024/6/5 10:28:51

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)

题目&#xff1a;3442. 奇偶频次间的最大差值 I 思路 &#xff1a;哈希&#xff0c;时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况&#xff0c;哈希表这里用数组即可实现。 C版本&#xff1a; class Solution { public:int maxDifference(string s) {int a[26]…...

编程新知 2026/2/7 23:18:31

深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法

深入浅出&#xff1a;JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中&#xff0c;随机数的生成看似简单&#xff0c;却隐藏着许多玄机。无论是生成密码、加密密钥&#xff0c;还是创建安全令牌&#xff0c;随机数的质量直接关系到系统的安全性。Jav…...

编程新知 2025/10/8 4:56:09

汽车生产虚拟实训中的技能提升与生产优化​

在制造业蓬勃发展的大背景下&#xff0c;虚拟教学实训宛如一颗璀璨的新星&#xff0c;正发挥着不可或缺且日益凸显的关键作用&#xff0c;源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例&#xff0c;汽车生产线上各类…...

编程新知 2026/1/27 7:46:36

【项目实战】通过多模态+LangGraph实现PPT生成助手

PPT自动生成系统 基于LangGraph的PPT自动生成系统&#xff0c;可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析&#xff1a;自动解析Markdown文档结构PPT模板分析&#xff1a;分析PPT模板的布局和风格智能布局决策&#xff1a;匹配内容与合适的PPT布局自动…...

编程新知 2026/2/3 22:50:07

聊一聊接口测试的意义有哪些？

目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开&#xff0c;首…...

编程新知 2025/10/14 6:46:13

无人机侦测与反制技术的进展与应用

国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机&#xff08;无人驾驶飞行器&#xff0c;UAV&#xff09;技术的快速发展&#xff0c;其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统&#xff0c;无人机的“黑飞”&…...

编程新知 2026/1/26 6:01:03

mac：大模型系列测试

0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何&#xff0c;是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试&#xff0c;是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

编程新知 2026/2/4 0:46:21

LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别（二）

在上一篇文章中，我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调，以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后，如何调用这个模型进行人脸情感识别的具体代码实现，包括详细的步骤和注释。 模型调用步骤 环境准备：确保安装了必要的Python库。…...

编程新知 2025/11/4 0:47:29

五子棋测试用例

一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏&#xff0c;有着深厚的文化底蕴。通过将五子棋制作成网页游戏&#xff0c;可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家&#xff0c;都可以通过网页五子棋感受到东方棋类…...

编程新知 2026/2/1 21:56:50

QT开发技术【ffmpeg + QAudioOutput】音乐播放器

一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下&#xff0c;音视频内容犹如璀璨繁星&#xff0c;点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频&#xff0c;到在线课堂中知识渊博的专家授课&#xff0c;再到影视平台上扣人心弦的高清大片&#xff0c;音…...

编程新知 2026/2/4 5:32:18