双指针法 ( 三数之和 )
题目 :给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
在解决这一问题中,我们需要用到相向双指针。
首先需要对数组nums 排好序,便于之后的各种操作。

从数组第一个数num[now] 开始向后遍历, 如果now now+1 now+2 三个数和大于0,在这种情况下,当前剩下的最小的三个数和仍大于0,那么便没有能使之后的数的和都大于0,结束循环;同样,如果now end end-1 三个数的和小于0,在这种情况下,当前数 与剩下的最大的两个数和仍小于0,那么便没有能使之后的数的和都小于0,now++,进行下一次判断;如果num[now] 与上一个数相同,now++,进行下一次判断。 将数组排序好的好处之一便在此。需要注意的是,now 在整个循环中应当小于 size - 2 ,因为最少应剩下三个数。
在有一个符合上述条件的now 时:

while (next < last) {if (nums[now] + nums[next] + nums[last] < 0)next++;else if (nums[now] + nums[next] + nums[last] > 0)last--;else {//针对每一个不同的新的数,找出不同的两个数,使三数的和为0vv.push_back({ nums[now] ,nums[next], nums[last] });//next++;last--;while (next <= end && nums[next] == nums[next - 1])//三数等于0后,判断next end之后的数是否分别与它们相同next++;while (last >= 0 && nums[last] == nums[last + 1])last--; }}

class Solution {
public: vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> vv;sort(nums.begin(),nums.end());int now = 0;while (now < nums.size() - 2) {int end = nums.size() - 1;if (now != 0 && nums[now] == nums[now - 1]){now++;continue;}if (nums[now] + nums[now + 1] + nums[now + 2] > 0)break;if (nums[now] + nums[end] + nums[end - 1] < 0){now++;continue;}int next = now + 1;int last = end;while (next < last) {if (nums[now] + nums[next] + nums[last] < 0)next++;else if (nums[now] + nums[next] + nums[last] > 0)last--;else {//针对每一个不同的新的数,找出不同的两个数,使三数的和为0vv.push_back({ nums[now] ,nums[next], nums[last] });//next++;last--;while (next <= end && nums[next] == nums[next - 1])//三数等于0后,判断next end之后的数是否分别与它们相同next++;while (last >= 0 && nums[last] == nums[last + 1])last--; }}now++;}return vv;}
};
相关文章:

双指针法 ( 三数之和 )
题目 :给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复…...

感染恶意代码之后怎么办?
隔离设备 立即将感染设备与网络隔离,断开与互联网和其他设备的连接。这可以防止恶意代码进一步传播到其他设备,并减少对网络安全的威胁。 确认感染 确认设备是否真的感染了恶意代码。这可能需要使用安全软件进行全面扫描,以检测和识别任何已…...
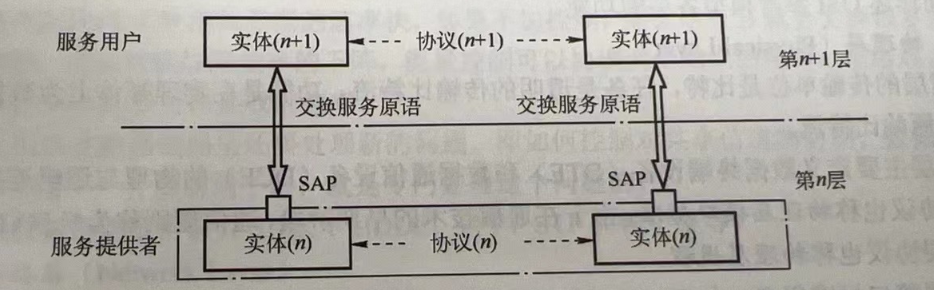
【计算机网络】P3 计算机网络协议、接口、服务的概念、区别以及计算机网络提供的三种服务方式
目录 协议什么是协议协议是水平存活的协议的组成 接口服务服务是什么服务原语 协议与服务的区别计算机网络提供的服务的三种方式面向连接服务与无连接服务可靠服务与不可靠服务有应答服务与无应答服务 协议 什么是协议 协议,就是规则的集合。 在计算机网络中&…...

多角度剖析事务和事件的区别
事务和事件这两个概念在不同的领域有着不同的含义,尤其是在计算机科学、数据库管理和软件工程中。下面从多个角度来剖析事务和事件的区别: 计算机科学与数据库管理中的事务 事务(Transaction): 定义:在数据库管理中,…...
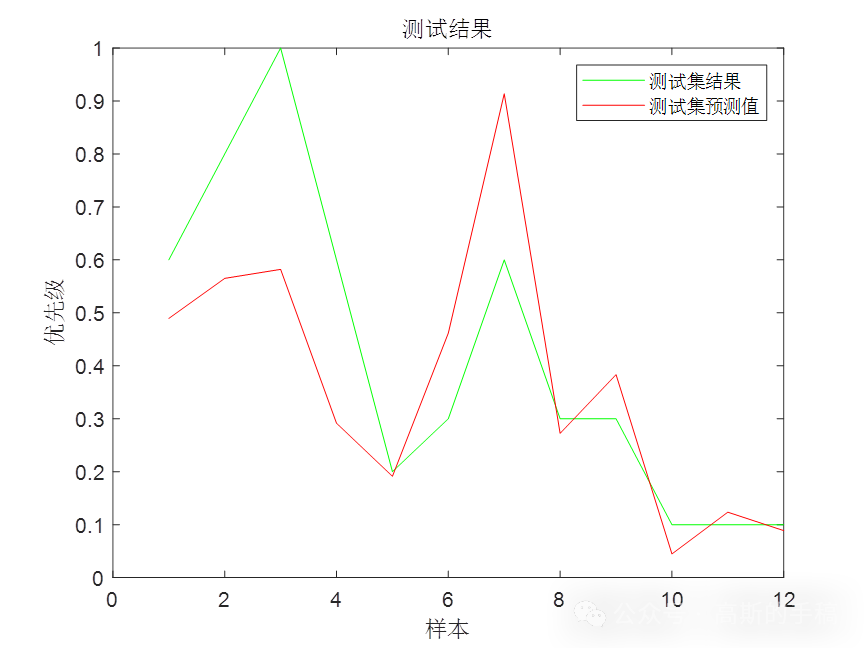
模糊小波神经网络(MATLAB 2018)
模糊系统是一种基于知识或规则的控制系统,从属于智能控制,通过简化系统的复杂性,利用控制法来描述系统变量之间的关系,采用语言式的模糊变量来描述系统,不必对被控对象建立完整的数学模型。相比较传统控制策略…...

HTML布局
标准流: 标准流就是元素在页面中的默认排列方式,也就是元素在页面中的默认位置。 1.1 块元素----独占一行----从上到下排列 1.2 行内元素----不独占一行----从左到右排列,遇到边界换行 1.3 行内块元素----不独占一行…...

数据结构:双链表
数据结构:双链表 题目描述参考代码 题目描述 输入样例 10 R 7 D 1 L 3 IL 2 10 D 3 IL 2 7 L 8 R 9 IL 4 7 IR 2 2输出样例 8 7 7 3 2 9参考代码 #include <iostream>using namespace std;const int N 100010;int m; int idx, e[N], l[N], r[N];void init…...

Python3 元组、列表、字典、集合小结
前言 本文主要对Python中的元组、列表、字典、集合进行小结,主要内容包括知识点回顾、异同点、使用场景。 文章目录 前言一、知识点回顾1、列表(List)2、 元组(Tuple)3、 字典(Dictionary)4.、…...

2024会声会影破解免费序列号,激活全新体验!
会声会影2024序列号注册码是一款专业的视频编辑软件,它以其强大的功能和易用性受到了广大用户的喜爱。在这篇文章中,我将详细介绍会声会影2024序列号注册码的功能和特色,帮助大家更好地了解这款产品。 会声会影全版本绿色安装包获取链接&…...
机器学习18个核心算法模型
1. 线性回归(Linear Regression) 用于建立自变量(特征)和因变量(目标)之间的线性关系。 核心公式: 简单线性回归的公式为: , 其中 是预测值, 是截距, 是斜…...
)
平滑值(pinghua)
平滑值 题目描述 一个数组的“平滑值”定义为:相邻两数差的绝对值的最大值。 具体的,数组a的平滑值定义为 f ( a ) m a x i 1 n − 1 ∣ a i 1 − a i ∣ f(a)max_{i1}^{n-1}|a_{i1}-a_i| f(a)maxi1n−1∣ai1−ai∣ 现在小红拿到了一个数组…...
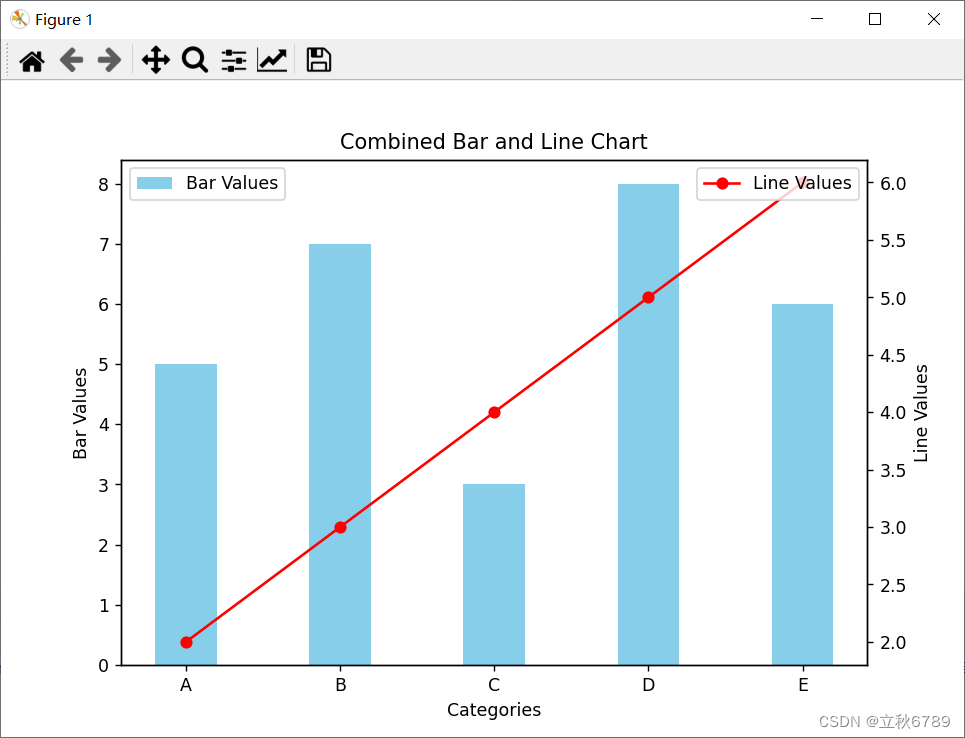
使用matplotlib绘制折线条形复合图
使用matplotlib绘制折线条形复合图 介绍效果代码 介绍 在数据可视化中,复合图形是一种非常有用的工具,可以同时显示多种数据类型的关系。在本篇博客中,我们将探讨如何使用 matplotlib 库来绘制包含折线图和条形图的复合图。 效果 代码 imp…...

云计算中网络虚拟化的核心组件——NFV、NFVO、VIM与VNF
NFV NFV(Network Functions Virtualization,网络功能虚拟化),是一种将传统电信网络中的网络节点设备功能从专用硬件中解耦并转换为软件实体的技术。通过运用虚拟化技术,NFV允许网络功能如路由器、防火墙、负载均衡器、…...

# SpringBoot 如何让指定的Bean先加载
SpringBoot 如何让指定的Bean先加载 文章目录 SpringBoot 如何让指定的Bean先加载ApplicationContextInitializer使用启动入口出注册配置文件中配置spring.factories中配置 BeanDefinitionRegistryPostProcessor使用 使用DependsOn注解实现SmartInitializingSingleton接口使用P…...

家用洗地机哪个品牌好?洗地机怎么选?这几款全网好评如潮
如今,人们家里越来越多的智能清洁家电,小到吸尘器、电动拖把,大到扫地机器人、洗地机,作为一个用过所有这些清洁工具的家庭主妇,我觉得最好用的还是洗地机。它的清洁效果比扫地机器人更好,功能也比吸尘器更…...

iOS与前端:深入解析两者之间的区别与联系
iOS与前端:深入解析两者之间的区别与联系 在数字科技高速发展的今天,iOS与前端技术作为两大热门领域,各自在移动应用与网页开发中扮演着不可或缺的角色。然而,这两者之间究竟存在哪些差异与联系呢?本文将从四个方面、…...
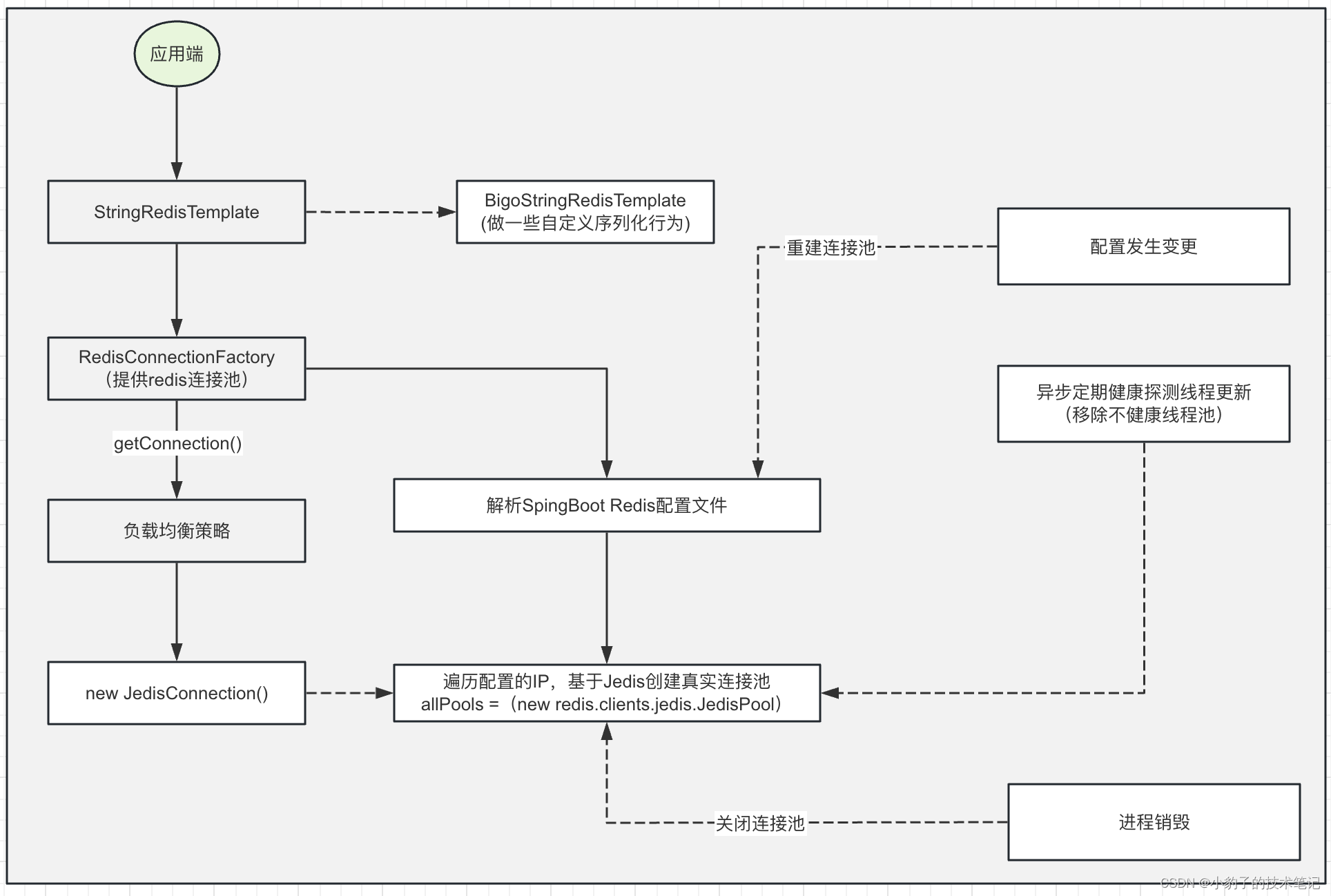
SpringBoot 基于jedis实现Codis高可用访问
codis与redis的关系 codis与redis之间关系就是codis是基于多个redis实例做了一层路由层来进行数据的路由,每个redis实例承担一定的数据分片。 codis作为开源产品,可以很直观的展示出codis运维成本低,扩容平滑最核心的优势. 其中࿰…...

力扣108. 将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树 - 力扣(LeetCode) 找割点,一步一步将原数组分开。妙极了!!!!! /*** Definition for a binary tree node.* public class TreeNode {* int val;…...
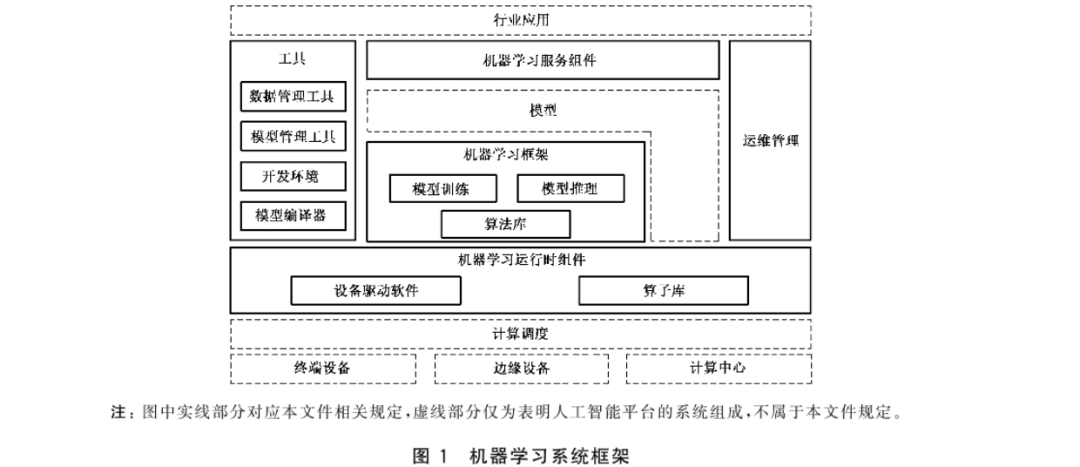
人工智能机器学习系统技术要求
一 术语和定义 1.1机器学习系统 machinelearningsystem 能运行或用于开发机器学习模型、算法和相关应用的软件系统。 1.2机器学习框架 machinelearningframework 利用预先构建和优化好的组件集合定义模型,实现对机器学习算法封装、数据调用处理和计算资源使用的软件库。 1…...

学习整理使用JavaScript中如何判断变量是否存在的四种常用方法
学习整理使用JavaScript中如何判断变量是否存在的四种常用方法 前言1. 使用 typeof 运算符判断变量类型2. 使用全局对象 window 或 global 判断变量是否存在3. 使用 in 关键字判断变量是否存在4. 使用 try…catch 块判断变量是否存在5. 综合示例总结 前言 在 JavaScript 中&am…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
