代码随想录算法训练营第四十四天 | 01背包问题理论基础、01背包问题滚动数组、416. 分割等和子集
背包问题其实有很多种,01背包是最基础也是最经典的,软工计科学生一定要掌握的。

01背包问题
代码随想录
视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili
思路
直接上动态规划五部曲
1、dp数组及其下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
2.确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3.初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
再看其他情况。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
4.确定遍历顺序
在如下图中,可以看出,有两个遍历的维度:物品与背包重量
那么问题来了,先遍历 物品还是先遍历背包重量呢?
其实都可以!! 但是先遍历物品更好理解。
5.举例验证,直接看链接里的吧。
代码
def test_2_wei_bag_problem1():weight = [1, 3, 4]value = [15, 20, 30]bagweight = 4# 二维数组dp = [[0] * (bagweight + 1) for _ in range(len(weight))]# 初始化for j in range(weight[0], bagweight + 1):dp[0][j] = value[0]# weight数组的大小就是物品个数for i in range(1, len(weight)): # 遍历物品for j in range(bagweight + 1): # 遍历背包容量if j < weight[i]:dp[i][j] = dp[i - 1][j]else:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])print(dp[len(weight) - 1][bagweight])test_2_wei_bag_problem1()
01背包滚动数组
代码随想录
视频讲解:带你学透01背包问题(滚动数组篇) | 从此对背包问题不再迷茫!_哔哩哔哩_bilibili
看链接吧,老是复制粘贴累了。
416.分割等和子集
本题是 01背包的应用类题目代码随想录
视频讲解:动态规划之背包问题,这个包能装满吗?| LeetCode:416.分割等和子集_哔哩哔哩_bilibili
思路
就是01背包的应用,背包的大小是总和的一半,遍历每一个物品,看看遍历到最后能不能装满这个背包。
代码(二维版本在链接里)
class Solution:def canPartition(self, nums: List[int]) -> bool:if sum(nums) % 2 != 0:return Falsetarget = sum(nums) // 2dp = [0] * (target + 1)for num in nums:for j in range(target, num-1, -1):dp[j] = max(dp[j], dp[j-num] + num)return dp[-1] == target相关文章:

代码随想录算法训练营第四十四天 | 01背包问题理论基础、01背包问题滚动数组、416. 分割等和子集
背包问题其实有很多种,01背包是最基础也是最经典的,软工计科学生一定要掌握的。 01背包问题 代码随想录 视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经…...

【PingPong_注册安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞 …...
车辆路径规划之Dubins曲线与RS曲线简述
描述 Dubins和RS曲线都是路径规划的经典算法,其中车辆运动学利用RS曲线居多,因此简单介绍Dubins并引出RS曲线。 花了点时间看了二者的论文,并阅读了一个开源的代码。 Dubins曲线 Dubins曲线是在满足曲率约束和规定的始端和末端的切线&#…...

PostgreSQL 和Oracle锁机制对比
PostgreSQL 和Oracle锁机制对比 PostgreSQL 和 Oracle 都是业界广泛使用的关系型数据库管理系统,它们在锁机制方面都有独到的设计来控制并发访问,确保数据的一致性和完整性。下面我们详细比较一下这两个数据库系统的锁机制。 1. 锁类型 PostgreSQL P…...

6月05日,每日信息差
第一、特斯拉在碳博会上展示了其全品类的可持续能源解决方案,包括首次在国内展出的超大型电化学商用储能系统 Megapack 和家庭储能系统 Powerwall。此外,特斯拉还展示了电动汽车三电系统的解构和电池回收技术产品 第二、2024 年第一季度,全球…...

MongoDB~俩大特点管道聚合和数据压缩(snappy)
场景 在MySQL中,通常会涉及多个表的一些操作,MongoDB也类似,有时需要将多个文档甚至是多个集合汇总到一起计算分析(比如求和、取最大值)并返回计算后的结果,这个过程被称为 聚合操作 。 根据官方文档介绍&…...

HTML+CSS+JS 动态登录表单
效果演示 实现了一个登录表单的背景动画效果,包括一个渐变背景、一个输入框和一个登录按钮。背景动画由多个不同大小和颜色的正方形组成,它们在页面上以不同的速度和方向移动。当用户成功登录后,标题会向上移动,表单会消失。 Code <!DOCTYPE html> <html lang=&q…...

统一返回响应
前言 我们为什么要设置统一返回响应 提高代码的可维护性:通过统一返回请求的格式,可以使代码更加清晰和易于维护,减少重复的代码,提高代码质量。 便于调试和测试:统一的返回格式使得在调试和测试时更为简单ÿ…...
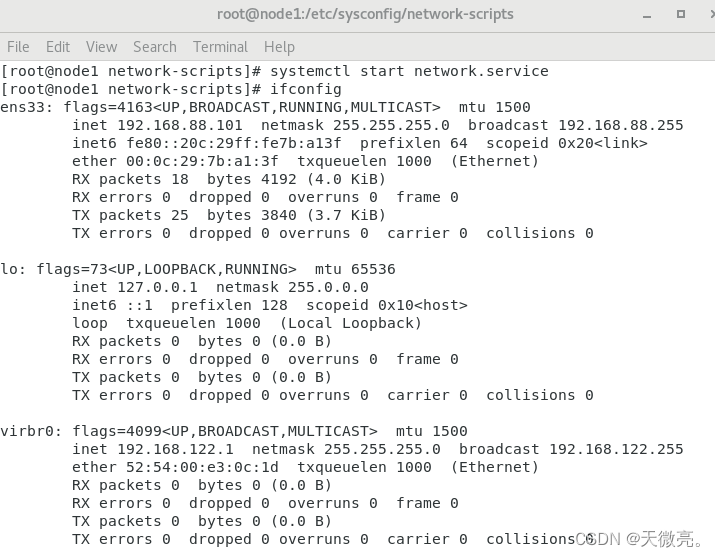
大数据学习问题记录
问题记录 node1突然无法连接finalshell node1突然无法连接finalshell 今天我打开虚拟机和finalshell的时候,发现我的node1连接不上finalshell,但是node2、node3依旧可以链接,我在网上找了很多方法,但是是关于全部虚拟机连接不上finalshell&a…...
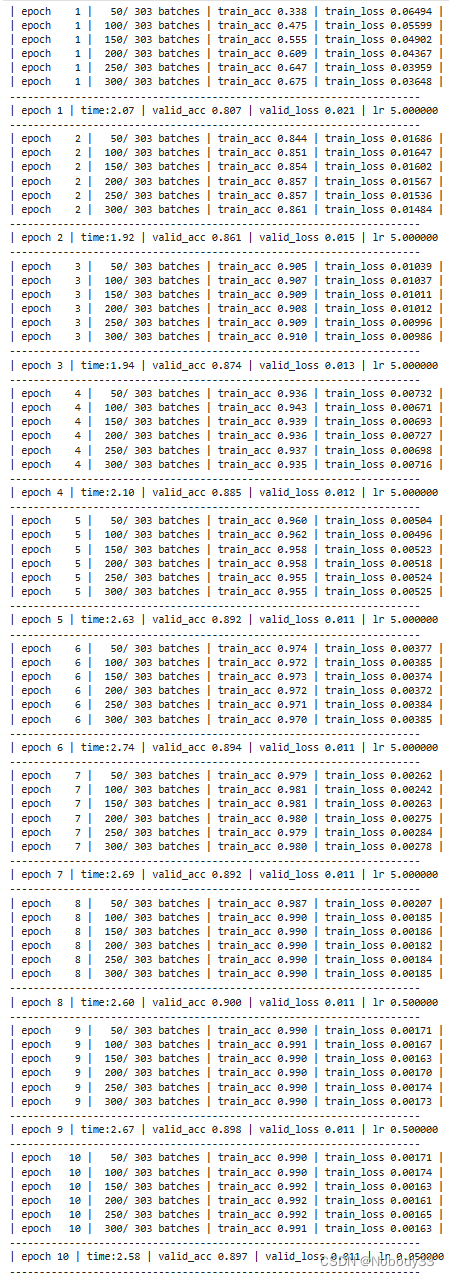
第N4周:中文文本分类
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 一、预备知识 中文文本分类和英文文本分类都是文本分类,为什么要单独拎出来个中文文本分类呢? 在自然语言处理(NLP&#x…...
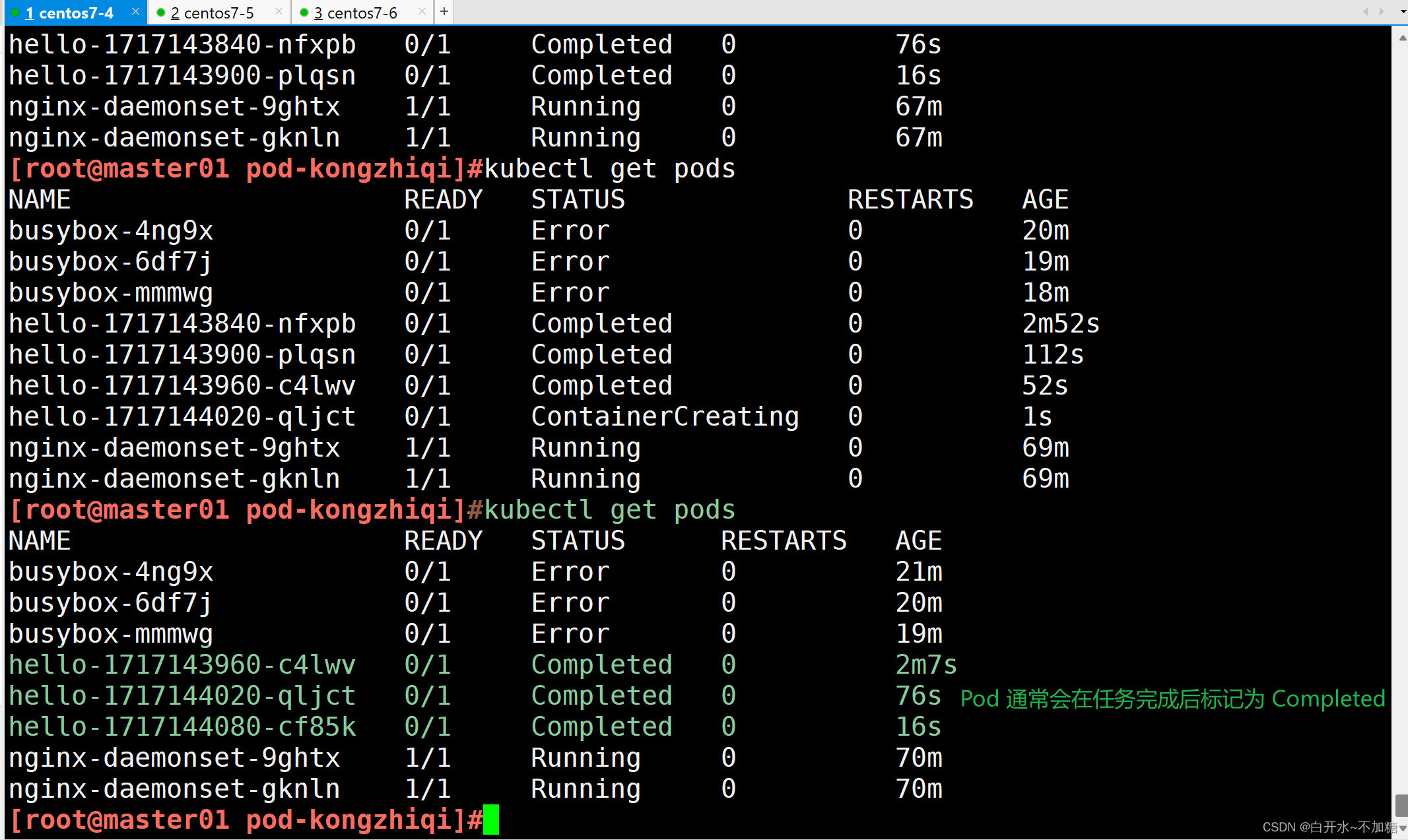
【kubernetes】探索k8s集群的pod控制器详解(Deployment、StatefulSet、DaemonSet、Job、CronJob)
目录 一、Pod控制器及其功用 二、pod控制器有多种类型 2.1ReplicaSet 2.1.1ReplicaSet主要三个组件组成 2.2Deployment 2.3DaemonSet 2.4StatefulSet 2.5Job 2.6Cronjob 三、Pod与控制器之间的关系 3.1Deployment 3.2SatefulSet 3.2.1StatefulSet三个组件 3.2.2为…...

直接插入排序
#include <stdio.h>void insert_sort(int arr[], int n) {int i;int j;int tmp;for (i 1; i < n; i){tmp arr[i];j i - 1;// 将要插入的元素与数组中的元素比较(从后向前比) while (j > 0 && arr[j] > tmp){arr[j 1] arr[…...

esp32s3 nvs 存储过程中使用malloc和free函数的一点困惑
我的项目中,大量使用了malloc()和free()函数,在使用nvs存储之前没有出现问题。 esp32厂家nvs的blob存储的例程中,有使用malloc()和free(),我参照例程写了自己的blob存储函数f,一开始是可以正常使用的,后来…...

除visio以外的几款好用流程图绘制工具
流程图绘制软件在嵌入式软件开发中扮演着重要的角色,它们能够帮助用户清晰、直观地展示工作流程。以下是几款流行的流程图绘制软件及其特点的详细报告: 思维导图MindMaster MindMaster作为一款专业的思维导图软件,不仅具备强大的思维导图制作…...

CentOS 7 64位 常用命令
一、系统管理命令 systemctl start firewalld.service:启动防火墙服务 systemctl stop firewalld.service:停止防火墙服务 systemctl enable firewalld.service:设置防火墙服务开机自启 systemctl disable firewalld.service:禁止…...

ChatGPT-4o抢先体验
速度很快,结果很智能,支持多模态输入输出,感兴趣联系作者。 windows/linux/mac 客户端下载参考:https://github.com/lencx/Noi...

STM32实验之USART串口发送+接受数据(二进制/HEX/文本)
涉及三个实验: 1.USART串口发送和接收数据 我们使用的是将串口封装成为一个Serial.c模块.其中包含了 void Serial_Init(void);//串口初始化 void Serial_SendByte(uint8_t Byte);//串口发送一个字节 void Serial_SendArray(uint8_t *Array,uint16_t Length);//…...

网关(Gateway)- 内置过滤器工厂
官方文档:Spring Cloud Gateway 内置过滤器工厂 AddRequestHeaderGatewayFilterFactory 为请求添加Header Header的名称及值 配置说明 server:port: 8088 spring:application:name: api-gatewaycloud:nacos:discovery:server-addr: 127.0.0.1:8847username: nacos…...
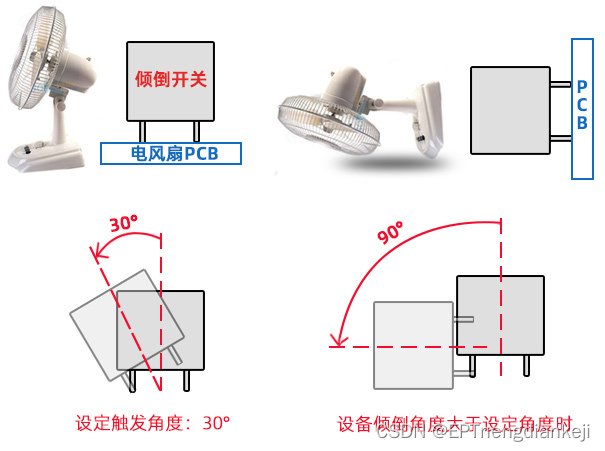
电风扇如何实现跌倒断电保护功能
电风扇作为日常生活中常用的家电产品,为了提升安全性能,在设计上通常会考虑加入跌倒断电保护功能。其中,光电倾倒开关是实现跌倒断电保护功能的关键组件之一。 光电倾倒开关内置红外发光二极管和光敏接收器,其工作原理非常巧妙。…...

编译原理总结
编译器构成 1. 前端分析部分 1.1 词法分析 确定词性,输出为token序列 1.2 语法分析 识别短语 1.3 语义分析 分析短语在句子中的成分 IR中间代码生成 2. 机器无关代码优化 3. 后端综合部分 目标代码生成 机器相关代码优化 4. 其他 全局信息表 异常输出...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
