基于R语言BIOMOD2 及机器学习方法的物种分布模拟与案例分析实践技术
BIOMOD2是一个R软件包,用于构建和评估物种分布模型(SDMs)。它集成了多种统计和机器学习方法,如GLM、GAM、SVM等,允许用户预测和分析物种在不同环境条件下的地理分布。通过这种方式,BIOMOD帮助研究者评估气候变化、生境丧失等因素对生物多样性的潜在影响。
【目标】:
1、理解物种分布模型的基本原理:理解物种分布模型(SDMs)的理论基础,包括模型的种类、用途以及在生态研究和环境管理中的应用。
2、BIOMOD2软件包的使用:在R环境中有效地使用BIOMOD2软件包,包括数据准备、模型构建、模型评估和结果解释。
3、提高数据分析和处理能力:获取、处理和分析环境与物种数据的能力,包括数据清洗、变量选择和模型优化。
4、应用模型解决实际问题:通过案例和实际操作,将所学知识应用于解决真实世界的问题,如生物多样性保护、气候变化影响评估和入侵物种管理。
【内容简介】 :
一、引入和理论基础
课程介绍:目标、流程和期望成果。
生态模型基础:介绍生态模型的基本概念和物种分布模型(SDMs)的重要性。
biomod2简介:探讨biomod2的历史、发展和主要功能。
R语言重点工具入门:数据输入与输出、科学计算、地理数据分析、数据可视化等功能。
二、数据获取与预处理
常见地球科学数据讲解(数据特点与获取途径):
(1)物种分布数据;
(2)环境变量(站点数据、遥感数据)。
基于R语言的数据预处理:
- 数据提取:根据需求批量提取相关数据;
- 数据清洗:数据清洗的原则与方法;
- 特征变量选择: 通过相关性分析、主成分分析(PCA)等方法选择具有代表性的特征变量,提高模型效率。
第三、模型的建立与评估
机器学习概述与R语言实践
(1)机器学习原理;(2)常见机器学习算法与流程
基于单一机器学习算法的物种分布特征模拟(以最大熵算法为例)。
biomod2程序包介绍与使用:原理、构成
实际操作:构建第一个物种分布模型,包括选择模型类型和调整参数。
模型评估方法:通过ROC曲线、AUC值等方法评估模型的有效性和准确性。
第四、模型优化与多模型集成
典型算法参数优化:对随机森林、最大熵等算法进行参数优化,提高模型性能。
集成方法:结合多个模型提高预测结果的稳定性和准确性。
物种分布特征预测: 基于单一模型与集成模型预测物种未来分布特征。
实战演练:参与者使用自己的数据或示例数据集,尝试实现多模型集成
第五、结果分析和案例研究
种分布特征、环境变量与物种分布关系、未来分布特征预测。
科学制图:栅格图、柱状图、降维结果图等。
案例研究:分析物种分布案例,如何应用学到的技能和知识。
总结:回顾学习要点,讨论如何将这些技能应用到未来的研究中。
相关文章:

基于R语言BIOMOD2 及机器学习方法的物种分布模拟与案例分析实践技术
BIOMOD2是一个R软件包,用于构建和评估物种分布模型(SDMs)。它集成了多种统计和机器学习方法,如GLM、GAM、SVM等,允许用户预测和分析物种在不同环境条件下的地理分布。通过这种方式,BIOMOD帮助研究者评估气候…...

Objective-C之通过协议提供匿名对象
概述 通过协议提供匿名对象的设计模式,遵循了面向对象设计的多项重要原则: 接口隔离原则:通过定义细粒度的协议来避免实现庞大的接口。依赖倒置原则:高层模块依赖于抽象协议,而不是具体实现。里氏替换原则࿱…...

C语言基础(一)
C语言基础 一、标准输出(格式化输出):1、概念:2、注意语法点:3、格式控制符:4、调试技巧:5、代码风格:6、实例: 二、数据类型:1、整型概念:语法&a…...

机器学习_决策树与随机森林
决策树是一种常用的监督学习算法,既可以用于分类任务也可以用于回归任务。决策树通过递归地将数据集划分成更小的子集,逐步建立树结构。每个节点对应一个特征,树的叶子节点表示最终的预测结果。构建决策树的关键是选择最佳的特征来分割数据&a…...

嵌入式系统日志轮转:实现与性能考量
日志轮转是嵌入式系统中管理日志文件的一种常用技术,它通过创建新的日志文件来替代旧的日志文件,从而避免日志文件无限增长,占用过多存储空间。本文将探讨日志轮转的实现方法以及在嵌入式系统中实现日志轮转时需要考虑的性能因素。 一、日志…...

麦肯锡:ChatGPT等生成式AI应用激增,大中华区增长最快
全球顶级咨询公司麦肯锡(McKinsey & Company)在官网发布了《he state of AI in early 2024:Gen AI adoption spikes and starts to generate value》,一份关于生成式AI应用的调查报告。 麦肯锡对多个国家/地区的1,363位管理者进行了调查…...

Vue Router 使用教程
Vue Router 是 Vue.js 的官方路由管理器,它提供了一种方便的方式来管理应用的路由。在本教程中,我们将介绍 Vue Router 的一些常见用法和示例。 一、安装 Vue Router 使用 Vue Router 之前,需要先安装它。可以使用以下命令通过 npm 安装&am…...

银河麒麟解压命令
银河麒麟(Kylin)操作系统是基于Linux的操作系统分支之一,其使用的解压命令与Linux系统中的命令基本相同。 在银河麒麟系统中,常用的解压命令有以下几种: 对于.tar文件: tar -xvf file.tar对于.tar.gz或.…...

VSCode打开文件总是在当前标签页打开,不是新增标签页
修改 VS Code 设置 打开设置: 按 Ctrl , 或者点击右下角的齿轮图标,然后选择 “Settings”。 搜索设置: 在设置搜索栏中输入 workbench.editor.enablePreview。 禁用预览模式: 找到 Workbench > Editor: Enable Preview 选…...

Django redirect()函数实现页面重定向
1,通过路由反向解析进行重定向 1.1 添加视图函数 myshop/app2/views.py from django.http import HttpResponse from django.shortcuts import render from django.urls import reverse def index(request):return HttpResponse("app2 的index")# 反向…...

【运维项目经历|029】NTP精准时间同步系统优化项目
🍁博主简介: 🏅云计算领域优质创作者 🏅2022年CSDN新星计划python赛道第一名 🏅2022年CSDN原力计划优质作者 🏅阿里云ACE认证高级工程师 🏅阿里云开发者社区专家博主 💊交流社区:CSDN云计算交流社区欢迎您的加入! 目...

机房网络运维服务项目难点与关键点分析
随着信息技术的飞速发展,机房作为支撑企业信息化建设的核心枢纽,其网络运维服务的重要性日益凸显。然而,在实际运维过程中,运维团队常常面临诸多难点和挑战。本文将围绕机房网络运维服务项目的难点和关键点进行深入分析࿰…...

MKS AX7680 SERIES 电源使用说明手侧
MKS AX7680 SERIES 电源使用说明手侧...
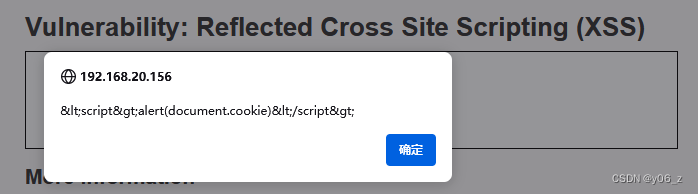
DVWA-XSS(Reflected)
反射型XSS可以用来窃取cookie Low 输入1111进行测试,发现1111被打印 输入<script>alert(document.cookie)</script>,出现弹窗,获得cookie Medium 查看后端代码,发现对<script>进行了转义,但是…...
Python自动化办公2.0 即将发布
第一节课:数据整理与清洗 第二节课:数据筛选、过滤与排序 第三节课:高级数据处理技巧 第四节课:数据可视化与实践案例 第五节课:统计分析与报表 第六节:常见的Excel报表 与下方的课程形成知识体系&…...

【面试宝藏】Redis 常见面试题解析其二
Redis 高级面试题解析 20. 说说 Redis 哈希槽的机制? Redis 集群采用哈希槽(Hash Slot)机制来分布和管理数据。整个哈希空间被划分为 16384 个槽,每个键通过 CRC16 校验后取模映射到一个哈希槽。每个节点负责一部分哈希槽&#…...

智慧公厕厂家+智能厕所小程序,构建数字化公厕新体系
在现代社会的诸多场景中,公厕扮演着重要却常常被忽视的角色。尤其是在传统的楼宇中,公厕存在着一系列痛点问题。 一、传统公厕问题 传统楼宇公厕常常面临着布局不合理的困境,导致使用者寻找困难,浪费时间和精力。卫生状况也是一大…...
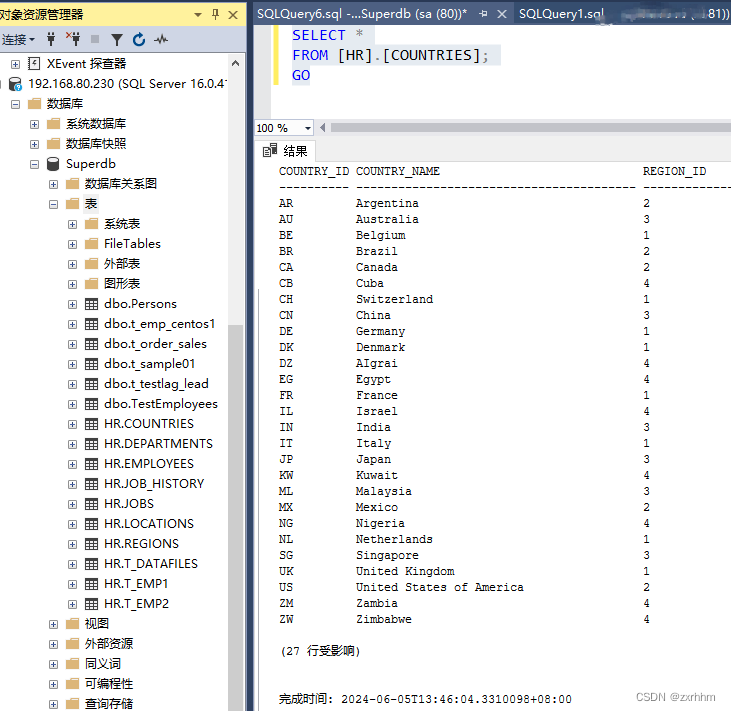
使用迁移助手 (SSMA for Oracle) 将Oracle19c数据库迁移到SQL Server2022
如何使用适用于 Oracle 的 SQL Server 迁移助手Microsoft SQL Server Migration Assistant for Oracle (SSMA for Oracle) 将 Oracle 数据库迁移到 SQL Server Microsoft SQL Server Migration Assistant (SSMA) for Oracle is a tool to automate migration from Oracle data…...

LabVIEW开发EOL功能测试系统
LabVIEW开发EOL功能测试系统 介绍了一种基于LabVIEW开发的EOL功能测试系统方案,涵盖软件架构、工作流程、模块化设计、低耦合性、易于修改与维护、稳定性及硬件选型。系统通过高效的CAN通信实现对电机控制器的全面测试,确保运行可靠并支持未来的升级需求…...

Java finally catch try关键字
Java finally catch try关键字 finally: finally 关键字用来创建在 try 代码块后面执行的代码块;无论是否发生异常,finally 代码块中的代码总会被执行。 在 finally 代码块中,可以进行文件流关闭等收尾善后性质的语句 catch&am…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...
