数据结构 | 超详细讲解七大排序(C语言实现,含动图,多方法!)
目录
编辑
排序的概念
常见排序算法
编辑
1.冒泡排序
🍹图解
🥳代码实现
🤔时间复杂度
2.插入排序
🍹图解
🌴深度剖析
🍎代码思路
🥳代码实现
🤔时间复杂度
3.希尔排序
🌴深度剖析
🍎代码思路
🍋思考:关于gap的取值问题
🥳代码实现
🤔时间复杂度
4.堆排序
⛱️请看我的另一篇文章:详解堆排序
5.选择排序
🍹图解
🌴深度剖析
🥳代码实现
🤔时间复杂度
6.快速排序
🍹图解1:霍尔法
🌴深度剖析
🍎代码思路
🍎优化1:改变选key策略,采用三数选中法
🍎优化2:小区间优化,采用其它排序方法,减少递归次数
🍋思考:如何保证相遇位置比key小?
🥳代码实现
🍹图解2:前后指针法
🌴深度剖析
🍎代码思路
🍎优化:避免自己和自己交换
🥳代码实现
🍹非递归实现
🍎代码思路
🥳代码实现
7.归并排序
🍹图解
🌴深度剖析
🍹递归版
🍎代码思路
🥳代码实现
🍹非递归版
🍎代码思路
🍋思考:上面的思路只能解决数组大小为的数组,其余数组则会存在越界问题,如何解决?
🥳代码实现
🤔时间复杂度
排序的概念
排序 :所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。稳定性 :假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中, r[i]=r[j] ,且 r[i] 在 r[j] 之前,而在排序后的序列中, r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。内部排序 :数据元素全部放在内存中的排序。外部排序 :数据元素太多不能同时放在内存中,根据排序过程的要求不断地在内外存之间移动数据的排序。
常见排序算法
下文将会细细介绍上图中七种排序,观看前,可以点一个免费的赞与收藏支持作者~希望本篇博客能帮助到你!
1.冒泡排序
相邻两个数进行比较,大的数向后移,每次循环都能冒出一个大的数到数组最后,直至最后全部冒出。
🍹图解
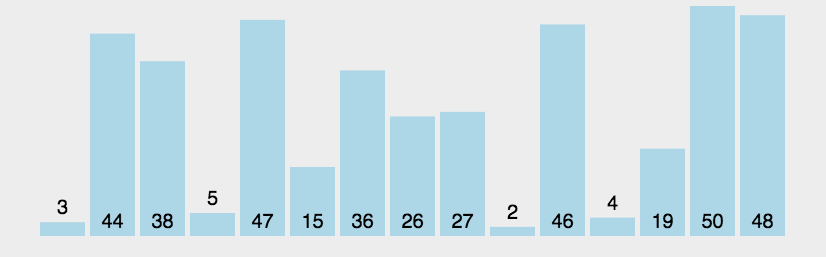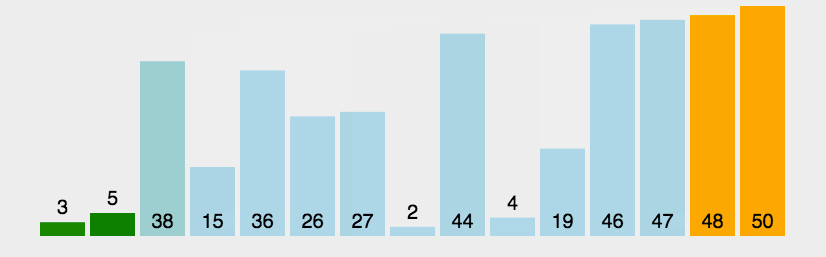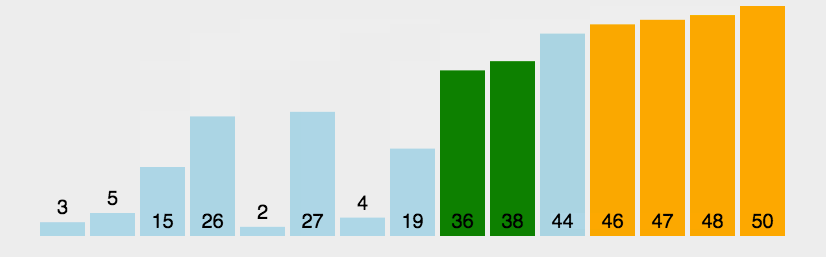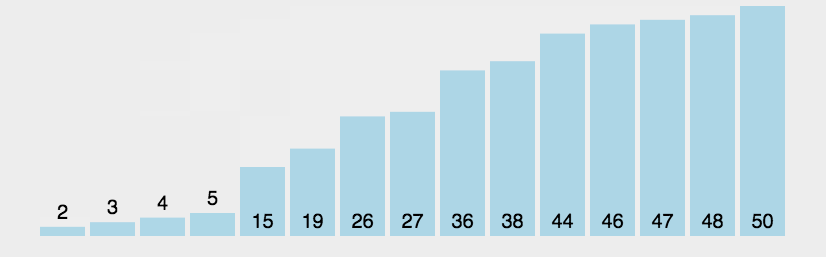
🥳代码实现
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>void bubble_sort(int arr[],int sz)
{int flag = 1;//优化int i = 0;for (i = 0; i < sz - 1; i++) {int j = 0;for (j = 0; j < sz - 1 - i; j++) {if (arr[j] > arr[j + 1]) {flag = 0;int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;}}if (flag == 1) {break;}}
}int main() {int n = 0;int arr[] = {2,6,9,3,6,9,1};int sz = sizeof(arr) / sizeof(arr[0]);bubble_sort(arr, sz);for (n = 0; n < sz - 1; n++) {printf("%d", arr[n]);}return 0;
}🤔时间复杂度
O(N^2)
2.插入排序
🍹图解
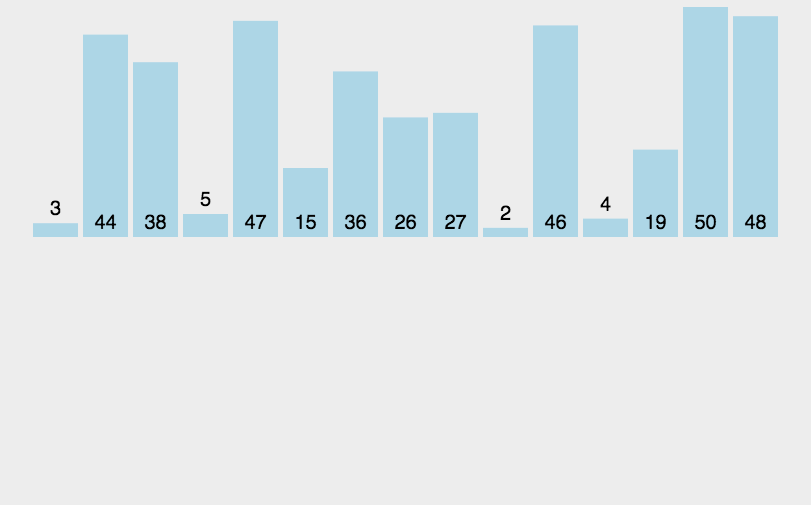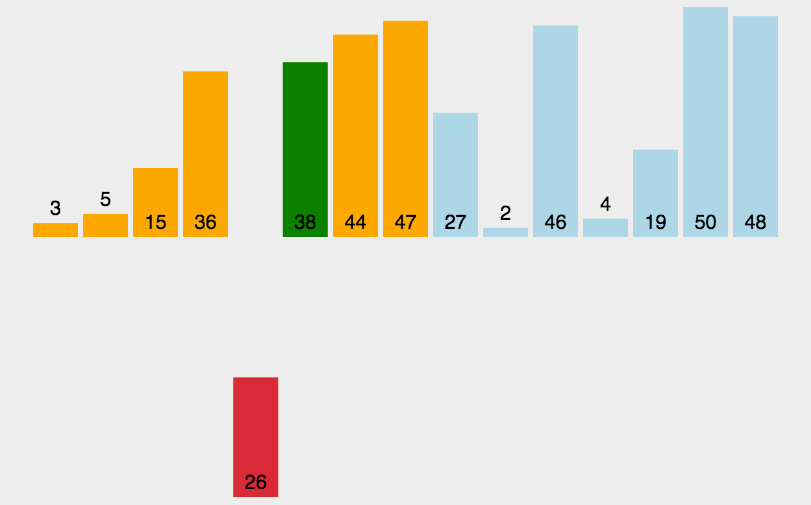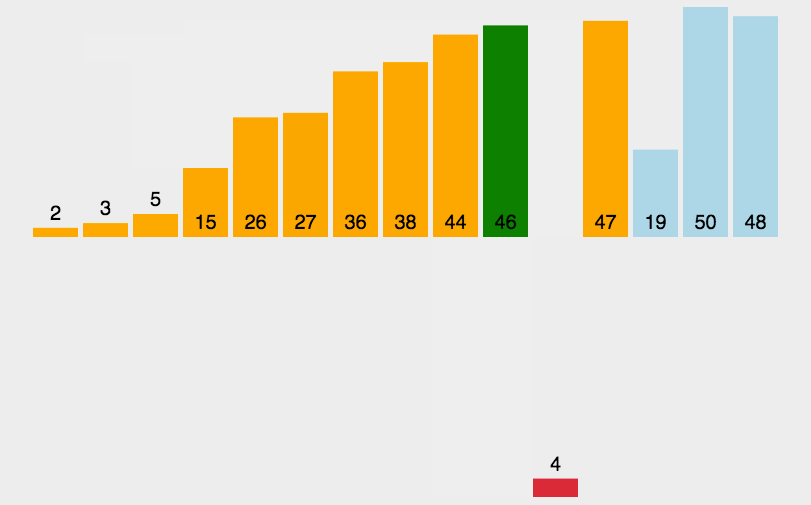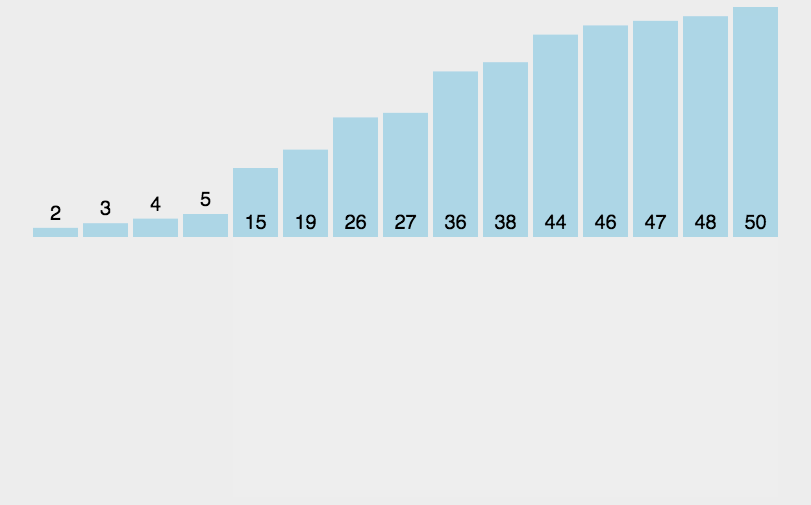
🌴深度剖析
🍎代码思路
上图为基本的插入排序,可对其进行优化:依次遍历找出最大值和最小值索引。
代码思路:1.设变量mini,maxi分别为最小值和最大值索引
设begin,end分别无序部分的首尾索引。
2.遍历无序部分,找出最小值和最大值的索引mini,maxi
3.将a[begin]和a[mini]进行交换,将a[end]和a[maxi]进行交换
注意:两次交换的中间需要进行依次判断,判断maxi是否仍然等于begin,因为经过第一个交换后原begin位置的值已经交换到mini位置去了,如果判断成立,maxi也应该跟随原begin的值的移动移动到mini位置。
4.此时begin、end处已经属于有序部分,begin++,end--,,更新无序部分的范围。
5.对剩余无序部分重复上述步骤,直到begin==end。
🥳代码实现
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}void selectsort(int* a, int n) {int begin = 0;int end = n - 1;while (begin < end) {int mini = begin;int maxi = begin;//找最大值最小值的索引for (int i = begin + 1; i <= end; i++) {if (a[i] < a[mini]) {mini = i;}if (a[i] > a[maxi]) {maxi = i;}}//进行交换swap(&a[mini], &a[begin]);if (maxi == begin)//begin此时被mini换走了maxi = mini;swap(&a[maxi], &a[end]);begin++;end--;}}int main() {int a1[8] = { 9,1,2,5,7,4,6,3};selectsort(a1,8);//int a2[5] = { 3,2,5,6,7 };//selectsort(a2, 5);for (int i = 0; i < 8; i++) {printf("%d ", a1[i]);}return 0;
}🤔时间复杂度
O(N^2)
3.希尔排序
🌴深度剖析
🍎代码思路
希尔排序是在插入排序的基础上进行优化的。
1.预排序:将数组分为gap组,进行预排序(让数组接近有序)
2.插入排序(此时,数组近乎有序,使用插入排序效率极高)
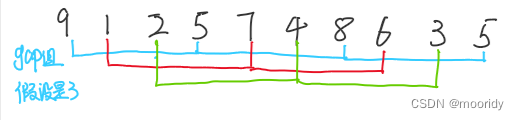
即蓝色的为一组,红色的为一组,绿色为一组,对每组进行插入排序
以下是预排序的代码:
//预排序过程,假设gap=3
//第一种写法:依次对三组进行预排序
for(int j=0;j<gap;j++){ //依次对三组进行预排序
for (int i = gap; i < n; i+=gap) { //对一组进行预排序的过程,由于一组内部元素之间相距gap,所以应该是i+=gapint end = i;int tmp = a[end];while (end >= gap) {if (tmp < a[end - gap]) {a[end] = a[end - gap];a[end - gap] = tmp;end -= gap;}else {break;}} }
//第二种写法:同时进行三组的预排序(但效率相较上一种写法其实没有改变)
for (int i = gap; i < n; i++) {//先对蓝组排1下,再对红组排1下,再对绿组排1下,如此循环int end = i;int tmp = a[end];while (end >= gap) {if (tmp < a[end - gap]) {a[end] = a[end - gap];a[end - gap] = tmp;end -= gap;}else {break;}}🍋思考:关于gap的取值问题
gap越大:大的数字越快跳到后面,小的数字越快跳到前面,结果越不接近有序。
gap越小:跳得越慢,但结果越接近有序(gap==1时,相当于插入排序)
解决方案:走多组gap,gap>1时就是预排序
gap==1时就是插入排序
gap我们通常设置为gap=gap/3+1
这里+1是为了保证gap>=1。
🥳代码实现
//1.预排序,分成gap组进行//2.插入排序void ShellSort(int* a, int n) {int gap = n;while (gap>1) {gap = gap / 3 + 1;//保证gap>=1for (int i = gap; i < n; i++) {int end = i;int tmp = a[end];while (end >= gap) {if (tmp < a[end - gap]) {a[end] = a[end - gap];a[end - gap] = tmp;end -= gap;}else {break;}}}}}🤔时间复杂度
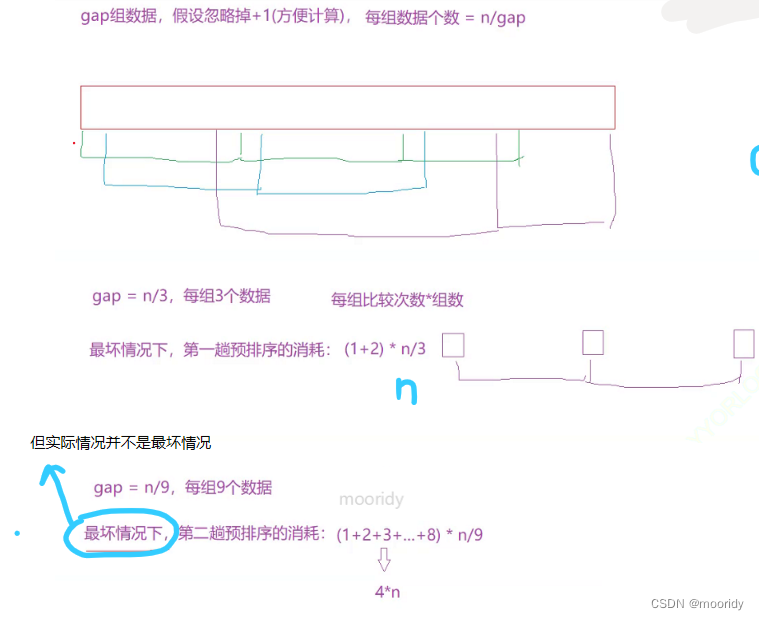
4.堆排序
⛱️
请看我的另一篇文章:详解堆排序
5.选择排序
🍹图解
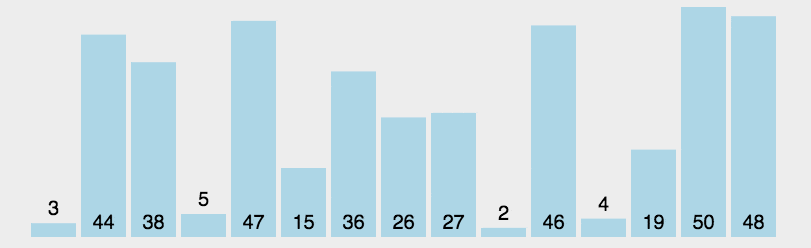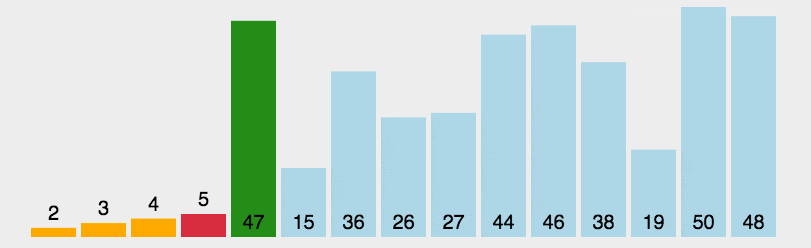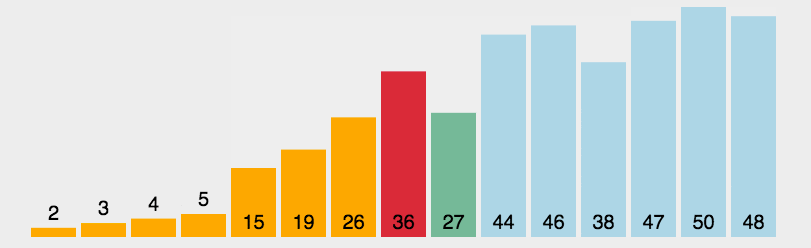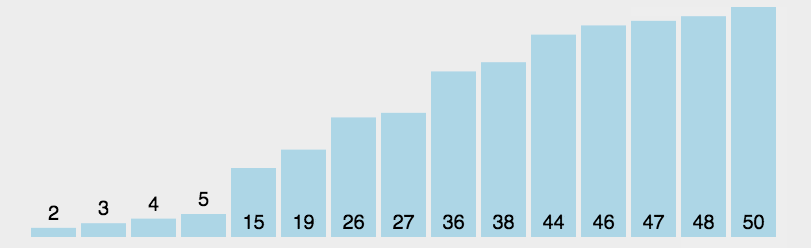
🌴深度剖析
基本思路:遍历一遍,选择最小的插到最左边
优化思路:遍历一遍,选出最小的最大的分别插到最左最右
一个小坑:将最大值放到最后后,可能破坏了原本的
🥳代码实现
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}void selectsort(int* a, int n) {int begin = 0;int end = n-1 ;while (begin < end) {int mini = a[begin];int maxi = a[end];for (int i = begin; i <= end; i++) {if (a[i] < mini) {mini = a[i];swap(&a[i], &a[begin]);}if(a[i]>maxi) {maxi = a[i];swap(&a[i], &a[end]);}//验证if (a[i] <= mini) {mini = a[i];swap(&a[i], &a[begin]);}}begin++;end--;}}int main() {int a1[8] = { 9,1,2,5,7,4,6,3};selectsort(a1,8);//int a2[5] = { 3,2,5,6,7 };//selectsort(a2, 5);for (int i = 0; i < 8; i++) {printf("%d ", a1[i]);}return 0;
}🤔时间复杂度
O(N^2)
6.快速排序
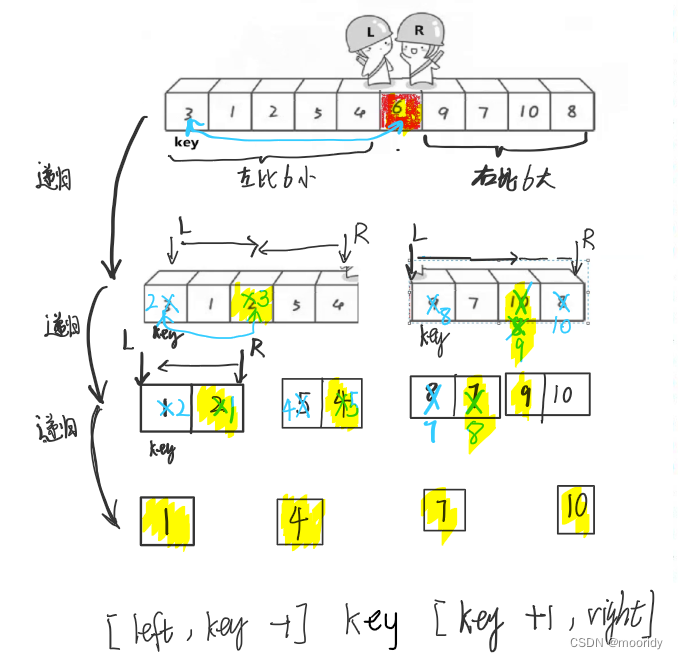
🍹图解1:霍尔法
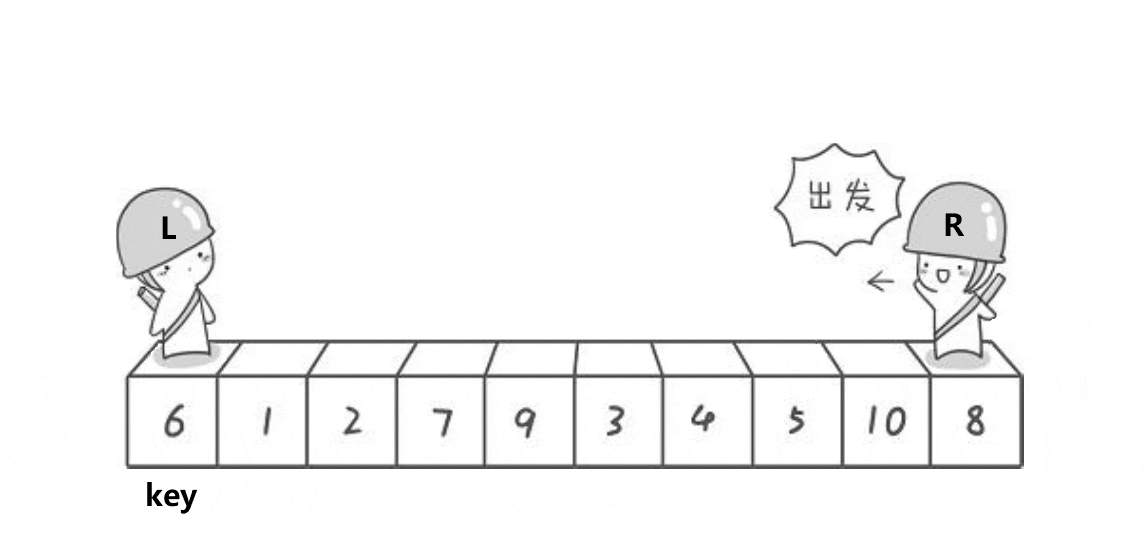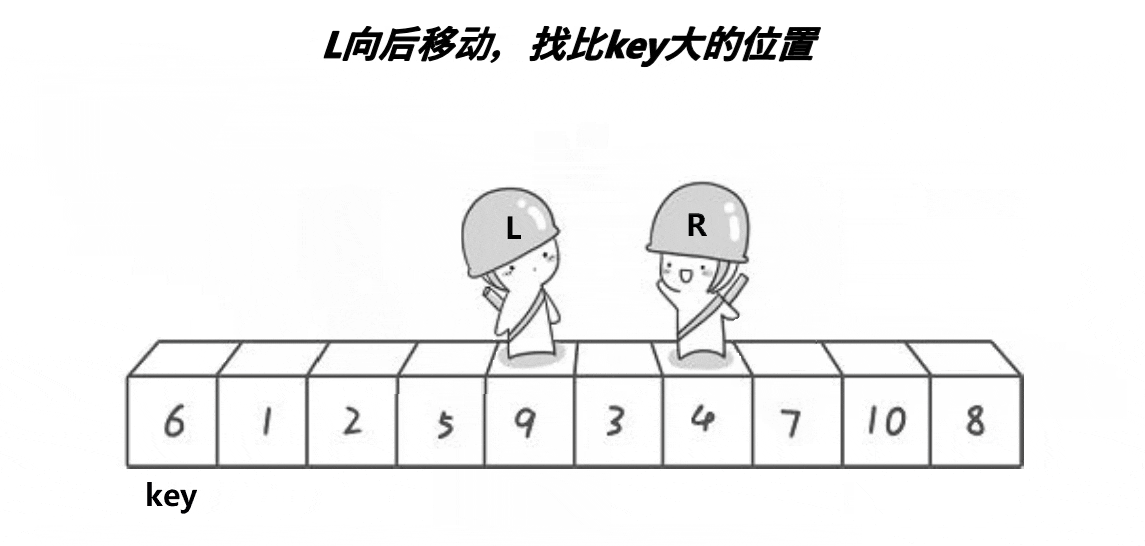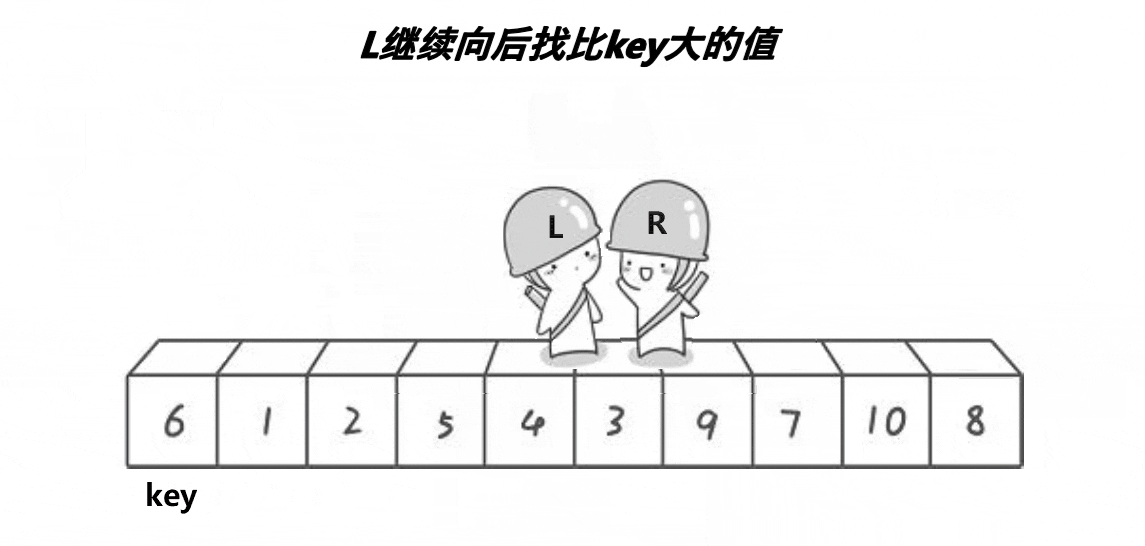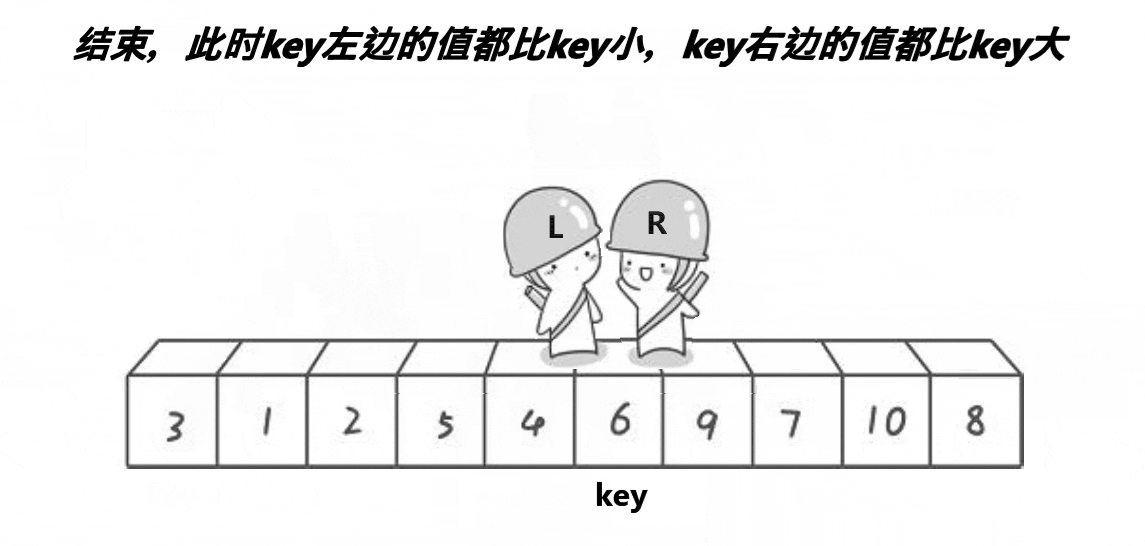
🌴深度剖析
🍎代码思路
我们先考虑单趟:
end,begin相遇前:end向前走找比key小的值,begin向后走找比key大的值,都找到后两者进行交换
end,begin相遇时:循环停止,交换begin和key
单趟过后的结果:
key所在位置一定是正确的位置,[left,key-1]中的值一定小于key,[key+1,right]中的值一定大于key
//单趟(一定先走end,再走begin)
int begin = left;int end = right;int key = left;while (begin < end) {while (a[end] >= a[key] && begin < end) {end--;}while(a[begin] <= a[key]&&begin<end) {begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[key]);
key = begin;此时整个数组可以划分为三个部分:[left,key-1],key, [key+1,right]
递归:接着就用递归思想对[left,key-1],[key+1,right]中的值进行排序
递归结束条件:数组不存在或者只有1个元素
🍎优化1:改变选key策略,采用三数选中法
当数组有序排列时,且数据量较大时,基础版快排可能出现栈溢出问题。
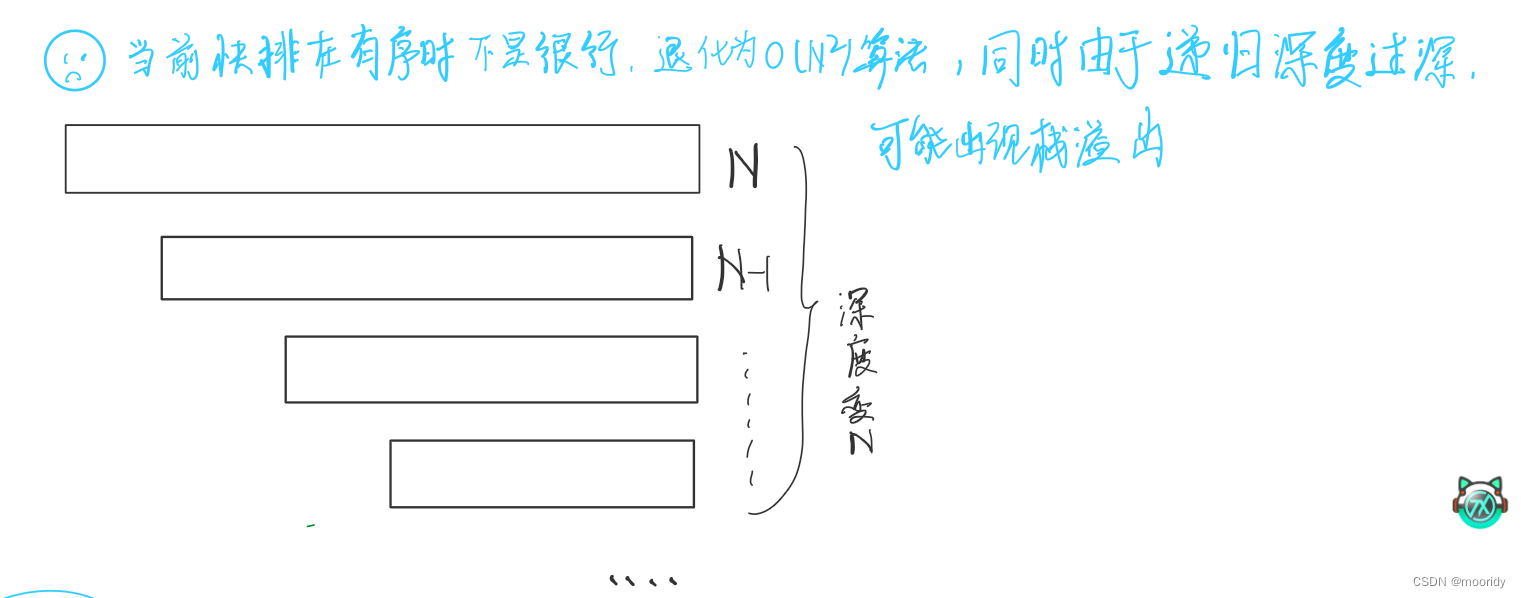
解决办法:改变选key的策略,采用三数选中的方法,使key不要老是为最小值,而尽量趋于中值。
即确定出三个索引,如left,right, (right-left)/2,选出三个索引对应的值为中值的索引。
//优化1:改变选key的策略,采用三数选中法
int FindMid(int* a, int left, int right) {int mid = (left + right) / 2;if (a[left] < a[right]) {if (a[left] < a[mid]) {if (a[mid] < a[right]) {//a[left]<a[mid]<a[right]return mid;}else {//a[left]<a[right]<a[mid]return right;}}else {//a[mid]<a[left]<a[right]return left;}}else {//a[left] > a[right]if (a[mid] > a[right]) {if (a[mid] > a[left]) {//a[mid] > a[left]> a[right]return left;}else {return mid;}}else {//a[left] > a[right]>a[mid]return right;}}
}
🍎优化2:小区间优化,采用其它排序方法,减少递归次数
冒泡排序、选择排序效率太一般,希尔排序更适合处理数据量更大的数据,此时的数据已经较为接近有序,此处采用插入排序。
//优化:小数区间,采取选择排序if (left + 5 >= right) {InsertSort(a+left, right - left + 1);return;}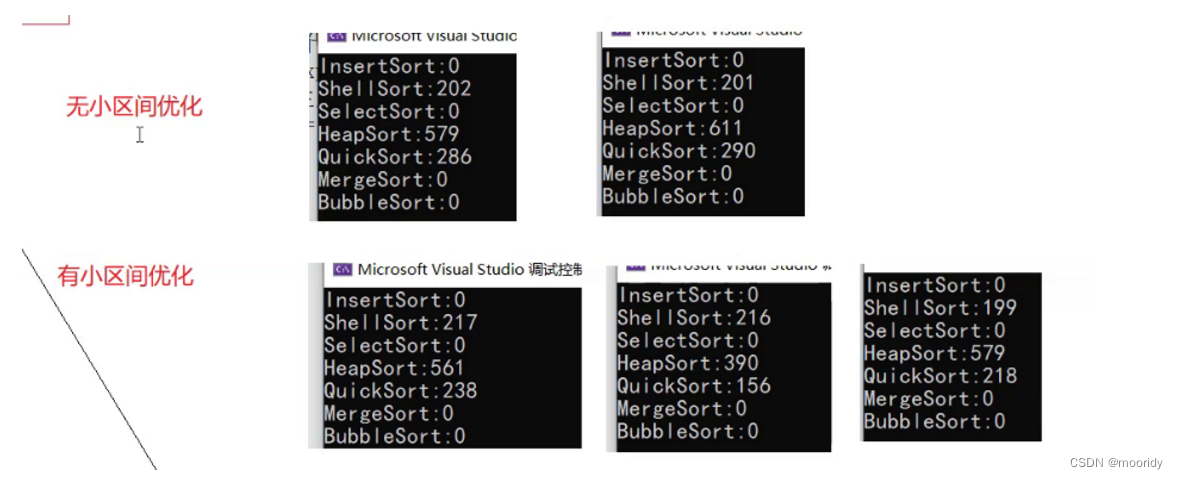
🍋思考:如何保证相遇位置比key小?
左边做key,右边先走,可以保证相遇位置比key小。
相遇场景分析:
begin遇end:end先走,停下来,一定是因为遇到了比key小的值。
begin再走,begin没有找到大的遇到end就停下了。
end遇begin:end走,end没有找到小的遇到begin就停下了。
而begin的位置此时还是上一轮交换的位置,而上一轮交换,把比key小的值换到了begin的位置。
🥳代码实现
1.基础版(递归)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
//递归版
void Swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}
void QuickSort(int* a, int left, int right) {//先考虑单趟//end找比key小,begin找比key大,都找到后交换//end,begin相遇时停止,交换begin和key//单趟过后的结果:key所在位置一定是正确的位置,a[left,key-1]一定小于key,a[key+1,right]一定大于key//接着就用递归思想处理:a[left,key-1],a[key+1,right]//递归结束条件:数组不存在或者只有1个元素if (left >= right) {return;}int begin = left;int end = right;int key = left;while (begin < end) {while (a[end] >= a[key] && begin < end) {end--;}while(a[begin] <= a[key]&&begin<end) {begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[key]);key = begin;//此时key需要改变QuickSort(a, left, key-1);QuickSort(a, key + 1, right);
}int main() {int a[10]={ 6, 1, 2, 7, 9, 3, 4, 5, 10,8 };QuickSort(a, 0, 9);for (int i = 0; i < 10; i++) {printf("%d ", a[i]);}return 0;
}2.优化版(递归)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
//递归版
void Swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}
//优化1:改变选key的策略,采用三数选中法
int FindMid(int* a, int left, int right) {int mid = (left + right) / 2;if (a[left] < a[right]) {if (a[left] < a[mid]) {if (a[mid] < a[right]) {//a[left]<a[mid]<a[right]return mid;}else {//a[left]<a[right]<a[mid]return right;}}else {//a[mid]<a[left]<a[right]return left;}}else {//a[left] > a[right]if (a[mid] > a[right]) {if (a[mid] > a[left]) {//a[mid] > a[left]> a[right]return left;}else {return mid;}}else {//a[left] > a[right]>a[mid]return right;}}
}void InsertSort(int* a, int n) {for (int i = 1; i < n ; i++) {int end = i;int tmp = a[end];while (end > 0) {if (tmp < a[end - 1]) {a[end] = a[end - 1];a[end - 1] = tmp;end--;}else {break;}}}
}void QuickSort(int* a, int left, int right){//先考虑单趟//end找比key小,begin找比key大,都找到后交换//end,begin相遇时停止,交换begin和key//单趟过后的结果:key所在位置一定是正确的位置,a[left,key-1]一定小于key,a[key+1,right]一定大于key//接着就用递归思想处理:a[left,key-1],a[key+1,right]//递归结束条件:数组不存在或者只有1个元素/*if (left >= right) {return;}*///优化:小数区间,采取选择排序if (left + 5 >= right) {InsertSort(a+left, right - left + 1);return;}int begin = left;int end = right;//优化:改变选key的策略,采用三数选中法int key = FindMid(a+left, left, right);Swap(&a[begin], &a[key]);key = begin;//int key = begin;while (begin < end) {while (a[end] >= a[key] && begin < end) {end--;}while(a[begin] <= a[key]&&begin<end) {begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[key]);key = begin;//此时key需要改变QuickSort(a, left, key-1);QuickSort(a, key + 1, right);
}int main(){int a[10]={ 6, 1, 2, 7, 9, 3, 4, 5, 10,8 };QuickSort(a, 0, 9);for (int i = 0; i < 10; i++) {printf("%d ", a[i]);}return 0;
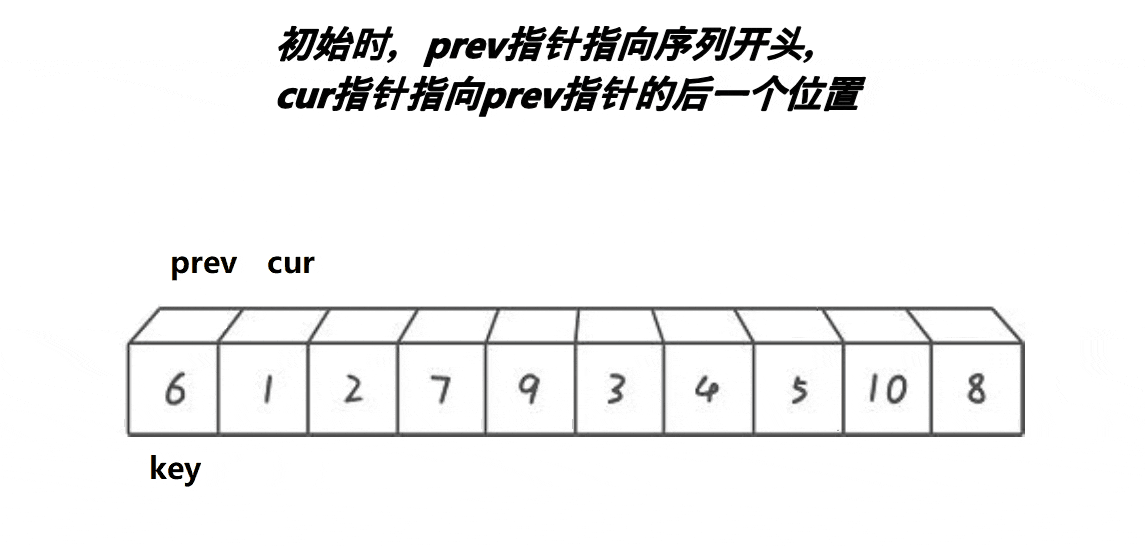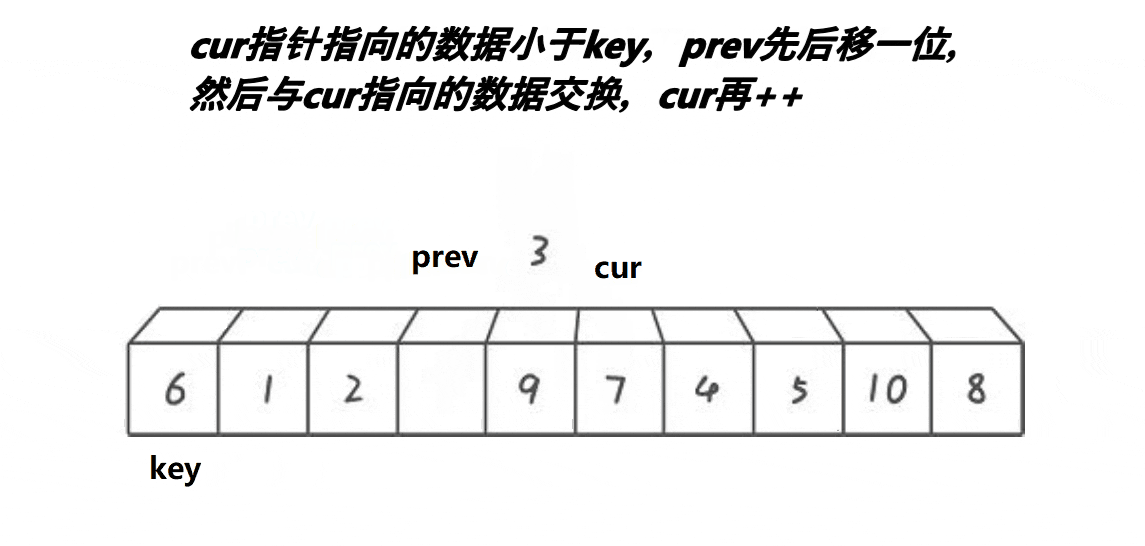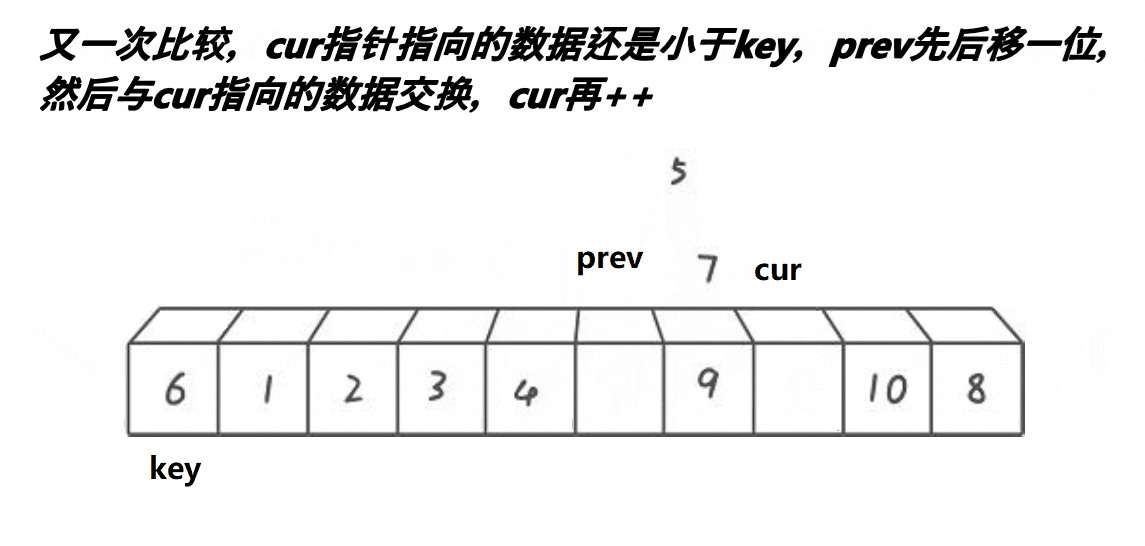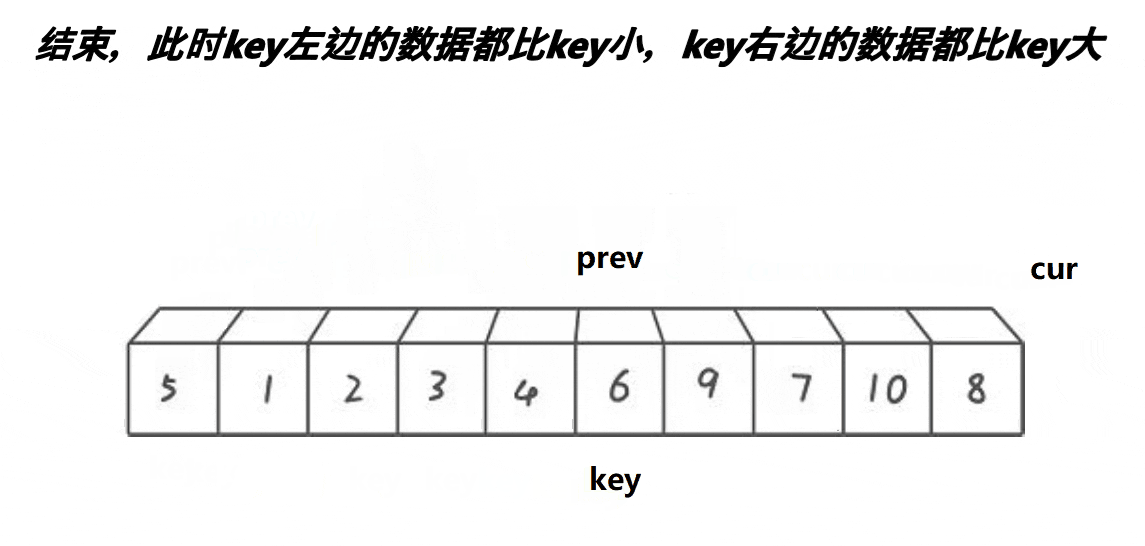
}🍹图解2:前后指针法
🌴深度剖析
🍎代码思路
仍然从单趟开始分析:
1.

2.判断cur指针指向的数据是否小于key:
小于——prev后移一位,交换cur和prev指向的内容,cur指针后移一位
大于——cur后移一位,效果:使得prev和cur之间的值全是大于key的值

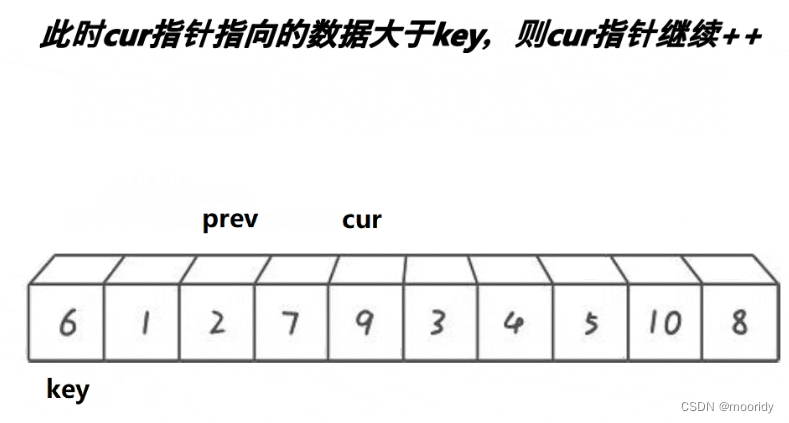
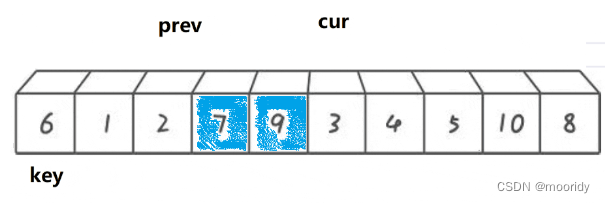
3.当cur越界,将prev指向的内容与key进行呼唤
效果:key左边的数据都比key小,key右边的数据都比key大
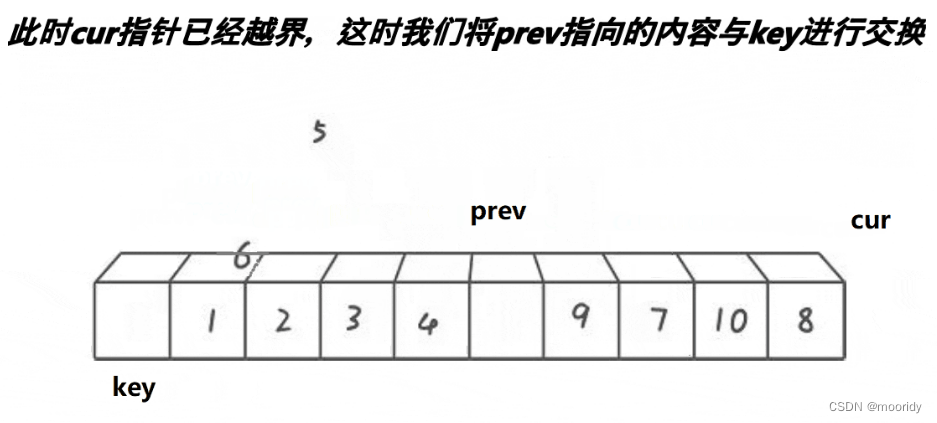
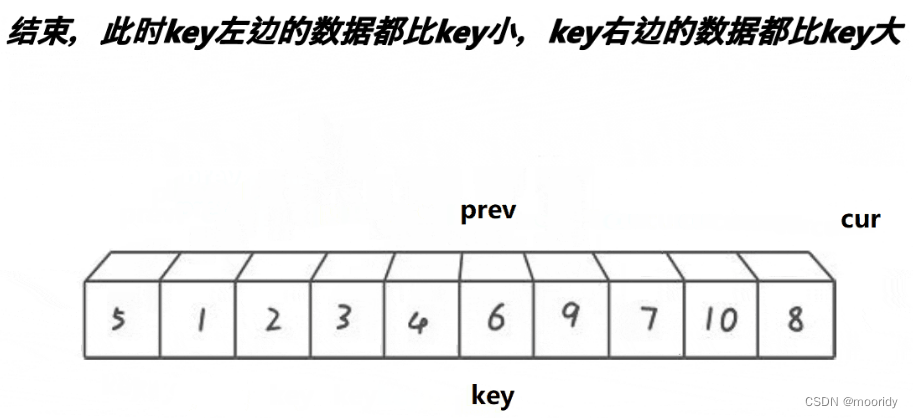
由于快慢指针法单趟后的效果和霍尔法其实是一致的,后续步骤就和霍尔法的步骤一模一样。
🍎优化:避免自己和自己交换
if (a[cur] < a[key] && ++prev != cur) {//优化:当++prev与cur重叠时,就不进行交换Swap(&a[cur], &a[prev]);}🥳代码实现
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void Swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}
//优化1:改变选key的策略,采用三数选中法
int FindMid(int* a, int left, int right) {int mid = (left + right) / 2;if (a[left] < a[right]) {if (a[left] < a[mid]) {if (a[mid] < a[right]) {//a[left]<a[mid]<a[right]return mid;}else {//a[left]<a[right]<a[mid]return right;}}else {//a[mid]<a[left]<a[right]return left;}}else {//a[left] > a[right]if (a[mid] > a[right]) {if (a[mid] > a[left]) {//a[mid] > a[left]> a[right]return left;}else {return mid;}}else {//a[left] > a[right]>a[mid]return right;}}
}void InsertSort(int* a, int n) {for (int i = 1; i < n; i++) {int end = i;int tmp = a[end];while (end > 0) {if (tmp < a[end - 1]) {a[end] = a[end - 1];a[end - 1] = tmp;end--;}else {break;}}}
}void QuickSort2(int* a, int left, int right) {if (left + 5 >= right) {InsertSort(a + left, right - left + 1);return;}//优化:改变选key的策略,采用三数选中法int key = FindMid(a + left, left, right);Swap(&a[left], &a[key]);key = left;int prev = left;int cur = left + 1;while (cur <= right) {if (a[cur] < a[key] && ++prev != cur) {//优化:当++prev与cur重叠时,就不进行交换Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[key], &a[prev]);key = prev;//此时key需要改变QuickSort2(a, left, key - 1);QuickSort2(a, key + 1, right);
}int main(){int a[10] = { 6, 1, 2, 7, 9, 3, 4, 5, 10,8 };QuickSort2(a, 0, 9);for (int i = 0; i < 10; i++) {printf("%d ", a[i]);}return 0;
}🍹非递归实现
🍎代码思路
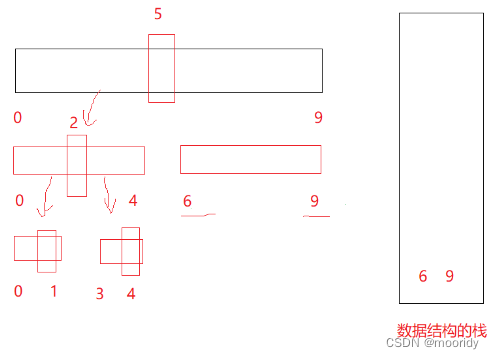
利用栈来模拟递归的过程,假设每次key值都刚好二分。
1.初始化一个栈,将right和left压入栈中
1.对数组进行单趟快速排序,得到[left,key-1],key,[key+1,right]
2.设begin1=left,end1=key-1
设begin2=key+1,end2=right
3.若begin2<end2,将end2,begin2压入栈中
若begin1<end1,将end1,begin1压入栈中
4.取并删除栈顶元素两次,得到begin1,end1,对[begin1,end1]数组进行单趟快速排序
5.重复步骤2,3,4,栈为空时循环结束
.
🥳代码实现
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include "stack.h"void Swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}void QuickSort(int* a, int left, int right) {Stack st;StackInit(&st);StackPush(&st, right);StackPush(&st, left);while (!StackEmpty(&st)) {left = StackTop(&st);StackPop(&st);right = StackTop(&st);StackPop(&st);int begin = left;int end = right;int key = begin;while (begin < end) {while (a[end] >= a[key] && begin < end) {end--;}while (a[begin] <= a[key] && begin < end) {begin++;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[key]);key = begin;//此时key需要改变int begin1 = left;int end1 = key - 1;int begin2 = key + 1;int end2 = right;if (begin2 < end2) {StackPush(&st, end2);StackPush(&st, begin2);}if (begin1 <end1) {StackPush(&st, end1);StackPush(&st, begin1);}}StackDestroy(&st);return;
}int main() {int a[10] = { 6, 1, 2, 7, 9, 3, 4, 5, 10,8 };QuickSort(a, 0, 9);for (int i = 0; i < 10; i++) {printf("%d ", a[i]);}return 0;
}7.归并排序
🍹图解
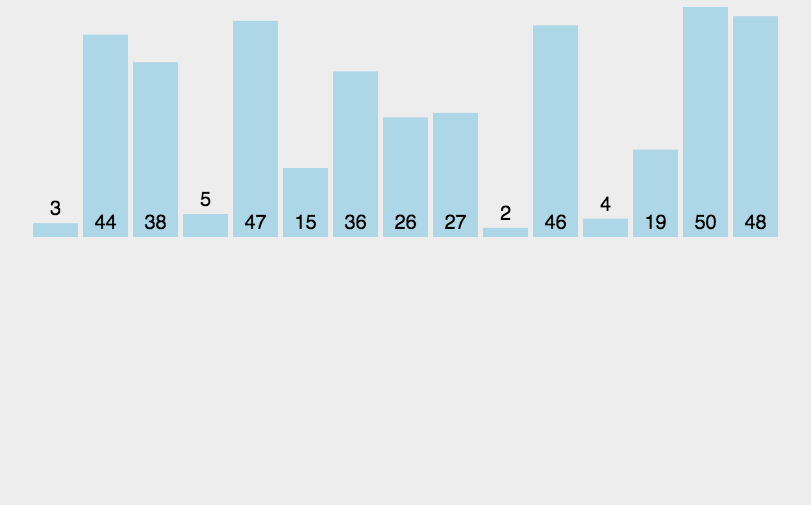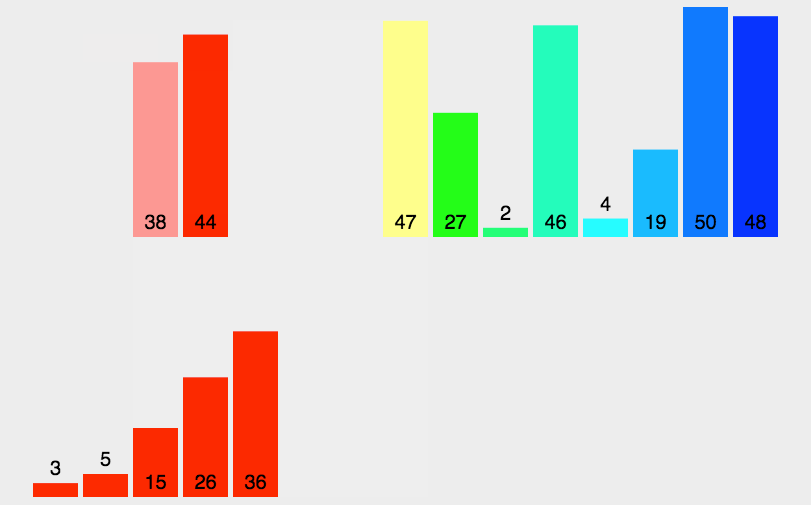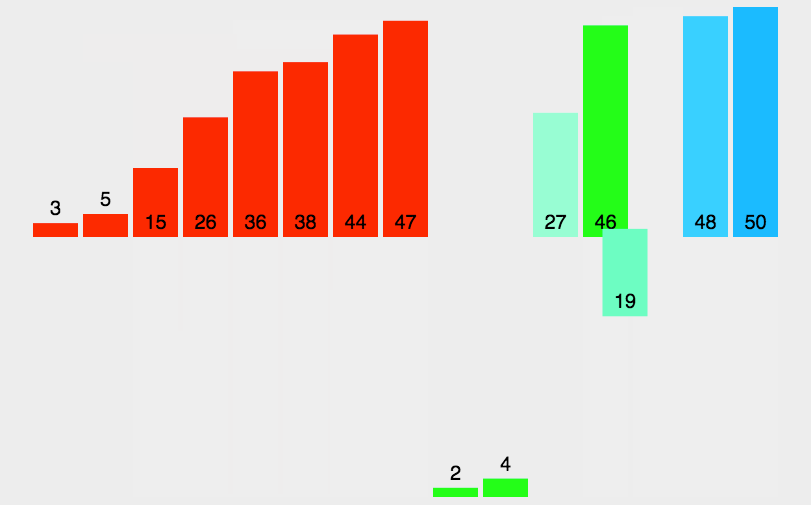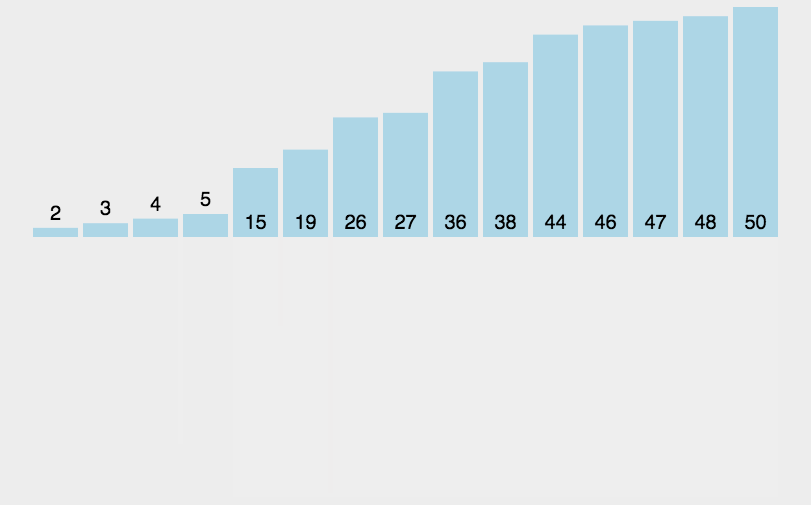
🌴深度剖析
基本思想:归并排序( MERGE-SORT )是建立在归并操作上的一种有效的排序算法 , 该算法是采用分治法 。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
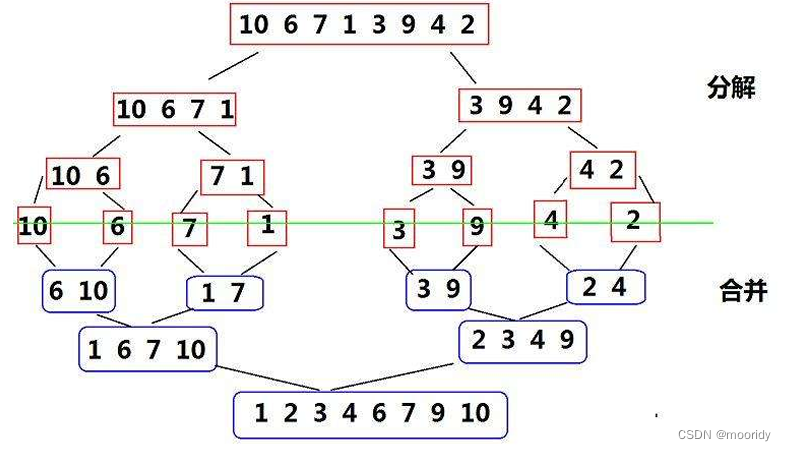
🍹递归版
🍎代码思路
假设数组可以被拆分成两个子数组:
比较begin1和begin2位置的值,
取小尾插到tmp,
被取指针向前移动
未被取指针,不动
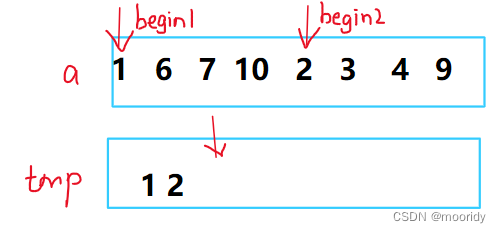
但问题是:数组往往不能直接被拆成两个有序数组
因此,考虑继续细分数组直到有序(比如只有1个数时必定有序)
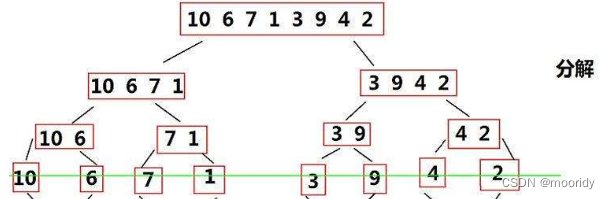
然后将有序子数组一层层的合并回去,每次合并完将结果拷贝回原数组。
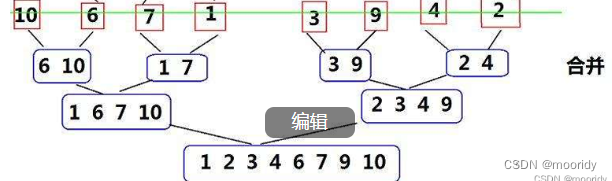
这个过程有点类似后序遍历。
🥳代码实现
void MergeSort1(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL) {perror("tmp malloc fail!");return;}if (n <= 1) {//当数组被拆分成单个数,或无法继续拆分,返回return;}int mid = (n+1)/ 2;//假设数组3个数,mid==2,MergeSort1(a, mid);//[0,mid-1]有序MergeSort1(a+mid, n-mid);//[mid,n-1]有序//合并两个有序数组int begin1 = 0;int end1 = mid - 1;int begin2 = mid;int end2 = n - 1;int tmp1 = 0;while (begin1 <=end1 && begin2 <= end2) {if (a[begin1] < a[begin2]) {//begin1的数比begin2小,尾插begin1tmp[tmp1] = a[begin1];begin1++;tmp1++;}else {tmp[tmp1] = a[begin2];begin2++;tmp1++;}}//循环结束,说明有一方指针已经走完//将另一方未走完指针走完while (begin1 <=end1) {tmp[tmp1] = a[begin1];begin1++;tmp1++;}while (begin2 <=end2) {tmp[tmp1] = a[begin2];begin2++;tmp1++;}//此时的tmp数组为有序数组//拷贝回原数组memcpy(a, tmp, sizeof(int) * n);
}🍹非递归版
🍎代码思路
1.首先设一个变量gap代表每组需要归并的个数。
2.划分两个大小为gap的子数组[begin1,end1],[begin2,end2],这两个数组应当是有序的,对其进行归并,归并完后,继续向后划分两个大小为gap的子数组,继续归并,直到整个数组被遍历完。
3.遍历完一次数组意味着以gap*2为大小的子数组已经有序,因此gap*=2,以新gap数,继续完成新一轮对数组的归并遍历。直到gap>=2,结束。
🍋思考:上面的思路只能解决数组大小为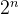 的数组,其余数组则会存在越界问题,如何解决?
的数组,其余数组则会存在越界问题,如何解决?
这是一个数据个数为10的数组:
![]()
打印每轮的合并情况,可发现,有些位置发生了越界:

将图示越界的位置抽象出来,即为:

解决方案:
判断begin2是否存在,若不存在,则结束归并,若存在则修正end2,使其不越界。
🥳代码实现
void MergeSort2(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL) {perror("tmp malloc fail!");return;}if (n <= 1) {//当数组被拆分成单个数,或无法继续拆分,返回return;}//后序遍历//合并两个有序数组int gap = 1;//每组需要归并的个数while(gap<n){//层序遍历for(int i=0;i<n;i+=2*gap){int begin1 = i;int end1 = i+gap-1;int begin2 = i+gap;int end2 = i+2*gap-1;int j = i;if (begin2 >= n) {break;}if (end2 >= n) {end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2) {if (a[begin1] < a[begin2]) {//begin1的数比begin2小,尾插begin1tmp[j++] = a[begin1];begin1++;}else {tmp[j++] = a[begin2];begin2++;}}//循环结束,说明有一方指针已经走完//将另一方未走完指针走完while (begin1 <= end1) {tmp[j++] = a[begin1];begin1++;}while (begin2 <= end2) {tmp[j++] = a[begin2];begin2++;}//此时的tmp数组为有序数组//拷贝回原数组memcpy(a+i, tmp+i, sizeof(int) * (end2-i+1));//易错点:(end2-begin1+1)是错的,因为begin1这个时候已经不再是子数组起点位置}gap *= 2;}}int main() {int a1[8] = { 10,6,7,1,3,9,4,2 };int a2[16] = { 16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1 };int a3[12] = { 12,11,10,9,8,7,6,5,4,3,2,1 };MergeSort2(a1, 8);for (int i = 0; i < 8; i++) {printf("%d ", a1[i]);}printf("\n");MergeSort2(a2, 16);for (int i = 0; i < 16; i++) {printf("%d ", a2[i]);}MergeSort2(a3, 12);printf("\n");for (int i = 0; i < 12; i++) {printf("%d ", a3[i]);}}🤔时间复杂度
O(N*logN)
相关文章:

数据结构 | 超详细讲解七大排序(C语言实现,含动图,多方法!)
目录 编辑 排序的概念 常见排序算法 编辑 1.冒泡排序 🍹图解 🥳代码实现 🤔时间复杂度 2.插入排序 🍹图解 🌴深度剖析 🍎代码思路 🥳代码实现 🤔时间复杂度 3.希尔…...

企业自建邮件系统的优势,安全性更高,功能更灵活,维护更便捷
在当今企业信息管理的浪潮中,企业邮件系统显得尤为关键,它不仅加强了内部的沟通效率,还对外展示了企业的专业形象。然而,传统租用企业邮箱服务存在一些不足,如缺乏灵活性、数据管理混乱和难以实现个性化需求࿰…...

Softing工业助力微软解锁工业数据,推动AI技术在工业领域的发展
一 概览 Softing作为全球先进工业通信解决方案供应商之一,与微软合作共同推出了众多工业边缘产品,以实现工业应用中OT和IT的连接。这些产品可在基于微软Azure云平台的IIoT解决方案中轻松集成和运行,并为AI解锁工业数据,还可通过A…...

企微自动化机器人的应用与前景
一、引言 随着信息技术的飞速发展,企业对于提高内部运营效率、降低人力成本的需求日益迫切。在这样的背景下,企微自动化机器人应运而生,以其高效、便捷的特点,迅速成为企业内部的得力助手。本文将深入探讨企微自动化机器人的应用现…...

从零开始:如何用Electron将chatgpt-plus.top 打包成EXE文件
文章目录 从零开始:如何用Electron将chatgpt-plus.top 打包成EXE文件准备工作:Node.js和npm国内镜像加速下载初始化你的Electron项目创建你的Electron应用运行你的Electron应用为你的应用设置图标打包成EXE文件结语 从零开始:如何用Electron将…...

基于RNN和Transformer的词级语言建模 代码分析 log_softmax
基于RNN和Transformer的词级语言建模 代码分析 log_softmax flyfish Word-level Language Modeling using RNN and Transformer word_language_model PyTorch 提供的 word_language_model 示例展示了如何使用循环神经网络RNN(GRU或LSTM)和 Transformer 模型进行词级语言建模…...

Python爬虫要掌握哪些东西
学习Python爬虫,你需要掌握以下几个关键方面的知识: 文章目录 Python基础:首先,确保你对Python语言有良好的理解,包括基本语法、数据结构(如列表、字典、集合等)、函数、类和对象、模块和包的使用等。# 有一个数字列表,要创建新的列表,元素是原列表中每个元素的平方 …...
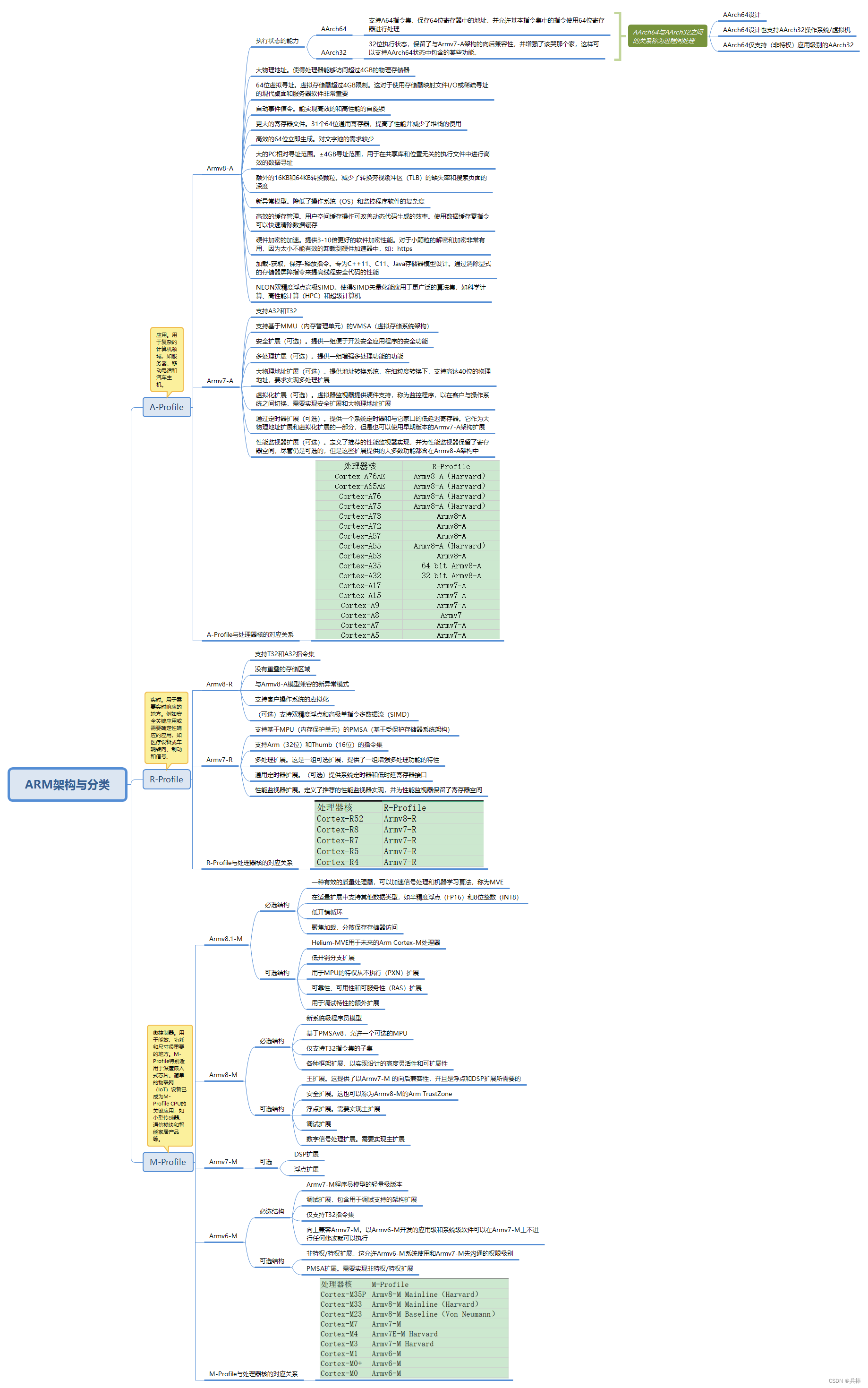
FPGA-ARM架构与分类
ARM架构,曾称进阶精简指令集机器(Advanced RISC Machine)更早称作Acorn RISC Machine,是一个32位精简指令集(RISC)处理器架构。 主要是根据FPGA zynq-7000的芯片编写的知识思维导图总结,废话不多说自取吧 …...
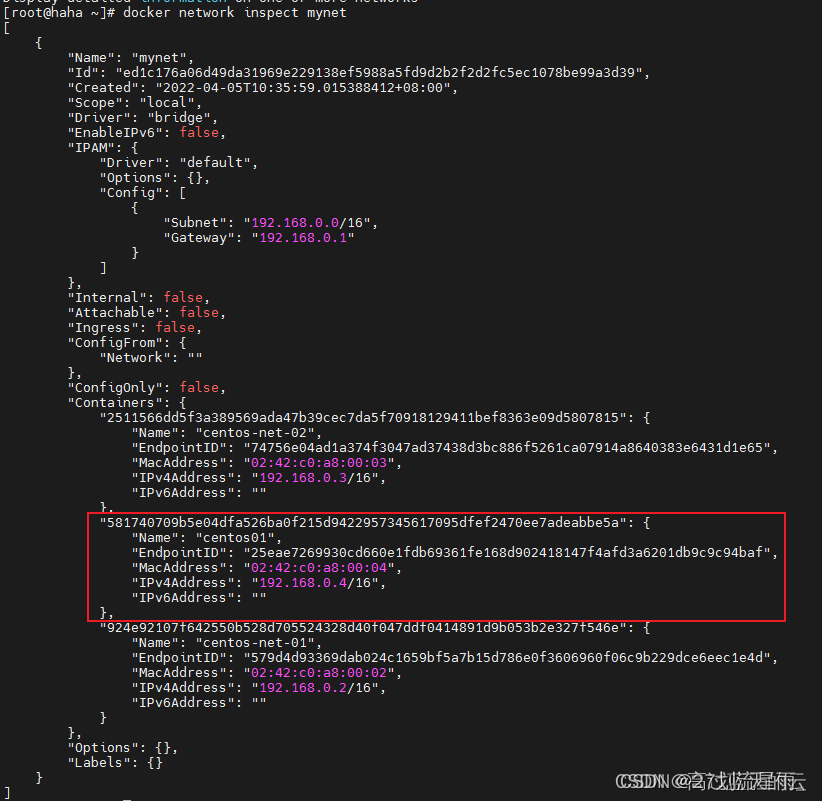
docker网络详解
1. 网络模式 1.1 网络结构 当安装Docker以后,会自动创建三个网络。可以使用docker network ls命令列出这些网络。 $ docker network ls NETWORK ID NAME DRIVER SCOPE 440aefe8afa3 bridge bridge local aa8d6325580f host host …...
设计软件有哪些?效果工具篇(1),渲染100邀请码1a12
设计师会用到很多渲染效果和后期处理的工具,这里我们介绍一些。 1、AfterBurn AfterBurn是为Autodesk 3ds Max开发的专业级别的体积照明和效果插件。它提供了一系列强大的特效功能,包括烟雾、火焰、云彩等。用户可以利用AfterBurn创建逼真的环境效果&a…...

Iphone自动化指令每隔固定天数打开闹钟关闭闹钟(二)
1.首先在搜索和操作里搜索“查找日期日程" 1.1.然后过滤条件开始日期选择”是今天“ 1.2.增加过滤条件,日历是这里选择”工作“ 1.3.增加过滤条件,选择标题,是这里选择”workDay“ 1.4选中限制,日历日程只要一个,…...

计算机网络错题答案汇总
王道学习 第1章 计算机网络体系结构 1.1 1.2...

Fortigate防火墙二层接口的几种实现方式
初始配置 FortiGate出厂配置默认地址为192.168.1.99(MGMT接口),可以通过https的方式进行web管理(默认用户名admin,密码为空),不同型号设备用于管理的接口略有不同。 console接口的配置 防火墙…...
如何永久擦除Android手机中的所有个人数据?
在这个数字化的时代,确保您的个人数据的安全和隐私至关重要。如果您计划出售或回收您的Android手机,了解如何正确擦除Android手机是至关重要的。本综合指南将引导您通过安全擦除Android手机的分步过程,以保护您的敏感信息。 手机是极其敏感的…...

使用手机小程序给证件照换底色
临时遇到一个需求,需要给证件照换底色。原始图像如下 最终需要换成红底的。 本次使用一款小程序"泰世茂证件照",打开该小程序,如下图所示 单击开始制作,然后选择二寸红底,如下图所示 然后单击相…...
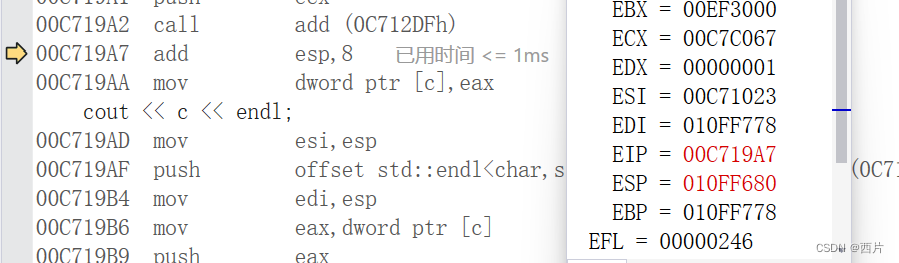
C语言杂谈:函数栈帧,函数调用时到底发生了什么
我们都知道在调用函数时,要为函数在栈上开辟空间,函数后续内容都会在栈帧空间中保存,如非静态局部变量,返回值等。这段空间就叫栈帧。 当函数调用,就会开辟栈帧空间,函数返回时,栈帧空间就会被释…...
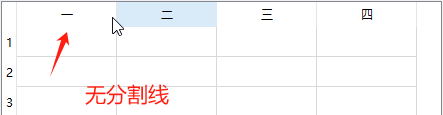
【Qt】win10,QTableWidget表头下无分隔线的问题
1. 现象 2. 原因 win10系统的UI样式默认是这样的。 3. 解决 - 方法1 //横向表头ui->table->horizontalHeader()->setStyleSheet("QHeaderView::section{""border-top:0px solid #E5E5E5;""border-left:0px solid #E5E5E5;""bord…...

前端 实现有时间限制的缓存
首先我们需要创建一个名为TimeLimitedCache的构造函数,然后定义一些方法,如set, get,和count。以下是具体的示例代码: // 定义 TimeLimitedCache 构造函数 var TimeLimitedCache function( ) {// 初始化一个空的 cache 对象,用于…...
前端将xlsx转成json
第一种方式,用js方式 1.1先安装插件 万事都离不开插件的支持首先要安装两个插件 1.2. 安装xlsx cnpm install xlsx --save注:这块我用的cnpm,原生的是npm,因为镜像的问题安装了cnpm,至于怎么装网上一搜一大堆 1.3安…...
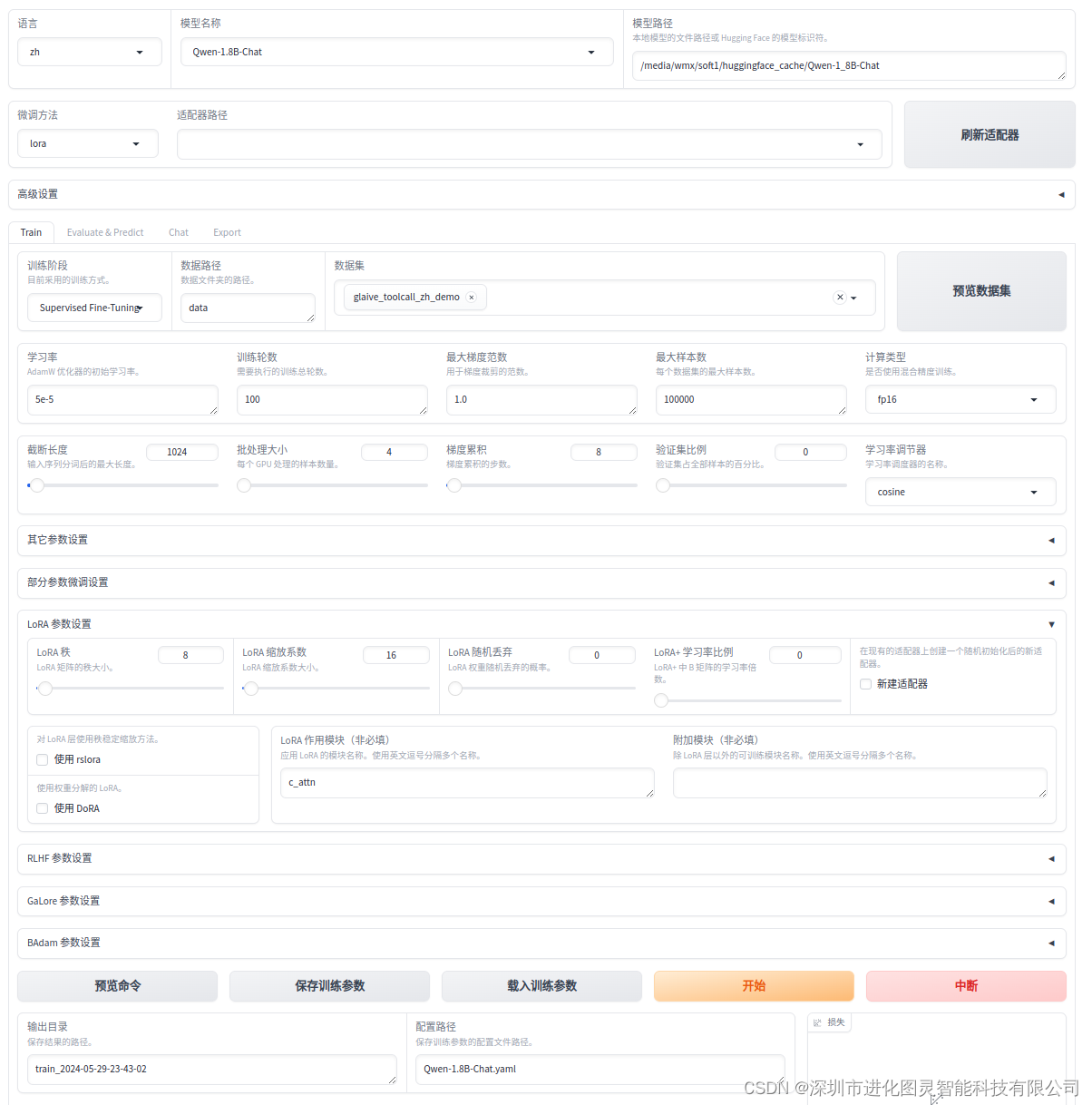
使用LLaMA-Factory微调大模型
使用LLaMA-Factory微调大模型 github 地址 https://github.com/hiyouga/LLaMA-Factory 搭建环境 git clone --depth 1 https://github.com/hiyouga/LLaMA-Factory.git cd LLaMA-Factory在 LLaMA-Factory 路径下 创建虚拟环境 conda create -p ./venv python3.10激活环境 c…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...