【力扣】矩阵中的最长递增路径
一、题目描述
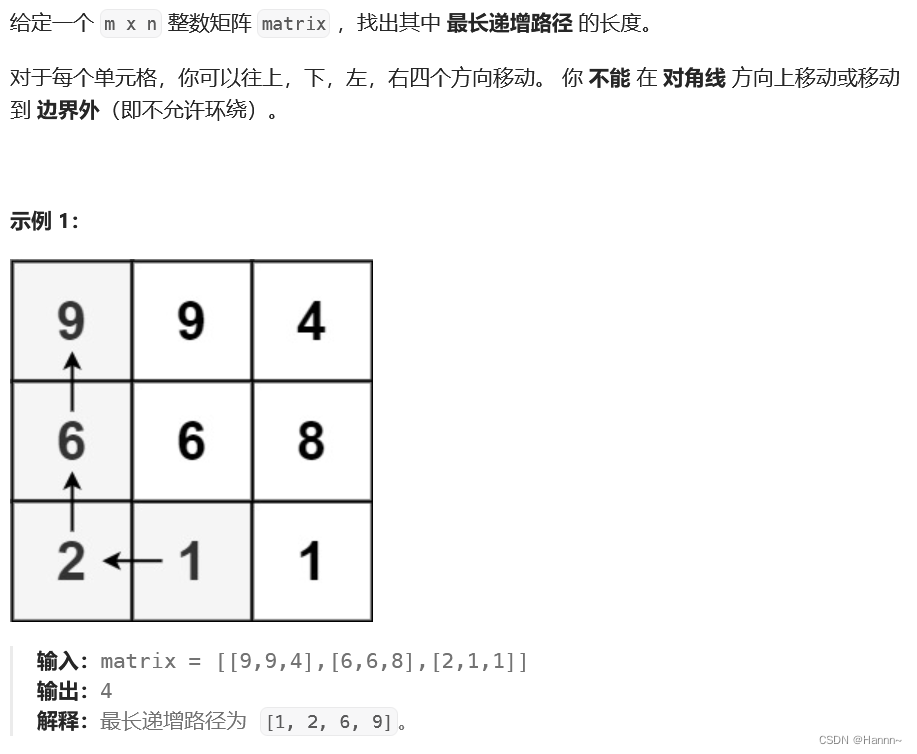
二、解题思路
1、先求出以矩阵中的每个单元格为起点的最长递增路径
题目中说,对于每个单元格,你可以往上,下,左,右四个方向移动。那么以一个单元格为起点的最长递增路径就是:从该单元格往上,下,左,右四个方向走的四条递增路径中的最大值(即最长的一条递增路径)。
2、在求出的所有最长递增路径中找最大值
因为题目是求矩阵中的最长递增路径,所以要在求出的所有最长递增路径中找最大值。
3、使用“记忆化搜索”(递归+“备忘录” )来解决该题。
三、 代码
class Solution {int m, n;//遍历上、下、左、右四个方向所需的数组int[] dx = {0,0,1,-1};int[] dy = {1,-1,0,0};int[][] memo; //备忘录public int longestIncreasingPath(int[][] matrix) {m = matrix.length;n = matrix[0].length;memo = new int[m][n];//求所有的最长递增路径中的最大值int ret = 0;for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {ret = Math.max(ret,dfs(i, j, matrix));}}return ret;}//递归函数//求出以矩阵中的每个单元格为起点的最长递增路径(上下左右四个方向中的最大值)public int dfs(int i, int j, int[][] matrix) {if(memo[i][j] != 0) {return memo[i][j];}int ret = 1;for(int k = 0; k < 4; k++) {int x = i + dx[k];int y = j + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) {ret = Math.max(ret, dfs(x,y,matrix)+1);}}memo[i][j] = ret;return ret;}
}
相关文章:

【力扣】矩阵中的最长递增路径
一、题目描述 二、解题思路 1、先求出以矩阵中的每个单元格为起点的最长递增路径 题目中说,对于每个单元格,你可以往上,下,左,右四个方向移动。那么以一个单元格为起点的最长递增路径就是:从该单元格往上…...
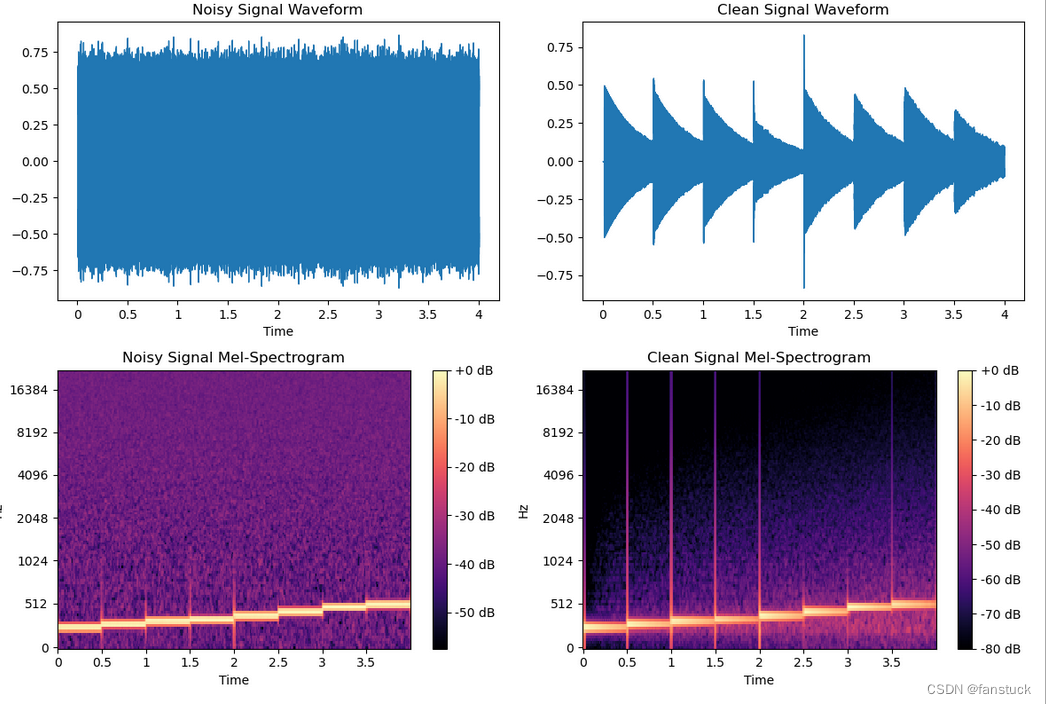
语音深度鉴伪识别项目实战:基于深度学习的语音深度鉴伪识别算法模型(二)音频数据预处理及去噪算法+Python源码应用
前言 深度学习技术在当今技术市场上面尚有余力和开发空间的,主流落地领域主要有:视觉,听觉,AIGC这三大板块。 目前视觉板块的框架和主流技术在我上一篇基于Yolov7-LPRNet的动态车牌目标识别算法模型已有较为详细的解说。与AIGC相…...

网络原理——http/https ---http(1)
T04BF 👋专栏: 算法|JAVA|MySQL|C语言 🫵 今天你敲代码了吗 网络原理 HTTP/HTTPS HTTP,全称为"超文本传输协议" HTTP 诞⽣与1991年. ⽬前已经发展为最主流使⽤的⼀种应⽤层协议. 实际上,HTTP最新已经发展到 3.0 但是当前行业中主要使用的HT…...
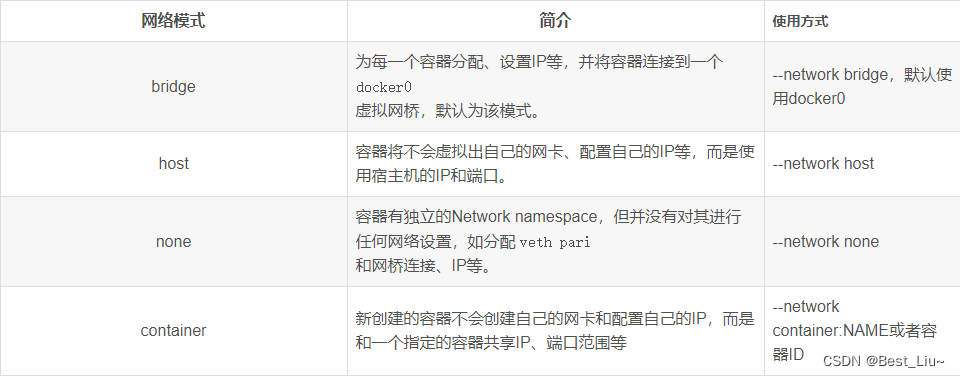
Docker安装、使用,容器化部署springboot项目
目录 一、使用官方安装脚本自动安装 二、Docker离线安装 1. 下载安装包 2. 解压 3.创建docker.service文件 4. 启动docker 三、docker常用命令 1. docker常用命令 2. docker镜像命令 3. docker镜像下载 4.docker镜像push到仓库 5. docker操作容器 6.docker …...
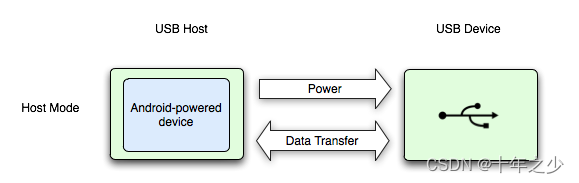
USB主机模式——Android
理论 摘自:USB 主机和配件概览 | Connectivity | Android Developers (google.cn) Android 通过 USB 配件和 USB 主机两种模式支持各种 USB 外围设备和 Android USB 配件(实现 Android 配件协议的硬件)。 在 USB 主机模式下࿰…...

240520Scala笔记
240520Scala笔记 第 7 章 集合 7.1 集合1 数组Array 集合(Test01_ImmutableArray): package chapter07 object Test01_ImmutableArray {def main(args: Array[String]): Unit {// 1. 创建数组val arr: Array[Int] new Array[Int](5)// 另一种创建方式val arr2 Array(…...
【React】封装一个好用方便的消息框(Hooks Bootstrap 实践)
引言 以 Bootstrap 为例,使用模态框编写一个简单的消息框: import { useState } from "react"; import { Modal } from "react-bootstrap"; import Button from "react-bootstrap/Button"; import bootstrap/dist/css/b…...
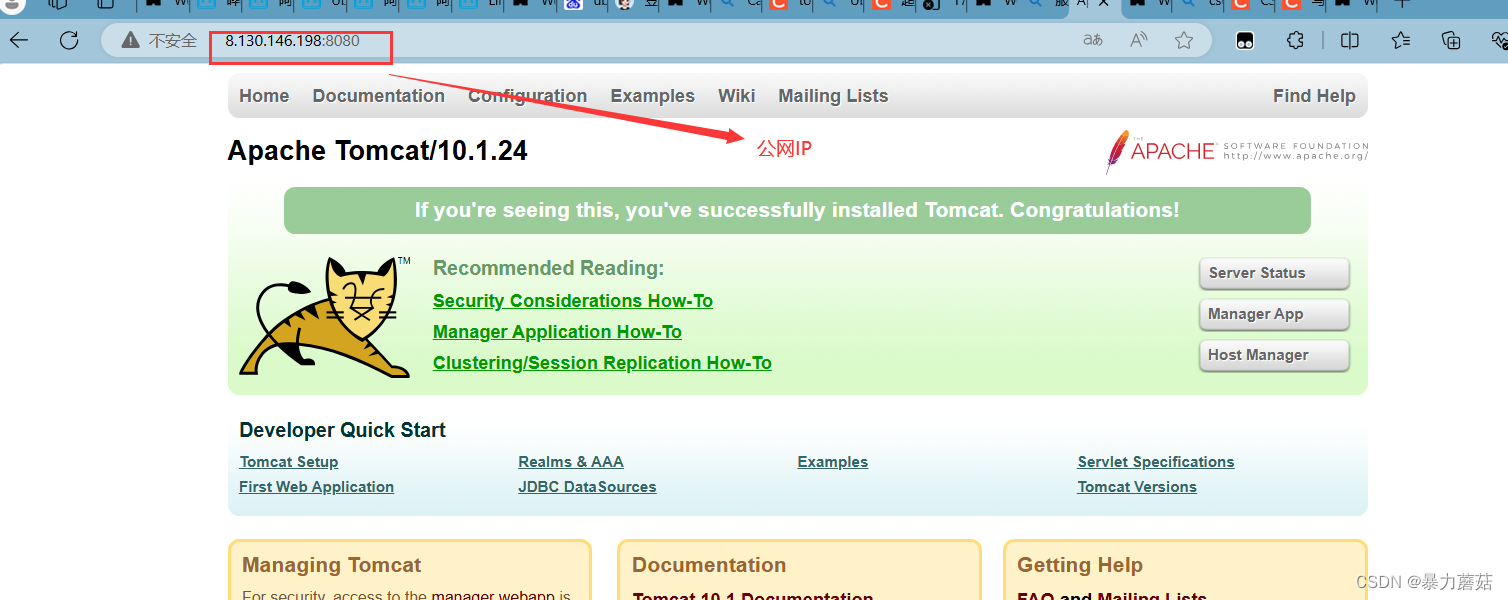
tomcat10部署踩坑记录-公网IP和服务器系统IP搞混
1. 服务器基本条件 使用的阿里云服务器,镜像系统是Ubuntu16.04java version “17.0.11” 2024-04-16 LTS装的是tomcat10.1.24阿里云服务器安全组放行了:8080端口 服务器防火墙关闭: 监听情况和下图一样: tomcat正常启动ÿ…...

探索Sass:Web开发的强大工具
在现代Web开发中,CSS(层叠样式表)作为前端样式设计的核心技术,已经发展得非常成熟。然而,随着Web应用的复杂性不断增加,传统的CSS书写方式逐渐暴露出一些不足之处,如代码冗长、难以维护、缺乏编程功能等。为了解决这些问题,Sass(Syntactically Awesome Stylesheets)应…...

vue组件之间的通信方式有哪些
在开发过程中,数据传输是一个核心的知识点,掌握了数据传输,相当于掌握了80%的内容。 Vue.js 提供了多种组件间的通信方式,这些方式适应不同的场景和需求。下面是4种常见的通信方式: 1. Props & Events (父子组件通…...
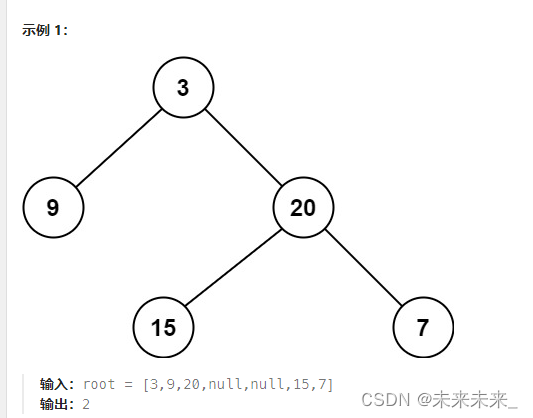
111、二叉树的最小深度
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 题解:找出最小深度也就是找出根节点相对所有叶子结点的最小高度,在这也表明了根节点的高度是变化的,相对不同的叶子结点有不同的高度。…...
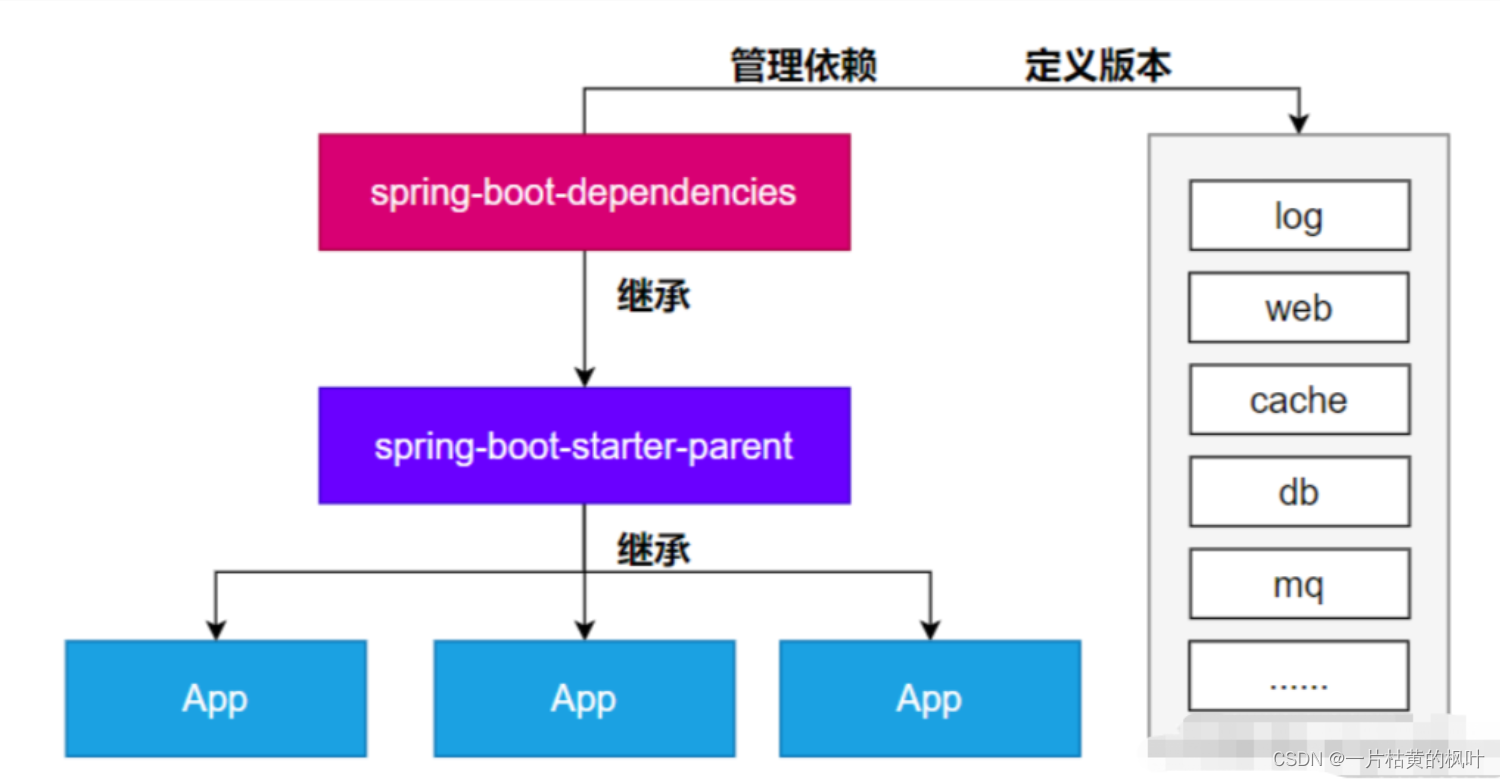
SpringBoot3依赖管理,自动配置
文章目录 1. 项目新建2. 相关pom依赖3. 依赖管理机制导入 starter 所有相关依赖都会导入进来为什么版本号都不用写?如何自定义版本号第三方的jar包 4. 自动配置机制5. 核心注解 1. 项目新建 直接建Maven项目通过官方提供的Spring Initializr项目创建 2. 相关pom依…...

音视频开发17 FFmpeg 音频解码- 将 aac 解码成 pcm
这一节,接 音视频开发12 FFmpeg 解复用详情分析,前面我们已经对一个 MP4文件,或者 FLV文件,或者TS文件进行了 解复用,解出来的 视频是H264,音频是AAC,那么接下来就要对H264和AAC进行处理,这一节…...
)
vue2中封装图片上传获取方法类(针对后端返回的数据不是图片链接,只是图片编号)
在Vue 2中实现商品列表中带有图片编号,并将返回的图片插入到商品列表中,可以通过以下步骤完成: 在Vue组件的data函数中定义商品列表和图片URL数组。 创建一个方法来获取每个商品的图片URL。 使用v-for指令在模板中遍历商品列表,并…...
this指针和静态成员)
【C++面向对象编程】(二)this指针和静态成员
文章目录 this指针和静态成员this指针静态成员 this指针和静态成员 this指针 C中类的成员变量和成员函数的存储方式有所不同: 成员变量:对象的成员变量直接作为对象的一部分存储在内存中。成员函数:成员函数(非静态成员函数&am…...
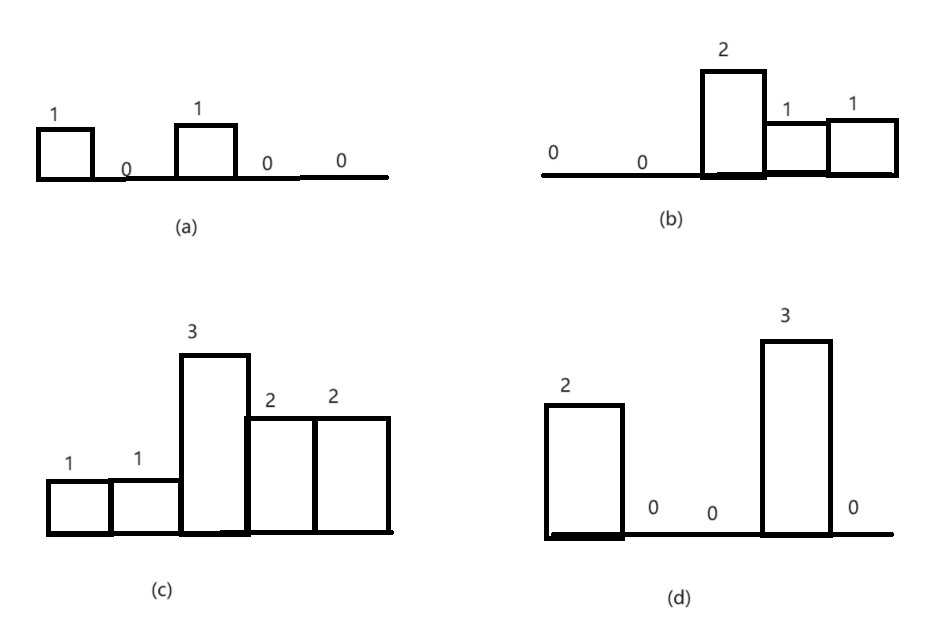
最大矩形问题
柱状图中最大的矩形 题目 分析 矩形的面积等于宽乘以高,因此只要能确定每个矩形的宽和高,就能计算它的面积。如果直方图中一个矩形从下标为 i 的柱子开始,到下标为 j 的柱子结束,那么这两根柱子之间的矩形(含两端的柱…...

LeetCode62不同路径
题目描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径? …...
GNU Radio实现OFDM Radar
文章目录 前言一、GNU Radio Radar Toolbox编译及安装二、ofdm radar 原理讲解三、GNU Radio 实现 OFDM Radar1、官方提供的 grc①、grc 图②、运行结果 2、修改后的便于后续可实现探测和通信的 grc①、grc 图②、运行结果 四、资源自取 前言 本文使用 GNU Radio 搭建 OFDM Ra…...

东方博宜1760 - 整理抽屉
题目描述 期末考试即将来临,小T由于同时肩负了学习、竞赛、班团活动等多方面的任务,一直没有时间好好整理他的课桌抽屉,为了更好地复习,小T首先要把课桌抽屉里的书分类整理好。 小T的抽屉里堆着 N 本书,每本书的封面上…...
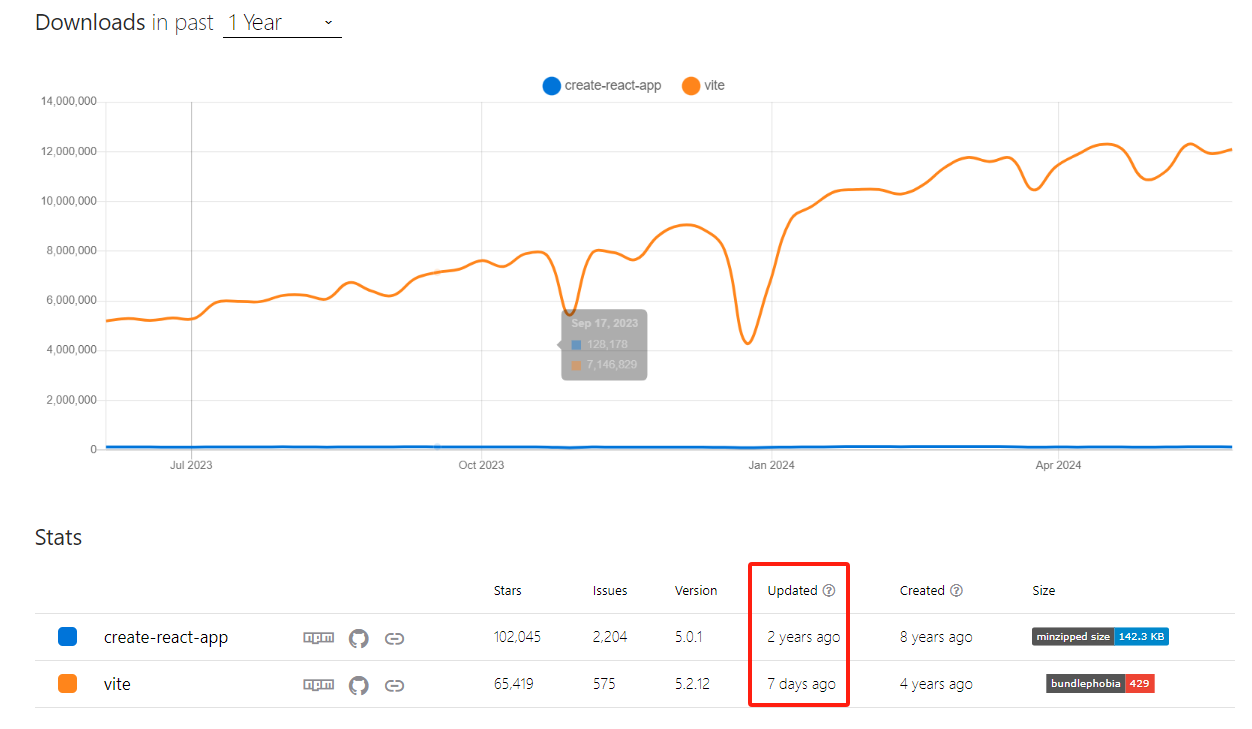
react快速开始(四)-之Vite 还是 (Create React App) CRA? 用Vite创建项目
文章目录 react快速开始(四)-之Vite 还是 (Create React App) CRA? 用Vite创建项目背景Vite 和 (Create React App) CRAVite?Vite 是否支持 TypeScript? 用Vite创建react项目参考 react快速开始(四)-之Vite 还是 (Create React App) CRA? 用Vite创建项…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
