矩阵1-范数与二重求和的求和可交换
矩阵1-范数与二重求和的求和可交换
1、矩阵1-范数
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] A = \begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots &\ddots &\vdots \\ a_{n1} &a_{n2} &\cdots &a_{nn} \\ \end{bmatrix} A= a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann
∣ ∣ A ∣ ∣ m 1 = ∑ i = 1 n ( ∑ j = 1 n ∣ a i j ∣ ) = ∑ j = 1 n ( ∑ i = 1 n ∣ a i j ∣ ) ||A||_{m1} = \sum_{i=1}^{n} (\sum_{j=1}^{n}|a_{ij}|) = \sum_{j=1}^{n} (\sum_{i=1}^{n}|a_{ij}|) ∣∣A∣∣m1=i=1∑n(j=1∑n∣aij∣)=j=1∑n(i=1∑n∣aij∣)
2、二重求和的求和符号可交换
对于矩阵1-范数而言,求和符号交换前后是按行求和与按列求和的区别。本质上都是把每个元素取模并相加。
再讨论一个例子,自相关函数 r ( m ) r(m) r(m)。
对于一个广义平稳离散时间随机过程 u ( n ) u(n) u(n)而言,其自相关函数定义为:
r ( m ) = E { u ( n ) u ∗ ( n − m ) } = ∫ ∫ u ( n ) u ∗ ( n − m ) p ( u n , u n − m ; n , n − m ) d u n d u n − m r(m) = E\{u(n)u^*(n-m)\} = \int\int u(n)u^*(n-m)p(u_n,u_{n-m};n,n-m)\mathrm{d}u_n \mathrm{d}u_{n-m} r(m)=E{u(n)u∗(n−m)}=∫∫u(n)u∗(n−m)p(un,un−m;n,n−m)dundun−m
其中 E E E是求期望, p ( ) p() p()表示联合概率密度函数。积分范围是 u ( n ) u(n) u(n)的值域,作为离散时间信号,值域不一定是离散的,值域经过量化后称为“数字信号”。
假设观测了N个采样点,那么可以得到 u ( n ) u(n) u(n)的离散傅立叶变换DFT:
U ( k ) = ∑ n = 0 N − 1 u ( n ) e − j 2 π N k n U(k) = \sum_{n=0}^{N-1} u(n) e^{-j\frac{2\pi}{N}kn} U(k)=n=0∑N−1u(n)e−jN2πkn
在信号处理领域,通常会从0开始编号,也比较符合实际,电路采样一般从一个时钟上升边沿开始算起。
当我们考虑 U ( k ) U(k) U(k)的自相关函数的时候:
r U ( m ) = E { U ( k ) U ∗ ( k − m ) } = E { ∑ n = 0 N − 1 u ( n ) e − j 2 π N k n ∑ l = 0 N − 1 u ( l ) e j 2 π N ( k − m ) l } r_U(m) = E\{U(k)U^*(k-m)\} = E\{\sum_{n=0}^{N-1} u(n) e^{-j\frac{2\pi}{N}kn}\sum_{l=0}^{N-1} u(l) e^{j\frac{2\pi}{N}(k-m)l}\} rU(m)=E{U(k)U∗(k−m)}=E{n=0∑N−1u(n)e−jN2πknl=0∑N−1u(l)ejN2π(k−m)l}
注意到这里出现了两个和相乘的形式,那么根据多项式乘法规则,应该得到 N 2 N^2 N2项之和。
这个时候就可以写成:
r U ( m ) = E { ∑ n = 0 N − 1 ∑ l = 0 N − 1 u ( n ) u ( l ) e − j 2 π N k n e j 2 π N ( k − m ) l } r_U(m) =E\{\sum_{n=0}^{N-1} \sum_{l=0}^{N-1} u(n)u(l) e^{-j\frac{2\pi}{N}kn} e^{j\frac{2\pi}{N}(k-m)l}\} rU(m)=E{n=0∑N−1l=0∑N−1u(n)u(l)e−jN2πknejN2π(k−m)l}
抽象一下:
考虑两个序列 a = ( a 1 , a 2 , ⋯ , a n ) T a = (a_1,a_2,\cdots,a_n)^T a=(a1,a2,⋯,an)T和 b = ( b 1 , b 2 , ⋯ , b n ) T b=(b_1,b_2,\cdots,b_n)^T b=(b1,b2,⋯,bn)T的1-范数相乘,
∣ ∣ a ∣ ∣ 1 ⋅ ∣ ∣ b ∣ ∣ 1 = ∑ i = 1 n ∣ a i ∣ ∑ j = 1 n ∣ b j ∣ = ∑ i = 1 n ∑ j = 1 n ∣ a i ∣ ∣ b j ∣ = ∑ i = 1 n ∑ j = 1 n ∣ a i b j ∣ ||a||_1\cdot ||b||_1 = \sum_{i=1}^n|a_i| \sum_{j=1}^n |b_j| = \sum_{i=1}^n \sum_{j=1}^n |a_i||b_j| = \sum_{i=1}^n \sum_{j=1}^n |a_ib_j| ∣∣a∣∣1⋅∣∣b∣∣1=i=1∑n∣ai∣j=1∑n∣bj∣=i=1∑nj=1∑n∣ai∣∣bj∣=i=1∑nj=1∑n∣aibj∣
实际上可以表示成一个矩阵:
[ a 1 b 1 a 1 b 2 ⋯ a 1 b n a 2 b 1 a 2 b 2 ⋯ a 2 b 2 ⋮ ⋮ ⋱ ⋮ a n b 1 a n b 2 ⋯ a n b n ] \begin{bmatrix} a_1 b_1 &a_1 b_2 &\cdots &a_1 b_n \\ a_2 b_1 &a_2 b_2 &\cdots &a_2 b_2 \\ \vdots &\vdots &\ddots &\vdots \\ a_n b_1 &a_n b_2 &\cdots &a_n b_n \\ \end{bmatrix} a1b1a2b1⋮anb1a1b2a2b2⋮anb2⋯⋯⋱⋯a1bna2b2⋮anbn
再考虑这个问题的反面,即有没有二重求和是不能交换求和顺序的呢?
对于数值函数的二重积分,二重积分的值与积分次序无关要求积分区域既可表示成X-型区域,又可表示成Y-型区域。
对于二重求和而言,相当于对于一个矩形区域,变积分为求和。所以对于大多数情况而言,二重求和都是可以交换求和顺序的。(没有说得很绝对,因为这还仅仅是我自己的考虑,没有去考证)
相关文章:

矩阵1-范数与二重求和的求和可交换
矩阵1-范数与二重求和的求和可交换 1、矩阵1-范数 A [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] A \begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots …...

Python笔记 - *args和**kwargs
探索Python的*args和**kwargs 在Python中,函数可以接受任意数量的参数,而这要归功于*args和**kwargs的强大功能。这两个特性使得函数在处理不同数量的输入时变得更加灵活和高效。在这篇博客中,我们将详细介绍*args和**kwargs,并展…...

微信小程序实现图片转base64
在微信小程序中,图片转base63可以引入第三方插件; 也可以通过下边的方法转base64。 转换方法: imgToBase64(filePath) {return new Promise((resolve, reject) > {let baseFormat data:image/png;base64,let base64 wx.getFileSystem…...

os和os.path模块
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 目录也称文件夹,用于分层保存文件。通过目录可以分门别类地存放文件。我们也可以通过目录快速找到想要的文件。在Python中,并…...
链表题目练习----重排链表
这道题会联系到前面写的一篇文章----快慢指针相关经典问题。 重排链表 指针法 这道题乍一看,好像有点难处理,但如果仔细观察就会发现,这道题是查找中间节点反转链表链表的合并问题,具体细节有些不同,这个在反装中间链…...

【杂记-浅谈XSS跨站脚本攻击】
一、什么是XSS? XSS,Cross-site Scripting,跨站脚本攻击,是一种典型的Web程序漏洞利用攻击,攻击者利用Web程序对用户输入检查不足的漏洞将可执行恶意脚本注入网站或Web应用,当用户访问网页时触发恶意脚本的…...
VMware虚拟机与MobaXterm建立远程连接失败
VMware虚拟机与MobaXterm建立远程连接失败 首先可以检查一下是不是虚拟机的ssh服务并不存在 解决方法: 1.更新镜像源 yum -y update 这个过程会有点久,请耐心等待 2.安装ssh yum install openssh-server 3.启动ssh systemctl restart sshd 4.查…...

mysql undolog管理
在MySQL中,Undo Log(撤销日志)用于支持事务的回滚和MVCC(多版本并发控制)。为了避免Undo Log不断增长,影响系统性能,需要进行合理的清理。MySQL的Undo Log清理策略主要依赖于系统的配置参数和后…...

【Linux】进程2——管理概念,进程概念
1.什么是管理? 那在还没有学习进程之前,就问大家,操作系统是怎么管理进行进程管理的呢? 很简单,先把进程描述起来,再把进程组织起来! 我们拿大学为例子 最典型的管理者——校长最典型的被管理…...

【C++】植物大战僵尸杂交版自动存档——防闪退存档消失
植物大战僵尸杂交版现已更新到v2.0.88,闪退问题还是偶有发生,参考网上现有的方案,简单实现了一个。 原理就是监控存档目录的文件变化,一旦有新的存档,则将其备份。如发生闪退,则还原备份即可。 原目录&…...
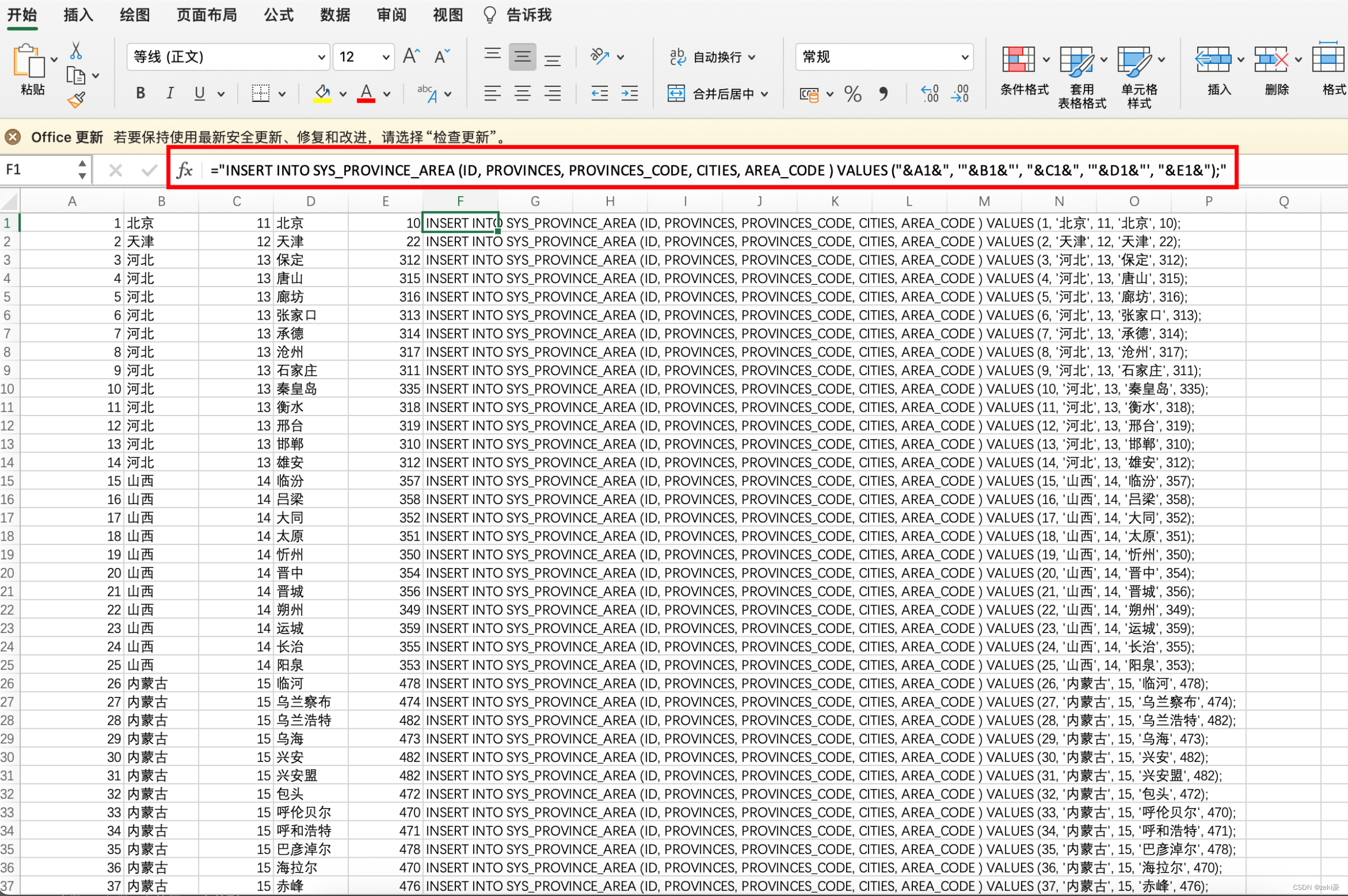
通过Excel,生成sql,将A表数据插入B表
文章目录 投机取巧的方式,进行表数据初始化通过navicat搜索A表数据,然后复制进excel中通过excel的函数方式,将该批量数据自动生成插入B表的sql语句然后一次性拷贝生成的sql语句,放进navicat中一次执行,直接完成数据初始化...

如何在MySQL中实现upsert:如果不存在则插入?
目录 1 使用 REPLACE 2 使用 INSERT ... ON DUPLICATE KEY UPDATE 使用 INSERT IGNORE 有效会导致 MySQL 在尝试执行语句时忽略执行错误 INSERT 。这意味着 包含 索引或 字段 INSERT IGNORE 中重复值的语句 不会 产生错误,而只是完全忽略该特定 命令。其明显目的是…...
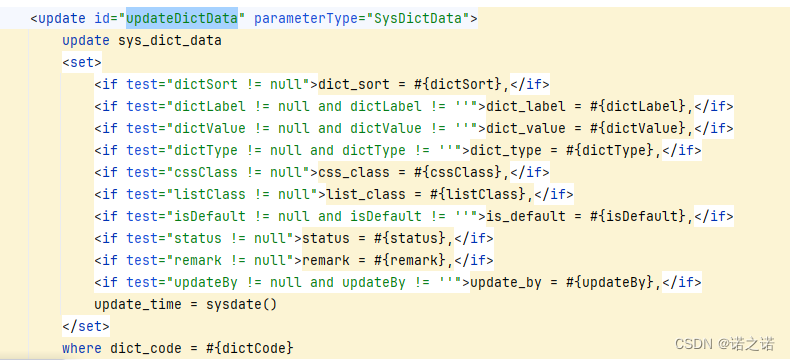
MyBatis中 set标签
1、set标签特点: set标签用于更新语句中set标签解析为set关键字set可以去除跟新语句中无用的逗号通常是和if标签一起使用 2、set标签的使用 编写接口方法编写sql语句 注意 当set标签中有条件成立时就会附加set关键字,字段为null时该列不会被更新。se…...

mysql自带分页
select 查询列表 from 表 limit offset,pagesize; offset代表的是起始的条目索引,默认从0开始size代表的是显示的条目数offset(n-1)*pagesize -- 第-页 limit 0 5 -- 第二页 limit 5,5 -- 第三页 limit 10,5 -- 第n页limit(n-1)*pagesize,pagesize -- pages…...

小学一年级数学上册,我终于学完了
目录 一、背景二、过程1.我对课程中的一些知识的思考2.我对于产品的思考3.我对自己儿子与知识产品结合的思考4.产品反馈的那些有意思的数据 三、总结 一、背景 简约而不简单,即是曾经的再现,也是未来的延伸,未来已来,就在脚下。 …...
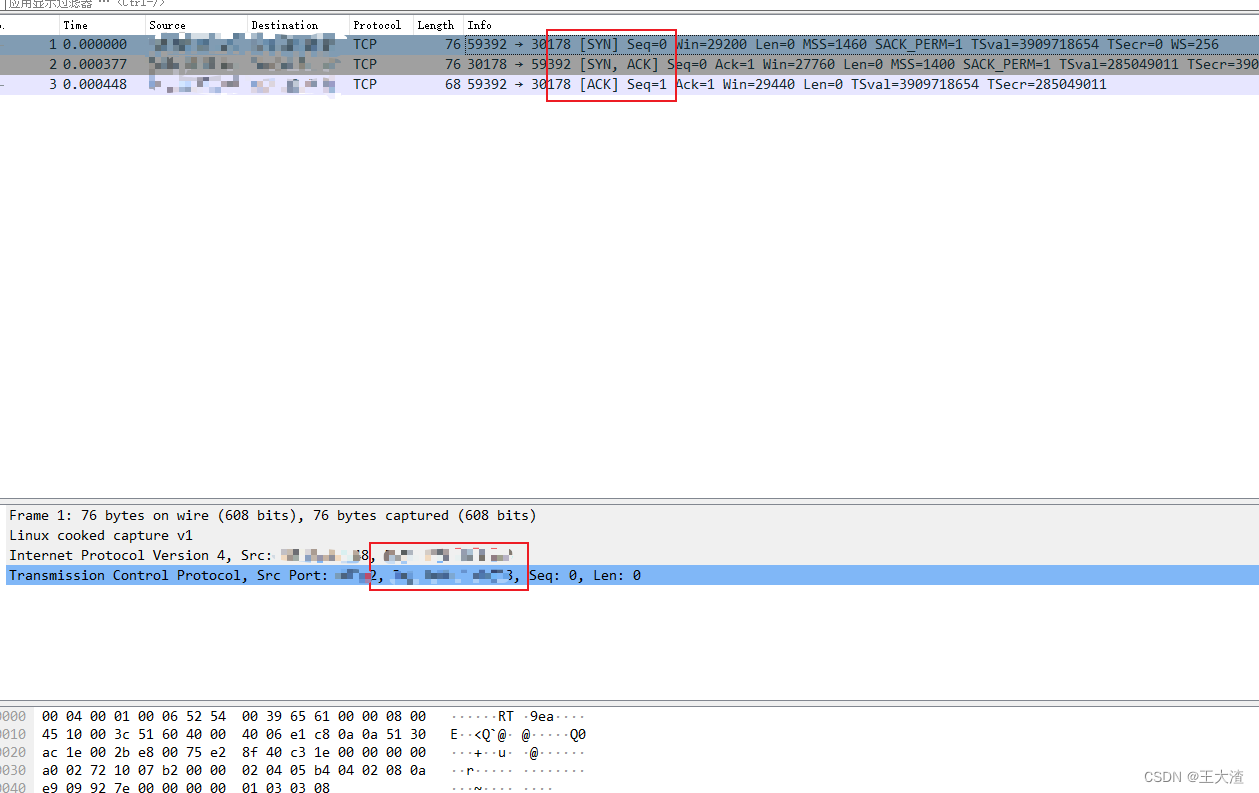
使用wireshark分析tcp握手过程
开启抓包 tcpdump -i any host 127.0.0.1 and port 123 -w tcp_capture.pcap 使用telnet模拟tcp连接 telnet 127.0.0.1 123 如果地址无法连接,则会一直重试SYN包,各个平台SYN重试间隔并不一致,如下: 异常站点抓包展示ÿ…...

在ArcGIS中,矢量数据有.shp,.mdb和.gdb,为啥建议使用gdb?
在ArcGIS中,矢量数据可以存储在多种格式中,如 .shp (Shapefile)、.mdb (Microsoft Access Database) 和 .gdb (Geodatabase)。每种格式都有其特定的用途和优缺点,但通常推荐使用 Geodatabase(.gdb)格式,原因如下: 1. 更高的数据容量和性能 容量: Shapefiles 和 MDB 文…...

C++STL---stack queue模拟实现
前言 对于这两个容器适配器的模拟实现非常简单,因为stack和queue只是对其他容器的接口进行了包装,在STL中,若我们不指明用哪种容器作为底层实现,栈和队列都默认是又deque作为底层实现的。 也就是说,stack和queue不管是…...
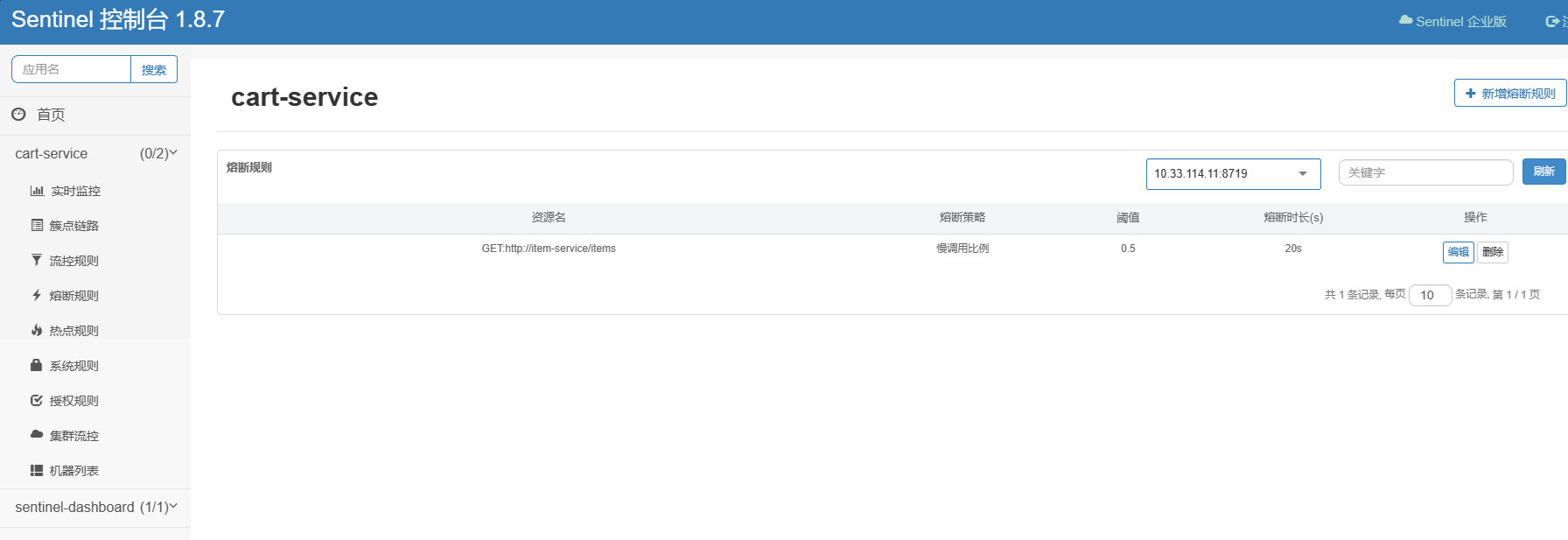
Spring Cloud系列——使用Sentinel进行微服务保护
文章目录 一、引言1. 雪崩问题的产生原因2. 解决雪崩问题的思路 二、微服务保护1. 服务保护方案1.1 请求限流1.2 线程隔离1.3 服务熔断 2. Sentinel2.1 安装2.2 微服务整合2.2.1 请求限流2.2.2 线程隔离①OpenFeign整合Sentinel②配置线程隔离 2.2.3 服务熔断①编写降级逻辑②配…...
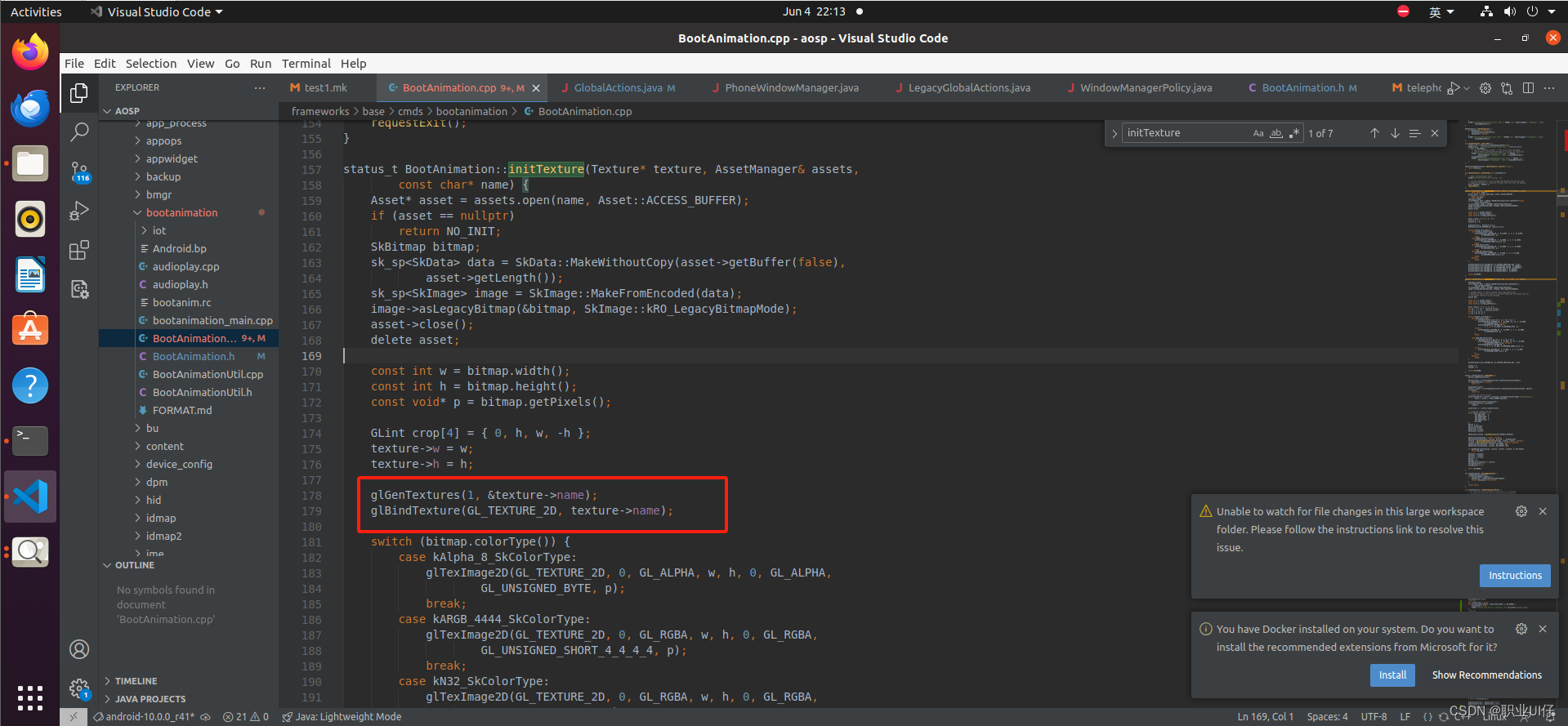
Android开机动画,framework修改Bootanimation绘制文字。
文章目录 Android开机动画,framework修改Bootanimation动画绘制文字。opengl绘制源码分析 Android开机动画,framework修改Bootanimation动画绘制文字。 frameworks/base/cmds/bootanimation/bootanimation.cpp 绘制时间的一个方法 // We render 12 or …...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
