LeetCode---二叉树
144/94/145. 二叉树的前、中、后序的递归遍历
以中序遍历为例,其余类似:
给定一个二叉树的根节点
root,返回 它的 中序 遍历 。

代码示例:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur,vector<int>& vec){if(cur == NULL) return;traversal(cur->left,vec);//左vec.push_back(cur->val);//中traversal(cur->right,vec);//右}vector<int> inorderTraversal(TreeNode* root) {vector<int> result;traversal(root,result);return result;}
};总结:不同的遍历方式只需将前中后三行代码交换顺序即可
递归三要素:
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
144/94/145. 二叉树的前、中、后序的非递归遍历(迭代)
1. 前序遍历和后续遍历:遍历节点和处理节点相同,可共用一套规则
2. 中序遍历:遍历节点和处理节点不相同
前序遍历:
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top(); // 中st.pop();result.push_back(node->val);if (node->right) st.push(node->right); // 右(空节点不入栈)if (node->left) st.push(node->left); // 左(空节点不入栈)}return result;}
};后序遍历:
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> result;if (root == NULL) return result;st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();result.push_back(node->val);if (node->left) st.push(node->left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)if (node->right) st.push(node->right); // 空节点不入栈}reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了return result;}
};
- 处理:将元素放进result数组中
- 访问:遍历节点
中序遍历:
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> result;stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点,访问到最底层st.push(cur); // 将访问的节点放进栈cur = cur->left; // 左} else {cur = st.top(); // 从栈里弹出的数据,就是要处理的数据(放进result数组里的数据)st.pop();result.push_back(cur->val); // 中cur = cur->right; // 右}}return result;}
};102. 二叉树的层序遍历
给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
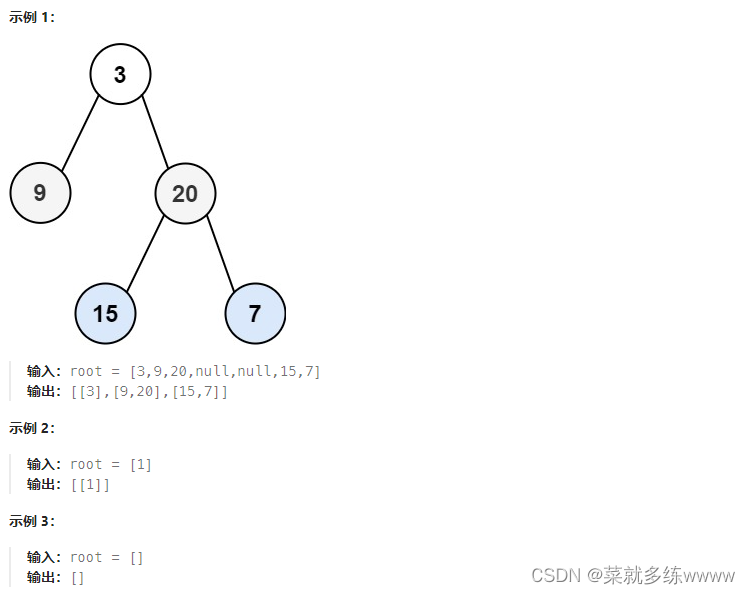
代码示例:
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;vector<vector<int>> result;if(root != NULL) que.push(root);while(!que.empty()){int size = que.size();vector<int> vec;while(size--){TreeNode* node = que.front();que.pop();vec.push_back(node->val);if(node->left) que.push(node->left);if(node->right) que.push(node->right);}result.push_back(vec);}return result;}
};107. 二叉树的层序遍历II
给你二叉树的根节点
root,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
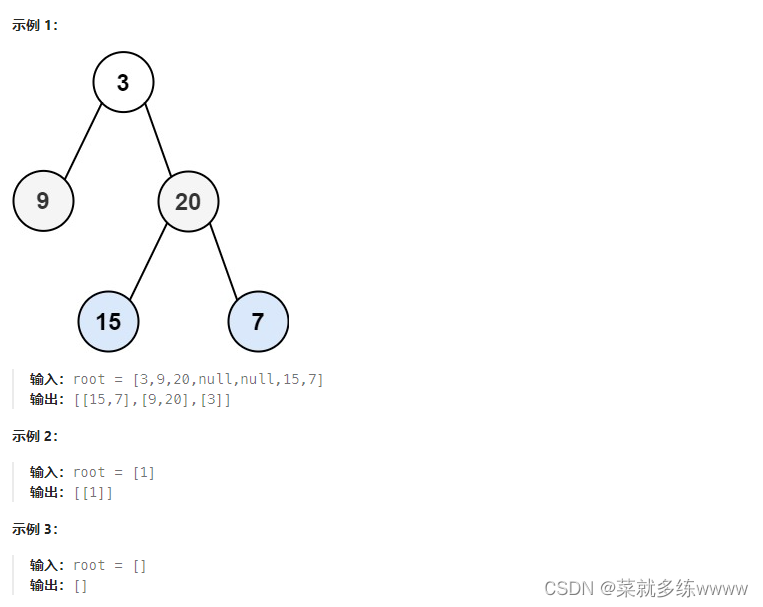
代码示例:
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {queue<TreeNode*> que;vector<vector<int>> result;if(root != NULL) que.push(root);while(!que.empty()){int size = que.size();vector<int> vec;while(size--){TreeNode* node = que.front();que.pop();vec.push_back(node->val);if(node->left) que.push(node->left);if(node->right) que.push(node->right);} result.push_back(vec);}reverse(result.begin(),result.end());return result;}
};注意:
以下写法是错的,因为
reverse函数不返回任何值(返回类型是void),它只是对输入范围内的元素进行原地修改。return reverse(result.begin(),result.end());
199. 二叉树的右视图
给定一个二叉树的 根节点
root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
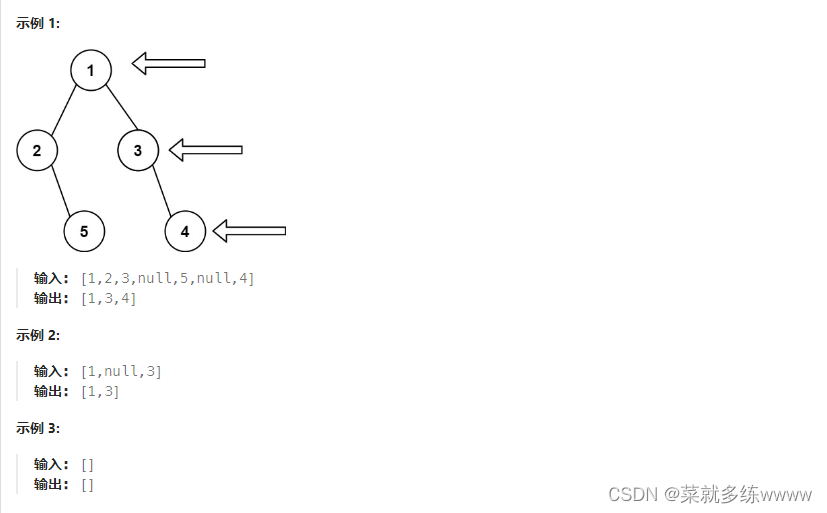
代码示例:
class Solution {
public:vector<int> rightSideView(TreeNode* root) {queue<TreeNode*> que;vector<int> result;if(root != NULL) que.push(root);while(!que.empty()){int size = que.size();for(int i = 0;i<size;i++){TreeNode* node = que.front();que.pop();if(i == (size - 1)) result.push_back(node->val);if(node->left) que.push(node->left);if(node->right) que.push(node->right);}} return result;}
};226. 翻转二叉树
给你一棵二叉树的根节点
root,翻转这棵二叉树,并返回其根节点。
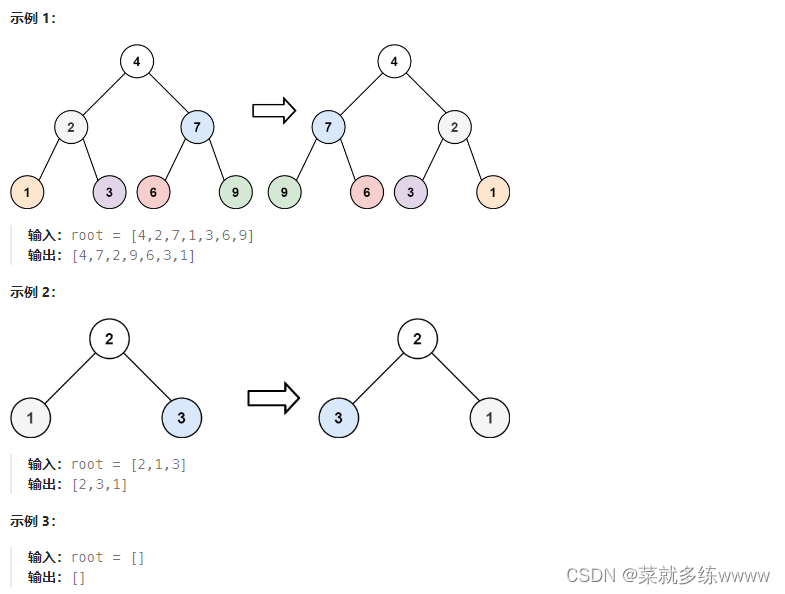
代码示例:
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;swap(root->left, root->right); // 中invertTree(root->left); // 左invertTree(root->right); // 右return root;}
};101. 对称二叉树
给你一个二叉树的根节点
root, 检查它是否轴对称。
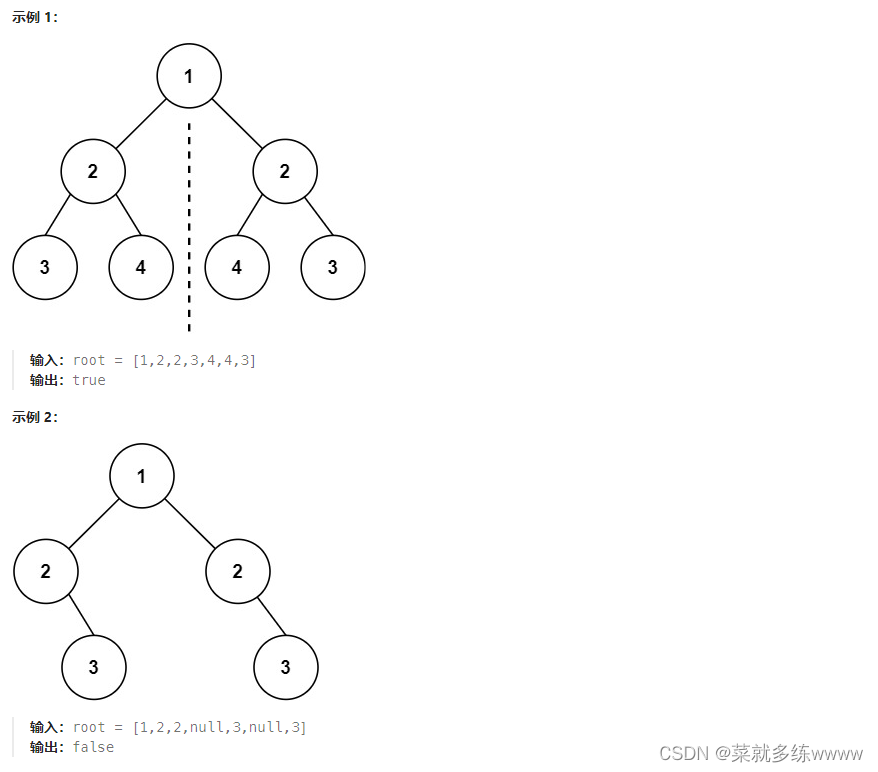
代码示例:
class Solution {
public:bool compare(TreeNode* left, TreeNode* right) {// 首先排除空节点的情况if (left == NULL && right != NULL) return false;else if (left != NULL && right == NULL) return false;else if (left == NULL && right == NULL) return true;// 排除了空节点,再排除数值不相同的情况else if (left->val != right->val) return false;// 此时就是:左右节点都不为空,且数值相同的情况// 此时才做递归,做下一层的判断bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)return isSame;}bool isSymmetric(TreeNode* root) {if (root == NULL) return true;return compare(root->left, root->right);}
};104. 二叉树的最大深度
给定一个二叉树
root,返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
二叉树的 最大高度 是指最从远叶子节点到根节点的最长路径上的节点数。
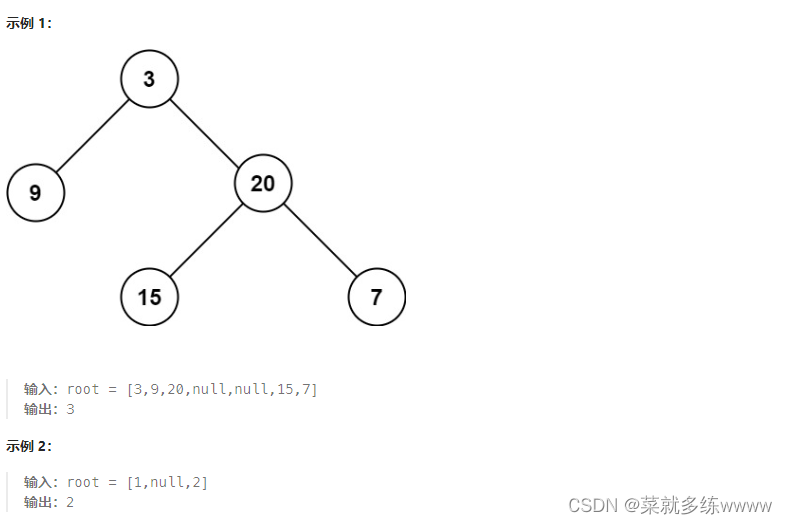
代码示例:
class Solution {
public:int getdepth(TreeNode* node) {if (node == NULL) return 0;int leftdepth = getdepth(node->left); // 左int rightdepth = getdepth(node->right); // 右int depth = 1 + max(leftdepth, rightdepth); // 中return depth;}int maxDepth(TreeNode* root) {return getdepth(root);}
};111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
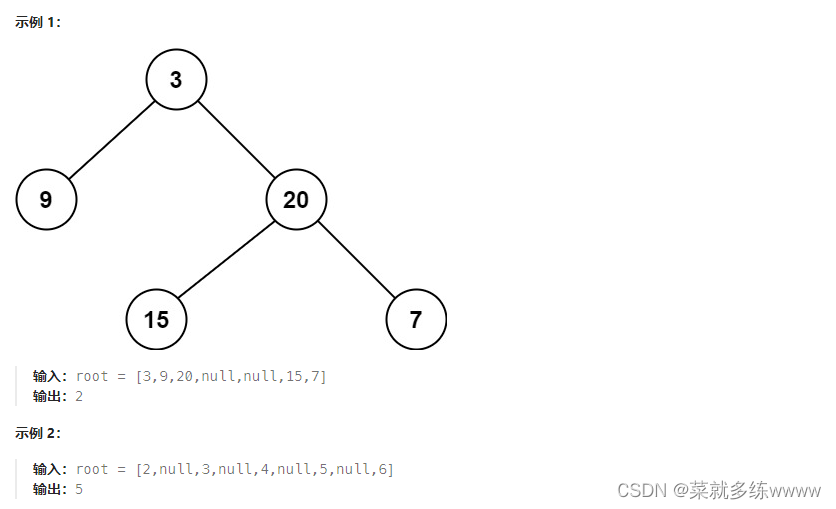
代码示例:
class Solution {
public:int getDepth(TreeNode* node) {if (node == NULL) return 0;int leftDepth = getDepth(node->left); // 左int rightDepth = getDepth(node->right); // 右// 中// 当一个左子树为空,右不为空,这时并不是最低点if (node->left == NULL && node->right != NULL) { return 1 + rightDepth;} // 当一个右子树为空,左不为空,这时并不是最低点if (node->left != NULL && node->right == NULL) { return 1 + leftDepth;}int result = 1 + min(leftDepth, rightDepth);return result;}int minDepth(TreeNode* root) {return getDepth(root);}
};222. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点
root,求出该树的节点个数。完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第
h层,则该层包含1~ 2h个节点。
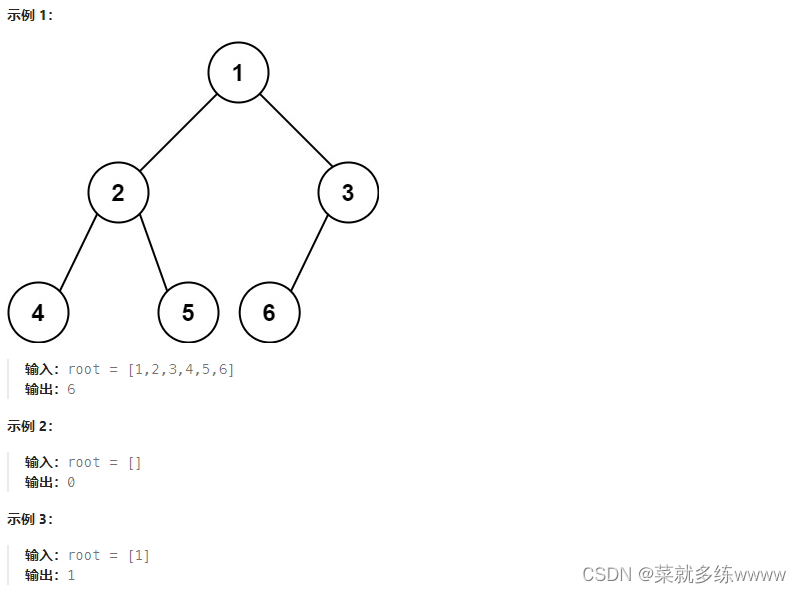
代码示例(普通二叉树解法):
class Solution {
private:int getNodesNum(TreeNode* cur) {if (cur == NULL) return 0;int leftNum = getNodesNum(cur->left); // 左int rightNum = getNodesNum(cur->right); // 右int treeNum = leftNum + rightNum + 1; // 中return treeNum;}
public:int countNodes(TreeNode* root) {return getNodesNum(root);}
};完全二叉树解法:
class Solution {
public:int countNodes(TreeNode* root) {if (root == nullptr) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便while (left) { // 求左子树深度left = left->left;leftDepth++;}while (right) { // 求右子树深度right = right->right;rightDepth++;}if (leftDepth == rightDepth) {return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0}return countNodes(root->left) + countNodes(root->right) + 1;}
};参考如下:
代码随想录
相关文章:

LeetCode---二叉树
144/94/145. 二叉树的前、中、后序的递归遍历 以中序遍历为例,其余类似: 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。 代码示例: /*** Definition for a binary tree node.* struct TreeNode {* int val;* Tr…...

从0开发一个Chrome插件:核心功能开发——弹出页面
前言 这是《从0开发一个Chrome插件》系列的第十一篇文章,本系列教你如何从0去开发一个Chrome插件,每篇文章都会好好打磨,写清楚我在开发过程遇到的问题,还有开发经验和技巧。 专栏: 从0开发一个Chrome插件:什么是Chrome插件?从0开发一个Chrome插件:开发Chrome插件的必…...

AIGC笔记--Stable Diffusion源码剖析之UNetModel
1--前言 以论文《High-Resolution Image Synthesis with Latent Diffusion Models》 开源的项目为例,剖析Stable Diffusion经典组成部分,巩固学习加深印象。 2--UNetModel 一个可以debug的小demo:SD_UNet 以文生图为例&#…...

Linux文件系统与日志分析
目录 inode block 链接 文件修复 实验步骤 针对ext文件系统恢复删除文件 针对xfs文件系统恢复删除文件 日志 日志级别 rsyslogd服务 日志目录 messages日志文件(系统日志) 集中管理日志 - 实验 1.环境配置 1.1 1.2 1.3 1.4 1.5 2.远…...
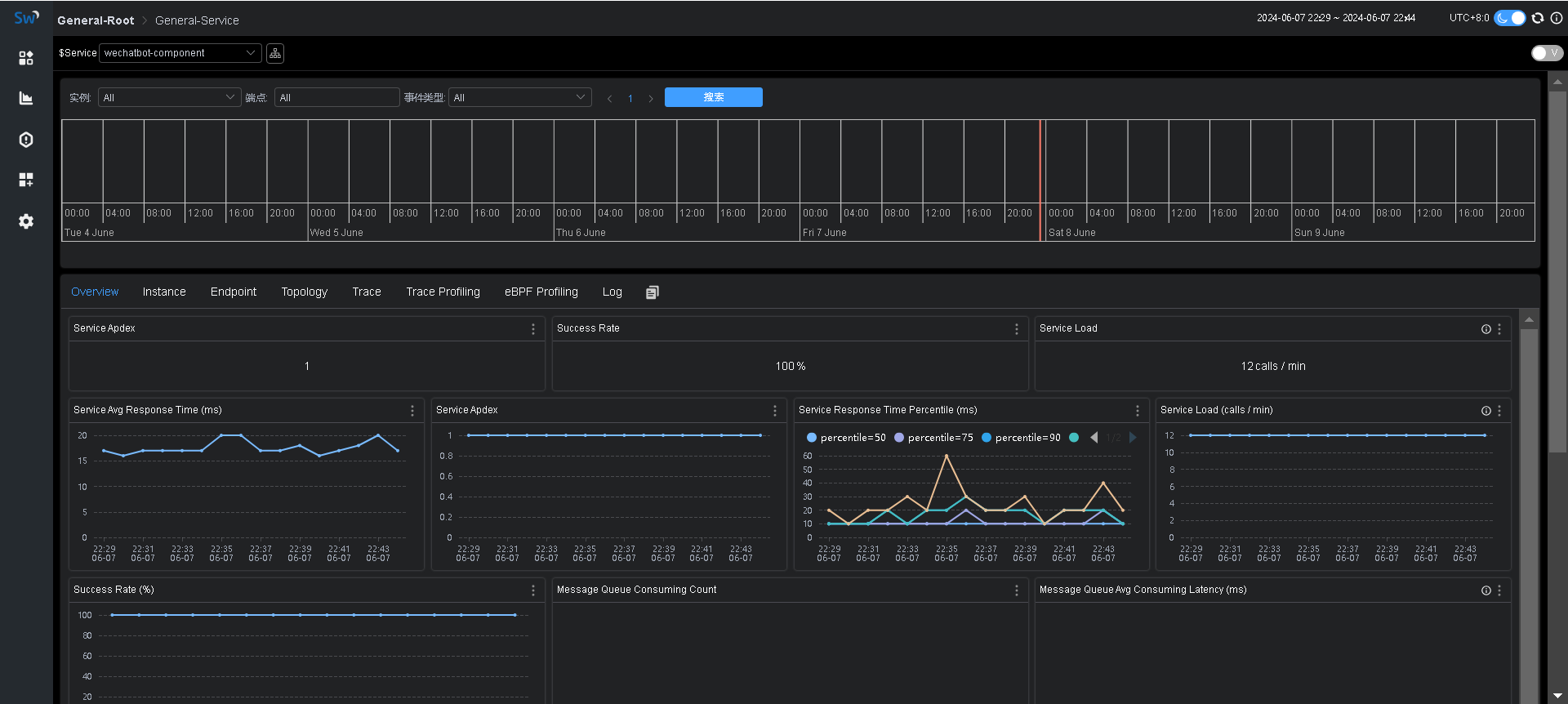
【SkyWalking】使用PostgreSQL做存储K8s部署
拉取镜像 docker pull apache/skywalking-ui:10.0.1 docker tag apache/skywalking-ui:10.0.1 xxx/xxx/skywalking-ui:10.0.1 docker push xxx/xxx/skywalking-ui:10.0.1docker pull apache/skywalking-oap-server:10.0.1 docker tag apache/skywalking-oap-server:10.0.1 xxx…...

详解大模型微调数据集构建方法(持续更新)
大家好,我是herosunly。985院校硕士毕业,现担任算法t研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算…...

自制植物大战僵尸:HTML5与JavaScript实现的简单游戏
引言 在本文中,我们将一起探索如何使用HTML5和JavaScript来创建一个简单的植物大战僵尸游戏。这不仅是一项有趣的编程挑战,也是学习游戏开发基础的绝佳机会。 什么是植物大战僵尸? 植物大战僵尸是一款流行的策略塔防游戏,玩家需…...
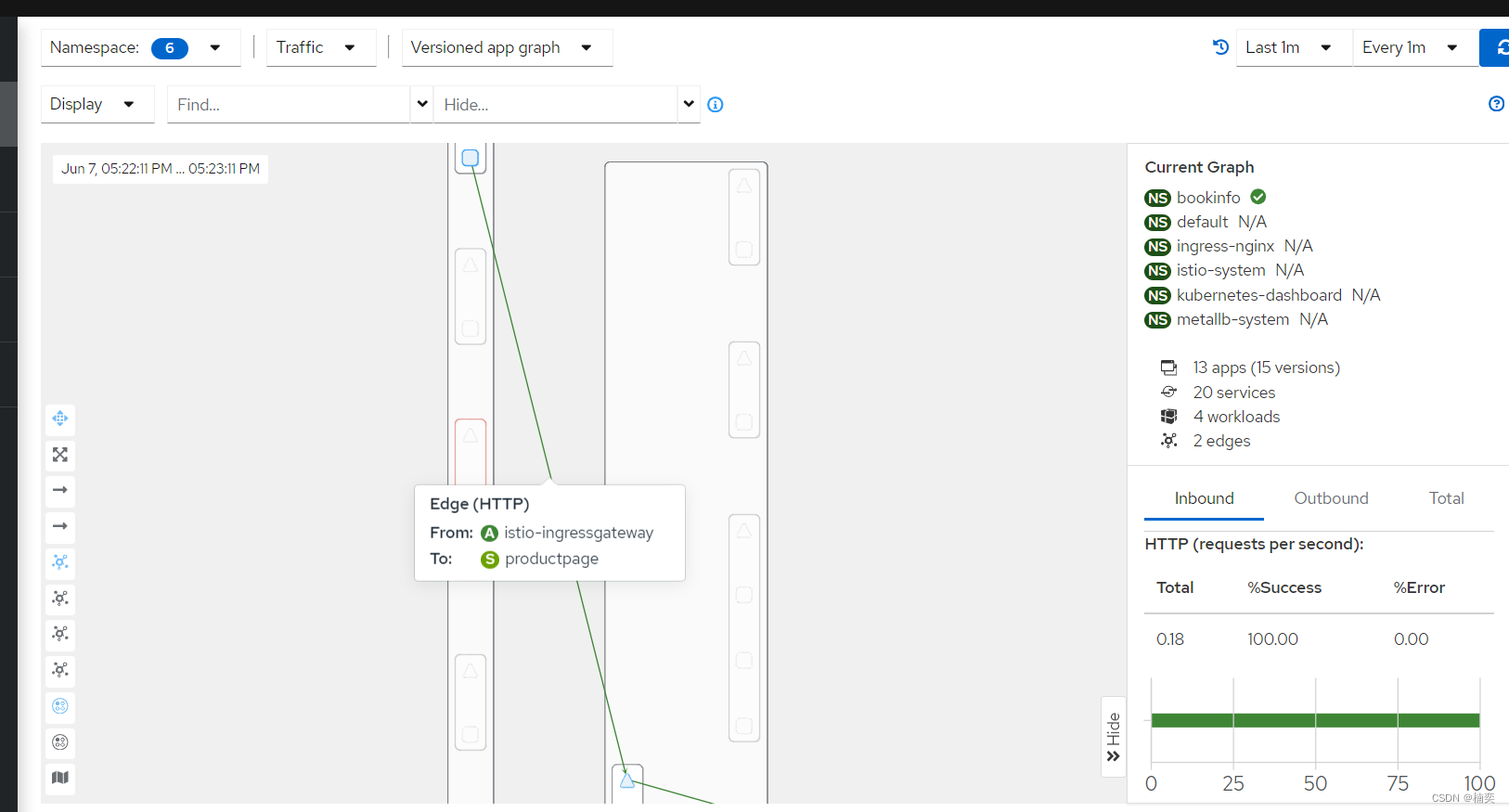
Istio_1.17.8安装
项目背景 按照istio官网的命令一路安装下来,安装好的istio版本为目前的最新版本,1.22.0。而我的k8s集群的版本并不支持istio_1.22的版本,导致ingress-gate网关安装不上,再仔细查看istio的发布文档,如果用istio_1.22版本…...
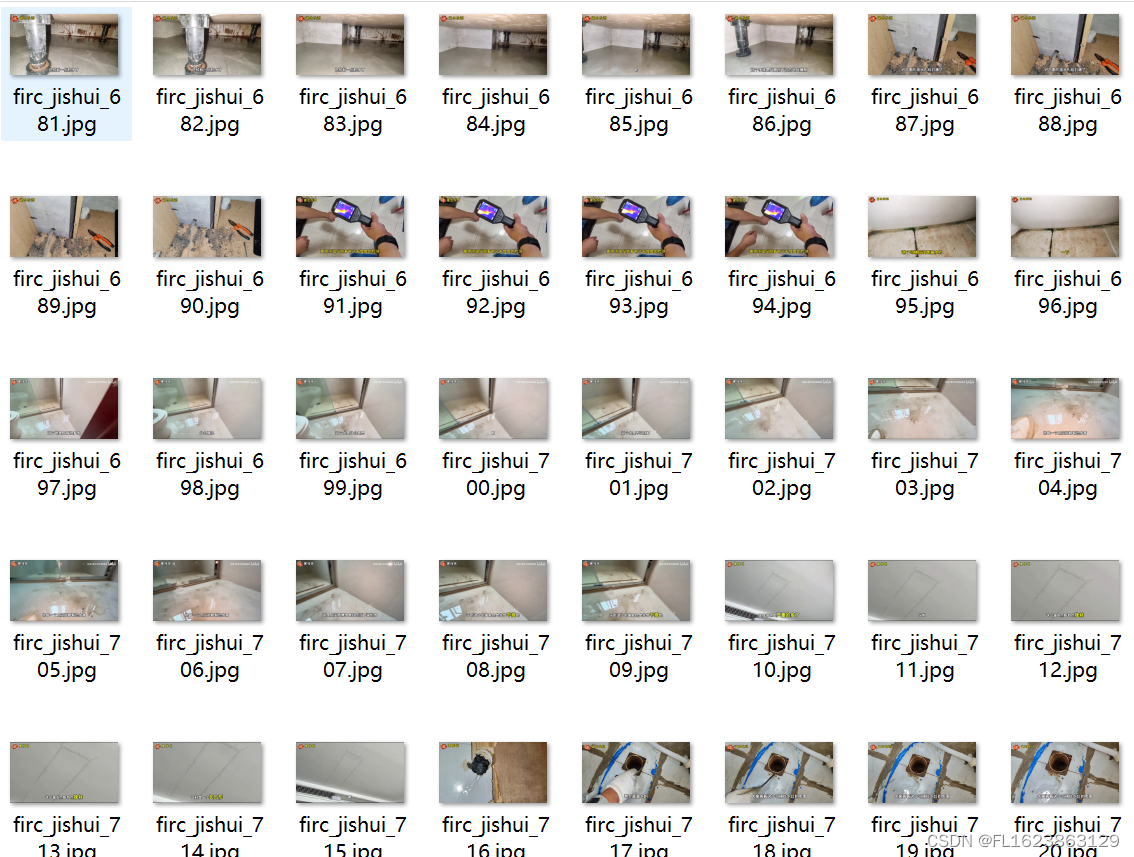
[数据集][目标检测]室内积水检测数据集VOC+YOLO格式761张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):761 标注数量(xml文件个数):761 标注数量(txt文件个数):761 标注类别…...
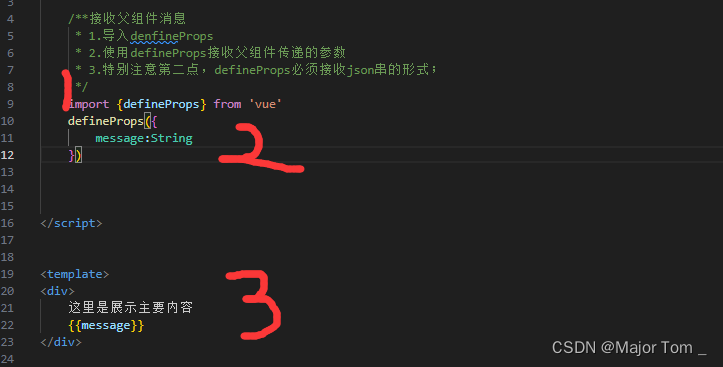
17_Vue高级监听器生命周期Vue组件组件通信
文章目录 1. 数据监听器watch2. Vue生命周期3. Vue组件4. Vue组件通信Appendix 1. 数据监听器watch 首先watch需要单独引 import {watch} from vuewatch函数监听ref响应式数据 watch(监听的内容,监听行为)监听行为默认为(newValue,oldValue) let firstname ref…...
【ROS使用记录】—— ros使用过程中的rosbag录制播放和ros话题信息相关的指令与操作记录
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、rosbag的介绍二、rosbag的在线和离线录制三、rosbag的播放相关的指令四、其他rosbag和ros话题相关的指令总结 前言 rosbag是ROS(机器人操作系统…...

Laravel 富文本内容
Laravel 获取富文本的纯文本内容-CSDN博客 Laravel 富文本内容里面的图片添加前缀URL-CSDN博客 Laravel 富文本图片的style样式删除-CSDN博客. Laravel 获取富文本中的所有图片-CSDN博客 富文本字体font-famly删除 $data preg_replace(/(<[^>])style["\][^"…...

Spark Python环境搭建与优化:深入剖析四个方面、五个方面、六个方面及七个关键要点
Spark Python环境搭建与优化:深入剖析四个方面、五个方面、六个方面及七个关键要点 在大数据处理领域,Apache Spark凭借其出色的性能和灵活性备受瞩目。而要在Python中利用Spark的强大功能,首先需要搭建一个稳定且高效的Spark Python环境。本…...
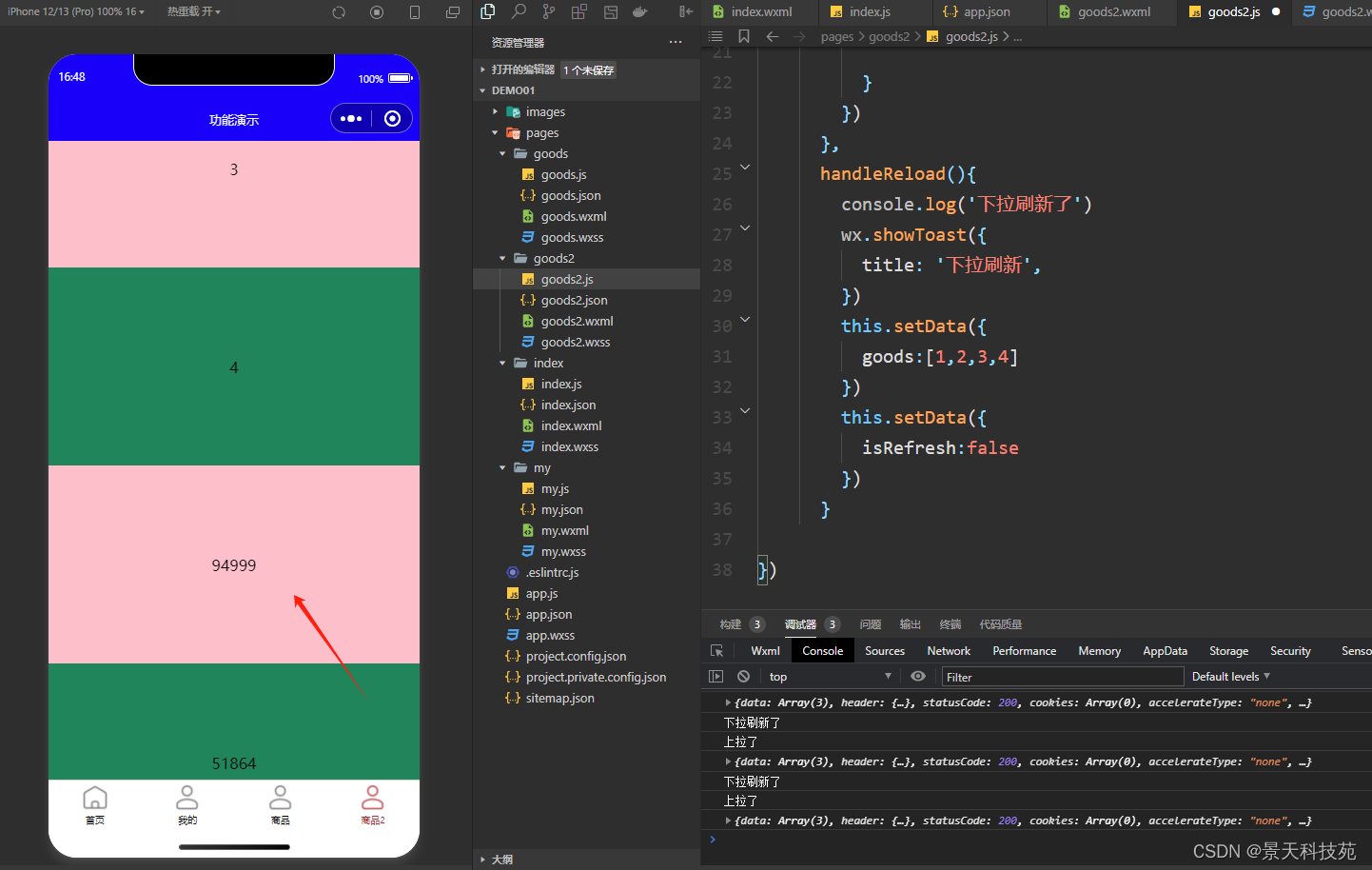
【微信小程序开发】小程序中的上滑加载更多,下拉刷新是如何实现的?
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

从 Android 恢复已删除的备份录
本文介绍了几种在 Android 上恢复丢失和删除的短信的方法。这些方法都不能保证一定成功,但您可能能够恢复一些短信或其中存储的文件。 首先要尝试什么 首先,尝试保留数据。如果你刚刚删除了信息,请立即将手机置于飞行模式,方法是…...

如何使用Python中的random模块生成随机数
在Python中,random模块提供了多种用于生成随机数的函数。以下是一些基本示例: 生成随机整数: 使用random.randint(a, b)函数生成一个介于a和b之间的随机整数(包括a和b)。 python复制代码 import random random_int …...
AI大数据处理与分析实战--体育问卷分析
AI大数据处理与分析实战–体育问卷分析 前言:前一段时间接了一个需求,使用AI进行数据分析与处理,遂整理了一下大致过程和大致简要结果(更详细就不方便放了)。 文章目录 AI大数据处理与分析实战--体育问卷分析一、数据…...

C++第二十五弹---从零开始模拟STL中的list(下)
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1、函数补充 2、迭代器完善 3、const迭代器 总结 1、函数补充 拷贝构造 思路: 先构造一个头结点,然后将 lt 类中的元…...

STM32/keil把多个c文件编译为静态库lib
把常用的、不经常修改的代码库编译成lib以后,可以加快整个工程的编译速度。 一个常见的应用场景就是,把ST的标准库或HAL库等编译成lib,这样以后再编译整个工程时,就无需再次编译他们了,可以节省编译时间。当然&#x…...

L45---506.相对名次(java)--排序
1.题目描述 2.知识点 (1)String.join(" ", words) 是 Java 中的一个语法,用于将数组或集合中的元素连接成一个单独的字符串,连接时使用指定的分隔符。这里的 " " 是作为分隔符使用的一个空格字符串。 Strin…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
