异步复位和同步释放
文章目录
- 前言
- 一、为什么需要复位呢?
- 二、同步复位
- 1. 同步复位定义
- 2. 同步复位的实现
- 3. 同步复位的优点和缺点
- 同步复位优点
- 同步复位缺点
- 三、异步复位
- 1. 异步复位定义
- 2. 异步复位的实现
- 3. 异步复位的优点和缺点
- 异步复位优点
- 异步复位缺点
- 四、异步复位同步释放
- 1. recovery time和removal time
- 2. 异步复位同步释放的含义
- 3. 异步复位同步释放的实现
- 4. 异步复位同步释放优点
- 总结
前言
复位信号在数字电路里面的重要性仅次于时钟信号。对一个芯片来说,复位的主要目的是使芯片电路进入一个已知的,确定的状态,主要是触发器进入确定的状态。在一般情况下,芯片中的每个触发器都应该是可复位的。
一、为什么需要复位呢?
- 复位可以使电路从确定的初始状态开始运行
比如上电复位,上电的时候,为了避免上电后进入随机状态而使电路紊乱,这个时候就需要上电复位。时序电路是一个双稳态电路,上电之后必须要有一个初始态,才可以正常运行。组合逻辑电路,没有存储功能,不需要复位信号。 - 复位可以使电路从错误状态回到可以控制的确定状态
如果电路发生了异常,比如状态不正常,中断异常,firmware程序跑飞,这个时候就可以对电路进行复位,让它从错误的状态回到一个正常的状态。 - 电路仿真时需要电路具有已知的初始值
在仿真的时候,信号在初始状态是未知状态(也就是所谓的x,不过对信号初始化之后的这种情况除外,因为仿真的时候对信号初始化就使信号有了初始值,这就不是x了)。仿真的时候由于初始状态为未知态,控制电路一开始就陷入了未知态。仿真跟实际电路不同,仿真是“串行”的,仿真时控制信号的初始不定态会导致后续的控制信号结果都是不定态,也就是说,初始的不定态对控制通道是致命的。
二、同步复位
1. 同步复位定义
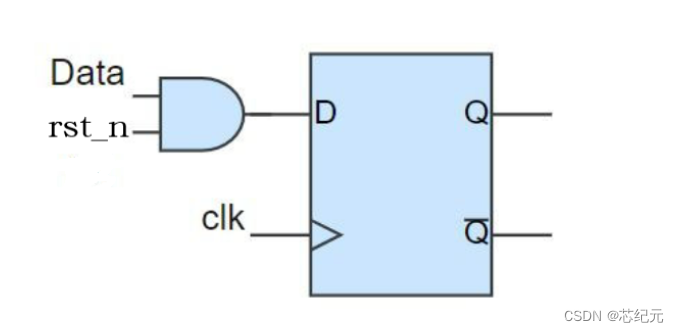
同步复位的前提是,复位信号只会在时钟的有效边沿去影响或者复位flip-flop。Reset可以作为组合逻辑的一部分送给FF的D端。这种情况下,reset只能放在if条件下。
2. 同步复位的实现
一个简单的同步复位的D触发器代码如下(示例):
module sync_reset_dff_module (input clk,input rst_n, // Synchronous resetinput d,output reg q);always @ (posedge clk)if (!rst_n) q <= 1'b0;else q <= d;
endmodule
3. 同步复位的优点和缺点
同步复位优点
1). 同步复位会综合成更小的触发器,特别当reset生成逻辑电路作为触发器D输入,但是这种情况下组合逻辑电路的数量变多,所以总的门电路节省不是那么显著;
2). 同步复位确保电路100%是同步的, 有利于静态时序分析工具的分析;
3). 抗干扰性高,同步复位确保复位只发生在时钟有效边沿,对小的复位毛刺来说,时钟就像滤波器。
同步复位缺点
1). 大多数逻辑器件的目标库内的DFF都只有异步复位端口,使用同步复位时,综合器就会在寄存器的数据输入端插入组合逻辑,占用更多的逻辑资源;
2). 同步复位依赖于时钟,如果电路中的时钟信号出现问题,无法完成复位;
3). 对复位信号的脉冲宽度有要求,必须大于指定的时钟周期,由于线路上的延迟,可能需要多个时钟周期的复位脉冲宽度,且很难保证复位信号到达各个寄存器的时序。
三、异步复位
1. 异步复位定义
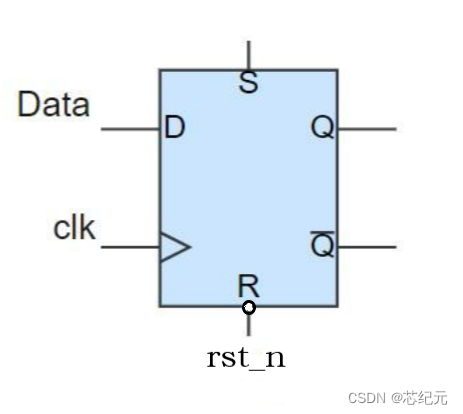
异步复位电路即复位信号不随着系统时钟的边沿触发起作用。拥有异步复位的寄存器在设计过程中就多了一个引脚(复位引脚)。
2. 异步复位的实现
一个简单的异步复位的D触发器代码如下(示例):
module async_reset_dff_module (input clk,input rst_n, // Synchronous resetinput d,output reg q);always @ (posedge clk or negedge rst_n)if (!rst_n) q <= 1'b0;else q <= d;
endmodule
3. 异步复位的优点和缺点
异步复位优点
1). 由于大多数的厂商标准单元库内的触发器都有异步复位端口,那么就可以保证数据路径是干净的,不会像同步复位一样插入额外的逻辑,可以节约逻辑资源;
2). 复位信号不依赖于时钟。
异步复位缺点
1). 复位信号容易受到毛刺的影响;
2). 当复位结束时刻恰在亚稳态窗口内时,无法决定现在的复位状态是1还是0,会导致亚稳态。
四、异步复位同步释放
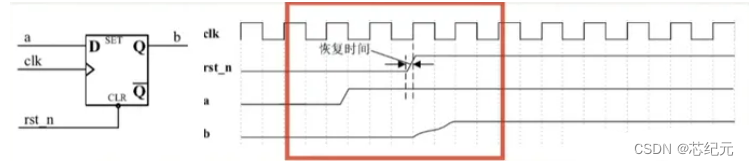
1. recovery time和removal time
在同步电路中,输入数据需要与时钟满足setup time和hold time才能进行数据的正常传输,防止亚稳态。同样的道理,对于一个异步复位寄存器来说,异步复位信号同样需要和时钟满足recovery time和removal time 才能有效进行复位操作和复位释放操作,防止输出亚稳态。
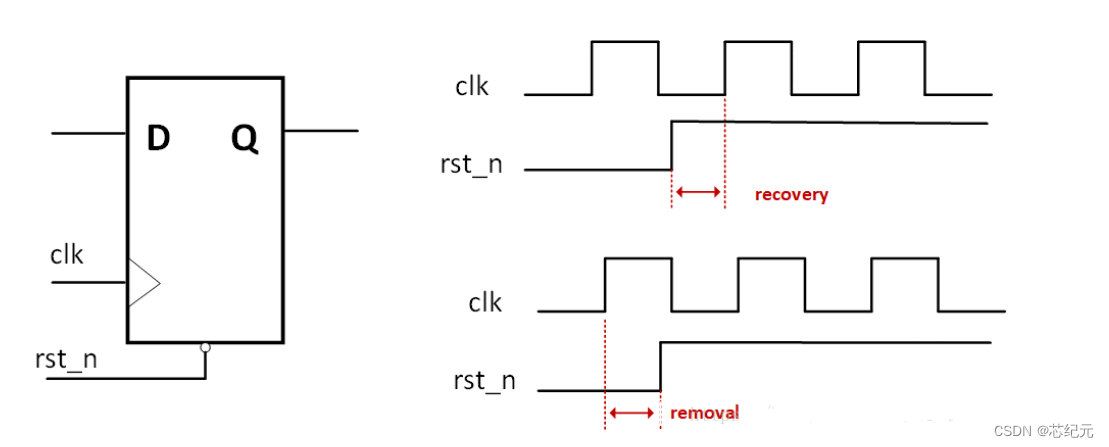
recovery time(恢复时间):撤销复位时,恢复到非复位状态的电平必须在时钟有效沿来临之前的一段时间到来,才能保证时钟能有效恢复到非复位状态,此段时间为recovery time即复位释放与下一个时钟有效边沿之间需要间隔的最小时间,类似于同步时钟的setup time。
removal time (去除时间):复位时,在时钟有效沿来临之后复位信号还需要保持复位状态的一段时间为去除时间removal time即复位释放与上一个时钟有效边沿之间需要间隔的最小时间。类似同步时钟hold time。
异步复位信号一般会持续相对较长的时间,保证寄存器能复位完成。但是由于复位信号是异步的,我们不知道它会在什么时刻被释放。如果异步复位信号撤销时,不满足recovery time和removal time时,可能会造成亚稳态,因为复位信号还没完全取消时触发器发现自己该采样了,最终导致输出有可能是复位值0也有可能是采样到的D端的值,输出不确定。
另外,并不是复位信号撤销时才可能出现亚稳态,复位信号一开始出现时,同样可能会存在亚稳态,只不过异步复位信号持续时间长,即使第一个周期出现了亚稳态(即第一个周期复位未成功),下一个时钟周期也不会再出现亚稳态了。如果复位信号的变化只持续刚刚一个时钟周期,那么复位信号开始和撤销时都可能会出现亚稳态。
2. 异步复位同步释放的含义
所谓异步复位同步释放(Synchronized Asynchronous Reset),就是在复位信号到来的时候不受时钟信号的同步,而是在复位信号释放的时候受到时钟信号的同步。
电路目的:防止复位信号撤除时产生亚稳态事件。
异步复位:显而易见,reset_n异步复位后,rst_n将拉低,即实现异步复位。
同步释放:这个是关键,看如何实现同步释放,即当复位信号reset_n撤除时,由于双缓冲电路(双寄存器)的作用,rst_n复位信号不会随着reset_n的撤除而撤除。
3. 异步复位同步释放的实现
一个简单的异步信号同步化代码如下(示例):
//Synchronized Asynchronous Reset
module sync_async_reset (input clk,input rst_async_n,output reg rst_sync_n
);
reg rst_s1;
always @(posedge clk or negedge rst_async_n)
beginif(!rst_async_n) beginrst_s1 <= 1'b0;rst_sync_n <= 1'b0;endelse beginrst_s1 <= 1'b1;rst_sync_n <= rst_s1;end
end
endmodule
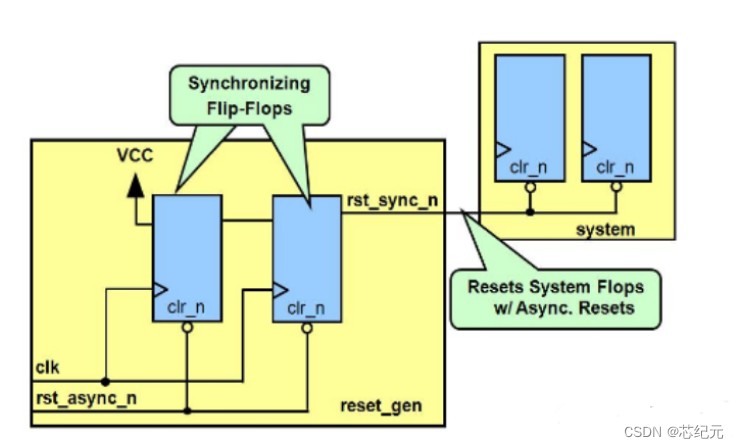
当异步复位信号撤销时,用来同步的第二个寄存器输入的数据仍然是0,因此第二个寄存器是不会出现亚稳态的。第一个寄存器虽然可能出现亚稳态,即使其出现了亚稳态,这个亚稳态还需要通过第二个寄存器,这时第二个寄存器就起到了打拍的作用。也就是说,第二级的亚稳态只可能是上一级寄存器传播过来的,但是这个亚稳态经过第二级寄存器后,其大概率已经稳定下来了,就算稳定下来不为1,也就相当与复位信号多持续了一个周期而已。因此我们可以看出,使用异步复位同步释放时,异步复位撤销后需要额外等待一个时钟周期。
4. 异步复位同步释放优点
异步复位同步释放既解决了同步复位的资源消耗问题,又解决了异步复位的亚稳态问题,其根本思想是异步信号同步化。
总结
不同的复位方式有各自的优缺点。但是在工程中,一般都用异步复位的方法,最好是异步复位同步释放的方法。
相关文章:

异步复位和同步释放
文章目录 前言一、为什么需要复位呢?二、同步复位1. 同步复位定义2. 同步复位的实现3. 同步复位的优点和缺点同步复位优点同步复位缺点 三、异步复位1. 异步复位定义2. 异步复位的实现3. 异步复位的优点和缺点异步复位优点异步复位缺点 四、异步复位同步释放1. reco…...

03-3.2.4 双端队列
👋 Hi, I’m Beast Cheng👀 I’m interested in photography, hiking, landscape…🌱 I’m currently learning python, javascript, kotlin…📫 How to reach me --> 458290771qq.com 喜欢《数据结构》部分笔记的小伙伴可以订…...
SpringBoot的Mapper文件什么时候需要使用@Param注解
解决:nested exception is org.apache.ibatis.binding.BindingException: Parameter ‘XXX‘ not found 关于加注解,其他博客说的很清楚!但是有的人会遇见明明使用的springboot2.x以上版本,仍然提示需要加注解!这是为…...

2024.6.8
2024.6.8 **每日一题** 3040.相同分数的最大操作数目 Ⅱ,通多题意可知,该题最多有三种操作分数,分别是前两个,最后两个,以及第一个和最后一个的和。从这里也可以看出一共有三种状态转移方式,所以我们可以利…...
室内外融合定位是如何做到成为定位领域的新宠
在信息化高速发展的今天,定位技术已成为人们生活和工作中不可或缺的一部分。随着物联网、智慧城市等领域的蓬勃发展,传统的单一定位方式已无法满足复杂多变的环境需求。在这样的背景下,室内外融合定位技术应运而生,以其独特的优势…...

【刷题篇】分治-归并排序
文章目录 1、排序数组2、交易逆序对的总数3、计算右侧小于当前元素的个数4、翻转对 1、排序数组 给你一个整数数组 nums,请你将该数组升序排列。 class Solution { public:vector<int> tmp;void mergeSort(vector<int>& nums,int left,int right){…...
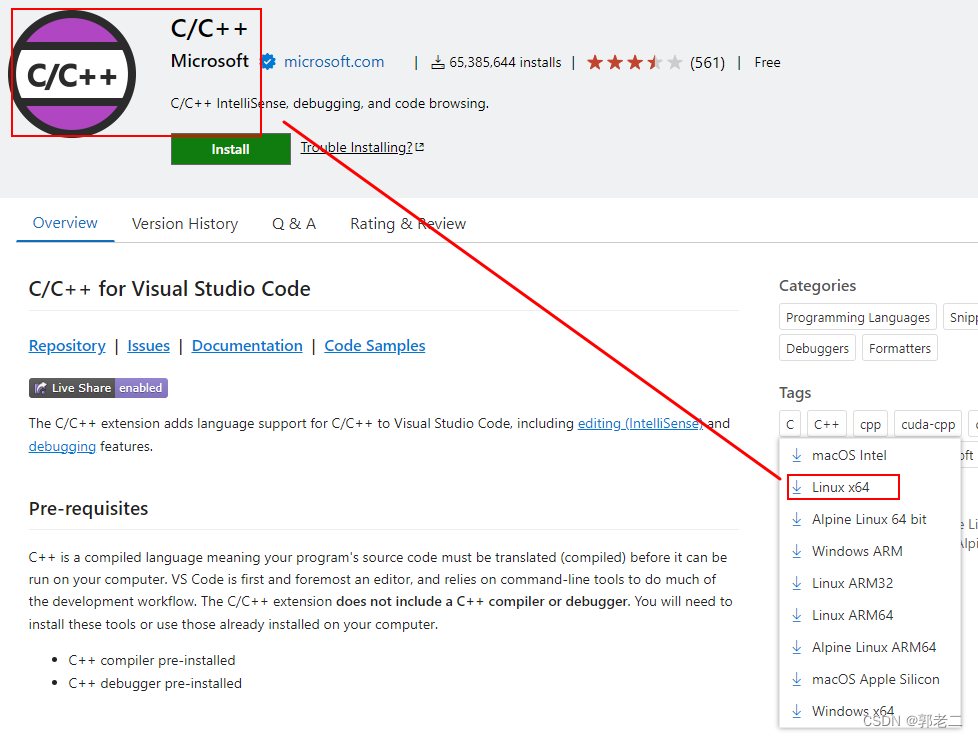
【经验】Ubuntu上离线安装VsCode插件浏览Linux kernel源码
1、下载VsCode离线安装包 1.1 下载 下载地址:https://marketplace.visualstudio.com/vscode 本人安装的插件: C/C++ checkpatch Chinese clangd kconfig Makefile Tools Perl Perl Toolbox注意:C/C++插件要安装Linux 64版本 1.2 安装 将离线安装包拷贝到Ubuntu中,执…...

鼠标侧键映射虚拟桌面切换 —— Win11
鼠标侧键映射虚拟桌面切换 —— Win11 基于 AutoHotkey 实现功能 下载软件 AutoHotkey建议安装在默认路径下(C盘) 此软件非常小,几乎不占用资源软件安装在默认路径以外的位置可能导致部分功能不可用 新建一个 .ahk 文件使用记事本打开该 .a…...

2024全国大学生数据统计与分析竞赛B题【电信银行卡诈骗的数据分析】思路详解
电信诈骗是指通过电话、网络和短信方式,编造虚假信息,设置骗局,对受害人实施远程、非接触式诈骗,诱使受害人打款或转账的犯罪行为,通常以冒充他人及仿冒、伪造各种合法外衣和形式的方式达到欺骗的目的,如冒…...

鸿蒙emitter 订阅事件封装 EmitterUtils
适用于api11 和api12 废话不多说,直接上代码 import emitter from ohos.events.emitter; import { StringUtils } from ohos/flutter_ohos;export class EmitterUtils{/*** 发射字符串类型的* param eventId* param data*/public static sendEvent(eventId:stri…...
)
C语言---深入指针(4)
回调函数 //回调函数就是通过函数指针调用的函数 //这个在之前的转移表-计算器里面很明显,通过函数指针数组内的函数指针进行函数的调用 // // // 将这四段代码分装成一个函数,一个代码将这4个问题都解决 int Add(int x, int y) {return x y; } int S…...
【启程Golang之旅】让文件操作变得简单
欢迎来到Golang的世界!在当今快节奏的软件开发领域,选择一种高效、简洁的编程语言至关重要。而在这方面,Golang(又称Go)无疑是一个备受瞩目的选择。在本文中,带领您探索Golang的世界,一步步地了…...

oracle视图无法删除,orcl视图删除卡住怎么办
话说,这是一个来自周四加班夜晚的故事,当时我的PL/SQL卡住了,每次查询这个表时都会卡住。 经过一番研究,我找到了解决办法,分为三个步骤: 使用以下查询语句获取正在执行的SQL查询的SID和OracleID…...

ug编程怎么录制宏:一步步探索自动化编程的奥秘
ug编程怎么录制宏:一步步探索自动化编程的奥秘 在UG编程的浩瀚领域中,录制宏是一项强大而神秘的功能。它就像一位魔法师,能够将繁琐的重复操作化为简单的指令,释放出惊人的编程效率。然而,对于许多初学者来说…...
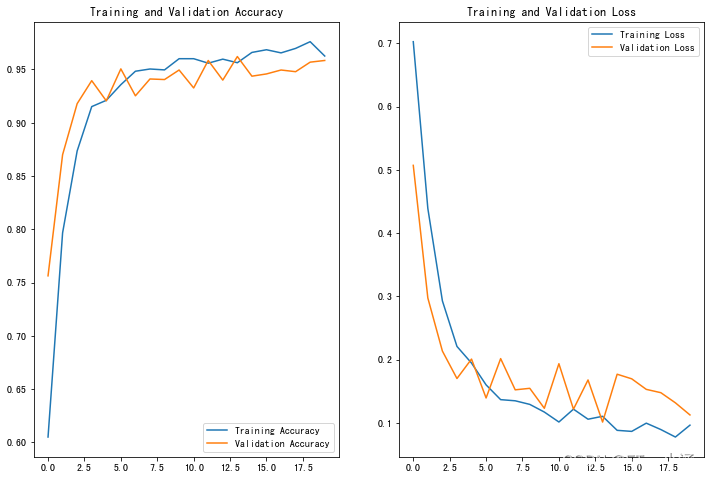
深度学习Week16——数据增强
文章目录 深度学习Week16——数据增强 一、前言 二、我的环境 三、前期工作 1、配置环境 2、导入数据 2.1 加载数据 2.2 配置数据集 2.3 数据可视化 四、数据增强 五、增强方式 1、将其嵌入model中 2、在Dataset数据集中进行数据增强 六、训练模型 七、自定义增强函数 一、前言…...

python-自幂数判断
[题目描述]: 自幂数是指,一个N 位数,满足各位数字N 次方之和是本身。例如,153153 是 33 位数,其每位数的 33 次方之和,135333153135333153,因此 153153 是自幂数;16341634 是 44 位数…...
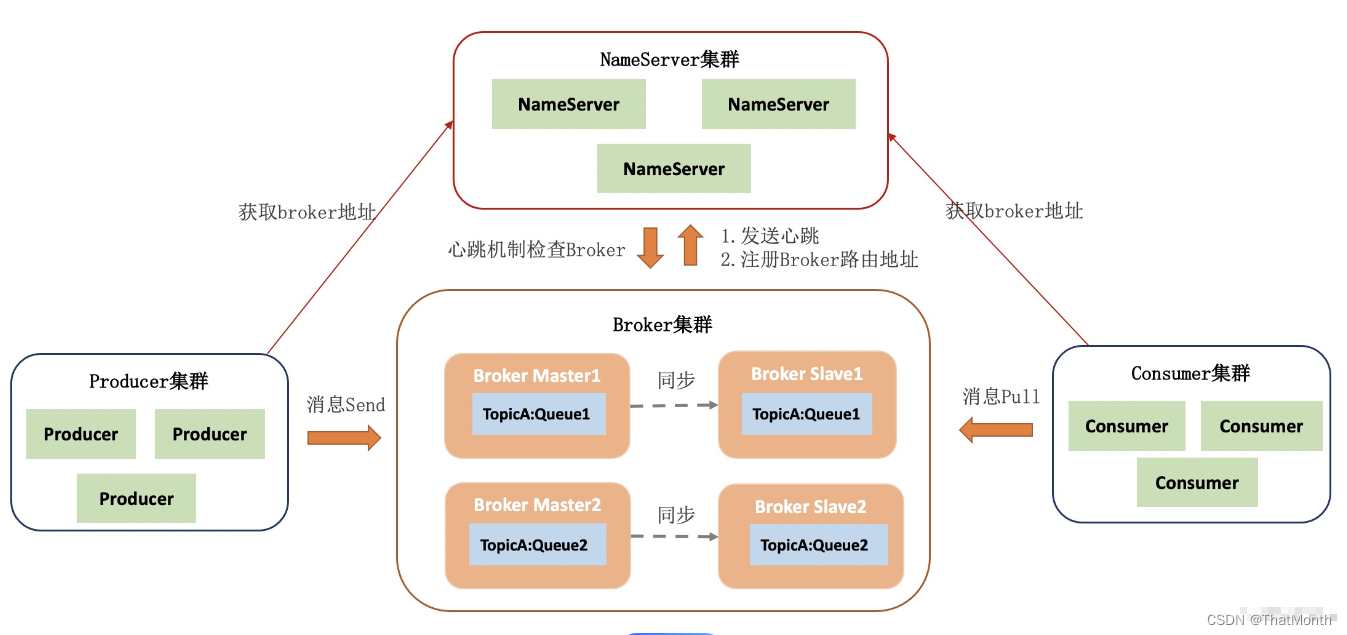
RocketMQ教程(三):RocketMQ的核心组件
四个核心组件 RocketMQ 的架构采用了典型的分布式系统设计理念,以确保高性能、高可用和可扩展性。RocketMQ 主要由四个核心组件构成:NameServer、Broker、Producer 和 Consumer。下面是对这些组件以及它们在 RocketMQ 中的角色和功能的概述: 1. NameServer 角色和功能:Name…...

46.SQLserver中按照多条件分组:查询每个地方的各种水果的种植数量,新增时,一个地方同时有几种水果,只插入一条记录,同时多种水果之间使用|隔开
1.SQLserver中按照多条件分组 ,分组条件包括(一个字段使用|进行分割,如:apple|orange,查询时,apple和orange分别对应一条数据) 例如:SQL如下: SELECT FROM ( SELECT CDFBM 地方编码…...
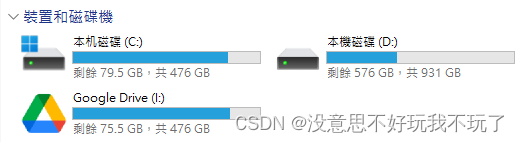
C盘满了怎么办,Windows11的C盘没有磁盘清理选项怎么办,一次搞定
问题: 太久没清电脑了,满的跟垃圾堆一样。。。C盘红色看上去很不妙。 一. C盘满了怎么办: 1. 删除临时文件 找到 C:\Windows\Temp,进入Temp资料夹,选中所有文件夹和文件,按下ShiftDelete键,彻…...

「动态规划」当小偷改行去当按摩师,会发生什么?
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
