重构大学数学基础_week04_从点积理解傅里叶变换
这周我们来看一下傅里叶变换。傅里叶变换是一种在数学和许多科学领域中广泛应用的分析方法,它允许我们将信号或函数从其原始域(通常是时间域或空间域)转换到频域表示。在频域中,信号被表示为其组成频率的幅度和相位,这为理解和操作信号提供了一种强大的方式。
这次我不会从它普遍的推导方式来理解,而是从一个更简单的角度来理解----向量的点积。
向量点积
先简单介绍一下向量的点积。假如我们现在有一个向量a长度为6,又有一个向量b长度为8,它们的夹角为60°,那么它们的点积的就是用它们的模长乘以夹角的余弦值,得到24.

那么这样定义有什么用呢?它得出来的数值说明了什么呢?我们现在把夹角调小到30°,现在我们就看到啊,向量b在a方向上得投影变得比之前长了,而点积的结果也变成了24倍的根号3。

大家观察一下啊,角度调整前后的向量b谁和向量a更像啊?那自然是夹角更小的那个了,所以点积或者说点乘这样子来定义的一大作用呢,就是可以衡量一个东西和另一个东西有多像,也就是相似度,
而点积出来的数值越大,相似度呢就越高。这时如果把向量具象化为一个观察者,而观察者呢只能看到和感知到它自己这个维度方向上的东西,所以向量b在向量a 的眼里呢也还是一个向量,并且和自己是一条线上的。

那么在a的眼里,b向量有多长呢?那就得算向量b在a方向上的投影是多少了,也就是拿b向量的模长乘以他们夹角的余弦。
![]()
如果用上刚刚点乘的定义呢,就是ab点积再除以a的模长,
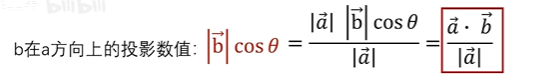
这个就是b在a上的投影长度了。如果向量b垂直于向量a,那么b在a上的投影就是0,点积结果就是0。也就是说它们两个一点都不“像”,那么我们a作为观察者,它压根就感知不到向量b的存在。
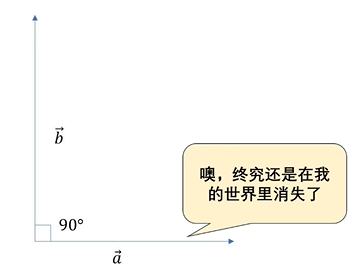
当夹角变成钝角的时候,情况又出现了新的变化,向量b在向量a的方向上又有了投影,只不过方向和刚刚相反了,点积就变成了负值,它们仍然具有相似性。
既然引出了观察者这个概念,那么我们就可以从一个全新的角度去看了,虽然每一个观察者都只能看到一个片面,但是我们把所有观察者都看到的都综合起来,就可以得到真相了。
观察者角度看向量分解
我们找来两个相互垂直的观察者i和j,它们的长度都是1,你想看i眼里的向量m,那么我们就可以用i和m进行点积,假如我们得到的数值是4,同理,看j眼里的向量m可以用j和m进行点积,结果为3,这时候向量m就可以表示为4i加3j了。

可以看出,向量m对观察者向量i的影响更大,它们也更相似。大家注意,上面两个观察者i和j的长度被定义为1,这其实就是归一化操作,为什么要归一化呢?那总不能让作为基准的东西高矮胖瘦什么都有吧?而且归一化可以保证各个观察者在能量上是一致的,方便后续数据的处理,如果不进行归一化,那么后续处理数据又得一个一个来区别对待,那就相当麻烦。
如果向量长度不为一怎么办?那么我们把它归为1.现在有一个向量a,我们直接除以它的模长,就可以得到归一化后的观察者了,其实就是a方向的单位向量了。

那刚刚的4i+3j,I和j都是单位向量,而4和3是投影系数,也就是在不同方向观察者看到的量是多少。

好我们再回到刚刚那个例子,在a 眼里向量b可以这么表达:a点乘b再除以a的模长,就是b在a方向的投影,然后再乘以a的归一化向量,也就是a 除以自己的模长。
 我们可以看出来,如果观察者不归一,那么你的系数就要归一。
我们可以看出来,如果观察者不归一,那么你的系数就要归一。
一句话小结一下,观察者理论就是对于给定的目标,让若干个归一化的每个观察者都记录一个数据,而这些数据就是我们想要的东西了,所以点积就是观察者了解一个未知事物的手段。
连续函数的点积
我们放到直角坐标系当中去看。我们都知道在直角坐标系下两个向量X[x1,x2,x3,x4]和Y[y1,y2,y3,y4]的点积是对应的分量相乘再相加,推广到n维也是如此。现在我们来思考这样一种事情,假如我们有两个向量Xn[x1,x2,x3,x4,…xn] 和Yn[y1,y2,y3,…yn] 我们把Xn的每一个分量均匀放在时间轴t上,假设范围是(t1,t2),那么我们就可以看出来,这是一个t1到t2的离散函数,x1x2x3等等是函数值。

当n 越来越大趋于无穷的时候,那么均匀分布在t轴上的数就会越来越多,直到连续。那么这就是一个连续函数X(t),t∈[t1,t2],Yn同理。
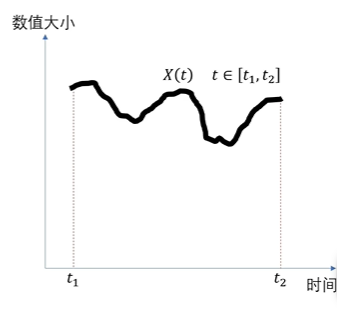
这样我们就可以看出来,一个连续的函数等价于无穷维的向量。那么结合向量的点积
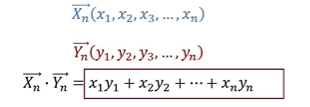 ,这些就是对应点的函数值相乘,当它们是连续函数的时候,直接用两个函数相乘就行了,就是X(t)乘以Y(t).
,这些就是对应点的函数值相乘,当它们是连续函数的时候,直接用两个函数相乘就行了,就是X(t)乘以Y(t).
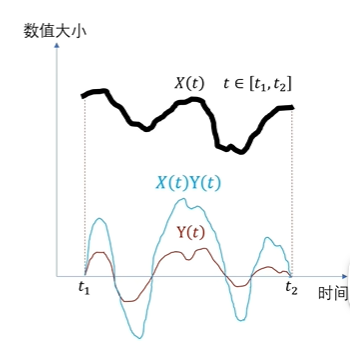
那么相加的动作,在连续函数当中就是求积分,如果定义域是t1,t2的闭区间,那么式子就是这样子
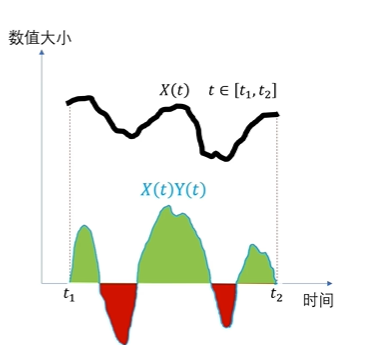
从图像上来看,这个式子的数值是大于0的,也就是说,它们之间是存在一些相似度的。那么上面的呢就是连续函数点乘的定义了。
从点积推导傅里叶变换
好,那么现在让我们把目光放在傅里叶级数上来,傅里叶级数是由一系列简单的正余弦函数作为基,例如2pi周期的函数的基就是cost,cos2t,cos3t等等,这些基是通过不同频率来进行区分的,它们可以看到目标函数在自己频率世界中的投影,也就是影响是多少。当然也可以说是看目标函数和观察者自己本身的相似度有多少。
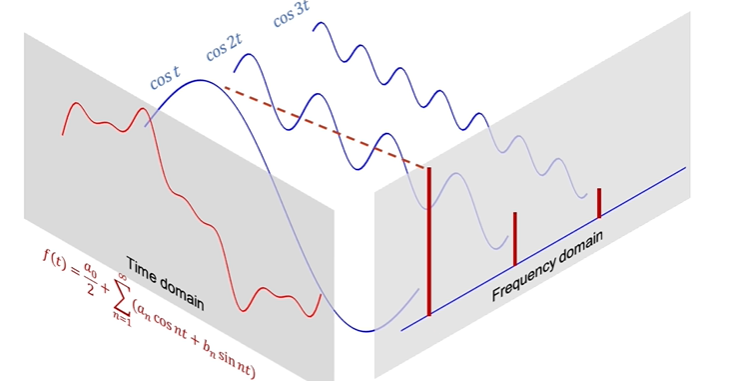
如果高频的观察者和目标函数相似度更高,那么就说明原函数的高频成分就更多。例如,我们有一个目标函数f(t),我们想看cosnt和目标函数相似度有多少,即成分的高低,那么我们直接让二者点乘即可,即从[-pi,pi],
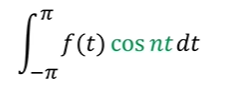
如果你还想进一步看一下f(t)在cosnt上具体的投影是多少呢,那就离不开归一化操作了,刚才已经讲过了要么观察者是归一的要么系数是归一的。连续函数不就是连续无穷维向量吗?所以连续函数的模长就是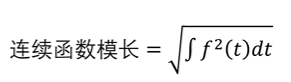 。那么cosnt的模长就是
。那么cosnt的模长就是 ,其实连续函数的模长有一个专有名词叫做2-范数。很明显cosnt这个观察者没有归一,所以投影系数呢就得归一,我们看之前总结的公式。代入后就是
,其实连续函数的模长有一个专有名词叫做2-范数。很明显cosnt这个观察者没有归一,所以投影系数呢就得归一,我们看之前总结的公式。代入后就是

这个式子是不是非常眼熟?它就是傅里叶级数求An的公式,对应到不同频率基的振幅。这样我们就可以求出原函数在不同频率下的投影是多少了。
好,我们接下来更进一步进入到傅里叶级数的复变换形式。上周我们都了解了欧拉公式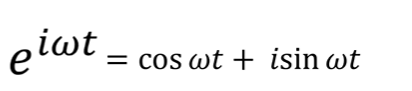 ,那么我们就可以把
,那么我们就可以把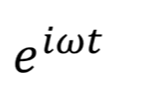 代入进去了。
代入进去了。
不过要注意一件事情,两个复函数的点乘是取后者的共轭函数进行计算的。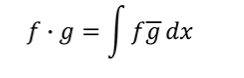
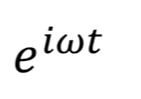 取代了之前的cosnt成为了新的观察者,那么让它来对f(t)进行点乘来看相似度有多少,
取代了之前的cosnt成为了新的观察者,那么让它来对f(t)进行点乘来看相似度有多少,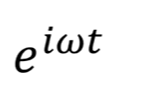 的共轭复数是
的共轭复数是![]() ,进行点乘之后有
,进行点乘之后有
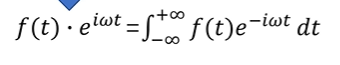 ,而且我们可以看到,观察者已经归一了,因为它表示的都是半径为1的旋转,那么现在我们再看看这个公式,这其实就是连续函数的傅里叶变换的公式。我们积分出来的结果一般都是一个关于角频率w的复函数,那么这个复函数的模就可以理解为我们前面所说过的投影数。
,而且我们可以看到,观察者已经归一了,因为它表示的都是半径为1的旋转,那么现在我们再看看这个公式,这其实就是连续函数的傅里叶变换的公式。我们积分出来的结果一般都是一个关于角频率w的复函数,那么这个复函数的模就可以理解为我们前面所说过的投影数。
以上就是从点积或者说点乘角度来理解傅里叶变换,希望能帮助到大家对傅里叶变换有更深层次的认识。
总结
1.点积就是计算A与B之间的相似程度。
2.一个n维向量存在n个基,第i个基与其进行点积,可以得到该向量在第i个基上的相似度。
3.无穷维的向量可以看作是一个连续的函数,此时点积可看作积分。
4.引入欧拉公式,将目标函数与不同基点乘,从而得到不同频率的成分大小,这就是连续傅里叶变换。
应用
- 图像压缩与增强:傅里叶变换可以将图像转换到频域,从而分离出代表图像细节的高频分量和表示图像结构的低频分量。这一特性被用于图像压缩,通过去除或减少高频噪声来减小图像大小,同时保持视觉质量。在图像增强方面,可以通过调整频域系数来改善图像的清晰度或进行去模糊处理。
- 音频信号处理:在语音识别、音乐分类和音频降噪等任务中,傅里叶变换用于分析音频信号的频率组成,帮助识别特定的声音特征,从而提高处理的准确性和效率。
- 时序数据分析:在处理时间序列数据(如股票价格、传感器读数)时,傅里叶变换能够揭示数据中的周期性成分,帮助预测未来趋势、异常检测和模式识别。
- 降维和特征工程:在高维数据集中,傅里叶变换可以揭示数据的频率特性,通过选择或构造基于频率的特征,降低数据维度,提高机器学习模型的训练效率和泛化能力。
相关文章:
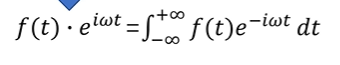
重构大学数学基础_week04_从点积理解傅里叶变换
这周我们来看一下傅里叶变换。傅里叶变换是一种在数学和许多科学领域中广泛应用的分析方法,它允许我们将信号或函数从其原始域(通常是时间域或空间域)转换到频域表示。在频域中,信号被表示为其组成频率的幅度和相位,这…...

Shell以及Shell编程
Shell的任务 ①分析命令; ②处理通配符、变量替换、命令替换、重定向、管道和作业控制; ③搜索命令并执行。 内部命令:内嵌在Shell中。 外部命令:存在于磁盘上的独立可执行文件。 #!/bin/bash #! 称为一个幻数&…...

从记忆到想象:探索AI的智能未来
引言 人工智能(AI)在信息处理、数据分析和任务自动化等方面展现了强大的能力。然而,在人类独有的记忆和想象力领域,AI仍然有很长的路要走。加利福尼亚大学戴维斯分校的心理学和神经科学教授查兰兰加纳特(Charan Ranga…...
“安全生产月”专题报道:AI智能监控技术如何助力安全生产
今年6月是第23个全国“安全生产月”,6月16日为全国“安全宣传咨询日”。今年全国“安全生产月”活动主题为“人人讲安全、个个会应急——畅通生命通道”。近日,国务院安委会办公室、应急管理部对开展好2024年全国“安全生产月”活动作出安排部署。 随着科…...
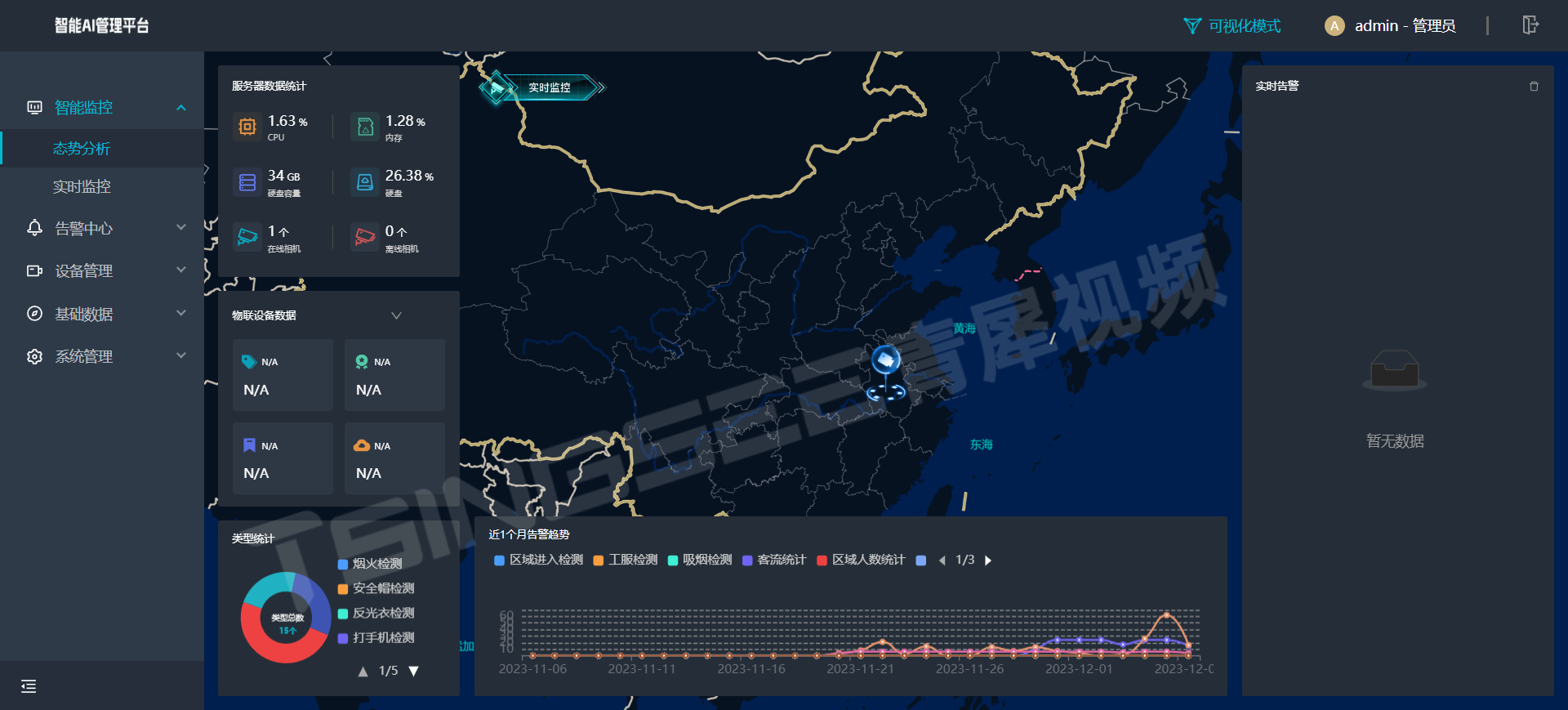
【转】ES, 广告索引
思考: 1)直接把别名切换到上一个版本索引 --解决问题 2)广告层级索引如何解决? -routing、join 3)查询的过程:query and fetch, 优化掉fetch 4)segment合并策略 5)全量写入时副…...

Unity学习要点
前言 学习Unity作为游戏开发的强大工具,对于初学者来说,掌握一些基础而实用的技巧是非常重要的。这不仅能帮助你更快地上手,还能在项目开发过程中提高效率。以下是一些Unity初学者的使用技巧,希望能为你的学习之旅提供帮助。 ##…...

简单使用phpqrcode 生成二维码图片
$path ROOT_PATH; //tp项目根路径 require_once $path.vendor/phpqrcode/phpqrcode.php; //加载phpqrcode库 $url http://.$_SERVER[HTTP_HOST]./home/index/detail?id.$param[id]; $value $url; //二维码内容 $errorCorrectionLevel L; //容错级别 $mat…...
软考架构-计算机网络考点
会超纲,3-5分 网络分类 按分布范围划分 局域网 LAN 10m-1000m左右 房间、楼宇、校园 传输速率高 城域网 MAN 10km 城市 广域网 WAN 100km以上 国家或全球(英特网) 按拓扑结构划分 总线型:利用率低、干…...
)
渗透测试之内核安全系列课程:Rootkit技术初探(三)
今天,我们来讲一下内核安全! 本文章仅提供学习,切勿将其用于不法手段! 目前,在渗透测试领域,主要分为了两个发展方向,分别为Web攻防领域和PWN(二进制安全)攻防领域。在…...

大模型日报2024-06-08
大模型日报 2024-06-08 大模型资讯 AI研究:通过消除矩阵乘法实现高效的大语言模型 摘要: 该AI研究探讨了通过消除矩阵乘法来实现高效且可扩展的大语言模型(LLMs)。此方法旨在提升模型性能,提供更快速和高效的计算方案。 AWS大力投…...

leetcode 1631.最小体力消耗路径
思路:BFS二分 这道题和洛谷上的那个“汽车拉力赛”那道题很相似,但是这道题相较于洛谷那个来说会简单一些。 这里作者一开始写的时候思路堵在了怎么在BFS中用二分,先入为主的以为需要先写出来搜索函数然后再去处理二分的事,但是…...

【ARM64 常见汇编指令学习 19.2 -- ARM64 地址加载指令 ADR 详细介绍】
文章目录 地址加载指令 ADRADR 指令使用场景例子注意事项 地址加载指令 ADR ARMv8 架构引入了一系列的改进和扩展,包括对汇编指令集的更新。在这之中,ADR 指令是一个重要的组成部分,它用于计算并加载一个地址到寄存器。 ADR 指令 ADR 指令…...

vscode输出控制台中文显示乱码最有效解决办法
当VSCode的输出控制台中文显示乱码时,一个有效的解决办法是通过设置环境变量来确保编码的正确性。以下是解决方式: 首先,设置环境变量以修正乱码问题: 如果上述方法没有解决乱码问题,请继续以下步骤: 右键…...
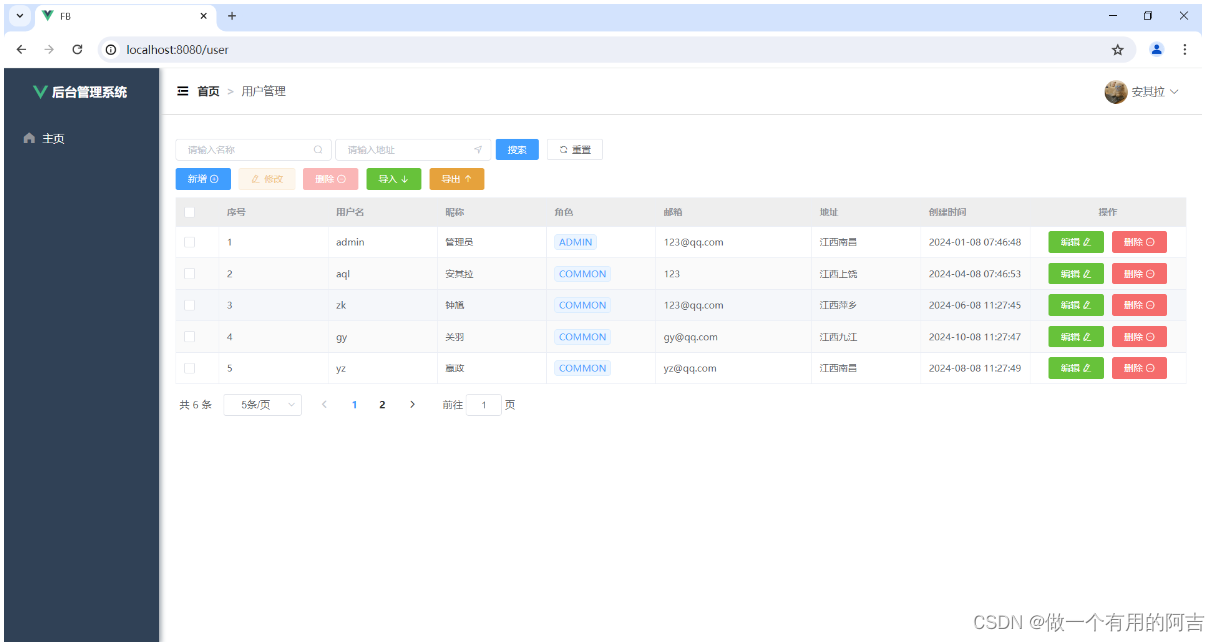
springboot + Vue前后端项目(第十五记)
项目实战第十五记 写在前面1.后端接口实现1.1 用户表添加角色字段1.2 角色表增加唯一标识字段1.3 UserDTO1.4 UserServiceImpl1.5 MenuServiceImpl 2. 前端实现2.1 User.vue2.2 动态菜单设计2.2.1 Login.vue2.2.2 Aside.vue 2.3 动态路由设计2.3.1 菜单表新增字段page_path2.3.…...

如何在Windows 11中恢复丢失的快速访问菜单?这里提供解决办法
序言 在电脑的“快速访问”菜单中找不到固定的项目?或者,整个菜单对你来说已经消失了吗?无论哪种方式,你都可以强制你的电脑恢复菜单并显示其中的所有项目。以下是如何在你的Windows 11电脑上做到这一点。 将文件资源管理器设置为打开到主页 当你在文件资源管理器的左侧…...

变声器软件免费版有哪些?国内外12大热门变声器大盘点!(新)
变声软件是一种人工智能AI音频处理工具,允许用户实时修改自己的声音或改变预先录制的音频。这些软件解决方案可提供不同的效果,如改变声音的音调或速度,或将我们的声音转换成其他人或其他东西的声音,如名人、卡通人物、机器人或不…...
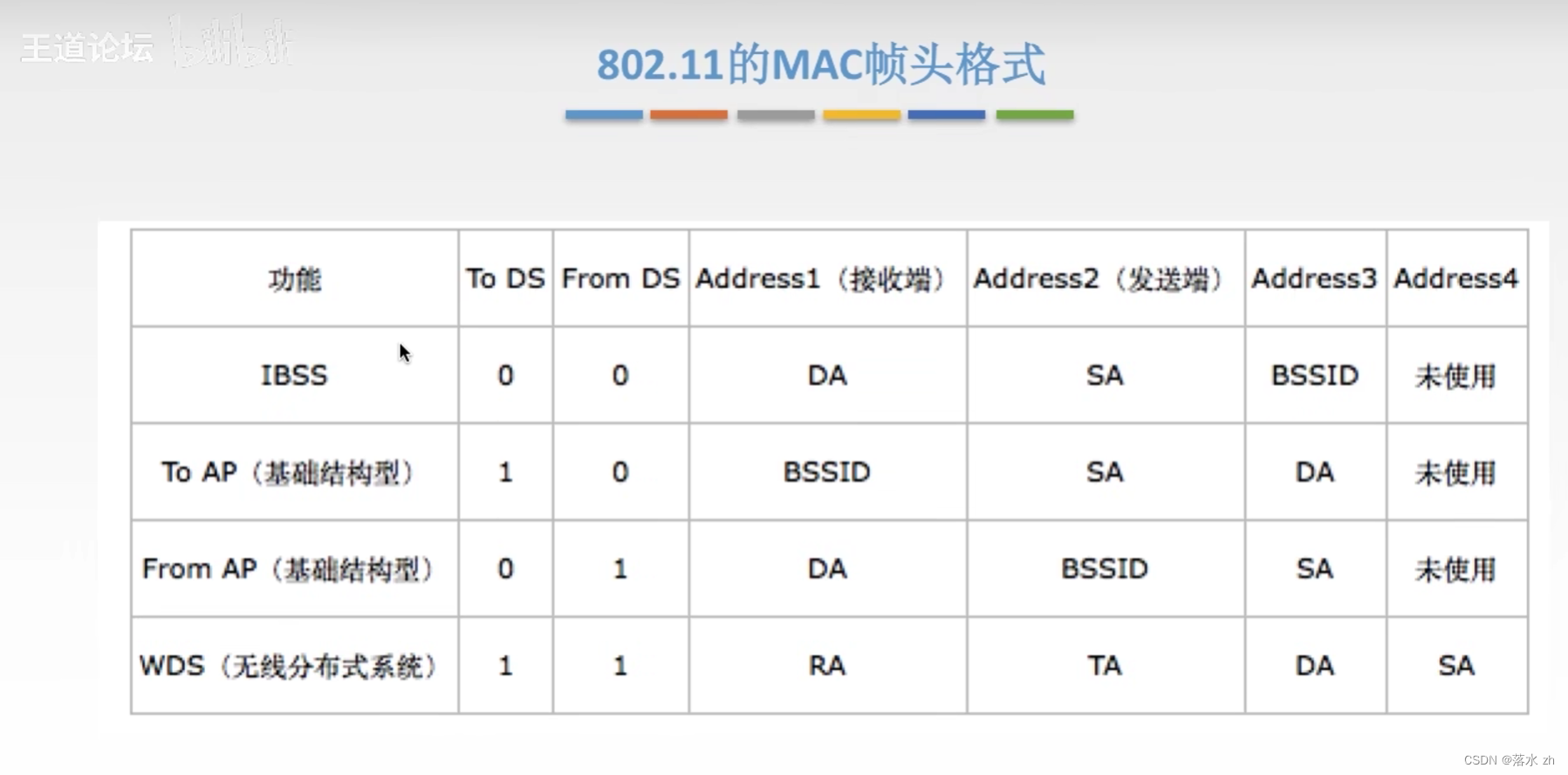
计算机网络 —— 数据链路层(无线局域网)
计算机网络 —— 数据链路层(无线局域网) 什么是无线局域网IEEE 802.11主要标准及其特点: 802.11的MAC帧样式 我们来看看无线局域网: 什么是无线局域网 无线局域网(Wireless Local Area Network,简称WLAN…...

SpringBoot图书管理系统【附:资料➕文档】
前言:我是源码分享交流Coding,专注JavaVue领域,专业提供程序设计开发、源码分享、 技术指导讲解、各类项目免费分享,定制和毕业设计服务! 免费获取方式--->>文章末尾处! 项目介绍048: 图…...

shell简介
一、Shell 概念定义 Shell 是用 C 语言编写的程序,是用户使用 Linux 的桥梁,既是命令语言又是程序设计语言。 shell 脚本为 Shell 编写的脚本程序,常说的 shell 通常指 shell 脚本。 包含一系列命令的文本文件,这些命令按照特定…...
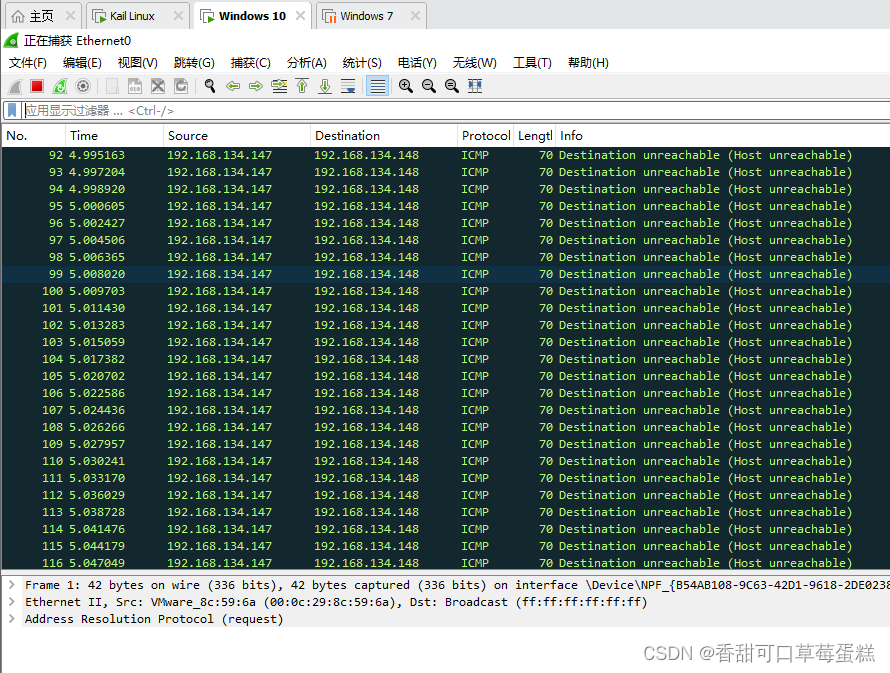
使用 Scapy 库编写 ICMP 不可达攻击脚本
一、介绍 ICMP不可达攻击是一种利用ICMP(Internet Control Message Protocol)不可达消息来干扰或中断目标系统的网络通信的攻击类型。通过发送伪造的ICMP不可达消息,攻击者可以诱使目标系统认为某些网络路径或主机不可达,从而导致…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
