git 空仓库笔记
标识身份,建议先完成 Git 全局设置
git config --global user.name “账号”
git config --global user.email “email”
方式一:克隆仓库
git clone https://url/your.git
cd your_path
touch README.md
git add README.md
git commit -m "add README"
git push -u origin master方式二:已有文件夹或仓库
cd existing_folder
git init
git remote add origin https://url/your.git
git add .
git commit
git push -u origin master
方式三:导入代码库
git clone --bare https://url/your.git
cd your_path
git remote set-url origin https://url/your.git
git push origin --tags && git push origin --all
相关文章:

git 空仓库笔记
标识身份,建议先完成 Git 全局设置 git config --global user.name “账号” git config --global user.email “email” 方式一:克隆仓库 git clone https://url/your.git cd your_path touch README.md git add README.md git commit -m "add …...
)
字母异位词分组(charyw)
字母异位词分组 题目描述 给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串。 输入格式 第一行正整数n,表示有n个字符串(1<n<1000) 第二行n个字符串,空格隔开 输出格式 多组字母…...

力扣 41.缺少的第一个正整数
题目描述: 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 示例 1: 输入:nums [1,2,0] 输出:3 解释:范围 …...
Git从入门到放弃
由于我的Git学的不太好,所以为了能够将以后我的学习笔记能够整理的更好,我先要系统的学习一下git,文章由此产生。 文章笔记源自尚硅谷Git入门到精通全套教程视频内容 1 进入官网 学习新技术的第一步需要熟悉官网,Git也不例外。ht…...

003.数据分析_PandasSeries对象
我 的 个 人 主 页:👉👉 失心疯的个人主页 👈👈 入 门 教 程 推 荐 :👉👉 Python零基础入门教程合集 👈👈 虚 拟 环 境 搭 建 :👉&…...

【介绍下什么是Kubernetes编排系统】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...

linux防止nmap扫描
1、首先关闭Centos7自带的firewalld [rootnode ~]# systemctl disable firewalld.service && systemctl stop firewalld.service 2、安装iptables服务 [rootnode ~]# yum install iptables-services iptables-devel -y [rootnode ~]# systemctl enable iptables …...

基于SpringBoot的装饰工程管理系统源码数据库
如今社会上各行各业,都喜欢用自己行业的专属软件工作,互联网发展到这个时候,人们已经发现离不开了互联网。新技术的产生,往往能解决一些老技术的弊端问题。因为传统装饰工程项目信息管理难度大,容错率低,管…...

2024前端面试准备2-JS基础知识回顾
变量类型和计算 1.值类型和引用类型的区别 常见值类型:undefined(定义undefined只能用let,不能用const)、字符串、bool、number、 Symbol; 常见引用类型: 对象, 数组、null(特殊引用类型,指针指向为空地址) 、function(特殊引用类型); 值类型的值直接存储在栈中;引用类型值存储…...
)
C++ 环形链表(解决约瑟夫问题)
约瑟夫问题描述: 编号为 1 到 n 的 n 个人围成一圈。从编号为 1 的人开始报数,报到 m 的人离开。下一个人继续从 1 开始报数。n-1 轮结束以后,只剩下一个人,问最后留下的这个人编号是多少? 约瑟夫问题例子:…...
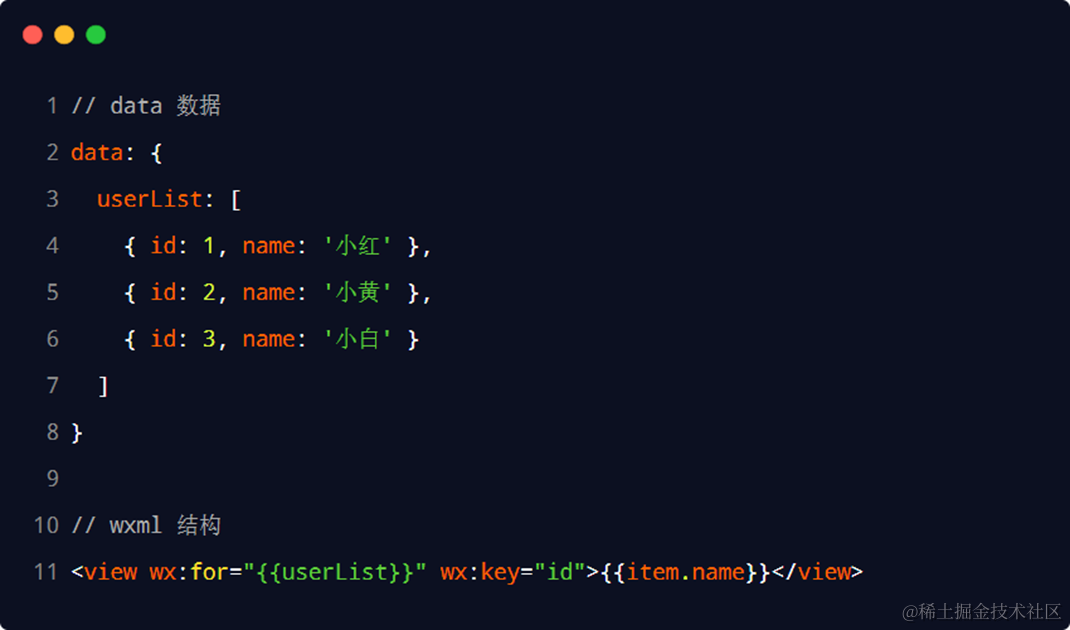
【微信小程序】模板语法
数据绑定 对应页面的 js 文件中 定义数据到 data 中: 在页面中使用 {{}} 语法直接使用: 事件绑定 事件触发 常用事件: 事件对象的属性列表(事件回调触发,会收到一个事件对象 event,它的详细属性如下&…...

深入了解 C 语言 Bug
目录 一、引言二、Bug的定义三、Bug的由来四、Bug的影响五、应对 Bug 的方法六、结论 一、引言 1、在 C 语言的编程世界中,Bug 是一个我们无法回避的话题。 2、Bug,简单来说,就是程序中存在的错误或缺陷。它可以表现为程序运行结果的异常、崩…...

Redis 内存回收
文章目录 1. 过期key处理1.1 惰性删除1.2 周期删除 2. 内存淘汰策略 Redis 中数据过期策略采用定期删除惰性删除策略结合起来,以及采用淘汰策略来兜底。 定期删除策略:Redis 启用一个定时器定时监视所有的 key,判断key是否过期,过…...

【讲解下ECMAScript和JavaScript之间有何区别?】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...

Linux基本指令查询硬件信息001
在Linux系统中查询硬件信息可以通过多种命令行工具完成,本章主要讲述如何查询Linux硬件信息。 操作系统: CentOS Stream 9 操作步骤: 指令uname -a : 显示内核版本、硬件名称、操作系统等基本信息。 [rootlocalhost ~]# uname -a Linux …...
:集成Guava 库实现布隆过滤器(Bloom Filter))
Spring Boot(七十四):集成Guava 库实现布隆过滤器(Bloom Filter)
之前在redis(17):什么是布隆过滤器?如何实现布隆过滤器?中介绍了布隆过滤器,以及原理,布隆过滤器有很多实现和优化,由 Google 开发著名的 Guava 库就提供了布隆过滤器(Bloom Filter)的实现。在基于 Maven 的 Java 项目中要使用 Guava 提供的布隆过滤器,只需要引入以…...
二叉查找树详解
目录 二叉查找树的定义 二叉查找树的基本操作 查找 插入 建立 删除 二叉树查找树的性质 二叉查找树的定义 二叉查找树是一种特殊的二叉树,又称为排序二叉树、二叉搜索树、二叉排序树。 二叉树的递归定义如下: (1)要么二…...
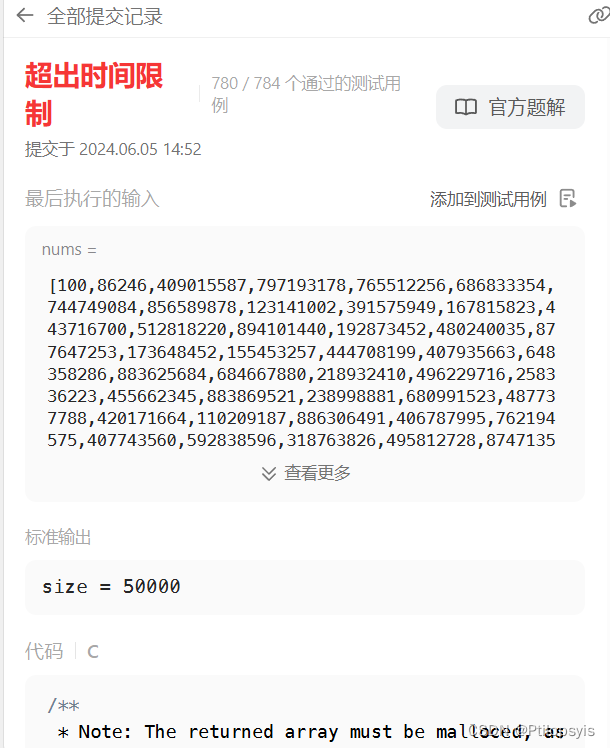
3072. 将元素分配到两个数组中 II
题目 给你一个下标从 1 开始、长度为 n 的整数数组 nums 。 现定义函数 greaterCount ,使得 greaterCount(arr, val) 返回数组 arr 中 严格大于 val 的元素数量。 你需要使用 n 次操作,将 nums 的所有元素分配到两个数组 arr1 和 arr2 中。在第一次操…...

城市之旅:使用 LLM 和 Elasticsearch 简化地理空间搜索(二)
我们在之前的文章 “城市之旅:使用 LLM 和 Elasticsearch 简化地理空间搜索(一)”,在今天的练习中,我将使用本地部署来做那里面的 Jupyter notebook。 安装 Elasticsearch 及 Kibana 如果你还没有安装好自己的 Elasti…...

【知识点】 C++ 构造函数 参数类型为右值引用的模板函数
C 构造函数是一种特殊的成员函数,用于初始化类对象。C 中的构造函数主要分为以下几种类型: 默认构造函数(Default Constructor)参数化构造函数(Parameterized Constructor)拷贝构造函数(Copy C…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
