二叉查找树详解
目录
二叉查找树的定义
二叉查找树的基本操作
查找
插入
建立
删除
二叉树查找树的性质
二叉查找树的定义
二叉查找树是一种特殊的二叉树,又称为排序二叉树、二叉搜索树、二叉排序树。
二叉树的递归定义如下:
(1)要么二叉查找树是一棵空树。
(2)要么二叉查找树由根节点、左子树、右子树组成,其中左子树和右子树都是二叉查找树,且左子树上所以结点的数据域均小于或等于根节点的数据域,右子树上的所有结点的数据域均大于根节点的数据域。
二叉查找树的基本操作
查找
进行二叉树的查找操作时,由于无法确定二叉树的具体特性,因此只能对左右子树都进行递归遍历。但是二叉查找树的性质决定了可以只选择一棵子树进行遍历。因此查找将会是从根节点查找的一条路径,故最坏时间复杂度是,其中h是二叉查找树的高度。于是就可以得到查找操作的基本思路:
(1)如果当前根节点root为空,说明查找失败,返回。
(2)如果需要查找的x等于当前根节点的数据域root->data,查找成功,访问。
(3)如果需要查找的x小于当前根节点的数据域root->data,说明应该往左子树查找,因此向root->lchild递归。
(4)如果需要查找的x大于当前结点的数据域root->data,则应该往右子树查找,因此向root->rchild递归。
void search(node* root,int x){if(root==NULL){printf("search failed\n");return;}if(x==root->data){printf("%d\n",root->data);}else if(x<root->data){search(root->lchild,x);}else{search(root->rchild,x);}
}可以看到,和普通二叉树的查找函数不同,二叉查找树的查找在于对左右子树的选择递归。在普通二叉树中,无法确定需要查找的值x到底是在左子树还是右子树,但是在二叉查找树中就可以确定,因为二叉查找树中的数据域顺序总是左子树<根节点<右子树。
插入
对一棵二叉查找树来说,查找某个数据域的结点一定是沿着确定的路径进行的。因此,当对某个需要查找的值在二叉查找树中查找成功,说明结点已经存在。反之,如果这个需要查找的值在二叉查找树中查找失败,那么说明查找失败的地方一定是结点需要插入的地方。因此可以在上面查找操作的基础上,在root==NULL时新建需要插入的点。
void insert(node* &root,int x){if(root==NULL){root=newNode[x];return;}if(x==root->data){return;}else if(x<root->data){insert(root->lchild,x);}else{insert(root->rchild,x);}
}建立
node* Create(int data[],int n){node* root=NULL;for(int i=0;i<n;i++){insert(root,data[i]);}return root;
}需要注意的是,即使是一组相同的数字,如果插入它们的顺序不同,最后生成的二叉查找树也可能不同。
删除
把二叉查找树中比结点权值小的最大结点称为该结点的前驱,而把比结点权值大的最小结点称为该结点的后继。显然,结点的前驱是该结点左子树的最右结点(也就是从左子树根节点开始不断沿着rchild往下直到rchild为NULL时的结点),而结点的后继则是该结点右子树的最左节点(也就是从右子树根节点开始不断沿着lchild往下直到lchild为NULL时的结点)。下面两个函数用来寻找以root为根的树中最大或最小权值的结点,用以辅助寻找结点的前驱和后继:
//寻找以root为根结点的树中的最大权值结点
node* findMax(node* root){while(root->rchild!=NULL){root=root->rchild;}return root;
}
//寻找以root为根结点的树中的最小权值结点
node* findMin(node* root){while(root->lchild!=NULL){root=root->lchild;}return root;
} 删除操作的基本思路如下:
(1)如果当前结点root为空,说明不存在权值为给定权值x的结点,直接返回。
(2)如果当前结点root的权值恰为给定的权值x,说明找到了想要删除的结点,此时进入删除处理。如果当前结点root不存在左右孩子,说明是叶子节点,直接删除。如果当前结点root存在左孩子,那么在左子树中寻找结点前驱pre,然后让前驱的数据覆盖root,接着在左子树中删除结点pre。如果当前结点root存在右孩子,那么在右子树中寻找结点后继next,然后让next的数据覆盖root,接着在右子树中删除结点next。
(3)如果当前结点root的权值大于给定权值的x,则在左子树中递归删除权值为x的结点。
(4)如果当前结点root的权值小于给定权值的x,则在右子树中递归删除权值为x的结点。
//寻找以root为根结点的树中的最大权值结点
node* findMax(node* root){while(root->rchild!=NULL){root=root->rchild;}return root;
}
//寻找以root为根结点的树中的最小权值结点
node* findMin(node* root){while(root->lchild!=NULL){root=root->lchild;}return root;
}
void deleteNode(node* &root,int x){if(root==NULL){return;}if(root->data==x){if(root->lchild==NULL&&root->rchild==NULL){root==NULL;}else if(root->lchild!=NULL){node* pre=findMax(root->lchild);root->data=pre->data;deleteNode(root->lchild,pre->data);}else{node* next=findMin(root->rchild);root->data=next->data;deleteNode(root->rchild,next->data);}}else if(root->data>x){deleteNode(root->lchild,x);}else{deleteNode(root->rchild,x);}
}但是也要注意,总是优先删除前驱或后继容易导致树的左右子树高度极度不平衡,使得二叉查找树退化成一条链。解决这一问题的办法有两种:一种是每次交替删除前驱或后继;另一种是记录子树高度,总是优先在高度较高的一棵子树里删除结点。
二叉树查找树的性质
二叉查找树一个实用的性质:对二叉查找树进行中序遍历,遍历的结果是有序的。
另外,如果合理调整二叉查找树的形态,使得树上的每个结点都尽量有两个子节点,这样整个二叉查找树的高度就会很低,也即树的高度大概在的级别。
例题
给出N个正整数来作为一棵二叉排序树的结点插入顺序,问:这串序列是否是该二叉排序树的先序序列或是该二叉排序树的镜像树的先序序列。所谓镜像树是指交换二叉树的所有结点的左右子树而形成的树(也即左子树所有结点数据域大于或等于根节点,而根节点数据域小于右子树所有结点的数据域)。如果是,则输出YES,并输出对应的树的后序序列;否则,输出NO。
思路
通过给定的插入序列,构建出二叉排序树。对镜像树的先序遍历只需要在原树的先序遍历时交换左右子树的访问顺序即可。
//镜像树先序遍历,结果存放于vi
void preordermirror(node* root,vector<int>&vi){if(root==NULL){return;}vi.push_back(root->data);preordermirror(root->right,vi);preordermirror(root->left,vi);
} 注意点
使用vector来存放初始序列、先序序列、镜像树先序序列,可以方便相互之间的比较。若使用数组,则比较操作需要使用循环才能实现。
#include<cstdio>
#include<vector>
using namespace std;
struct node{int data;node* left,*right;
};
vector<int> origin,pre,preM,post,postM;
void insert(node* &root,int data){if(root==NULL){root=new node;root->data=data;root->left=root->right=NULL;return;}if(data<root->data){insert(root->left,data);}else{insert(root->right,data);}
}
void preorder(node* root,vector<int> &vi){if(root==NULL){return;}vi.push_back(root->data);preorder(root->left,vi);preorder(root->right,vi);
}
void preordermirror(node* root,vector<int> &vi){if(root==NULL){return;}vi.push_back(root->data);preordermirror(root->right,vi);preordermirror(root->left,vi);
}
void postorder(node* root,vector<int> &vi){if(root==NULL){return;}postorder(root->left,vi);postorder(root->right,vi);vi.push_back(root->data);
}
void postordermirror(node* root,vector<int> &vi){if(root==NULL){return;}postordermirror(root->right,vi);postordermirror(root->left,vi);vi.push_back(root->data);
}
int main(){int n,data;node* root=NULL;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&data);origin.push_back(data);insert(root,data);}preorder(root,pre);preordermirror(root,preM);postorder(root,post);postordermirror(root,postM);if(origin==pre){printf("YES\n");for(int i=0;i<post.size();i++){printf("%d",post[i]);if(i<post.size()-1){printf(" ");}}}else if(origin==preM){printf("YES\n");for(int i=0;i<postM.size();i++){printf("%d",postM[i]);if(i<postM.size()-1){printf(" ");}}}else{printf("NO\n");return 0;}
}相关文章:
二叉查找树详解
目录 二叉查找树的定义 二叉查找树的基本操作 查找 插入 建立 删除 二叉树查找树的性质 二叉查找树的定义 二叉查找树是一种特殊的二叉树,又称为排序二叉树、二叉搜索树、二叉排序树。 二叉树的递归定义如下: (1)要么二…...
3072. 将元素分配到两个数组中 II
题目 给你一个下标从 1 开始、长度为 n 的整数数组 nums 。 现定义函数 greaterCount ,使得 greaterCount(arr, val) 返回数组 arr 中 严格大于 val 的元素数量。 你需要使用 n 次操作,将 nums 的所有元素分配到两个数组 arr1 和 arr2 中。在第一次操…...

城市之旅:使用 LLM 和 Elasticsearch 简化地理空间搜索(二)
我们在之前的文章 “城市之旅:使用 LLM 和 Elasticsearch 简化地理空间搜索(一)”,在今天的练习中,我将使用本地部署来做那里面的 Jupyter notebook。 安装 Elasticsearch 及 Kibana 如果你还没有安装好自己的 Elasti…...

【知识点】 C++ 构造函数 参数类型为右值引用的模板函数
C 构造函数是一种特殊的成员函数,用于初始化类对象。C 中的构造函数主要分为以下几种类型: 默认构造函数(Default Constructor)参数化构造函数(Parameterized Constructor)拷贝构造函数(Copy C…...
华为云服务器-云容器引擎 CCE环境构建及项目部署
1、切换地区 2、搜索云容器引擎 CCE 3、购买集群 4、创建容器节点 通过漫长的等待(五分钟左右),由创建中变为运行中,则表明容器已经搭建成功 购买成功后,返回容器控制台界面 5、节点容器管理 6、创建redis工作负载 7、创建mysql工作负载 8、…...
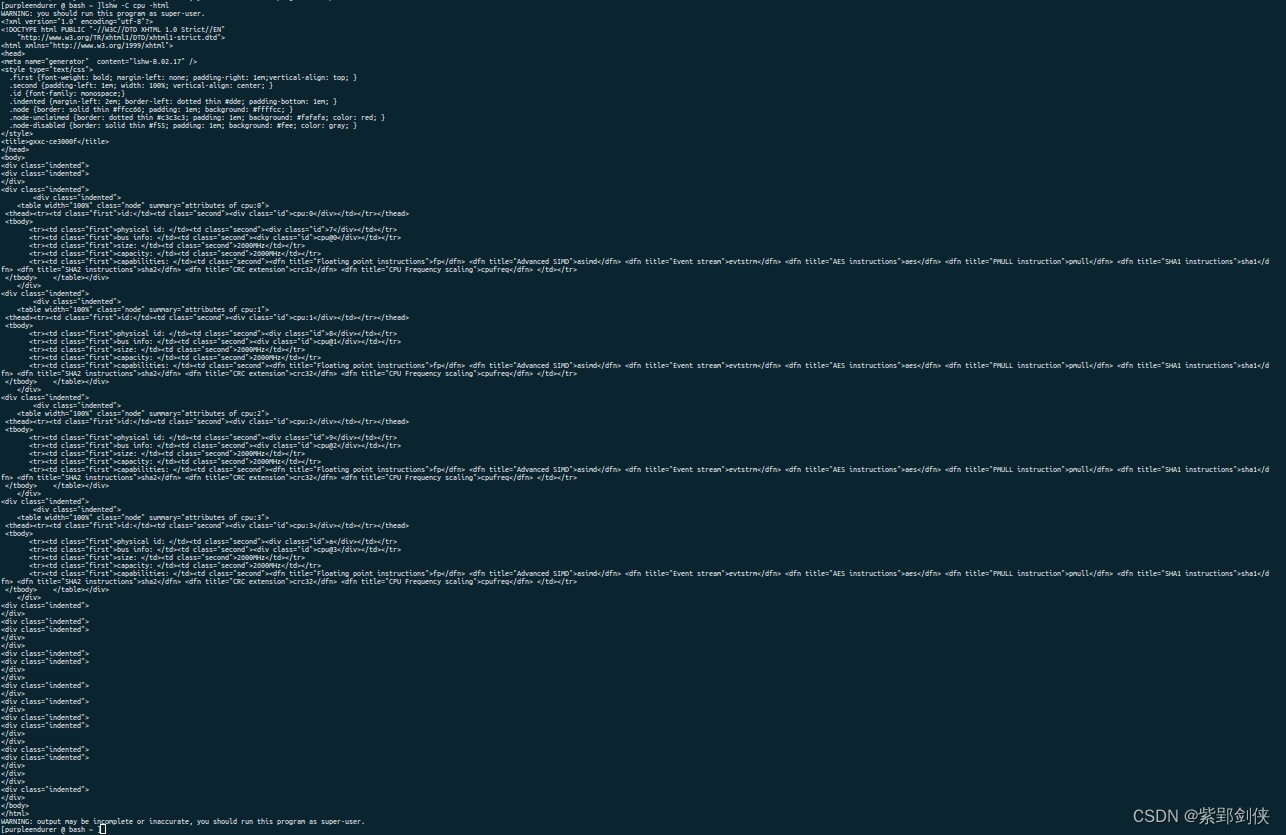
Linux shell编程学习笔记57:lshw命令 获取cpu设备信息
0 前言 在Linux中,获取cpu信息的命令很多,除了我们已经研究的 cat /proc/cpuinfo、lscpu、nproc、hwinfo --cpu 命令,还有 lshw命令。 1 lshw命令的功能 lshw命令源自英文list hardware,即列出系统的硬件信息,这些硬…...

连山露【诗词】
连山露 雾隐黄山路,十步一松树。 树上惊松鼠,松子衔木屋。 松子青嫩芽,尖尖头探出。 卷挂白露珠,装映黄山雾。...

【Qt】Frame和Widget的区别
1. 这两个伙计有啥区别? 2. 区别 2.1 Frame继承自Widget,多了一些专有的功能 Frame Widget 2.2 Frame可以设置边框...

Python爬虫实战:从入门到精通
网络爬虫,又称为网络蜘蛛或爬虫,是一种自动浏览网页的程序,用于从互联网上收集信息。Python由于其简洁的语法和强大的库支持,成为开发网络爬虫的首选语言。 环境准备 Python安装 必要的库:requests, BeautifulSoup, Sc…...

堆算法详解
目录 堆 二叉堆的实现 二叉堆的插入 二叉堆取出堆顶 (extract/delete max) 优先对列 (priority queue) 堆的实现 语言中堆的实现 leadcode 题目堆应用 堆 堆是一种高效维护集合中最大或最小元素的数据结构。 大根堆:根节点最大的堆…...

6.6SSH的运用
ssh远程管理 ssh是一种安全通道协议,用来实现字符界面的远程登录。远程复制,远程文本传输。 ssh对通信双方的数据进行了加密 用户名和密码登录 密钥对认证方式(可以实现免密登录) ssh 22 网络层 传输层 数据传输的过程中是加密的 …...
MySQL-备份(三)
备份作用:保证数据的安全和完整。 一 备份类别 类别物理备份 xtrabackup逻辑备份mysqldump对象数据库物理文件数据库对象(如用户、表、存储过程等)可移植性差,不能恢复到不同版本mysql对象级备份,可移植性强占用空间占…...

结构体(1)<C语言>
导言 结构体是C语言中的一种自定义类型,它的值(成员变量)可以是多个,且这些值可以为不同类型,这也是和数组的主要区别,下面将介绍它的一些基本用法,包括:结构体的创建、结构体变量的…...

HW面试应急响应之场景题
(1)dns 报警就一定是感染了吗?怎么处理? 不一定。 引起dns报警的情况有:恶意软件感染,域名劫持,DNS欺骗,DDoS攻击等。 处理方法: 1、分析报警,查看报警类型、源IP地址、目标域名等…...
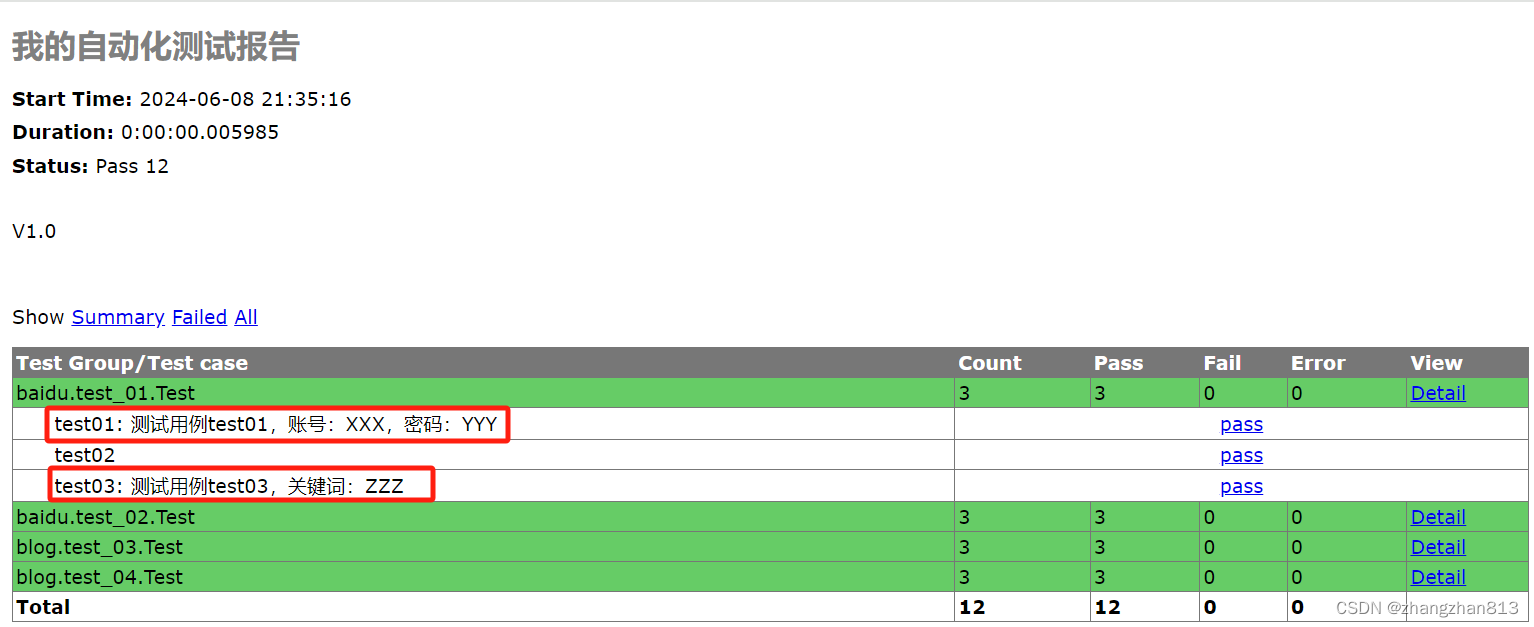
30-unittest生成测试报告(HTMLTestRunner插件)
批量执行完测试用例后,为了更好的展示测试报告,最好是生成HTML格式的。本文使用第三方HTMLTestRunner插件生成测试报告。 一、导入HTMLTestRunner模块 这个模块下载不能通过pip安装,只能下载后手动导入,下载地址是:ht…...
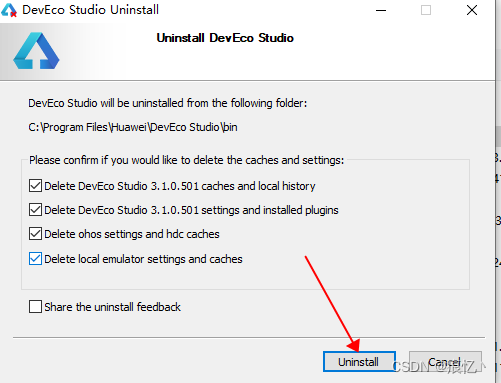
鸿蒙北向开发 IDE DevEco Studio 3.1 傻瓜式安装闭坑指南
首先下载 安装IDE 本体程序 DevEco Studio 下载链接 当前最新版本是3.1.1,下载windows版本的 下载下来后是一个压缩包, 解压解锁包后会出现一个exe安装程序 双击运行安装程序 一路 next ( 这里涉及安装文件目录,我因为C盘够大所以全部默认了,各位根据自己情况选择自己的文件…...

Oracle数据库面试题-9
81. 请解释Oracle数据库中的林业数据处理方法。 Oracle数据库中的林业数据处理 在Oracle数据库中处理林业数据涉及到存储、管理、分析和可视化与林业相关的数据。以下是林业数据处理的一些关键方面以及如何使用Oracle数据库进行示例性的SQL说明: 数据库设计&#…...
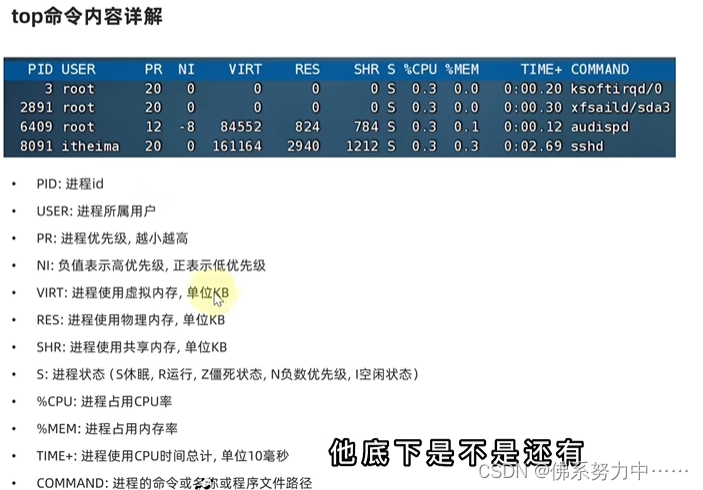
跟着小白学linux的基础命令
小白学习记录: 前情提要:Linux命令基础格式!查看 lsLinux 的7种文件类型及各颜色代表含义 进入指定目录 cd查看当前工作目录 pwd创建一个新的目录(文件夹) mkdir创建文件 touch查看文件内容 cat、more操作文件、文件夹- 复制 cp- 移动 mv- 删…...

2024-06-08 Unity 编辑器开发之编辑器拓展9 —— EditorUtility
文章目录 1 准备工作2 提示窗口2.1 双键窗口2.2 三键窗口2.3 进度条窗口 3 文件面板3.1 存储文件3.2 选择文件夹3.3 打开文件3.4 打开文件夹 4 其他内容4.1 压缩纹理4.2 查找对象依赖项 1 准备工作 创建脚本 “Lesson38Window.cs” 脚本,并将其放在 Editor 文件…...
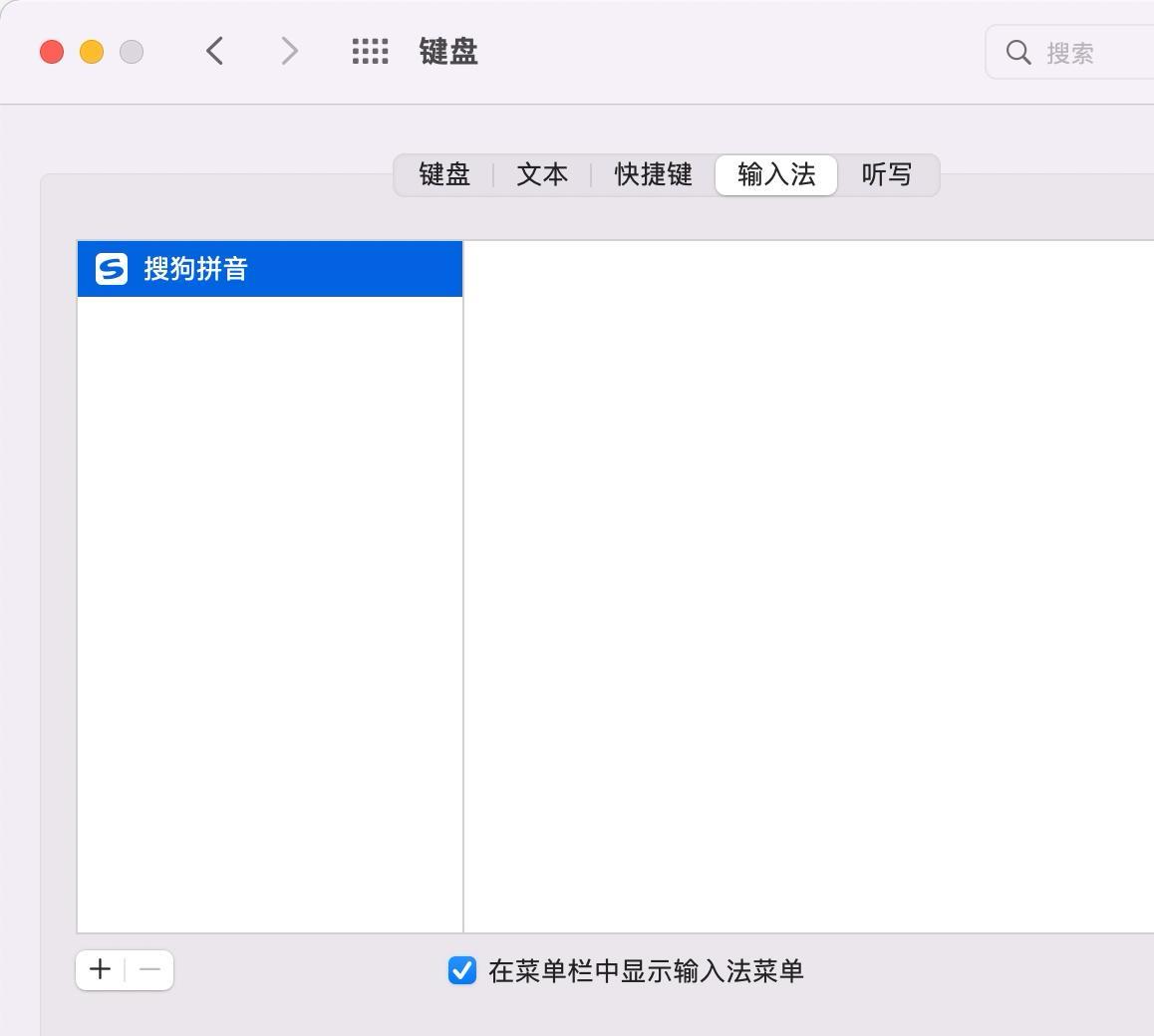
Mac下删除系统自带输入法ABC,正解!
一、背景说明 MacOS 在 14.2 以下的系统存在中文输入法 BUG,会造成系统卡顿,出现彩虹圆圈。如果为了解决这个问题,有两种方法: 升级到最新的 14.5 系统使用第三方输入法 在使用第三方输入法的时候,会发现系统自带的 …...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
